紧急加单情况下柔性作业车间调度研究

王 晋,郭丰赫,汪 鼎,翟鹏飞

(西安航空学院 机械工程学院， 西安 710077)

随着经济和信息技术的快速发展，制造企业为了改善生产效率、提高自身的竞争力，使得信息的共享与资源合理化分配运用越来越广泛，企业也越来越关注对车间中复杂多变的生产活动进行高效调度[1]。车间在生产过程中，会面临各种各样的紧急情况，如机器故障、来料延迟、紧急加单等[2]，若仍采取传统的预调度处理方法，无法精确、高效地处理紧急情况，难以保证生产效率。车间生产调度问题是制造领域研究的基础问题[3]，其主要任务是在有限的制造资源条件下，确定工件在机器上的加工顺序和加工时间，以优化特定的目标。而柔性作业车间调度问题突破了机器和工艺路线的约束[4]，相比传统的流水作业车间调度更接近实际生产[5]。在实际的生产过程中，出现紧急情况概率较大[6]，本文主要以最普遍的紧急加单情况下的柔性作业车间调度问题进行研究。

针对车间调度柔性化、动态化的发展趋势，本文对柔性作业车间动态调度问题进行了研究。首先构建了基于大数据云计算下的柔性作业车间动态调度的体系构架，使初始调度性能在受紧急加单情况的影响下不产生较大的下滑，即维持初始调度的稳定性，同时在此基础上提高其快速性；其次设计基于博弈论的柔性作业车间动态调度优化方法，给出动态调度实施的具体策略；最后通过MATLAB仿真实验结果验证该调度方法，说明了该调度方法能够很好地解决柔性作业车间动态调度问题。

1 基于大数据云计算下柔性作业车间动态调度体系构架

通过Google提出的Map/Reduce编程模型,其中Reduce作业调度是指:在 Map和 Reduce两个阶段，如何把大量作业有效地分配到相应的计算资源上，最大限度地满足用户需求和时间合理分配等要求[7]。将其运用到生产车间中，建立基于大数据云计算下柔性作业车间动态调度体系构架，如图1所示。

在体系构架中，先将总订单上传，通过感知系统，得知总订单及所有车间生产信息，并上传至云平台，构建柔性车间信息数据仓库(如Teradata AsterData、 EMC GreenPlum、 HP Vertica 等)，同时针对单个车间建立数据集市(如QlikView、 Tableau 、Style Intelligence等)，通过前端展现工具(如BDP、大数据魔镜、FineBI等)分级分析、处理数据以预测工件准备和运输时间、各个车间的生产能力(可工作机器与工人数量等)，并通过云计算根据预测结果将总订单分割分配到各个车间。车间对于这些紧急加单，以基于博弈论的柔性作业车间动态调度优化模型对其进行重调度，进而达到优化柔性作业车间生产的目的。利用大数据下云计算可达到实时获得生产任务信息的效果，其中车间生产数据云计算和生产任务关系，如图2所示。

基于各个车间的情况(可工作机器与工人)的实时数据，切分成适当的子任务(pieces)，Map Reduce Library启动复制操作，将用户信息复制到各个工作车间(a cluster of shops)上，通过云计算(master)过滤子任务，选择适当的车间(worker)，并将子任务(map任务或者是reduce任务)分配给这些车间进行预览，信息无误后车间开始进行子任务。

针对车间调度的动态化、柔性化趋势，本文提出了基于大数据的云计算下柔性作业车间动态调度的框架。云计算环境下车间用基于博弈论的方法将最优的工序分配到最优的机器上，直到所有的工序分配完成，并得到加工反馈。基于大数据的云计算，利用其有能力提供灵活动态的IT(Information Technology)基础设施，在生产过程中，当有紧急加单情况出现时，通过事件驱动动态调度策略进行重调度。

2 动态博弈模型

在基于大数据云计算下柔性作业车间动态调度体系构架的基础上，紧急加单作为一种常见的不确定因素，引起了人们广泛的研究兴趣，为了提高紧急加单情况下工件的生产效率和生产质量，设计一种基于非合作博弈论下的优化方法，目的是优化受影响下工序加工的稳定性和快速性。

博弈三要素:收益I(局中人)；G(策略) ；目标U(收益)；

车间内共有M(M≥2)台机器。

假设某一时刻：

在零时刻，所有的工件都可被加工；工序一旦进行不能中断；所有机器在零时刻均处于空闲状态；所有工件按一定顺序加工；每个工件有多道工序；在任何时刻一个工序只能在一台机器加工；不考虑工件的准备与运输时间；每台机器只能加工一道工序。

运行方式：在车间动态调度环境中，使用物联网控制，通过无线射频技术可得知每个机器的状态，并投入所需加工的工件。分配给多个机器处理调整并执行，在工件生产不合格时，会进行加工反馈，启动子任务的重新分配。

2.1 定义变量

变量定义如表1所示。

表1 变量定义

2.2 定义局中人

I是局中人集合。就基于紧急加单的车间作业调度问题而言,选择稳定性与快速性作为非合作动态博弈中的参与者，应满足紧急加单情况下稳定性与快速性独立做出决策并且两者互不干扰的原则。构成二人非合作博弈模型。I=(R，S)，R为稳定性，S为快速性，他们都是博弈的参与者。

2.3 策略集

在车间动态调度环境中，通过无线射频技术可得知每个机器的状态。本文将可选择的机器集作为生产的策略，车间可构成一个二人非合作博弈G= (G1，G2)，G1是R的策略集合，G2是S的策略集合，在调度中采用纯策略。采用纯策略的原因是在混合策略中，参与者是按照某种概率来选择行动，但是在柔性作业车间调度问题中，让工件以某一概率去选择可选机器进行加工仍然具有不确定性，发生重调度时总是希望以一种确定的方式采取行动，所以在调度中每个局中人必须采用纯策略。

在这种情况下，可采用多阶段博弈。假设在受紧急加单情况下影响的加工工序为N(N≥2)道，将这些工序每两道为一组分为若干组，当工序为奇数道时，末道单独成组。每组则可以为参与博弈的双方各分配一道工序，每个参与者的策略集就是工件可能选择的加工机器。参与者为自己的工序选择策略(加工机器)的原则是使各自的性能达到最优，同时Nash均衡目的使二人博弈达到均衡，可构成一个二次博弈矩阵。

2.4 收益函数

调度目标是在紧急加单情况下使稳定性与快速性达到Nash均衡点，实现生产最优化。在该模型中，快速性作为R的利益函数，稳定性作为S的利益函数，并令U作为参与者的利益函数集合。由于该模型是双人博弈模型，故参与者的利益可以写成q1*q2的效益矩阵。该矩阵的列作为R的策略，行作为S的策略。在这里，策略指的是工件所选择的加工机器(当受影响的工件≥2成立)。

效益矩阵q1*q2表示如下：

3 两道原有工序受影响下的Nash均衡求解

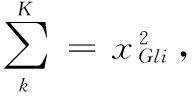
如果受紧急加单影响的工序只有两个，则可以为参与博弈的双方各分配一个工序，每个参与者的策略集就是工序可能选择的加工机器集，参与者为自己的工序选择加工机器的原则是使各自的性能达到最优。在快速性和稳定性的博弈中，Nash 均衡可以使得这两个指标达到均衡。在本文所讨论的问题中，快速性和稳定性越小，对预调度的影响越小，调度性能越好。因此本模型的Nash均衡的定义为：

本文给出了Nash均衡的存在条件，但博弈论中亟待解决的问题是在离散条件下如何寻找Nash均衡，且大部分方法都是寻找混合策略的Nash均衡解，对生产有一定的不确定性影响。因此本文针对二人博弈的特点，提出基于利益矩阵的Nash均衡搜索算法，寻找纯策略Nash均衡解。该算法描述如下所示：

算法步骤：

1) 机器因为预先的工作安排和紧急加单情况下工作时间延长的所受的影响；

2) 为每个操作采取可选择的机器设备S1和S2，计算两个集合的基数并用q1和q2表达出来；

3) 依据从S1，S2中获得的每个策略集，建立q1*q2规模的矩阵结果；

5) 记录纳什均衡解决方案。最后i=i+1；

6) 输出结果。

4 多道原有工序受影响下的Nash均衡求解

当受紧急加单情况下影响的工序大于两个时，参与者的策略数量将大幅增加，给求解带来巨大困难，因此本文的模型无法直接运用。故本文将通过多阶段博弈来解决空间策略庞大的问题，中心思想是将这些工序每两道为一组分为若干组，当工序为奇数道时，末道单独成组。每组则可以为参与博弈的双方各分配一道工序，然后构造每组的动态博弈模型，称为博弈的一个阶段。如果有n组工序，就有n个阶段的博弈。上一阶段博弈结果的输出作为下一阶段的博弈的输入。最终得出纯策略Nash均衡解。该算法描述如下：

算法步骤：

1) 确定受紧急加单影响下的工件；

2) 将操作划分为n(n=(N/2))组，其中每组包含两个操作，除了最后一个组包含一个或两个操作(N为受影响的工件)；

3)i=1；

4) 得出Nash均衡解并更新调度；

5)i=i+1;

6) 如果第i组不是最后一个然后转到步骤4)；否则转到步骤7)；

7) 当最后一组只有一个操作，采用穷举法。当最后一组有两个操作得出纳什均衡解并更新调度；

8) 输出结果。

如果只有一个工序受到影响时,博弈的两个参与者不得不选择相同的策略，因此参与者已经不存在Nash博弈的过程。在此情况下，只能采用穷举法，即对每一个可选的加工机器加以考察，如果存在1台机器加工该工序后整个调度的快速性和稳定性比选择其他机器要小，则该加工机器为最优选。

5 应用算例

一个加工系统有3个工件，4道工序。初始调度加工如表2所示。

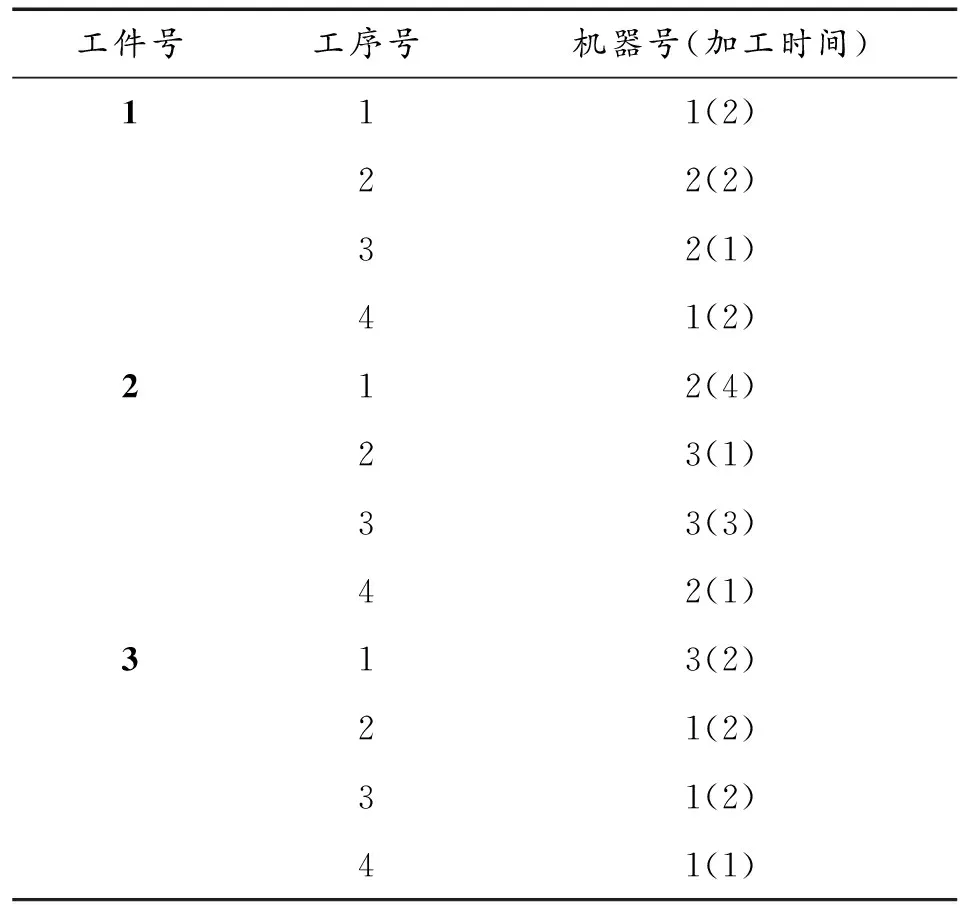
表2 初始调度加工时间

预调度算法：紧急加单作为一种常见的未知因素，虽然准确信息通常无法提前得知,但可以根据历史数据用统计学的方法了解紧急加单发生的概率，所以紧急加单的概率在一定程度上是可以预知的。在紧急加单发生概率已知的情况下可以采取措施来生成预调度。在已有的研究基础上考虑紧急加单发生的概率和插入紧急加单工件时间生成预调度。

5.1 两道工序受影响的调度结果

调度方案在执行过程中，遇到紧急加单情况，工件3的第1工序和工件2的第2道工序受到影响，需进行重调度，如表3所示。

表3 初始调度加工表

根据动态博弈模型及Nash 均衡搜索算法得到最终执行方案如图3、图4所示。

图3、图4是对2道工序受紧急加单下的调度结果和基于紧急加单概率的预调度算法结果。由图3可知基于博弈模型的重调度结果的总生产时间为10 min，图4表示使用基于机器故障概率的预调度算法所需总生产时间为14 min[2]。也就是说，在只有两道工序受影响的情况下工序间存在足够的时间空隙吸收紧急加单情况的影响，因而基于博弈模型的调度是较好的重调度方法。

5.2 四道工序受影响的调度结果

调度方案在执行过程中，遇到紧急加单情况，工件2的第1工序，工件1的第2道工序，工件的第3工序和工件2的第4道工序受到影响，需进行重调度，如表4所示。

表4 初始调度加工表

图5、图6是对4道工序受紧急加单的调度结果和基于紧急加单概率的预调度算法结果的比较。由图5可知基于博弈模型的重调度结果的总生产时间为12 min，图6表示使用基于机器故障概率的预调度算法所需总生产时间为14 min[2]。也就是说，在多道工序受影响的情况下工序经过基于调度模型的重调度，从而利用时间空隙来吸收紧急加单的影响，与预调度算法相比较，基于博弈模型的调度是较好的重调度方法。

6 结论

本文针对柔性作业车间动态调度问题，建立了基于大数据云计算下柔性作业车间动态调度体系构架和策略，并采用博弈论的方法对柔性作业车间动态调度问题进行了建模。为验证算法的有效性，将上述算法进行MATLAB仿真实验，通过求解动态调度模型的纯策略Nash均衡解，得到了柔性作业车间动态调度的优化结果。结果表明：与其他优化调度方法相比，本文算法在解决柔性作业车间紧急加单情况下动态调度问题时，具有稳定性强，速度快，效率高等优点。

：

[1] ZHANG Y,WANG J,LIU S,et al.Game theory based real-time shop floor scheduling strategy and method for cloud manufacturing[J].International Journal of Intelligent Systems,2016(10)：71-74.

[2] 何伟.机器故障下柔性Job Shop调度研究[D].重庆：重庆大学,2012.

[3] 杨武，崔英志，胡爽.基于连续多媒体的磁盘调度[J].四川兵工学报，2010,31(7)：85.

[4] 余琦玮,蒋海青.柔性作业车间动态调度问题研究[J].科技与企业,2013(19):36-37.

[5] 杨琴,周国华,林晶晶,等.基于DBR理论的柔性流水车间动态调度[J].控制与决策,2011,26(7):1109-1112.

[6] 李开红,肖辉，李横，等.基于匈牙利算法的战时运油车前送油料调度优化模型研究[J].四川兵工学报，2015(6):61-65.

[7] 梁静,许波,葛宇.基于改进蛙跳策略的Map-Reduce作业调度算法[J].计算机应用研究,2013,30(7):1999-2002.