超磁致伸缩驱动器偏转弹头的控制模型

张 冲，周春桂，李明星，刘亚昆，陈 杰

(中北大学 机电工程学院， 太原 030051)

弹头偏转控制是一种新颖控制方式，国内在动力学[1-4]、控制机构[3-8]等多个方面对其进行了研究。相继提出了电机驱动、液压泵驱动和压电材料[9]、记忆合金[7]、电(磁)流变液、磁致伸缩材料[10]等新型材料驱动方式。魏方海、王志军[9]对压电驱动原理进行了介绍，并建立了驱动器力学模型。王建，樊少军[7]对利用镍钛合金丝的记忆特性控制弹头的偏转进行了机理研究，实现了DSP的控制设计。冷松劲,刘艳菊[10]设计了一种基于智能材料驱动器的头部能够偏转的弹药，但并未对其内部驱动原理和控制模型分析。

现有研究的偏转控制器大多结构复杂、驱动控制不便，采用超磁致伸缩材料制作的偏转驱动器克服了这些缺点。超磁致伸缩材料(GMM)具有磁致伸缩效应，即材料的磁化状态发生改变时，材料应变发生显著变化。采用这种材料制作的驱动器，具有输出力大，位移分辨力高，位移范围大、设计相对简单、反应速度快等特点，相对其他驱动器具有明显优势。

针对控制弹头偏转的超磁致伸缩驱动器，主要任务是建立驱动器的机构动力学模型和磁滞模型。用拉格朗日动力学方程建立驱动器机构动力学模型，用J-A模型建立材料的磁滞模型，J-A模型基于磁畴理论，能够反映材料的内在物理机制。

本文在建立数学模型的基础上通过数值仿真对驱动器驱动过程中电流-磁化强度，电流-偏转角关系进行分析。

1 驱动器机构动力学模型

1.1 驱动器原理与结构分析

采用磁致伸缩材料制作的驱动器的偏转弹整体机构如图1所示[10]。制导控制系统分为导弹制导系统和稳定控制系统两部分，磁致伸缩驱动器替代传统稳定控制系统中舵机的作用。通过可移动的头锥，围绕导弹轴上的单个多向接头枢转动，产生控制弹箭飞行路径的控制力矩。

弹箭位置信息由GPS或北斗定位系统获取，与弹箭预期轨迹比对后，生成指令传递给稳定控制系统，控制弹药鼻锥偏转。位于弹头内部的光检测器感知弹头顶端激光发射器入射角的变化，产生的电信号实时传递给弹载计算机。计算机通过接收到的信号确定当前弹鼻锥偏转角，与预期偏转角进行比对，差值信号再次传递给传递弹载计算机，进行处理后输出指令控制Terfenol-D的伸长缩短。该多回路控制，可以实现弹箭运动的实时控制。

位于弹体中的磁致伸缩驱动器具体结构如图2所示，该智能材料选用超磁致伸缩材料Terfenol-D。预紧螺钉为超磁致伸缩材料提供一定的预压力，一方面可以增大磁场对超磁致伸缩系数和磁致伸缩系数的灵敏度。另一方面GMM的抗拉强度(大约28 MPa)远小于抗压强度(大约700 MPa)，预压力的添加可以增强材料的抗拉能力[11]。GMM在电流产生的磁场作用下伸长，经放大装置放大后由输出端10输出。

1.2 驱动器动力学模型

对驱动器进行机构动力学建模。超磁致伸缩驱动器中的放大机构采用硬铝合金7075制作，可看作理想刚体，各处应变为零。为简化系统的动力学特性运算，将弹头偏转过程中约束力经放大机构等效为驱动器预紧力Fd。将驱动器的预紧螺钉、输出杆等效为弹簧-阻尼系统；将Terfenol-D棒视为粘弹性连续系统，对其进行动力学建模。依据机构动力学将超磁致伸缩驱动器分为两部分：第一部分是超磁致伸缩棒受磁场磁化，在轴向产生应变的主应变部分；第二部分是驱动器的负载产生的应变部分。动力学系统的运动过程由外部磁场作为激励源，通过控制磁致伸缩棒的伸长量引起整个系统受迫振动，系统动力学模型如图3所示。

假设Terfenol-D棒一端固定位移为零，设N、ls、I分别为激励线圈的匝数、长度和输入电流；EH、lr、d、Ar、ρ、CD分别为GMM棒的弹性模量、长度、直径、横截面积、质量密度、内部阻尼系数，Kr、Cr、Mr分别为GMM棒的等效刚度系数、等效阻尼系数和等效质量；Kl、Cl、Ml为分别为负载的等效刚度系数、等效阻尼系数和等效质量；建立拉格朗日动力学模型，分别求GMM棒和负载的动能和势能。

Terfenol-D棒产生的总应变由外部应力引起的弹性应变和磁场的磁致伸缩应变两部分构成，可由线性压磁方程[12-14]给出：

ε=σ/EH+dH

(1)

B=dσ+μH

(2)

式中，ε为Terfenol-D棒沿长度方向的总应变；σ为Terfenol-D棒所受的应力;d为Terfenol-D棒的磁致伸缩系数；H为磁场强度；B为磁感应强度；μ为磁导率。

当考虑磁场的磁滞非线性时，式(1)可表示为：

ε=σ/EH+λ

(3)

应用微元法，GMM棒的动能等于各个微元d的动能之和，动能表示为：

(4)

包括负载在内的系统总动能为：

(5)

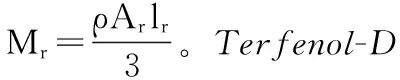
(6)

(7)

系统拉格朗日方程为L=T-V,系统的耗散函数D为：

(8)

将拉格朗日函数L和耗散函数D代入拉格朗日方程：

(9)

得：

(10)

进行拉普拉斯变换，有：

(11)

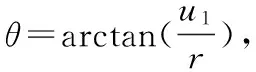
(12)

2 Terfenol-D棒的Jiles-Atherton磁滞模型

基于磁畴理论的J-A模型，建立Terfenol-D棒外磁场H和磁化强度M的关系。其主要方程表达式如下：

(13)

M=Mirr+Mrev

(14)

Mrev=c(Man-Mirr)

(15)

(16)

(17)

(18)

由式(12)、式(17)得超磁致伸缩驱动偏转弹的数学模型如下：

(19)

模型中参数需要通过参数辨识确定，常用的有最小二乘法、神经网络算法和遗传算法，仿真中采用的参数如表1中所示。

表1 Jiles-Atheron模型参数值

Terfenol-D棒λs=1 005×10-6，d=12.7 mm,lr=115 mm;激励线圈的N=1 200；负载的Ml=0.5 kg，密度ρ=9 250 kg/m3，EH=3×1010N/m2。确定Mr=0.045 kg，Cr=3.305×103Ns/m,Kr=3.305×107N/m通过测得制动器的机械共振频率，得到,Cl=1×103Ns/m,Kl=5.67×107N/m。

3 数值仿真

根据各部分建立的数学模型，在Matlab/Simulink平台中搭建超磁致伸缩驱动器的弹头偏转控制仿真模型，对驱动器电流-磁化强度，电流-偏转角关系进行分析，超磁致伸缩驱动弹头偏转的控制仿真模型方框图如图4所示。驱动器输入电流信号为3sin(2πt)，频率为1 Hz，仿真步长为1.25个周期。

驱动器输入电流信号与GMM棒磁化强度间的关系如图5所示，从图中可以看出GMM棒在零时刻磁化强度为零，经过1/4个周期完成初始磁化，达到当前输入下的最大磁化强度。由于磁化强度不仅依赖于外磁场强度，还依赖于原磁化强度，所以磁化强度变化总是滞后于外磁场强度的变化，产生磁滞回线。

驱动器输入电流I与偏转角θ的关系如图6所示，初始状态下，偏转角随着输入电流的增大而增大，达到最大偏转角。然后偏转角随电流的变化周期性变化，具有很强的非线性。

驱动器输入电流I和输出偏转角随时间的变化如图7所示，从图中可以看出0～0.25 s是初始磁化阶段，在0.25～1.25 s时间段，偏转角的变化频率是正弦信号的2倍。

4 结论

1) 如图6所示的输入电流I与偏转角θ的曲线中，输入电流在上升和下降时都存在近似线性段，整个系统在该范围内近似为线性系统，只需要简单的PID控制算法便可以控制系统性能指标。

2) 当要求偏转角幅度在零到最大偏转角之间任意变换时，由图6可知，输入电流I与偏转角θ间非线性强；由图7可知，偏转角θ随时间的变化频率是输入电流I随时间的变化频率的2倍。针对此类问题大多采用前馈控制结合PID控制或者可调参数PID控制对系统进行校正，从而控制系统性能指标。

：

[1] 徐永杰,王志军,吴国东,等.弹头可偏转火箭弹外弹道特性研究[J].弹箭与制导学报,2016,36(1):121-124.

[2] 王辚,范文涛,高原.偏转弹头导弹气动特性研究[J].弹箭与制导学报,2014,34(2):123-126.

[3] 刘宣，闻泉，王雨时，等.弹头外形对非零攻角亚音速旋转弹丸气动特性的影响[J].兵器装备工程学报，2016(9):5-10.

[4] 梁毅辰.偏转弹头导弹气动方案设计研究[J].兵器装备工程学报，2016(7):47-50.

[5] 胡寒栋,谷良贤,梁毅辰,等.锥齿轮推杆式弹头偏转机构的设计与仿真[J].机械科学与技术,2015,34(7):1127-1130.

[6] 王明,谷良贤,高原.斜盘式偏转机构方案仿真研究[J].计算机仿真,2008,25(10):23-26.

[7] 王建,樊少军,刁云鹏,等.战术导弹智能偏转弹头控制系统研究[J].科学技术与工程,2009,9(17):5123-5127.

[8] 谷良贤,白壬潮,孙晓峰,等.两种弹头偏转机构的适用性研究[J].应用力学学报,2014(05):678-684.

[9] 魏方海,王志军,尹建平.一种新型压电驱动器技术的研究及应用[J].弹箭与制导学报,2006,26(1):137-139.

[10]冷松劲,刘艳菊,黄剑阳.基于智能材料驱动器的头部可以偏转的弹药：中国，103105103[P].2013-05-15.

[11]LACHEISSERIE E D T D.Magnetostriction:Theory and applicationsof magnetoelasticity[J].Natre,1993.

[12]CLARK A E.Magnetostrictive Rare Earth-Fe2,Compounds[M]//Power Sonic and Ultrasonic Transducers Design.Springer Berlin Heidelberg,1988:43-99.

[13]FAIDLEY L E,LUND B J,FLATAU A B,et al.Terfenol-D elasto-magnetic properties under varied operating conditions using.[J].Proceedings of SPIE-The International Society for Optical Engineering,1998.

[14]CALKINS F T,SMITH R C,FLATEAU A B.An energy-based hysteresis model for magnetostrictive transducers[J].IEEE Transactions on Magnetics,2002,36(2):429-439.

[15]徐彭有.超磁致伸缩驱动器精密位移驱动控制研究[D].上海：上海交通大学,2010.

[16]DAPINO M J,SMITH R C,FLATAU A B.Structural magnetic strain model for magnetostrictive transducers[J].Magnetics IEEE Transactions on,1999,36(3):545-556.