两台等级平行机上部分处理时间已知的半在线调度∗
2021-08-08杜豫菲
杜豫菲
(云南大学数学与统计学院 昆明650000)
1 引言
“半在线”是一种所谓特殊的“在线”。一般地,“在线”调度是指工件一个个到达,一旦到达就必须安排加工,而且工件一旦分给某台机器处理就不允许改变。而半在线是在第一个工件到达前就预先知道工件的部分信息,比如工件的最大处理时间、任务的总处理时间等[1]。设I为某调度问题的一个实例,对于一个在线或者半在线算法A,CA(I)记为算法A对实例I的调度时间,Copt(I)则指算法对相应问题离线情况的最优目标值,我们把CA(I)/Copt(I)称为算法A的竞争比,将其记为R[2~3]。竞争比是刻画一个算法优劣的重要参考依据。而等级调度(GoS)在服务行业中较为常见。等级调度将工件划分为不同等级,对不同等级的工件进行不同的处理。企业通过等级调度,为不同需求或等级的客户提供差异化服务,不仅可以提高自身的服务效率,也可以提升客户消费体验[4]。现实生活中,高速收费站车道被划分为ETC车道,绿色通道和普通车道就是进行等级调度的一个实例。接下来,我们将分别介绍在半在线调度领域和等级调度领域的一些成果。为了描述方便,本文用三参数表示法来表示问题,如,表示在两台机器的工作环境下,si为半在线问题提前已知的信息,目标函数是使总处理时间尽可能小。
关于半在线调度问题的研究十分丰富。在1997年,Kellerer和Kotov等[5]考虑提前已知所有工件的总处理时间的半在线问题,得到已知总处理时间在任何算法下竞争比都大于等于,并得到相应的最优算法竞争比R可到达。Azar和Re⁃gev[6]于2001年在中指出,一个已知最优处理时间的半在线问题可以等价于一个背包数目确定,背包具有拉升系数的bin-stretching问题。bin-stretch⁃ing问题在两台机器下的拉升系数为。更进一步,对于两台或者更多的机器,任何确定的算法的拉升系数大于等于[6]。He和Zhang[7]在1999年证明了两台平行机工作环境时最大处理时间已知的情况,该情况下最优的半在线算法为PLS算法,其竞争比与上两个情况相同,也是。Zhang和Ye[8]在1999年证明了当最后一个工件处理时间最大的情况,算法竞争比可以到达当工件的处理时间是的等比数列时,竞争比一定不超过2k[9]。同样地,一些已知信息相互搭配的半在线调度问题也已被研究。例如:在2002年Tan和He证明了总处理时间已知和工件最大处理时间已知情况下,有SM算法使得竞争比为;工件集合是一个不递增的序列,且已知总处理时间在任何算法下的竞争比R大于等于,并有最优的算法——SD算法竞争比为;以上这两种组合情况Tan和He[10]给出了具体的证明。
在等级调度领域,我们从离线、在线和半在线三个方面来介绍,由于是NP-难问题,我们关注近似算法来解决这一类问题[11]。离线情况下,Hwang等[12]在2004年第一次研究了多台平行机工作环境下的等级调度问题,并提出了一种近似算法,该算法在两台机器时可以使竞争比不超过,当机器数大于两台时,竞争比R可达2−1/(m−1),其中m是机器数。对于在线的问题,Bar-Noy等[13]考虑了一个相似的模型,并给出该模型的一个近似算法,该算法竞争比为e+1。半在线的等级调度问题也有大量的研究。例如:2015年Chen等[15]研究了等级调度和提前已知部分信息组合的情况;当提前已知最优处理时间和工件最长处理时间,无论是在的竞争比都分别是
在前人的研究基础上,本文主要讨论了等级调度情况下的两台平行机上的三个半在线调度问题。该问题模型为工作环境为处理速度相同的两台平行机M1和M2,工件被划分为两个等级gj=1和gj=2。机器M1只能处理等级gj=1的工件,机器M2即能处理等级gj=1的工件,也能处理等级gj=2的工件。三个半在线问题都在等级gj=1工件总处理时间已知的前提下,各自分别还知道:1)算法最优的处理时间,即Copt已知;2)工件中最大的处理时间,即pmax已知;3)算法最优的处理时间和工件中最大的处理时间,即Copt,pmax同时已知。目标是总处理时间尽可能小。
2 准备工作
模型中有两台平行机M1和M2,两台机器处理速度相同。机器M1只能处理等级gj=1的工件,机器M2能处理等级gj=1和gj=2的工件。
处理思路:等级gj=1的工件只能在第一台机器M1上处理,我们已知等级gj=1工件总处理时间,故在第一台机器M1上预留出等级gj=1的工件的总处理时间,这样无论等级gj=1的工件何时到达,都不影响机器M1对它的处理,也平衡了资源的利用。在后两个模型中,我们默认最大处理时间的工件为等级gj=2的工件,因为等级gj=1的工件自然分配到第一台机器M1上,机器M1也为其留出了处理时间,所有等级gj=1的工件有多少或者有多大及到来顺序对问题本身没有实质的影响。故本文只考虑最大处理时间的等级gj=2的情况。
文章讨论的三种半在线问题均在等级gj=1的工件的总处理时间已知的前提下进行,其中,每个半在线问题分别还知道的信息:1)最优处理时间,即已知Copt;2)工件的最大处理时间,即已知pmax;3)以上两种搭配组合的情况,即已知Copt和pmax。
Mi:当前状态下第i台机器的负载;
T1:等级gj=1的工件的处理时间之和;
Sj:当第j项工件被处理时,第二台机器上等级gj=2的工件的总处理时间;
pmax:工件中最大的处理时间;:工件中处理时间最大的第一个工件;工件中等级gj=2的最后一个工件的处理时间。
以下算法在后面的算法中应用到。
算法LS[17]
步骤1若gj=1,则将该工件分配给M1;否则,执行第二步;
步骤2如果Sj−1+T1≤M2,则将工件pj分配给M1;否则分配给M2;
步骤3若j 定理3.1问题的竞争比R大于等于 证明 假设等级gi=1的总处理时间T1=1,Copt=3。默认将等级gi=1的工件安排到机器M1上。第一个工件集为;第二个工件集为以上两个工件集都能通过离线算法达到最优,且最优处理时间为3。假设一个确定算法接受到了两个工件的处理时间为1。 1)第一个工件默认分配到机器M1,第二个工件分配到机器M2,第三个工件为(3,2)时,无论将其分配到任何一台机器,该算法的竞争比都是 2)将前两个工件(1,1)(1,2)都安排到机器M1上,剩下的两个工件可以安排到同一台机器或者不同的机器,但无论哪种情况下算法的竞争比为 我们将bin-stretching问题中的算法[6]进行简单的推广,并证明该算法的竞争比小于等于为了方便叙述,称该算法为OT算法。 算法1 OT 步骤1如果gj=1,将该工件分配给机器 M1; 步骤2如果T1=Copt,将所有的gj=2的工件安排给机器M2,结束;否则执行步骤3; 步骤3如果Sj−1+T1≥Copt,将j及之后所有gj=2的工件分配给机器M2; 定理3.2算法OT的竞争比小于等于 证明 分以下两种情况进行讨论: 1)如果T1=Copt,则最优。 2)如果T1 这一部分,我们讨论等级gj=1的总处理时间和工件中最大处理时间已知的半在线问题。当最大处理时间的工件的等级gj=1时,可以将该问题考虑为只知道等级gj=1的总处理时间的半在线问题,其竞争比R大于等于故,以下只考虑最大处理时间的工件等级gj=2的情况。 定理4.1问题在任何算法下的竞争比R大于等于 证明 假设pmax=2,T1=1。 1)算法将前两个工件(1,1)(1,2)分配到两台机器上,工件(2,2)无论分配到哪里台机器上,竞争比R都是 2)算法是将前两个工件(1,1)(1,2),安排在机器M1上,紧接着的两个工件具有相同的处理时间2,即为工件(2,2)(2,2),无论将这两个工件安排到哪一台机器上进行处理,算法的竞争比R为 算法2 MT 步骤1若gj=1,则将该工件分配给M1;否则,执行步骤2; 步骤2若pj≠pmax或pj+Sj−1+T1≤2pmax时将pj分配给M1,接着执行步骤3;否则将pj分配给M2,接着执行步骤4; 步骤3若j 步骤4用具有服务等级的LS算法[14]进行调度;结束。 定理4.2MT算法的竞争比R小于等于 证明 我们将证明对于任何实例PLS算法的竞争比R小于等于假设pn是实例的最后一个工件,两台机器的负载分别为M1和M2。我们讨论一下几种情况。 1)M2=0,即当p0max到达时,还没有工件分配给M2。pn=pmax。 (1)若M1≤pmax,那么CPLS=pmax,此时最优。 (2)若M1>pmax,则CPLS=M1。又因为算法设计知M1<2pmax,另有因此,可得出 2)0 (1)当M2 (2)当M2≥pmax时,有即 即 3)M2>M1。在这一情况中我们把分配机器M1。M2≥pmax必然成立,否则Sn−1+T1>pmax。此时第二种情况类似,与假设M2>Sn−1+T1产生矛盾。当Sn−1+T1 (2)M2−M1≤pmax。结 合得 前两节已经对最优处理时间和最大处理时间分别已知的半在线问题进行了讨论。这一节,对以上两种已知条件组合在一起的半在线问题进行讨论。对于的半在线问题。已知信息s1的情况下的竞争比为c1,已知信息s2的情况下的竞争比为c2,则已知问题s1和s2的同时,竞争比R一定小于等于;若已知信息s1或s2在算法a的情况下的竞争比为ca,则算法a竞争比小于等于为ca[10]。由 此,半在线问题的竞争比一定大于等于 定理5.1P2|opt&max&T1|Cmax问题的竞争比大于等于 证明 假设Copt=5,pmax=3,T1=1。 1)前两个工件(1,1),(3,2)安排到机器M1上,则令之后工件为(2,2)(2,2,)(2,2),无论之后三个工件如何分配,都可以得到竞争比大于等于 2)若前两个工件没有分配到同一台机器上,即(1,1)安排给第一台机器,(3,2)安排给机器M2,则讨论以下几种情况: (1)若第三个工件安排在机器M1上,第四个工件也安排到第机器M1,则第三到最后一个工件依次 是(1,2)、(1,2)、(3,2)、(1,2)。可得竞争比R大于等于 (2)若第三个工件(1,2)依旧安排给机器M1,而第四个工件(1,2)安排给机器M2,则最后两个工件(2,2)、(2,2),同样可得竞争比大于等于 (3)若将第三个工件(1,2)安排到机器M2,之后两个工件为(3,2)、(2,2),无论之后工件怎么分配,都可使得竞争比大于等于 将SM算法[10]进行推广,得到以下算法,我们将其称之为OMT算法。 算法3OMT 步骤1若Copt=T1,则将gj=2的工件分配给M2,gj=1的工件分配给M1;结束。 步骤4当gj=1时,将工件给M1,若 步骤5当gj=1时,将工件给M1,若则pj分配给Mi,其余工件分配到另一台机器上;结束。 步骤6若p0max还没有到达,和pj分配给Mi,其余的配给令一台机器,结束。 步骤7若pj≤2Copt−T1或pj=pmax,则将其分配到M1; 步骤10若j 定理5.2P2|opt&max&T1|Cmax问题在算法OMT下的竞争比R小于等于 证明 当Copt=T1和Copt≤pmax≤2Copt时,算法最优。我们讨论以下几种情况。 (1)有工件pj满足 或 和3 P2| opt&T1 |Cmax
4 P2| max&T1 |Cmax

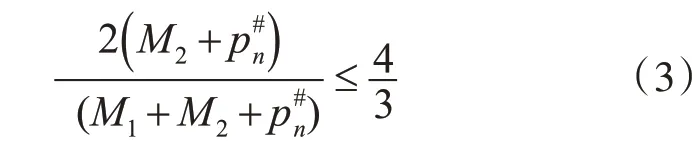

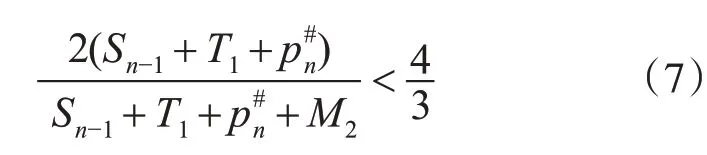
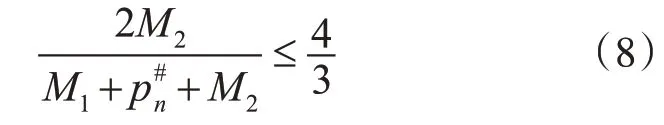
5 P2| opt&max&T1 |Cmax

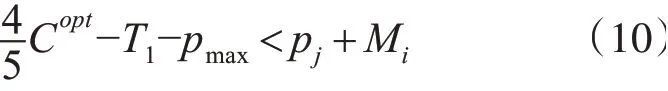
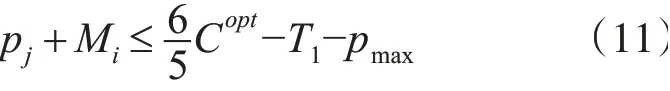

6 结语
