基于心智模型的恐怖主义袭击扩展式演化博弈分析

刘德海，柴瑞瑞,韩呈军

(1．东北财经大学管理科学与工程学院，辽宁 大连 116025； 2. 东北财经大学经济计量分析与预测研究中心，辽宁 大连 116025)

1 引言

恐怖主义是由个人、群体、组织甚至国家基于政治目的，为了在尽可能广泛的范围内制造恐怖气氛，针对政府、公众或个人使用暴力或以暴力相威胁的行动[1]。自20世纪90年代以来，恐怖分子与地区分裂势力和极端宗教势力相勾结，在我国新疆、昆明等地市策划了一系列暴恐事件，对社会的和平、安全与秩序构成了巨大威胁，造成大量无辜民众伤亡的后果。

恐怖主义问题成为当代管理科学领域重要热点问题之一。国际上有关恐怖主义问题的研究视角包括运用计量分析模型研究恐怖主义产生的社会经济根源[2-3]、运用复杂网络技术研究恐怖主义网络结构特征[4]、运用优化模型研究反恐措施的组合优化问题[5-6]。尤其是，Zhuang Jun带领的研究团队运用博弈论模型开展了政府防御措施与恐怖分子互动行为研究，具体包括反恐与防灾的投资协调问题[7]、加强安检造成拥堵问题[8]、保密与欺诈的攻防策略[9]等问题。目前，国内管理科学界对于恐怖主义问题的研究尚未得到高度重视，现有一些文献主要集中在反恐设施选址和网络的优化问题[10-12]，以及反恐中认知差异和国际合作的博弈问题[13-14]。尽管政府反恐力量针对恐怖袭击的防范对策问题属于典型的博弈问题，但是传统博弈理论基于参与者完全理性假设，包括博弈双方对于策略分布和收益结果具有“共同知识”，难以从较长时期的角度考察政府反恐力量与恐怖分子之间相互观察、适应性调整的演化问题，即所谓的“道高一尺魔高一丈”。

基于有限理性群体行为适应性分析的演化博弈理论已经广泛应用到突发事件、供应链合作等管理问题分析中[15-16]。一般来说，政府作为先行动者进行反恐防御，恐怖分子作为后行动者观察到政府行动后决定是否袭击，构成了扩展式博弈的斯塔克伯格模型[7]。但是，由于扩展式演化博弈的均衡分析需要考虑不同层次信念学习，如何在扩展式要素博弈基础进行演化分析，这是演化博弈理论上的一个难点问题[17]。本文通过引入政府与恐怖分子的“心智模型”概念，将双方行为的社会规范引入到策略分析过程中，大大简化了Cressman提出怀特流形(Wright manifold)的均衡分析过程[18-19]。本文首先构建了政府与恐怖分子的扩展式演化博弈模型，然后对比了Cressman的怀特流形均衡解与心智模型均衡解的差异，最后通过新疆墨玉县6.28暴恐事件的案例，进行了数值分析。

2 恐怖袭击扩展式演化博弈模型

2.1 要素博弈模型

政府反恐力量与恐怖分子之间的策略式要素博弈模型如表1所示。政府的可行策略集合S1={防御，不防御}，恐怖分子的可行策略S2={袭击，不袭击}。其中，恐怖分子发动的爆炸、纵火、投毒等袭击行动，都是早有预谋甚至经过严密策划，在实施过程中付出的成本记为c2。为了阻止恐怖分子的袭击，政府针对防御目标采取相应的防范和应对措施，需要支出的防御费用记为c1。恐怖分子在反恐意识较为薄弱、疏于防范的人群密集地点(如火车站和早市等)发动袭击，往往会造成较大的暴恐袭击损失。如果针对高度警戒、防御充分的政府机关等发动袭击，则将遭受严厉打击和挫败。假设在政府采取积极防御的情况下，恐怖分子采取袭击行为不但需要付出实施袭击成本c2，而且遭到政府反恐力量的严惩f。政府成功击败恐怖分子的袭击行动，大大提高了反恐措施的威慑力，获得额外收益a。在政府不防御的情况下，恐怖分子发动袭击则一定成功。显然，此时暴恐袭击行动获得利益e将大于袭击成本c2，即e-c2>0。由于疏于防范政府遭受严重损失b，该损失值大于政府防御的成本b>c1。政府采取防御措施成功击败暴恐行动的净收益大于不防御时的袭击损失，即a-c1>>-b。

表1 暴恐袭击事件的策略式要素博弈模型

如表1所示，通过划线法可以得出，在该博弈中不存在纯策略纳什均衡，仅存在混合策略纳什均衡。假设政府选择采取防御行为D的概率为x，恐怖分子选择采取袭击行为A的概率为y，那么，政府g与恐怖分子t的期望收益分别为：

ug(x,y)=x[y·(a-c1)+(1-y)·(-c1)]+(1-x)y·(-b)

(1)

ut(y,x)=y[x·(-f-c2)+(1-x)(e-c2)]

(2)

求解下列最优化一阶条件，

(3)

得混合策略纳什均衡为：

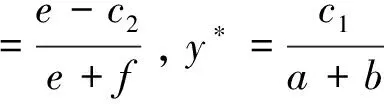
(4)

在现有的演化博弈理论中，要素博弈模型都是基于表1所示的策略式博弈，在此基础上双方群体成员进行匿名的重复博弈，获得更高收益的策略被广泛地模仿学习[17]。但是，对于暴恐袭击事件等现实管理问题，双方行动并非同时进行，而是存在着先后顺序。首先，政府反恐力量对具有较高价值的防御目标进行防御部署；其次，恐怖分子搜集获取相应的防御信息后，针对薄弱环节发动暴恐袭击。扩展式要素博弈模型如图1所示。该模型的子博弈完美纳什均衡路径为{防御，不袭击}。

图1 暴恐袭击事件的扩展式要素博弈模型

2.2 学习动态方程

在短时期的分析范围内，即一次性暴恐袭击事件中，无论政府反恐力量还是恐怖分子均很难进行适应性策略调整。但是，如果我们的分析范围扩大到较长时期，则无论政府还是恐怖分子的策略均发生了适应性学习调整。例如，911事件后随着美国加大本土反恐措施力度，恐怖分子很难再次策划劫机行动。恐怖袭击呈现出汽车炸弹、自杀式人体炸弹、独狼式袭击和针对海外人员的袭击等新特点。

一种被广泛采用的学习动态方程是复制动态方程(Replicator Dynamic)，即参与者选取某种策略s的增长率dθ(t)/dt不仅与该时期t选取该策略的人数比例θ成正比，而且与选择该策略的收益与平均收益的差值成正比[20]：

dθ(t)/dt=θ(t)·[u(s)-∑sp(s)·u(s)]

(5)

其中，θ(t)为成员选择该策略的群体比例；u(s)为选择该策略的收益；p(s)为选取该策略的概率。

正如Friedman指出的，基于扩展式要素博弈的演化分析面临着理论上的难点[17]。因为演化博弈涉及到参与者群体在不同阶段的代际模仿行为，而作为模仿基础的扩展式博弈本身即存在着后行动者对于先行动者策略选择的观察模仿行为。这大大增加了代际模仿行为的复杂性。对此，Cressman提出了而基于子博弈单调性的怀特流形分析方法[18]。在此基础上本文将心智模型的概念引入到演化博弈中，即通过考虑社会规范因素，简化了扩展式演化博弈分析过程。

3 恐怖袭击演化模型的怀特流形解

3.1 基础理论介绍

为了分析扩展式演化博弈的均衡结果，Cressman提出了基于子博弈单调理论的怀特流形求解方法。为了说明扩展式演化博弈的均衡分析过程，Cressman给出三个概念怀特流形、ω-限制点和ω-单调的如下定义[18]。

定义3(ω-单调)：假设Γ是一个具有N个参与者的完美信息博弈，en,i为第n个参与者的第i种策略，xn,i为第n个参与者选择该策略的概率，πn(en,i,x)为选择该策略的预期收益，如果Γ内部路径C满足下列条件，则称C是关于Γ的ω-单调：

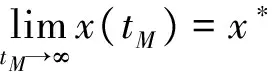
下面的定理阐述了怀特流形与子博弈ω-单调的关系，以及在子博弈ω-单调路径上ω-限制点与纳什均衡NE的关系[18]。

定理1：如果Γ是一个具有N个参与者的完美信息博弈，Γu是Γ的子博弈，那么对于N个参与者的复制动态，模型的怀特流形Wu是恒定的，并且Wu上的任何复制动态路径都是关于子博弈ω-单调的。同样地，博弈模型Γ的怀特流形W也是恒定的，且W上所有内部路径都是子博弈ω-单调的。

定理2：如果Γ是一个具有N个参与者的完美信息博弈，C是一个内部子博弈ω-单调路径，那么C所有ω-限制点都是NE，且具有相同均衡路径。

3.2 恐怖袭击事件怀特流形演化解的求解

表2 扩展式博弈中不同策略组合的收益矩阵

根据上述收益矩阵和复制动态方程(5)，可以求得扩展式博弈中恐怖分子选择策略AA和AW的群体比例增长率为：

(6)

恐怖分子选择策略AW和WW的群体比例增长率为：

(7)

政府选择不防御策略R的群体比例增长率为：

(8)

结合定义1以及上述结果可以得出，怀特流形W为：

W={(x,y)∈Δ2×Δ4|y1·y4=y2·y4

且xi≥0,yj≥0}

(9)

在怀特流形W上，恐怖分子采取策略AA和AW的群体比例增长率为：

(10)

恐怖分子采取策略AW和WW的比例增长率：

(11)

(12)

命题1:恐怖袭击事件的扩展式演化博弈模型的怀特流形演化解为(D,(0,0,1,0))，即政府始终选择防御，而恐怖分子对此只能选择不发动袭击。

4 恐怖袭击演化模型的心智模型解

由于分析扩展式演化博弈的均衡结果时，需要考虑扩展式要素博弈的策略组合，由此带来了复杂的演化结果。为了简化分析过程，本文将心智模型(Mental model)概念引入到演化博弈理论中，即考虑了社会规范后简化了参与者的可行策略空间。心智模型是一个起源于认知心理学的概念，Rouse和Morris认为心智模型是人们借以描述系统目标和形式、解释系统功能、观察系统状态以及预测系统未来状态的心理机制[21]。Akihiko的比较制度分析理论指出，心智模型又称为心智程序，指个人程序化的决策或者认知过程，它包含了一系列规则并构成了人力资产，包括两种类型的规则：认知规则和决策规则[22]。心智模型分析方法运用群体性事件等问题分析中[19]。

首先，分析政府反恐力量的认知结构。当恐怖分子选择采取袭击策略A时，政府符合常识的行为将是选择防御策略D，即xi(D|A)=1。恐怖分子采取不同策略的收益为：

u(A)=xi(D|A)·(-f-c2)+xi(R|A)·(e-c2)=-f-c2

(13)

u(W)=xi(D|W)·0+xi(R|W)·0=0

(14)

(15)

将(13-15)代入到(5)式中，可得恐怖分子的复制动态方程：

dyj/dt=yj·(1-yj)·(-f-c2)<0

(16)

由上述计算结果可知，恐怖分子选择袭击策略A的群体比例的增长率为负值，即随着时间的推移，发动袭击的恐怖分子将不断下降。而且，恐怖分析袭击策略的比例变化率dyj/dt与恐怖袭击的成本c2以及袭击失败所遭受的惩罚f成反比，与政府防御行为xi无关。

其次，分析恐怖分子的认知结构。当政府选择防御策略D时，恐怖分子符合常识的行为将是不袭击策略W，即yj(W|D)=1。对比怀特流形演化解，给定恐怖分子的上述认知结构相当于简化了表2的结构，即删除了前两列。此时，政府反恐力量采取不同策略的收益和平均收益为：

u(D)=yj(A|D)·(a-c1)+yj(W|D))·(-c1)=-c1

(17)

u(R)=yj(A|R)·(-b)+yj(W|R)·0=yj·(-b)

(18)

=xi·(-c1)+(1-xi)·yj·(-b)

(19)

将(17-19)代入到(5)式中，可得政府的复制动态方程为：

dxi/dt=xi·(1-xi)·(yj·b-c1)

(20)

由上述结果可知，政府选择防御策略D的增长率与恐怖分子选择袭击策略的比例yj、袭击成功后政府的损失b成正比，与政府防御成本c1成反比。

根据收益假设，政府遭受恐怖袭击的损失b大于防御成本b>c1。由此可以得出如下命题。

对比命题1和2，怀特流形演化解不仅计算过程比较繁琐，而且与扩展式要素博弈的均衡结果完全相同，并没有增加新的演化特征。但是，心智模型演化解不仅通过引入社会规范简化了演化分析过程，而且均衡结果展示了更为丰富的演化特征。

进一步考察恐怖分子T作为先行动者、政府反恐力量g作为后行动者的扩展式演化博弈的心智模型均衡解。由于政府和恐怖分子双方的认知结构信息均为“共同知识”，即在符合基本的有限理性假设下，对于一般的常识性结果双方均存在着理性的判断：xi(D|A)=1和yj(W|D)=1。由此导致了改变行动顺序并不影响演化博弈的均衡结果。如果双方关于认知结构的信息并不符合“共同知识”，即只有一方了解对方的认知结构，则该博弈方的分析方法应采用怀特流形演化解。

5 数值分析：以新疆6.28暴恐事件为例

5.1 事件回顾及收益值假设

本文以6.28暴恐袭击事件为案例，设定图1扩展式要素博弈的收益值。其中，由于数据难以准确获取，因此本文采用了算例分析方法，有关案例仅提供更切合实际问题的参考。

2014年6月28日中午，新疆和田地区墨玉县发生6.28暴恐袭击事件。事件发生后警方立即启动应急反应机制平息事态，并对嫌犯展开搜捕行动。墨玉县7个乡镇180个村自发参与围捕的群众达3万人以上，共同联手摧毁暴恐团伙[23]。根据新疆城镇规划网统计资料计算可得，2013年墨玉县GDP增长3.95亿元。所以，控制恐怖分子的反恐收益可视为和平发展的红利，即a=39500万元。然而，恐怖分子发动袭击成功将会导致公共安全和社会资源财富的损失，即b=39500万元。

据新华网2014年08月05日报道，新疆维吾尔自治区做出决定，拿出3亿余元重奖反恐。8月3日下午，墨玉县人民广场举行万人大会，先期对首批先进集体和个人进行表彰，奖励金额423万元。《新疆日报》2014年08月06日报道称，小时最低工资标准最高为北京和新疆，均为15.2元。由此可知，新疆最低日工资标准为121.6元，那么3万人参与围捕专项行动的成本为364.8万元。墨玉县政府的反恐投入总额包括群众的人工成本和奖励金额：c1=364.8+423=787.8万元。

2004年8月份，联合国发表一份报告，称2001年9?11恐怖袭击后，恐怖分子在制造任何一次大的恐怖袭击时，包括巴厘岛爆炸案、马德里爆炸案及伊斯坦布尔大爆炸等，成本都没有超过5万美元[24]。以此为标准，考虑汇率因素，不妨将恐怖分子发动袭击成本设为：c2=5×6.15=30.75万元。

根据2011年《刑事诉讼法修正案》，对于恐怖活动犯罪等重大犯罪案件，犯罪嫌疑人、被告人潜逃，在通缉一年后不能到案，或者犯罪嫌疑人、被告人死亡，依照刑法规定应当追缴其违法所得及其他涉案财产的，人民检察院可以向人民法院提出没收违法所得的申请[25]。根据《中国民生发展报告2014》，2012年全国家庭净财产均值为43.9万元。因此，恐怖分子发动袭击行动失败身份暴露后需要付出的涉案财产设定为：f=43.9万元。

恐怖分子发动袭击对公共安全造成的影响虽然无法准确统计，但可以通过每年各地方用于公共安全的经费支出进行估算。2013年，新疆维吾尔自治区现有88个县(市)，本级公共安全支出52.9亿元，自治区财政对各市、州、地区转移支付了45.7亿元公共安全经费，两项合计为98.6亿元，同比增长了5.6%。结合上面的数据，估算恐怖分子成功袭击的获益为：e=986000×(1+5.6%)/88=11832万元。

根据上述博弈收益值的设定，可计算出表1所示的恐怖袭击事件策略式博弈的混合策略纳什均衡为(0.9937，0.0100)。

5.2 两种均衡分析的结果对比

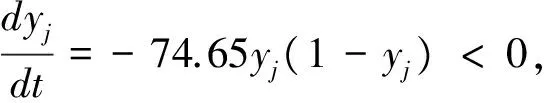
结论: 怀特流形演化解和心智模型演化解对于恐怖分析策略的收敛趋势分析一致，即恐怖分子的策略收敛到不袭击。但是对于政府策略的收敛趋势分析存在着较大差异：怀特流形演化解的结果是政府策略收敛到防御；心智模型演化解的结果是政府策略根据恐怖分子群体中选择袭击比例是否高于临界值，收敛到防御或者不防御。

6 结语

全球恐怖袭击事件频繁发生并呈现出随着反恐措施不断调整袭击方式的新特点。本文从较长时期的策略适应性调整角度，构建了恐怖袭击事件的扩展式演化博弈模型。针对扩展式演化博弈模型求解上的难点，本文将心智模型概念引入到演化博弈理论，提出心智模型演化解的求解方法，其管理含义是引入约定俗成的社会规范来简化演化分析过程。最后，结合新疆6.28暴恐事件进行了算例分析，比较怀特流形演化解与心智模型演化解的分析结果。

表3 不同演化均衡结果的对比

研究结果表明，心智模型演化解的结果中恐怖分子策略仍然收敛到不袭击，但是，对于政府反恐力量的策略收敛呈现出不同趋势：当恐怖分子采取袭击策略的比例大于临界值时，政府采取防御策略；当恐怖分子的袭击策略比例低于临界值时，政府将放弃防御行动。因此，心智模型演化解通过将普遍接受的社会规范引入到演化过程分析，不仅简化了怀特流形的分析过程，而且均衡解展示了更为丰富的、更为切合实际管理问题的演化特征。心智模型演化解具有很好的现实管理含义：在暴恐事件整体态势得到有效遏制的局面下，政府采取反恐措施应该随暴恐分子整体策略的分布变化灵活加以调整，并不存在始终如一的稳定反恐策略(或均衡解)。

在未来的研究中，可以进一步考虑具有随机特征的演化均衡解、政府与恐怖分子具有规则学习能力、考虑到双方不对称认知结构等演化问题，以及恐怖分子网络空间特征等问题。

[1] 曹颖苹, 梅建明. 对恐怖主义概念与成因的初步分析[J]. 公安大学学报, 2001, 92(4): 54-58.

[2] Sandler T, Enders W. An economic perspective on transnational terrorism[J]. European Journal of Political Economy, 2004. 302(20): 301-316.

[3] Jain S, Mukand S W. The economics of high-visibility terrorism[J]. European Journal of Political Economy, 2004, 20(2): 479-494.

[4] Ressler S. Social network analysis as an approach to combat terrorism: Past, present, and future research[J]. Homeland Security Affairs, 2006, 2(2): 1-10.

[5] Pinker E J. An analysis of short-term responses to threats of terrorism[J]. Management Science, 2007, 53(6): 865-880.

[6] Ghaffarzadegan N, Andersen D F. Modeling behavioral complexities of warning issuance for domestic security: A simulation approach to develop public management theories[J]. International Public Management Journal, 2012, 15(3): 337-363.

[7] Zhuang Jun, Bier V M. Balancing terrorism and natural disasters - defensive strategy with endogenous attack effort[J]. Operations Research, 2007, 55(5): 976-991.

[8] Wang Xiaofeng, Zhuang Jun. Balancing congestion and security in the presence of strategic applicants with private information[J]. European Journal of Operational Research, 2011, 212(1): 100-111.

[9] Zhuang Jun, Bier V M, Alagoz O. Modeling secrecy and deception in a multiple-period attacker-defender signaling game[J]. European Journal of Operational Research, 2010, 203(2): 409-418.

[10] 杨珺, 刘舒佶, 王玲. 考虑最坏中断损失下的P-中位设施选址问题的模型与算法研究[J]. 中国管理科学, 2011, 19(4): 120-129.

[11] 付举磊, 孙多勇, 肖进, 等. 基于社会网络分析理论的恐怖组织网络研究综述[J]. 系统工程理论与实践, 2013, 33(9): 2177-2186.

[12] 柴瑞瑞, 孙康, 陈静锋, 等. 连续恐怖袭击下反恐设施选址与资源调度优化模型及其应用[J]. 系统工程理论与实践, 2015, 35(1): 1-9.

[13] 刘德海, 周婷婷, 王维国. 反恐国际合作双重标准问题的序贯互惠博弈模型[J]. 中国管理科学, 2015, 23(S1): 301-309.

[14] 刘德海，周婷婷. 基于认知差异的恐怖主义袭击误对策分析[J]. 系统工程理论与实践, 2015, 35(10): 2646-2656.

[15] 郑君君, 闫龙, 张好雨, 等. 基于演化博弈和优化理论的环境污染群体性事件处置机制[J]. 中国管理科学, 2015, 23(8): 168-176.

[16] 易余胤, 盛昭瀚, 肖条军. 不同行为规则下的Cournot竞争的演化博弈分析[J]. 中国管理科学, 2004, 12(3): 126-130.

[17] Friedman D. On economic applications of evolutionary game theory[J]. Journal of Evolutionary Economics, 1998, 8(1): 15-43.

[18] Cressman R. Subgame monotonicity in extensive form evolutionary games[J]. Games and Economic Behavior, 2000, 32(2): 183-205.

[19] 刘德海. 政府不同应急管理模式下群体性突发事件的演化分析[J]. 系统工程理论与实践, 2010, 30(11): 1968-1976.

[20] Maynard Smith J. Evolution and the theory of games[M]. Cambridge, MA：Cambridge University Press, 1982.

[21] Rouse W B, Morris N M. On looking into the black box: Prospects and limits in the search for mental models[J]. Psychological Bulletin, 1986, 100(3): 349-363.

[22] Aoki M. Towards a comparative institutional analysis: motivations and some tentative theorizing[J]. Japanese Economic Review, 1996, 47(1): 1-19.

[23] 邱永峥, 王盼盼. 新疆和田发生恐怖袭击事件[N]. 环球时报, 2013-6-29,(4).

[24] 马芳. 美专家指恐怖分子7月袭击伦敦地铁仅两千美元[EB/OL]. [2006-01-04].http://sports.cctv.com/ news/world/20060104/100478.shtml.

[25] 刘晓林, 李有军. 刑事诉讼法再次“大修”[N]. 人民日报海外版, 2011-08-25,(4).