双因子非对称已实现SV模型及其实证研究

吴鑫育，李心丹，马超群

(1. 安徽财经大学金融学院，安徽 蚌埠 233030；2. 南京大学工程管理学院，江苏 南京 210093；3. 湖南大学工商管理学院，湖南 长沙 410082)

1 引言

由于波动率在金融资产组合配置、金融资产定价及金融风险管理等问题上的重要作用, 对波动率的研究一直是金融领域关注的核心问题。尤其是2007-2009年爆发的全球金融危机及至对实体经济产生的广泛影响以及我国衍生产品市场的快速发展, 进一步凸显了对金融市场波动性研究的紧迫性, 其无论是在理论上还是实践上都具有十分重要的价值。

金融市场波动率往往呈现丰富、复杂的特性。研究表明, 金融市场波动率往往表现出时变性和聚集性。两类能够成功捕获波动率的这种动态特征的模型是GARCH模型和SV模型。GARCH模型假设条件方差是历史信息集的一个确定性函数, 而SV模型假设条件方差是由一个隐含的随机过程生成。由于SV模型在条件方差过程中引入了一个新的随机过程, 其尾部拟合能力更强, 能够解释资产收益率大部分的非正态性(“尖峰厚尾”), 这使得SV模型相比GARCH模型具有更高的灵活性以及对金融时间序列更好的拟合效果[1, 2]。此外, SV模型在连续时间方面可直接与期权定价理论、利率期限结构模型等金融理论模型联系起来, 因而在实际中获得广泛的关注与应用。

基本的SV模型对于描述金融时间序列的一些经验特征事实仍过于局限。研究表明, 金融市场中利好消息(资产收益率正向冲击)和利空消息(资产收益率负向冲击)会对未来的资产价格波动产生不同程度的影响。当资产价格上涨, 未来的波动率下降, 当资产价格下跌, 未来的波动率上升, 负的资产收益率冲击对未来的波动率的影响要比相同程度的正的资产收益率冲击的影响更大, 这一现象称为波动率非对称性或杠杆效应(Leverage effects)。另外, 金融市场波动率不仅具有短期的相关性, 同时具有长期的相互影响, 即金融市场波动率具有持续性和长记忆性, 这可以通过观测资产收益率绝对值、资产收益率平方或已实现测度的自相关函数的缓慢衰减容易看到。

同时, 传统的波动率模型(例如GARCH模型和SV模型)通常采用日度收益率数据对波动率建模, 由于日度低频数据包含的信息有限, 并不能完全反映资产价格日内实际变动情况。随着电子化交易和信息存储技术的发展, 日内高频数据已经可以容易地获取得到, 基于日内高频数据构建的已实现测度在金融计量学文献中获得了越来越多的关注[3-6]。为了利用已实现测度所包含的丰富日内信息, Takahashi等[7]将已实现测度引入传统的SV模型, 构建了对日度收益率与已实现测度联合建模的已实现SV模型。基于该模型能够同时给出已实现测度的偏差与参数估计。随后, 众多学者对已实现SV模型进行了广泛的研究, 例如Koopman和Scharth[8]，Shirota等[9]、Venter和de Jongh[10]、Zheng Tingguo和Song Tao[1]。Dobrev和Szersz-en[12]、Christoffersen等[13]和Takahashi等[14]研究发现, 引入包含丰富日内高频信息的已实现测度能够显著改进SV模型参数估计与波动率估计精确性, 提高期权定价与风险度量的准确性.吴鑫育等[15]构建门限已实现SV模型对我国股市的波动性进行了考察, 发现我国股市收益率具有均值和波动率双重非对称性。基于已实现SV模型的建模思想, Hansen等[16]和Hansen和Huang Zhuo[17]对传统的(E)GARCH模型进行扩展, 构建了已实现(E)GARCH模型, 实证研究发现其比传统(E)GARCH 模型具有更好的数据拟合效果。

目前, 国内主要集中于对已实现GARCH模型的研究, 例如王天一和黄卓[18-19], 王天一等[20], 唐勇和刘微[21], 黄友珀等[22-23]。但对已实现SV模型的研究还非常少见, 且已有关于已实现波动率模型的研究较少综合考虑了金融市场波动率的非对称性与长记忆性。最近,Asai等[24]构建了同时考虑波动率非对称性与长记忆性, 对已实现波动率测度建模的波动率模型, 但该模型没有考虑到已实现测度作为真实波动率的代理存在的偏差(由非交易时间和市场微观结构噪声导致)。此外, 该模型也没有对资产收益率建模, 这给需要估计资产收益率条件预测分布来进行风险度量造成困难。

基于以上认识, 在考虑已实现测度的偏差修正的基础上, 本文构建对日度收益率和已实现测度同时建模的双因子非对称已实现SV(2FARSV)模型, 以综合捕获金融市场波动率的时变性、聚集性、非对称性与长记忆性, 并充分利用其包含的日度低频与日内高频联合信息集来提取波动率。本文构建的2FARSV模型与Koopman等学者[8-11]提出的模型存在区别, 本文构建的模型除考虑了杠杆效应外, 同时考虑了规模效应(Size effects), 可以更灵活地捕获波动率非对称性。为了估计2FARSV模型的参数, 本文给出灵活、有效且易于实现的基于连续粒子滤波(particle filters)的极大似然估计方法。最后, 给出基于上证综合指数和深证成份指数日内高频数据的实证研究, 将2FARSV模型与多种已实现波动率模型进行比较分析, 验证了本文提出模型的优越性。

2 双因子非对称已实现SV(2FARSV)模型

基本的SV模型的形式为：

rt=μ+exp(θt/2)εt,θt=c+ht,εt～i.i.d.N(0,1),t=1,…,T

(1)

(2)

(3)

其中rt是t时刻的资产收益率,ht是均值调整的对数波动率(θt是对数波动率), 服从高斯AR(1)过程,φ度量波动率的持续性, 在参数约束|φ|<1下, 波动率过程是平稳的,εt与ηt相互独立。

基本的SV模型对于描述资产收益率的波动率的一些重要特征事实仍过于局限, 例如波动率非对称性和长记忆性。此外, 基本的SV模型仅利用低频日度收益率数据对波动率建模, 没有考虑包含丰富日内信息的高频数据, 造成信息的损失和波动率估计偏差。基于此, 本文将基于高频数据构建的已实现测度引入基本的SV模型, 构建包含低频(日度收益率)与高频(已实现测度)联合信息集且能够同时捕获波动率非对称性与长记忆性的2FARSV模型对波动率建模。2FARSV模型的具体形式为:

rt=μ+exp(θt/2)εt,θt=c+h1,t+h2,t,εt～i.i.d.N(0,1),t=1,…,T

(4)

(5)

(6)

(7)

其中xt是t时刻的对数已实现测度, 已实现测度度量方程(5)的扰动项ut与εt,η1,t和η2,t均相互独立。

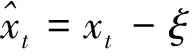
2FARSV模型通过式(6)引入了双因子(两个相互独立的AR(1)过程)来捕获波动率过程的长记忆相关性。假设-1<φ2<φ1<1, 保证波动率因子过程h1,t和h2,t是平稳的且可识别, 其中第一个因子代表波动率长期成份(持续性/长记忆波动率因子), 第二个因子代表波动率短期成份(非持续性/短记忆波动率因子)。同时, 两个波动率因子过程中均引入了非对称效应函数τi(εt),i=1,2, 捕获波动率非对称性(波动率对于资产收益率正向冲击和负向冲击的非对称反应)。本文假设τi(εt),i=1,2, 具有如下形式:

τi(εt)=τi,1εt+τi,2(|εt|-E|εt|),i=1,2

(8)

3 估计方法

本文采用基于粒子滤波的极大似然方法来估计2FARSV模型的参数。最简单和常用的粒子滤波方法是由Gordon等[26]提出的抽样重要性重抽样(Sampling/Importance resampling, SIR)滤波方法。然而, 基于标准的SIR滤波算法得到的SV模型的似然估计并非参数的连续函数, 这给采用传统的优化方法来最大化相应的似然函数造成困难。为了克服这个问题, 本文运用Malik和Pitt[27]提出的连续重抽样方法, 构建相应的连续SIR(CSIR)算法来获得连续的似然函数, 进而结合极大似然方法对2FARSV模型的参数进行估计。

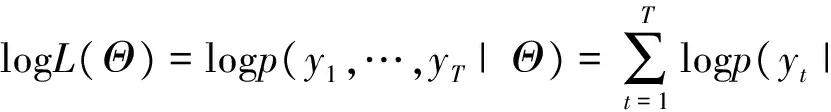
(9)

其中

(10)

它可以通过蒙特卡罗模拟近似得到, 即：

(11)

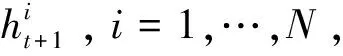
根据贝叶斯原理有：

(12)

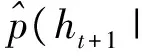
(13)

为了从式(13)中抽样, 可以利用Gordon等[26]提出的SIR滤波方法。

下面给出2FARSV模型的SIR滤波算法如下:

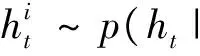
步骤2: 计算归一化权重

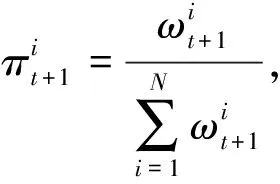
其中

基于SIR算法, 可以得到似然估计为：

(14)

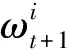
(15)

上述对数似然估计不是无偏的, 进行偏差修正得到无偏的对数似然的估计为：

(16)

其中

基于上述标准的SIR算法得到的似然估计并非参数的连续函数, 这给借助优化方法来最大化相应的模拟似然函数造成阻碍, 同时无法采用常规方法来计算参数估计的标准误差。基于此, 将SIR算法步骤3中的重抽样修正为Malik和Pitt[27]提出的连续(分层)重抽样, 由此SIR算法修正为CSIR算法。基于CSIR算法可以得到连续的似然函数估计, 进而结合极大似然方法容易得到2FARSV模型参数的估计为：

(17)

4 模拟实验

这部分构建蒙特卡罗模拟实验检验第3部分给出的基于连续粒子滤波(CSIR)的极大似然估计方法的精确性和有限样本性质。考虑2FARSV模型, 真实参数值设定为表1中给出的值。根据“真实的”2FARSV模型(4)-(8)模拟生成样本长度为T=2500的观测序列, 对该观测序列运用基于连续粒子滤波的极大似然方法进行估计, 重复模拟和估计实验100次获得参数估计的均值、标准差和均方根误差(RMSE)。基于连续粒子滤波的极大似然估计方法采用MATLAB软件编程, 在Windows 7操作系统上实现。

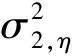
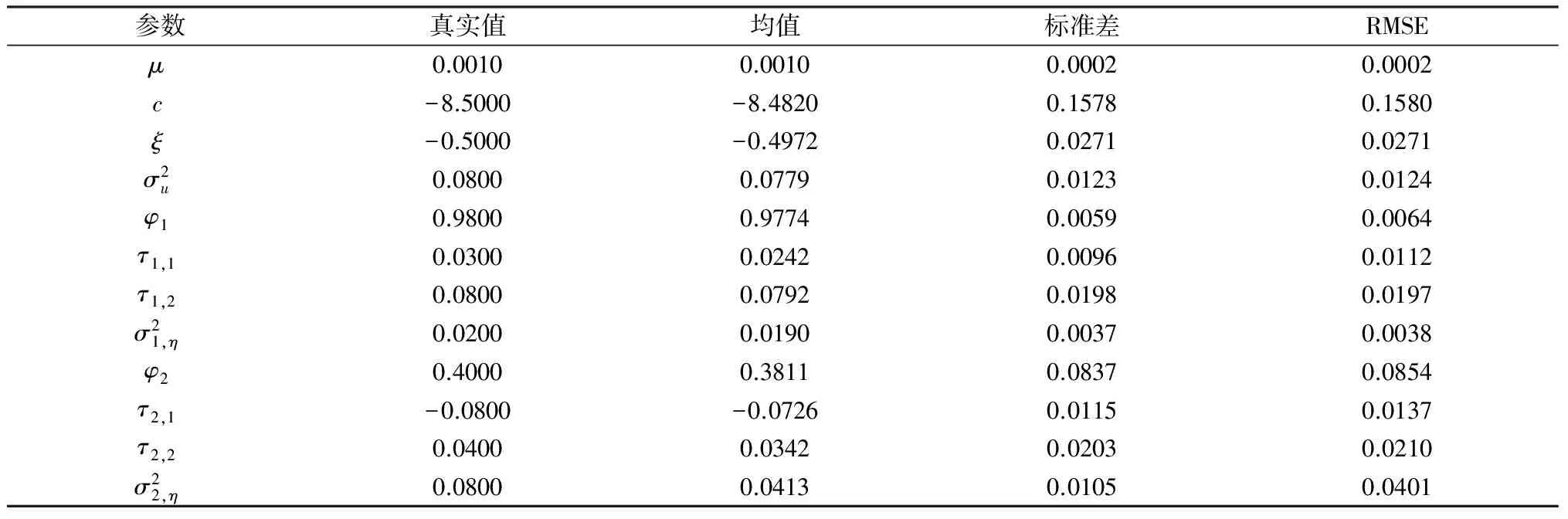
表1 数值模拟结果

注: 粒子数选取为500, 重复模拟实验100次获得参数估计的均值、标准差和均方根误差(RMSE).

5 实证研究

5.1 数据与已实现测度

本文采用上证综合指数和深证成份指数从2005年1月4日至2015年12月31日共2671个交易日的5分钟高频交易价格数据作为研究样本。所有数据均来源于天软数据库。第t交易日的指数对数收益率定义为rt=logPt-logPt-1, 其中Pt是第t交易日的指数收盘价格。资产收益率的真实日度波动率并不能直接观测到, 学者们已经提出采用日内高频交易数据构建已实现测度来给出它的估计量, 例如Barndorff-Nielsen和Shephard[4]提出已实现波动率(RV), Martens和van Dijk[28]提出已实现极差波动率(RRV)。第t交易日的RV和RRV分别定义为：

其中rt,i=logPt,i-logPt,i-1是第t交易日的第i个日内对数收益率,Pt,i是第t交易日的第i个时间间隔上的收盘价,Ht,i和Lt,i分别是第t交易日的第i个时间间隔上的最高价和最低价。RV采用单位时间间隔上的收盘价计算得到, 难以反映连续时间上的价格变化。RRV通过利用单位时间间隔上的最高价和最低价提高了日内高频信息的利用率, 研究表明RRV是比RV更有效的波动率估计量[29-30].

表2给出了上证综合指数和深证成份指数日度收益率与已实现测度(RV与RRV)的描述性统计量。从表2可以看到, 两指数日度收益率的均值都大于0, 但在统计上不显著; 偏度小于0, 峰度大于3, 表明两指数日度收益率分布呈现负偏和尖峰特征; Jarque-Bera统计量显著, 拒绝其正态性假定。两指数已实现测度(RV与RRV)的偏度、峰度和Jarque-Bera统计量都拒绝其为正态分布的假定。但比较对数已实现测度(log RV与log RRV)与已实现测度(RV与RRV)可以看到, 对数已实现测度的偏度、峰度和Jarque-Bera统计量都大大降低, 虽然并不是完全服从正态分布, 但已经较为接近于正态分布。图1和图2给出了上证综合指数和深证成份指数已实现测度时间序列图及其对数的自相关函数图。从图1和图2可以看出, 两指数在抽样阶段内均展现明显的波动率时变性和聚集性特征, 对数已实现测度的自相关函数都是缓慢衰减的, 表明其具有长记忆特征.

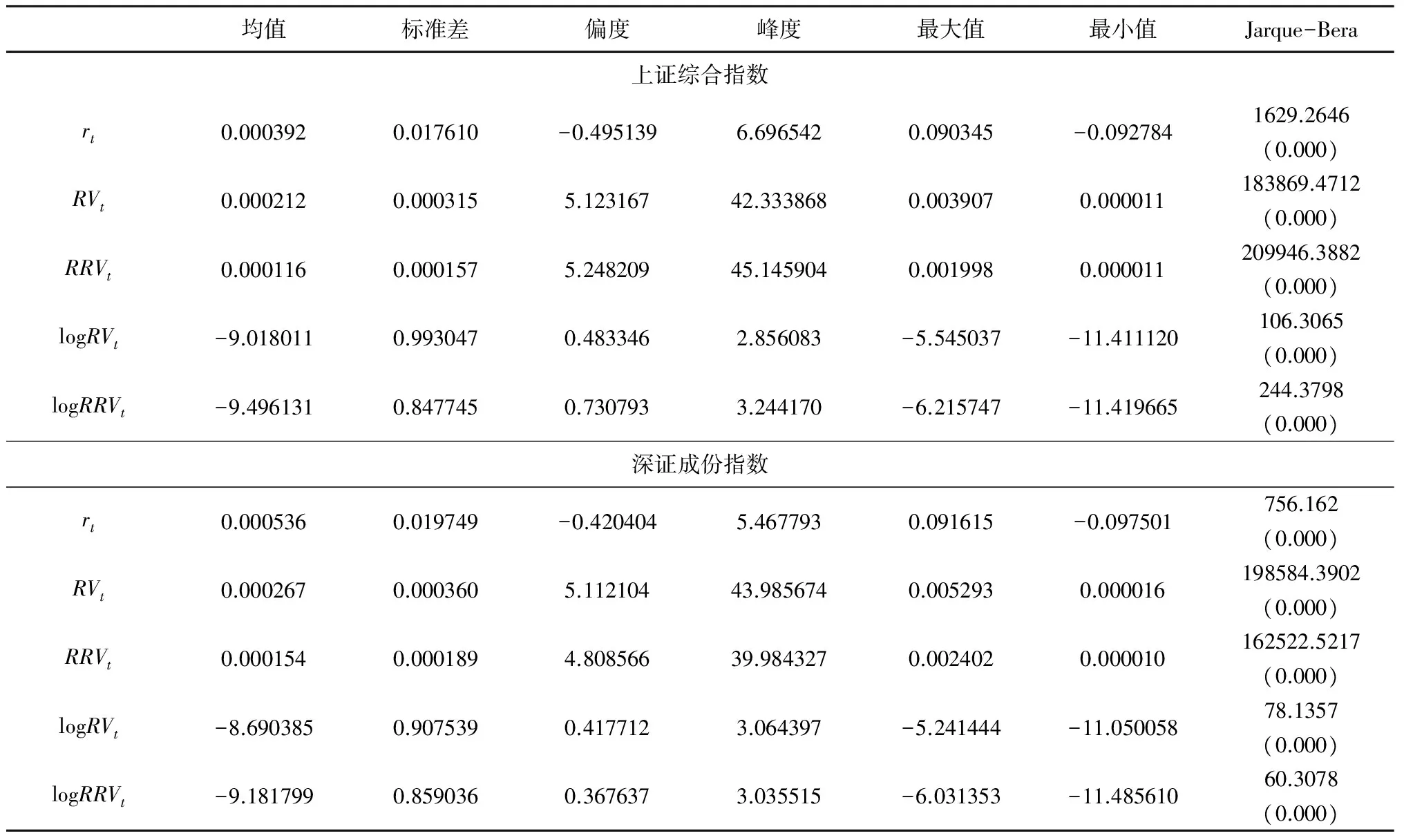
表2 指数日度收益率与已实现测度的描述性统计量

注: ()中是Jarque-Bera统计量的P-值.

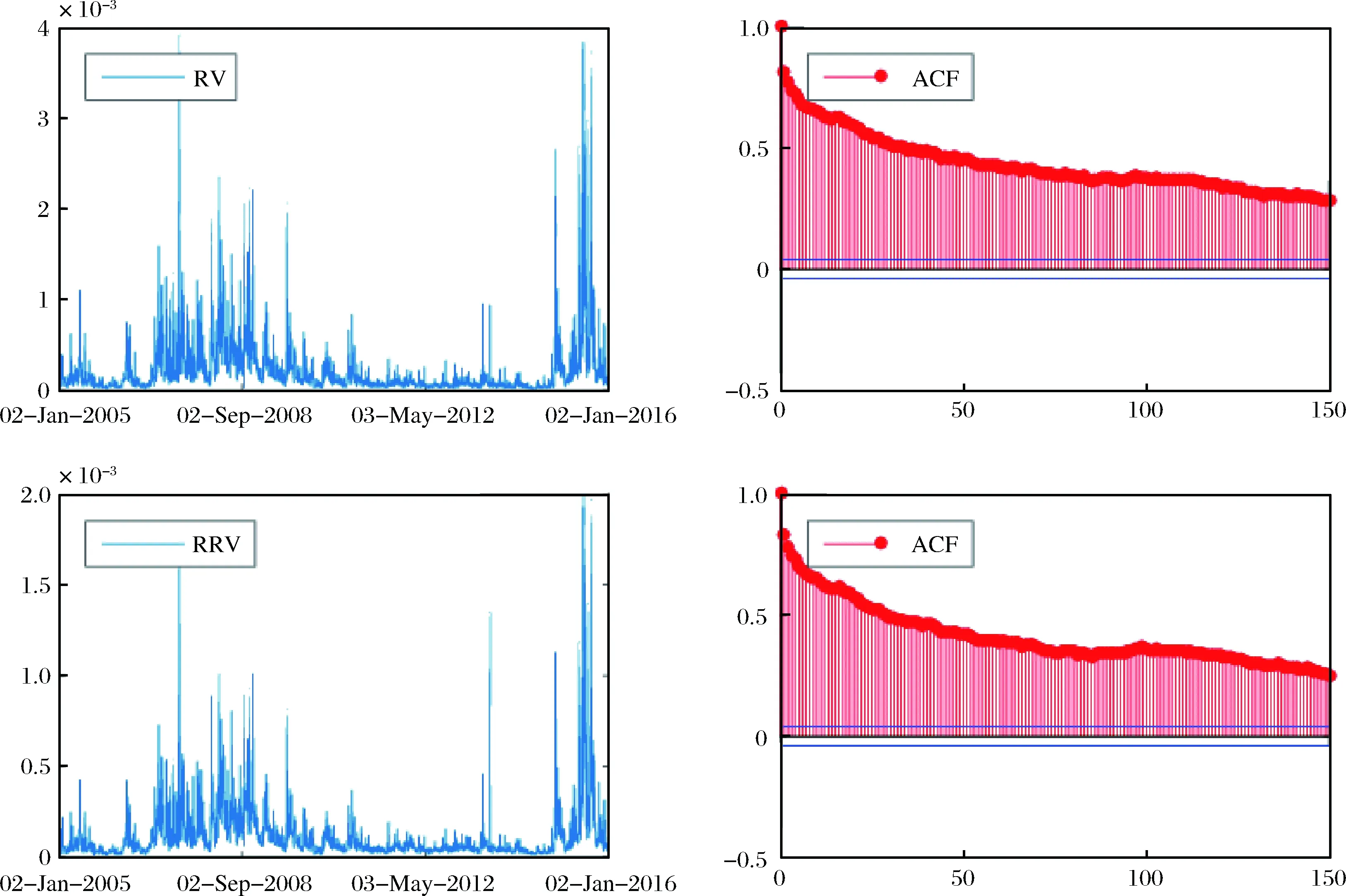
图1 上证综合指数已实现测度(RV与RRV)时间序列图及其对数的自相关函数图

图2 深证成份指数已实现测度(RV与RRV)时间序列图及其对数的自相关函数图

5.2 参数估计结果

基于5.1节给出的上证综合指数和深证成份指数数据, 运用第3部分给出的基于连续粒子滤波的极大似然估计方法, 得到2FARSV模型的参数估计及标准误差、对数似然值、赤池信息准则(AIC)和贝叶斯信息准则(BIC)如表3和表4所示。为了比较起见, 表中也给出了2FARSV模型的几种特殊形式的估计结果, 这些特殊模型包括单因子非对称已实现SV(1FARSV)模型, 双因子已实现SV(2FRSV)模型(在2FARSV模型中约束τi,1=τi,2=0,i=1,2), 以及双因子杠杆已实现SV(2FLRSV)模型(在2FARSV模型中约束τi,2=0,i=1,2)。

从表中可以看到, 上证综合指数和深证成份指数已实现测度RV和RRV的偏差修正参数ξ的估计值均明显小于0, 表明两指数已实现测度RV和RRV均存在下偏, 市场非交易时间效应强于微观结构噪声效应。RRV的偏差修正参数ξ的估计值相比RV的偏差修正参数ξ的估计值明显要更低(绝对值更大), RRV的度量标准差σu的估计值要小于RV的度量标准差σu的估计值, 表明RRV是比RV更有效的波动率估计量, 但同时RRV对于真实日度波动率的估计相比RV更倾向于下偏。所有模型中波动率持续性参数φ1的估计值均接近于1, 表明沪深股市具有强的波动率持续性特征。比较单因子模型(1FARSV模型)与双因子模型(2FRSV模型、2FLRSV模型与2FARSV模型)的估计结果可以看到, 双因子模型相比单因子模型具有更高的对数似然值和更低的AIC和BIC值, 表明能够描述波动率长记忆性的双因子模型通过引入第二个波动率因子过程显著改进了模型的拟合效果。特别地, 2FRSV模型相比1FARSV模型具有更好的数据拟合表现, 表明在波动率模型中考虑波动率长记忆性(双因子波动率)相比波动率非对称性更为重要。

在1FARSV中, 两指数τ1,1的估计值均为负值, 表明我国沪深股市存在杠杆效应。在2FLRSV模型和2FARSV模型中, 两指数τ1,1的估计值均为正值,τ2,1的估计值均为负值, 表明沪深股市杠杆效应只存在于短记忆波动率因子过程中, 长记忆波动率因子过程中存在反向杠杆效应。考虑杠杆效应的双因子模型(2FLRSV模型和2FARSV模型)相比没有考虑杠杆效应的双因子模型(2FRSV模型)具有明显的改进(获得更高的对数似然值和更低的AIC和BIC值)。在1FARSV模型和2FARSV模型中, 得到规模效应参数τ1,2与τ2,2(2FARSV模型)的估计值显著为正, 且对于2FARSV模型,τ1,2>τ2,2, 表明长记忆波动率因子过程的规模效应要强于短记忆波动率因子过程的规模效应。从各模型的对数似然值、AIC和BIC来看, 能够综合描述波动率非对称性(包括杠杆效应和规模效应)与长记忆性的2FARSV模型在沪深股市均具有比其它模型更好的数据拟合效果。

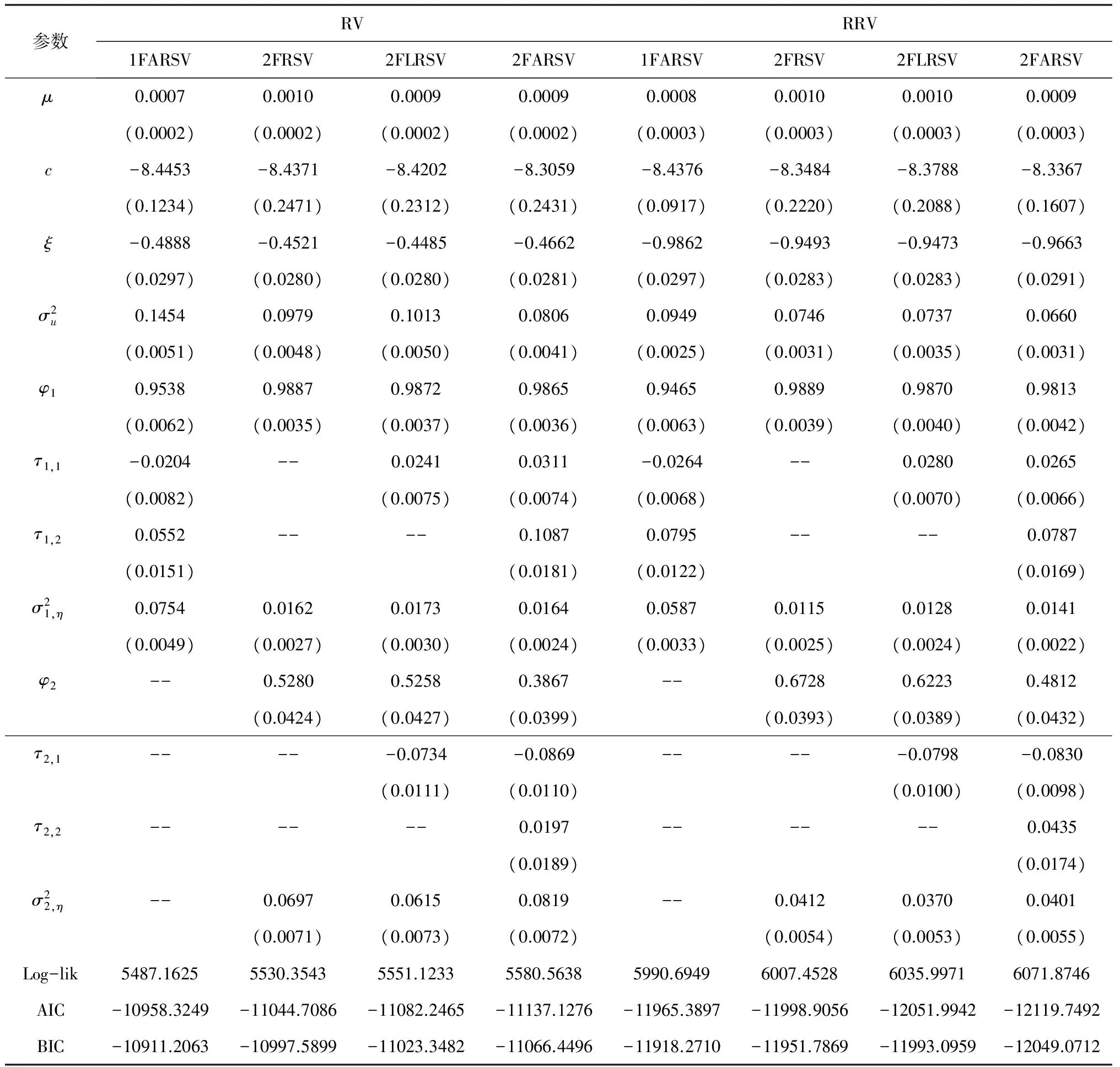
表3 参数估计结果: 上证综合指数

注: 粒子数选取为500, Log-lik是对数似然值, AIC是赤池信息准则, BIC是贝叶斯信息准则, ()中是极大似然估计的渐近标准误差.

表4 参数估计结果: 深证成份指数

注: 粒子数选取为500, Log-lik是对数似然值, AIC是赤池信息准则, BIC是贝叶斯信息准则, ()中是极大似然估计的渐近标准误差.

为了进一步凸显本文构建模型的合理性与优越性, 下面给出已实现GARCH模型[16]的估计结果作为比较。已实现GARCH模型的形式为:

rt=μ+exp(ht/2)zt,zt～i.i.d.N(0,1)

(18)

ht=ω+βht-1+γxt-1

(19)

(20)

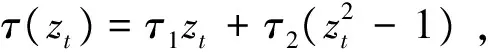
采用极大似然方法可以容易地估计已实现GARCH模型, 得到其估计结果如表5所示。从表5可以看到, 基于已实现GARCH模型获得类似于2FARSV模型的估计结果, 例如已实现测度RV和RRV均存在下偏, 沪深股市均存在杠杆效应(波动率非对称性)等。但是, 比较模型的对数似然值、AIC和BIC可以看到, 2FARSV模型相比已实现GARCH模型具有明显更为优越的数据拟合效果。

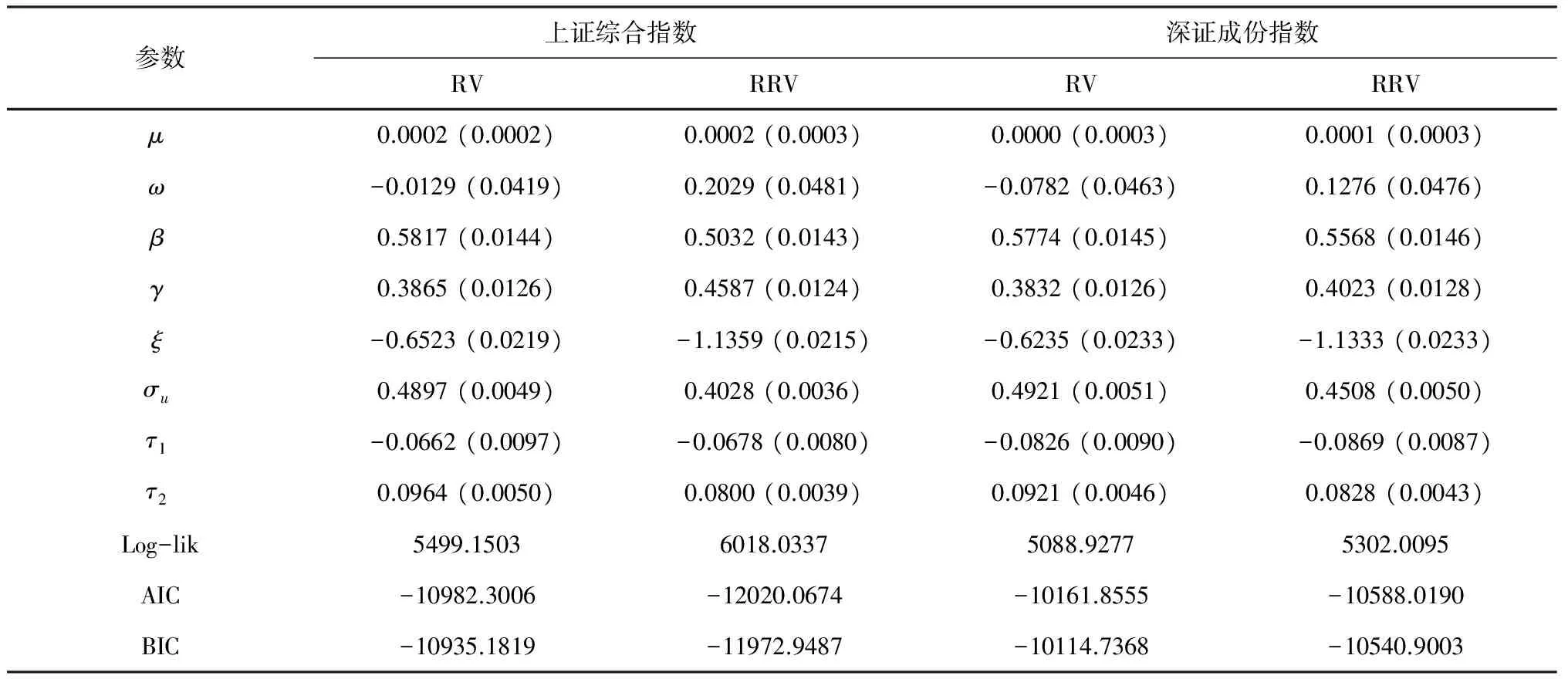
表5 已实现GARCH模型估计结果

注: Log-lik是对数似然值, AIC是赤池信息准则, BIC是贝叶斯信息准则, ()中是极大似然估计的渐近标准误差.

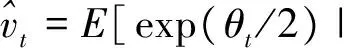
5.3 模型诊断

模型诊断通常基于标准的时间序列残差分析, 考察残差的无条件分布及动态结构。然而, 由于SV模型中隐状态变量的存在, 残差并不容易得到。但基于粒子滤波可以容易地构建“广义残差”来进行模型诊断分析。下面考虑对2FARSV模型进行诊断分析。计算分布函数

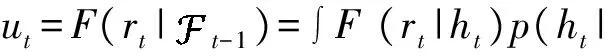
基于CSIR算法容易得到其估计为：

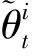
图4给出了广义残差平方的自相关函数(ACF)及广义残差的QQ图。从广义残差平方的ACF图可以看到, 广义残差平方不存在明显的序列自相关性(滞后250阶), 表明2FARSV模型成功地捕获了波动率短期和长期持续性(波动率长记忆性)。从广义残差的QQ图可以看到, 广义残差近似于正态分布, 表明2FARSV模型能够解释资产收益率大部分的非正态性, 但它对于描述资产收益率极端的左尾分布仍不充分, 说明模型存在进一步改进的可能。

图3 上证综合指数和深证成份指数波动率滤波估计

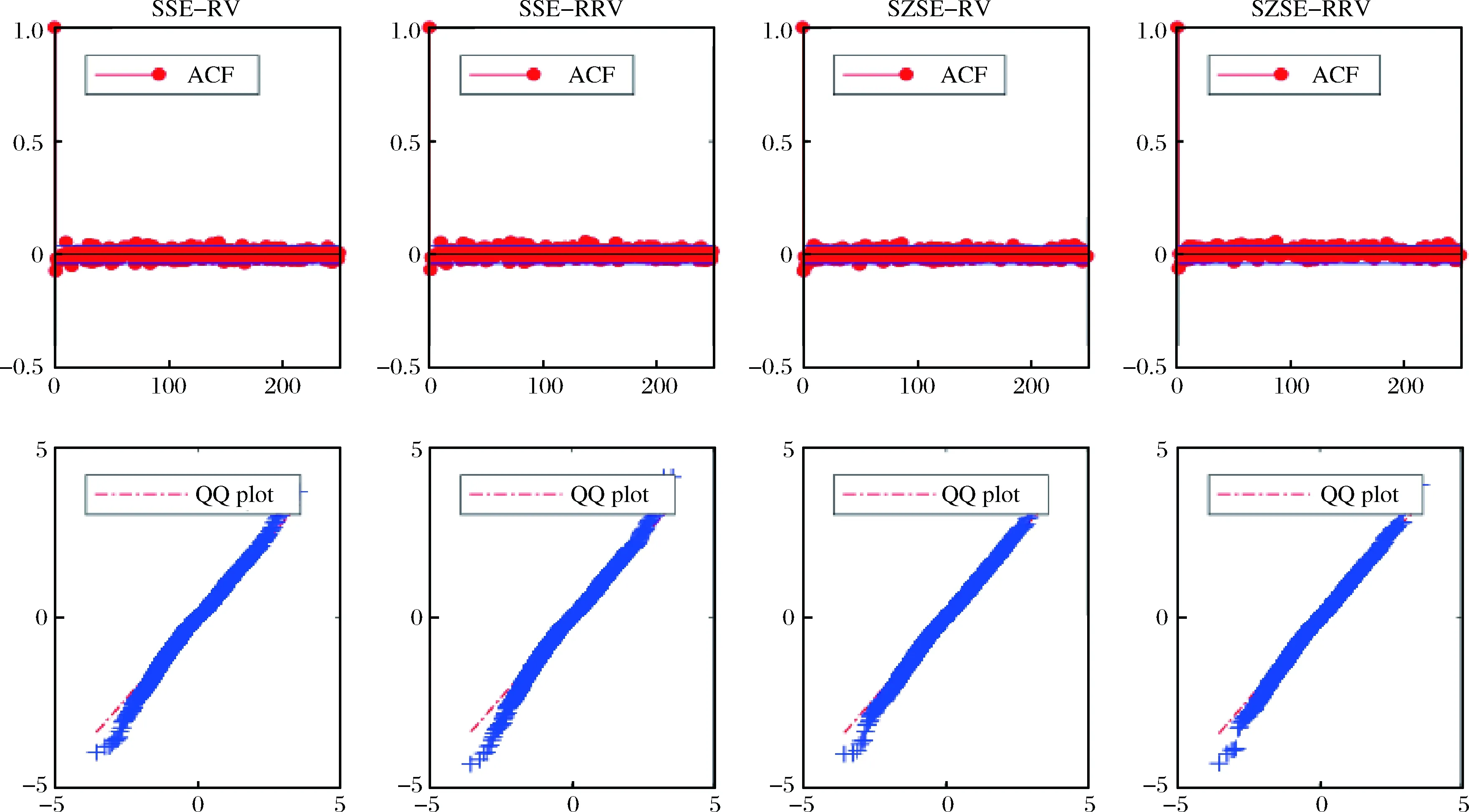
图4 广义残差平方的自相关函数(ACF)及广义残差的QQ图

6 结语

本文将包含丰富日内高频信息的已实现测度引入考虑日度低频信息的基本的SV模型中, 同时考虑已实现测度的偏差修正以及波动率非对称性(杠杆效应与规模效应)与长记忆性, 构建了包含低频与高频联合信息集的2FARSV模型。为了估计2FARSV模型的参数, 本文给出了灵活、有效且易于实现的基于连续粒子滤波的极大似然估计方法。采用上证综合指数和深证成份指数5分钟高频交易数据计算RV和RRV, 对2FARSV模型进行了实证研究。实证结果表明: RV和RRV都是真实日度波动率的有偏估计(下偏), 沪深股市非交易时间效应强于微观结构噪声效应; RRV相比RV是更有效的波动率估计量, 但同时更倾向于下偏; 沪深股市具有强的波动率持续性以及显著的波动率非对称性(杠杆效应与规模效应); 根据AIC和BIC, 2FARSV模型相比1FARSV模型、2FRSV模型以及2FLRSV模型都具有更好的数据拟合效果。模型诊断分析表明, 2FARSV模型能够充分地捕获沪深股市波动率的动态特征(时变性、聚集性、非对称性与长记忆性)。同时, 2FARSV模型能够解释资产收益率大部分的非正态性, 但对于描述资产收益率极端的左尾分布仍不充分。因此, 后续研究可以考虑对2FARSV模型进行进一步的扩展, 以改进其对于资产收益率分布形态的描述, 例如可以考虑采用学生t分布、广义误差分布或更灵活的混合正态分布等对收益率新息建模。本文的研究工作丰富了基于高频数据的波动率建模, 为市场风险管理(例如VaR的计算)、资产组合配置和期权定价提供了建模思路, 无论对于学术研究人员还是实际从业人员都具有重要的意义, 特别是对于关注全球金融风险管理的人员而言本文研究工作更具有直接的参考价值.

[1] Kim S, Shephard N, Chib S。Stochastic volatility: Likelihood inference and comparison with ARCH models[J]. Review of Economic Studies, 1998, 65(3): 361-393.

[2] Yu Jun. Forecasting volatility in the New Zealand stock market[J]. Applied Financial Economics, 2002, 12(3): 193-202.

[3] Barndorff-Nielsen O E, Shephard N. Non-Gaussian Ornstein-Ulhlenbeck-based models and some of their uses in financial economics[J]. Journal of the Royal Statistical Society: Series B, 2001, 63(2): 167-241.

[4] Barndorff-Nielsen O E, Shephard N. Econometric analysis of realized volatility and its use in estimating stochastic volatility models[J]. Journal of the Royal Statistical Society: Series B, 2002, 64(2): 253-280.

[5] 余白敏, 吴卫星. 基于“已实现”波动率ARFI模型和CAViaR模型的VaR预测比较研究[J]. 中国管理科学, 2015, 23(2): 50-58.

[6] 瞿慧, 程思逸. 考虑成分股联跳与宏观信息发布的沪深300指数已实现波动率模型研究[J]. 中国管理科学, 2016, 24(12): 10-19.

[7] Takahashi M, Omori Y, Watanabe T. Estimating stochastic volatility models using daily returns and realized volatility simultaneously[J]. Computational Statistics & Data Analysis, 2009, 53(6): 2404-2426.

[8] Koopman S J, Scharth M. The analysis of stochastic volatility in the presence of daily realised measures[J]. Journal of Financial Econometrics, 2013, 11(1): 76-115.

[9] Shirota S, Hizu T, Omori Y. Realized stochastic volatility with leverage and long memory[J]. Computational Statistics & Data Analysis, 2014, 76: 618-641.

[10] Venter J H, de Jongh P J. Extended stochastic volatility models incorporating realised measures[J]. Computational Statistics & Data Analysis, 2014, 76: 687-707.

[11] Zheng Tingguo G, Song Tao. A realized stochastic volatility model with Box-Cox transformation[J]. Journal of Business & Economic Statistics, 2014, 32(4): 593-605.

[12] Dobrev D, Szerszen P. The information content of high-frequency data for estimating equity return models and forecasting risk[R]. Finance and Economis Discussion Series，et al. Working Paper, 2010.

[13] Christoffersen P, Feunou B, Jacobs K, et al. The economic value of realized volatility: Using high-frequency returns for option valuation[J]. Journal of Financial and Quantitative Analysis, 2014, 49(3): 663-697.

[14] Takahashi M, Watanabe T, Omori Y. Volatility and quantile forecasts by realized stochastic volatility models with generalized hyperbolic distribution[J]. International Journal of Forecasting, 2016, 32(2): 437-457.

[15] 吴鑫育, 李心丹, 马超群. 门限已实现随机波动率模型及其实证研究[J]. 中国管理科学, 2017, 25(3): 10-19.

[16] Hansen P R, Huang Zhuo, Shek H H. Realized GARCH: A joint model for returns and realized measures of volatility[J]. Journal of Applied Econometrics, 2012, 27(6): 877-906.

[17] Hansen P R, Huang Zhuo. Exponential GARCH modeling with realized measures of volatility[J]. Journal of Business & Economic Statistics, 2016, 34(2): 269-287.

[18] 王天一, 黄卓. 高频数据波动率建模——基于厚尾分布的Realized-GARCH模型[J]. 数量经济技术经济研究, 2012, (5): 149-161.

[19] 王天一, 黄卓. Realized GAS-GARCH及其在VaR预测中的应用[J]. 管理科学学报, 2015, 18(5): 79-86.

[20] 王天一, 赵晓军, 黄卓. 利用高频数据预测沪深300指数波动率——基于Realized GARCH模型的实证研究[J]. 世界经济文汇, 2014, (5): 17-30.

[21] 唐勇, 刘微. 加权已实现极差四次幂变差分析及其应用[J]. 系统工程理论与实践, 2013, 33(11): 2766-2775.

[22] 黄友珀, 唐振鹏, 周熙雯. 基于偏t分布realized GARCH模型的尾部风险估计[J]. 系统工程理论与实践, 2015, 35(9): 2200-2208.

[23] 黄友珀, 唐振鹏, 唐勇. 基于藤copula-已实现GARCH的组合收益分位数预测[J]. 系统工程学报, 2016, 31(1): 45-54.

[24] Asai M, McAleer M, Medeiros M C. Asymmetry and long memory in volatility modelling[J]. Journal of Financial Econometrics, 2012, 10(3): 495-512.

[25] Asai M, McAleer M. Alternative asymmetric stochastic volatility models[J]. Econometric Reviews, 2011, 30(5): 548-564.

[26] Gordon N J, Salmond D J, Smith A F M. Novel approach to nonlinear/non-Gaussian Bayesian state estimation[J]. IEE Proceedings F-Radar and Signal Processing, 1993, 140(2): 107-113.

[27] Malik S, Pitt M K. Particle filters for continuous likelihood evaluation and maximization[J]. Journal of Econometrics, 2011, 165(2): 190-209.

[28] Martens M, van Dijk D. Measuring volatility with the realized range[J]. Journal of Econometrics, 2007, 138(1): 181-207.

[29] 文凤华, 贾俊艳, 晁攸丛, 等. 基于加权已实现极差的中国股市波动特征[J]. 系统工程, 2011, 29(9): 66-71.

[30] 郑挺国, 左浩苗. 基于极差的区制转移随机波动率模型及其应用[J]. 管理科学学报, 2013, 16(9): 82-94.