供应中断风险下OEM供应链弹性运作与提升策略

孔繁辉,李 健，2

(1.天津理工大学循环经济与企业可持续发展研究中心，天津 300384； 2. 天津大学管理与经济学部，天津 300072)

1 引言

OEM生产模式是指通过合同订购的方式，品牌企业将设计出的核心技术委托给其他企业进行生产，被委托企业只负责加工生产，品牌企业拥有自主品牌和销售渠道。OEM不断演变为一种代工生产方式，尤其在IT、家电、服装等行业，我国众多企业采用这种生产模式，从2000年到2015年，中国加工贸易出口总额从1223亿美元激增到14140亿美元，已逐渐承担全球1/3的OEM加工业务，成为真正意义上的世界工厂。

在普通的供应链网络结构中，存在多个供应商、制造商、分销商构成网络，供应链成员之间的关系是相对独立的，供应商生产的产品与多个制造商与分销商对接，而分销商上游存在多个供应商与制造商，当供应链出现中断时，供应链成员可以通过改变网络渠道避免中断风险。但是，在OEM供应链网络结构中，OEM需要承担更多网络中断的风险，这是由于，在OEM供给端，供应商数量是特定的，而且所供应的产品具有特殊性，当OEM供应商因质量、运输等生产问题不能及时交货时，分销商不能从其他途径对产品进行补给，因此要面临缺货风险[1]。例如，富士康作为苹果公司在中国的唯一OEM供应商，2013年的员工集体罢工事件，严重影响了苹果手机订单的按时交付。同理，在需求端，由于分销商销售产品的不可替代性，也将面临供应中断的风险。因此，OEM供应链网络模式与普通供应链网络结构存在差异，OEM供应链对供应链成员以及产品的特殊要求，使得OEM面临更大的中断风险。

供应链弹性问题始终是学术界关注的热点。Sheffi[2]指出弹性对于企业而言，是发生突发事件后，企业完全恢复到正常生产水平的速度，同时，指出企业通过建立冗余系统可增加弹性；Kleindorfer和Saad[3]也提出了衡量供应链弹性的标准，通过对供需端的控制使供应链恢复正常绩效水平；SerdarBakal和Katakana[4]构建了通过混合柔性实现供应链弹性；Awoken等[5-9]研究了在供应链供给和需求不确定的情况下，通过建立冗余供应链的策略可以有效预防因供应链中断所导致的系统风险。可见，供应链弹性是一个复杂的系统，分析供应链弹性运作问题，尤其是OEM供应链中弹性的运作与提升至关重要。

上述研究虽然对供应链弹性的提升有一定的作用，但是，还有以下问题需要进一步探讨：首先，供应中断会对供应链弹性的运作具有交互影响，形成多变量耦合效应，如果没有从耦合角度对供应链弹性运作进行研究，很难从根本上分析供应链弹性问题；其次，从冗余角度对供应链弹性进行提升，会增加企业的库存成本与运营负担，只有精益生产、6Sigma生产方式才能从根本上提高企业经济与社会效益。

本文主要研究OEM供应链弹性运作与提升问题。分析当面临供应中断风险时，OEM供应链中多变量交互影响机制，通过对多变量耦合效应的分析。构建一种创新机制，即深度学习，从系统量化的角度进行切入，深度学习机制能够稳定提升OEM供应链的弹性。

2 OEM供应链弹性运作

依据Sheffi等人的研究可知，弹性对于企业而言，是指当供应中断发生后的恢复生产能力的速度。因此，本文的OEM供应链弹性是指当OEM供应链出现中断时，OEM供应商自我恢复的能力，这种能力通过OEM供应链弹性运作表现出来[10-11]。

OEM供应链弹性运作是通过对OEM供应链中的企业科学管理，在面临供应中断时可以做出及时调整，从而可以最大程度较少企业损失，这种调整应具有及时性、自主恢复性、抗干扰性等[12,13]，因此，是一个多变量控制模型。OEM供应链是由多个供应商、制造商与分销商组成的供应链网络系统，分别用节点表示为：供应商Si(i=1,2,...I)，制造商Mj(j=1,2,...J)，分销商Dk(k=1,2,...K)，时间变量为t。以上节点共同构成有向图G=(V,E)，V表示OEM供应链网络{Si(i=1,2,...I),Mj(j=1,2,...J),Dk(k=1,2,...K)}，此集合是非空有限集合；E是OEM供应链网络构成的边，是一个有限集。

OEM供应链中，分销商的需求量QDk决定制造商向OEM供应商Si(i=1,2,...I)的订货数量，订货数量为QSMij(t)，提前期为LSi(t)，因此制造商生产速率表示为：

PMj(t)=f{QSMij(t),QDk(t)},i=1,2,...I;j=1,2,...J;k=1,2,...K

(1)

当分销商Dk(k=1,2,...K)需求量QDk增加时，制造商生产速率随着分销商需求量而增加，对供应商订货量也会提高，最大生产速率为PMjmax(j=1,2,...J)。

对OEM供应链网络进行分解，可得出三种OEM供应链弹性运作结构图，分别表示为图2-1

图2-1 三种OEM供应链弹性运作结构

(1)I型弹性供应链，每一个节点都是一一对应的，如果某一节点出现问题，会导致整条供应链失效，例如一些定制产品就是这种OEM供应链。供应商Si(i=1,2,...I)的供货量QSMij{t-LSi(t)}决定制造商Mj(j=1,2,...J)的产量：

PMj(t)={QSMij[t-LSi(t)]|i=1,2,...I},j=1,2,...J

(2)

(2)II型弹性供应链，存在一对多的节点，如果供应商节点出现问题，会导致下游多条供应链失效，例如IT硬件供应商问题。供应商Si(i=1,2,...I)的供货量QSMij{t-LSi(t)}和同类制造商的需求量决定制造商Mj(j=1,2,...J)的产量：

(3)

(3)III型弹性供应链，存在多对一的节点，也就是存在采购冗余，即当供应商出现问题时，制造商会出现多源订货的情况。所有供应商Si(i=1,2,...I)的供货量表示为：QSMij{t-LSi(t)}决定制造商Mj(j=1,2,...J)的产量：

(4)

I型与II型弹性供应链都会发生由于供应商的缺货问题影响制造商的生产速率问题，而III型弹性供应链制造商存在多源订货，其生产速率大于供应商的供货量。制造商的库存可以表示为：

QMj(t)=QMj(t-1)+PMj(t)-QDk(t)

(5)

依照三种弹性供应链中供应商和制造商的相互影响关系，产品输出时间Y(t)与供应链输出时间U(t)进行变换，得出Y(s)与U(s)，可将OEM弹性供应链传递函数表示为：

(6)

3 OEM供应链弹性耦合系统分析

3.1 OEM供应链弹性的多变量耦合模型

OEM供应链中的企业是依照客户需求按一定的比例进行订单的下发以及生产和销售，因此，OEM供应链弹性是多变量耦合的PID比例积分控制模型，把供应商Si(i=1,2,...I)节点与制造商Mj(j=1,2,...J)节点组成耦合系统[14]，此时，某一个输入供应商的行为会影响多个输出制造商，而某一个制造商也会影响多个供应商，如图3-1：

图3-1 OEM弹性供应链多变量耦合模型

图中存在多个输入与输出变量，是多个比例积分控制的解耦模型。其中，输入端包含OEM供应商订单ri(i=1,2,...I)，输出端包含OEM供应链绩效yi(i=1,2,...I)，当供应中断影响OEM供应链弹性时，图中的节点与边就会失效，造成整个OEM供应链网络结构发生改变，这里设定采样时间为T，因此，OEM供应链弹性解耦算法如下：

(7)

(8)

由(7)，把OEM供应链弹性分解为对三角与非对三角的闭环G(S)与G-1(S)，OEM供应链弹性耦合系统参数为矩阵gpq(p,q=1,2,...)，表示为如下：

(9)

同理，解耦控制因素C(s)可分解为对角与非对角，参数为矩阵cpq(p,q=1,2,...)，表示为如下：

(10)

令C(s)=0，求出解耦控制矩阵为如下：

(11)

同理，更高阶的高维多变量OEM供应链弹性解耦矩阵为如下所示：

(12)

上式中，cpq(p,q=1,2,...)是解耦系统参数，kpq(p,q=1,2,...)是解耦系统系数，因此：

cpq=kpq-(gpq+kpq)tpq

(13)

3.2 供应中断下的交互耦合分析

当OEM供应链供应出现中断时，会影响输入ri(i=1,2,...I)与输出yi(i=1,2,...I)，各个节点之间的关系表示为过程变量，输入与输出结果与节点之间的中断干扰有耦合效应，供应中断对OEM供应链各个节点输入ri(i=1,2,...I)、输出yi(i=1,2,...I)、过程变量ui(i=1,2,...I)的作用分别表示为Δri(i=1,2,...I)、Δyi(i=1,2,...I)、Δui(i=1,2,...I)，因此，新的耦合变量为如下：

(14)

(15)

当供应中断对OEM供应链产生耦合影响下，绩效输出函数为:

(16)

由上式可知，在供应中断交互耦合情况下，绩效输出函数有了显著的变化，如果想最大程度上消除供应中断时的耦合影响，就需要构建科学的解耦控制模型。由于OEM供应链弹性运作是一个多变量控制的复杂系统，若把一组输入与输出叫做一个控制通道，各个通道之间也会产生相互影响，故为每一个通道构建一种特殊的调节系统是非常困难的。

鉴于PID解耦控制模型，可以把多变量控制的OEM供应链弹性系统解耦变成单回路系统，将解耦变量中的影响OEM供应链绩效的耦合，分解为单个输入与输出的控制通道[15-17]，因此，只需要调节PID可以调节的kp、ki、kd变量数值，最终得到OEM供应链中最优的绩效结果。

当OEM供应链中发生不同程度的供应中断时，OEM弹性供应链多变量耦合系统中的耦合矩阵表示为如下所示：

(17)

(18)

4 基于深度学习的OEM供应链弹性提升策略

4.1 深度学习算法

提高弹性问题的最常用方法是BP神经网络，但是， BP神经网络只存在单一隐藏层，随着网络迭代次数的增加，BP神经网络准确抽象出数据的能力降低，容易导致结果出现误差，而改进的机器学习算法——深度学习算法，含有多个隐藏层，与传统的神经网络只有单一隐藏层相比，此算法克服了对数据的限制，通过逐层特征变换，将样本在原空间的特征表示变换到一个新特征空间，从而使分类更加准确。此外，BP神经网络算法对数据迭代所需时间由迭代次数的增加而增加，深度学习算法在处理复杂数据时实时更新数据的能力更强，这将提升供应链面临风险时决策的响应速度。

OEM供应链弹性系统中引入深度学习的方法，通过智能在线解耦，实现对多输入与多输出变量的协调控制[18]。深度学习算法是通过组合低层结构特征，从而形成更加抽象的高层表示，它是通过模拟人脑思维的方式分析数据，深度学习在弹性制造中的应用结构图如图4.1所示，该协调过程中变量可以是一个也可以是多个，完全取决于目标函数的复杂程度。

图4.1 深度学习在弹性制造中的应用

图4.1中，深度学习网络可分为多层，分别是输入层、多个隐藏层与输出层，把OEM供应链中弹性制造过程看成是一个完整的系统，整个训练过程也就是计算机进行深度信息测试，形成新的深度训练网络，从而能得出预测结果，其中TRAIN-Vi与TRAIN-Hi分别表示训练样本与训练结果，具体的训练过程如下：

联合组态的能量为：

(19)

某个组态的联合概率服从限制玻尔兹曼机分布：

(20)

由于节点之间不存在联结，所以隐藏节点之间条件是独立的，即：

(21)

然后容易得到隐藏层第j个节点为0-1的概率为：

(22)

同理，在给定隐藏层h的基础上，可视层第i个节点为0-1的概率为：

(23)

给定一个满足同分布的样本集为D={v1,v2,...vN}，学习参数为θ={W,a,b}，最大化以下对数似然函数(最大似然估计：对某个概率分布，需要选择一个参数，使得当前的预测样本概率最大)：

(24)

对4-6中最大似然函数求导，就得到最终求解结果：

(25)

在以上训练过程当中，可视层会产生向量v，通过v传到隐藏层。可视层会产生随机的输入向量，从而重构原始的输入信号，这些重构的输入信号被传递到隐藏层，得到新的h。在整个训练过程当中，首先可视向量映射到隐藏单元，可视单元被隐藏单元重构，新的可视单元再次映射到隐藏单元，从而得到新的隐藏单元。前进或后退过程就是我们所说的采

样，可视层和隐藏单元的相关性用权重来衡量。

在此过程中，训练时间会逐步减少，是由于只需要单个步骤就能够接近最大似然估计，每一层增加网络都会改进训练的准确概略，也就是越来越接近现实反应。

具体的深度信念网络框架图如图4.2所示，主要包括联合记忆、隐藏单元以及限制玻尔兹曼机训练过程，最终得到观察向量，也就是输出层。在隐藏节点当中，会根据样本的采样生产不同的测量权重与生成权重，进而输入到限制玻尔兹曼机当中。

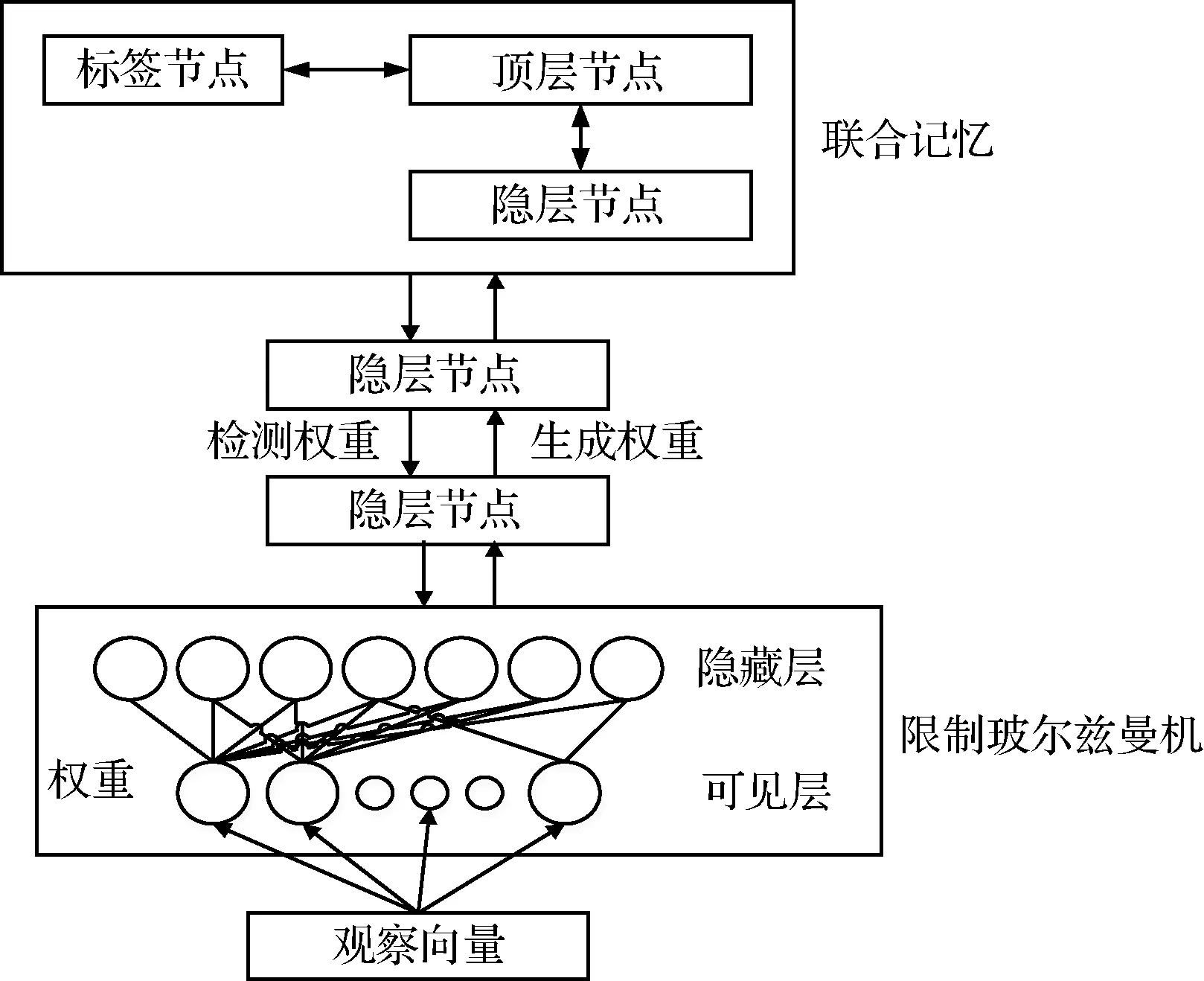
图4.2 深度信念网络框架图

4.2 案例分析与弹性提升策略

本文以某品牌空调OEM供应链为例，分别用BP神经网络与深度学习算法，对供应链绩效水平进行预测仿真，该企业作为OEM供应链，与某分销商构成OEM供应链网络，根据分析，营销供应链绩效的主要有以下4个指标，即快速反应能力、配送保障能力、运输效能、技术设备，这些指标构成BP神经网络与深度学习算法输入指标，输出指标就是期望预测的供应链绩效，该企业2013年-2015年36个月的样本数据如表4.1。表中共有36个样本数据，前24个数据作为训练样本，后12个数据作为模型预测的检验。

为使网络能加快收敛，满足适当的精度，首先对样本数据进行归一化，使得输入与输出值均在[0,1]之间。

分析分别由两个供应商、两个制造商与两个分销商组成的供应链，采样时间t=1，在约束下制造商决定系统的输入为：

P(v,h1,h2,...hl)=P(v/h1)P(h1/h2)...P(hl-2/hl-1)P(hl-1/hl)

(26)

假定，当20≤t≤25时，OEM供应链发生不可抗的供应中断，为了便于分析，分别对比弹性与非弹性制造系统，弹性制造系统具有深度学习能力，非弹性系统不具有深度学习能力，计算过程如下：

(27)

仿真月数为40个月,OEM供应链中,非弹性供应链、BP神经网络弹性供应链、深度学习弹性供应链三种系统下的供应链绩效输出如下图4.3，本训练结果的误差率是比较低的，因此，图4.3具有参考价值。

图4.3 供应链绩效训练对比图

如上图可知，当t=20时,发生供应链中断情形,弹性制造系统与非弹性制造系统都出现了供应链绩效的下滑,但非弹性制造系统的下滑深度与速率均高于弹性制造系统,到t=30左右时,中断情况终止,OEM供应链恢复到正常的供应水平,此时非弹性制造系统的绩效水平滑落到最低点0.37,而弹性系统的绩效最低点为0.42,供应链绩效明显高于非弹性系统。

除此之外，从图4.3可以明显看出，BP神经网络弹性系统比深度学习弹性系统恢复能力弱，当t=20时，二者同时降到了最低水平0.42，但是，BP神经网络需要更长的恢复时间，深度学习弹性系统在t=25时已经恢复到了正常水平，供应链绩效达到0.8左右；BP神经网络弹性系统恢复到正常水平的时间接近于第30个月，一直到40个月时，BP神经网络弹性系统的效率是递减的趋势，整体最大绩效水平只有0.6左右，远远低于深度学习弹性系统，由此可见，当OEM供应链发生中断时，深度学习弹性系统能够进行自我修复，比BP神经网络弹性系统恢复到正常绩效水平的时间更短，而且整体供应链绩效水平高于BP神经网络弹性系统。

由上述可知，当发生供应中断时，OEM供应链弹性解耦过程不仅依赖于OEM供应链中企业有形的生产运作环节宇系统，而且与业务流程、资金、信息以及企业文化有着密切的关系，应特别注意企业这些无形的因素对供应链弹性运作与解耦控制，可从以下几个方面着手：

(1)完善企业的业务流程，尤其是业务弹性，主要包括合理计算工程周期，制定弹性的作业计划，简化生产制造流程，尽量缩短生产制造周期；进行标准化生产，严格控制产品的各个生产环节，尤其是零部件的标准化生产；建立精益供应链与敏捷供应链，完善整个产品供应链的各项流程。

(2)建立科学的供应链弹性运作管理系统，利用计算机技术，发挥互联网在企业生产运作中的重要作用，利用深度学习网络进行供应链弹性运作在线智能解耦，当突发状况发生时，能够最大程度缩短应急响应时间，降低企业面临的各项风险，减轻企业各项经济损失，对整个供应链的运作发挥重要的作用。

5 结语

本文主要研究了供应中断风险下OEM供应链弹性运作与弹性提升问题。建立了多变量耦合模型以及OEM供应链弹性交互影响机制。在对解耦结果进行分析的基础上，提出了一种新的提升OEM供应链弹性的方法，即深度学习机制，此网络学习机制可以有效实现OEM供应链弹性的提升。本文研究结论如下：

(1)从OEM供应链弹性量化入手，建立了多变量耦合模型量化弹性的标准，并分析了OEM供应链中弹性交互机制，为提高OEM供应链弹性提供了可量化的参考。

(2)本文区别于以往通过增加供应链中的冗余管理的手段，而是提出了在大数据背景下的深度学习机制来提高OEM供应链弹性，从OEM供应链中企业的弹性制造与多变量耦合为切入点，建立了有效的面对供应中断时的响应机制，最后，并用实例验证了深度学习网络的科学性与可操作性，具有重要的实践价值。

由于本文的研究对象主要是OEM供应链，因此研究的是OEM供应链弹性运作与提升问题,后期可以在此研究的基础上，分析不同类型的供应链弹性问题。此外，深度学习的方法不仅可以应用到本文，而且可以适用到其他多变量解耦模型当中。

[1] Moses M, Sephardic S. Policy mechanisms for supply chain coordination[J]. IIE Transactions, 2000, 32(3):245-262.

[2] Sheffi Y. Supply chain management under the threat of international terrorism [J]. The International Journal of Logistics Management, 2001, 12(2): 1-11.

[3] Kleindorfer P R，Saad G H. Managing disruption risks in supply chains [J]. Production and Operations Management, 2005, 14(1): 53-68.

[4] Bakal I S, Katakana S. Quantity flexibility for multiple products in a decentralized supply chain[J]. Computers & Industrial Engineering, 2013, 64(2):696-707.

[5] Li Xin. A quantity-flexibility contract in two-stage decision with supply chain coordination[C]//International Conference on Computational Intelligence and Security. IEEE, 2015:109-112.

[6] Awoken S R, Singh G. Using process capability analysis to evaluate supply chain flexibility based on order lead time and order processing cost deviations[J]. European Journal of Management, 2013, 13(1):95-106.

[7] 李琳,范体军.零售商主导下生鲜农产品供应链的定价策略对比研究[J].中国管理科学,2015,23(12):113-123.

[8] Lummis R R, Delos R J V L K. Delphi study on supply chain flexibility[J]. International Journal of Production Research, 2005, 43(13):2687-2708.

[9] Seedbacher G, Winkler H. A citation analysis of the research on manufacturing and supply chain flexibility[J]. International Journal of Production Research, 2013, 51(11):3415-3427.

[10] Dietrich D M, Coney E A. Methods and considerations for the development of emerging manufacturing technologies into a global aerospace supply chain[J]. International Journal of Production Research, 2011,49(10):2819-2831.

[11] Pereira J, Hamada L, Parades F. Flexibility and amplification measures in a supply chain model[J]. IEEE, 2008:5510-5514.

[12] Stevenson M. Supply chain resilience: Definition, review and theoretical foundations for further study[J]. International Journal of Production Research, 2015, 53(18):1-32.

[13] Hinton G E, Osindero S, Teh Y W. A fast learning algorithm for deep belief nets[J]. Neural Computation, 2006, 18(7):1527-1554.

[14] Chen I J, Paulraj A. Understanding supply chain management: Critical research and a theoretical framework[J]. International Journal of Production Research, 2004, 42(1):131-163.

[15] Ho D C K, Au K F, Newton E. Empirical research on supply chain management: a critical review and recommendations[J]. International Journal of Production Research, 2002, 40(17):4415-4430.

[16] 张雨濛,王震.多级双渠道供应链的联合契约研究[J].中国管理科学,2015,23(S1):537-542.

[17] Simchi-Levi D. Review of: “Competing through supply chain management: Creating market-winning strategies through supply chain partnerships david frederick ross Chapman & Hall[J]. IIE Transactions, 2008, 30(8):762-763.

[18] Mistral D, Gunasegaram A, Papadopoulos T, et al. Big data and supply chain management: A review and biometric analysis[J]. Annals of Operations Research, 2016:1-24.