磁流变Stewart隔振平台H∞半主动控制研究

王 檑，潘忠文，廉永正，曾耀祥，陈照波

(1. 北京宇航系统工程研究所，北京 100076；2. 哈尔滨工业大学机电工程学院，哈尔滨 150001)

0 引言

在卫星的整个寿命周期内，发射过程中卫星经受的振动环境最为恶劣，这期间卫星要经受各种不同形态的准静态载荷及时变动载荷的作用。恶劣的振动环境往往是卫星发射失败的主要原因。在不改变卫星结构的前提下，在锥壳适配器与卫星之间加入Stewart六杆隔振平台，以减小卫星发射过程中所承受的振动环境和动载荷，能有效降低对卫星及其设备的动态性能的要求。

隔振平台采用磁流变阻尼器作为半主动控制器件，由于磁流变阻尼器所需能量少，具有较大的阻尼力调节范围，目前已经在航空、船舶、机械和土木工程等领域取得了一定的应用[1-4]。同时，国内外对基于磁流变阻尼器的整星隔振平台做了相关研究工作[5-7]。仿真与试验结果表明，半主动隔振平台可以取得较好的低频隔振效果。对磁流变阻尼器系统控制一般采用双层控制策略，即分为外层控制和内层控制：外层控制根据系统模型的特征得到期望阻尼力，使系统控制效果满足要求，外层控制器不需要考虑执行机构的执行能力，即按照主动控制的方式进行计算，外层控制算法主要包括天棚控制算法、最优控制、自适应控制、智能控制等[8-9]；内层控制算法的作用是使磁流变阻尼器的输出阻尼力快速跟踪期望阻尼力，但是由于磁流变阻尼器能够提供的阻尼力方向与激励性质相关，并不完全依赖输入电流，因而实际阻尼力并不能完全跟踪期望阻尼力，内层控制算法主要有开关控制、神经网络控制、模糊控制等[10-11]。针对我国运载火箭星箭界面振动环境在特定频段振动量级较大的特点，本文采用H∞控制方法[12-14]，并设计新型半主动控制策略，对特定频段振动进行重点衰减，设计控制算法，建立整星隔振平台模型，并通过仿真验证了该方法的有效性。

1 整星隔振平台动力学模型

采用Stewart平台设计整星隔振平台，如图1(a)所示，隔振平台的上、下平台分别与负载和基础相连。为了保证平台结构的对称以及便于装配时的精确调整，将上、下平台板设计为圆环形。支腿的上、下球铰通过球铰座与上下平台相连。支腿结构如图1(b)所示，支腿集成了磁流变阻尼器和弹簧，起到弹性支撑和阻尼作用。同时为满足实时控制的需要，支腿上安装了位移传感器和拉压力传感器。磁流变阻尼器置于弹簧内，与弹簧并联。弹簧选用圆截面螺旋弹簧，置于上、下挡板之间，上挡板通过轴套与上球铰相连，下挡板与螺杆相连，旋转螺杆可以调节整根支腿的长度。位移传感器通过夹具与上轴套固连。拉压力传感器与磁流变阻尼器通过轴套串接。位移传感器实测磁流变阻尼器的位移量，拉压力传感器实测磁流变阻尼器的拉压力。

(a) 平台结构

(b) 支腿结构图1 整星隔振平台Fig.1 Whole-spacecraft vibration isolation platform

磁流变阻尼器选用lord公司的rd-8040-1型阻尼器，为单出杆剪切阀式，出杆行程55mm,最大输入电流2A。阻尼器结构如图2所示，磁流变阻尼器的工作原理为：通过控制输入电流，励磁线圈产生磁场，磁流变液在不同磁场环境下具有不同的表观黏度，当活塞杆与缸体之间相对运动时，磁流变液在两个腔体间流动，产生阻碍相对运动的阻尼力。

图2 阻尼器结构Fig.2 Damper structure

对整星隔振平台建立动力学模型，如图3(a)所示，将星箭连接界面(上平台)和基础简化为刚体，即具有平动和转动共6个自由度。定义B和P分别为基础固连坐标系和上平台固连坐标系，P系原点选取为上平台质心位置xp，B系原点选取为下平台中心xB，U为惯性坐标系。为方便矢量运算转为矩阵计算，选取U、B和P3个坐标系的坐标轴方向相同,支腿两端的编号与坐标轴方向如图3(b)所示。对于位置、速度和加速度向量，其左上角的符号表示参考坐标系,对于未标明范围的物理量和坐标系下标i，其范围为1～6，对应6根支杆。

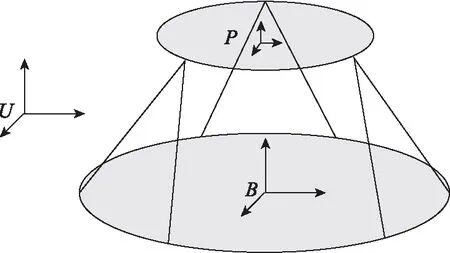
(a) 简化平台

(b)坐标系定义图3 平台空间构型Fig.3 Spatial configuration of platform

支腿两端采用球铰与上平台和基础相连，将支腿简化为上部质量和下部质量，以及连接上下部质量的弹簧和磁流变阻尼器，考虑上下两部分转动惯量，定义支杆固连坐标系Zi(i=1～6) ，原点位于qi，xi轴沿支杆方向指向pi，xi、yi、zi构成右手系，支腿各部分符号定义如图4所示。

图4 支腿动力学模型简化图Fig.4 Simplified outrigger dynamic model

刘丽坤等[15]提出了多杆被动减振平台的建模方法，在此基础上，增加磁流变阻尼力，对相关环节进行改进和修正，建立平台动力学模型。本文对相关推导进行简化和省略，详细推导过程参考文献[15]。

1.1 平台运动学方程

支杆矢量wi的角速度和角加速度为：

(UωP×Ppi)-ui×(UωB×Bqi)]/li

(1)

(2)

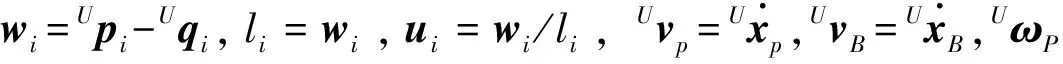
支杆上部分质量在惯性空间的加速度aui为：

ui·UvB-Bqi×ui·UωB)ui+c2

(3)

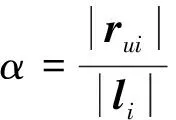
1.2 平台动力学方程

上平台的牛顿-欧拉方程为：

(4)

(5)

式中，Fsi为上平台对支杆作用力，fe、Me为卫星对上平台的力和力矩，mp、Ip为上平台的质量和转动惯量，ap、εp为上平台加速度和角加速度。

根据小幅振动分析，假定平台构型近似不变，2阶小量可以忽略不计，同时支杆长度变化量可以表示为平动和转动引起的变化量之和：

li-lri=ui·(UxP-UxP0)+Ppi×ui·θP-ui·(UxB-UxB0)-Bqi×ui·θB

(6)

式中，lri为支杆静长度，UxP0和UxB0为UxP和UxB的初始位置，θP和θB为上平台和基础绕P系和B系的卡尔丹角，在小幅振动时，有下列近似关系：

(7)

因为U、P、B和Hi坐标系三轴方向均相同，整理可以得到矩阵形式的平台线性化动力学方程为：

(8)

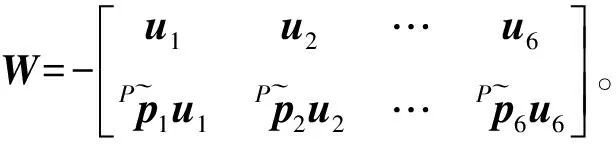
式中：

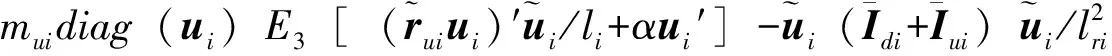
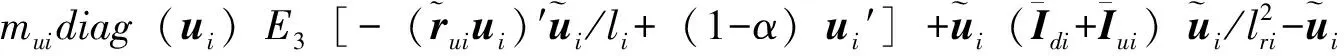
A5i=kidiag(ui)E3(ui′)

A7i=-kidiag(ui)E3[(ui)′]

2 主动控制算法

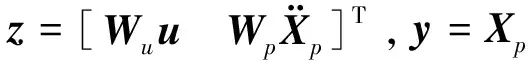
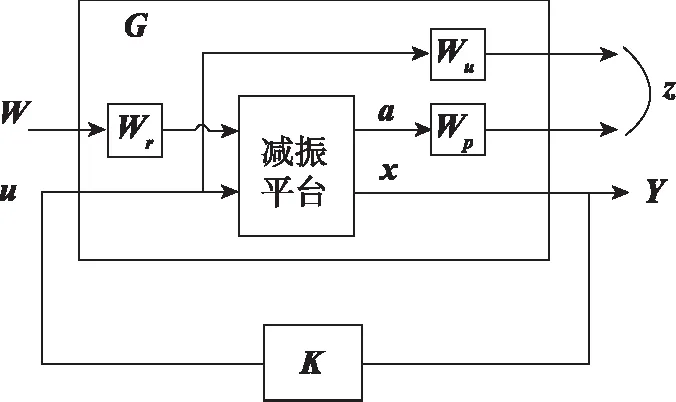
图5 H∞控制系统框图Fig.5 H∞ control system

(9)

状态空间实现为：

(10)

记为：

G=

系统传递函数与状态矩阵的关系为：

Gij=Ci(sI-A)-1Bj+Diji,j=1,2

(11)

从干扰输入w到输出z的传递函数Tzw为：

Tzw(s)=G11+G12K(I-G22K)-1G21=Fl(G,K)

(12)

通过求解两个Riccati方程可以得到控制器K(s)，使闭环控制系统稳定，并且使得：

(13)

控制器K(s)的状态空间表达为：

(14)

记为：

K=

3 半主动控制算法

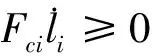
(15)

为设计半主动控制算法，需建立阻尼器力学模型，来表征阻尼器力学特性。常用数学模型有参数化模型和非参数化模型，参数化模型采用不同形式的数学函数或微分方程表征阻尼力-位移、力-速度滞回特性，非参数模型一般为神经网络模型。参数化模型中比较常用的有sigmoid模型[16]和双曲正切模型[17]，分别采用sigmoid函数和双曲正切函数进行曲线拟合。半主动控制算法中较为经典的为spencer提出的开关控制[18]，当期望阻尼力和实际阻尼力方向相同且实际阻尼力小于期望阻尼力时，输出最大电流，其他情况输出电流为0，如图6所示。由于开关控制电流在0和最大值之间切换，造成控制力跳变，会对控制对象产生一定冲击作用。为减少控制力大幅度变化，改进开关控制算法，当实际阻尼力和期望阻尼力同方向时，采用过去N个采样时刻期望阻尼力的最大值和当前时刻阻尼力的加权平均与阻尼器能提供最大阻尼力之比作为控制电流，当反向时，控制输入电流为零，如图7所示，表达式为：

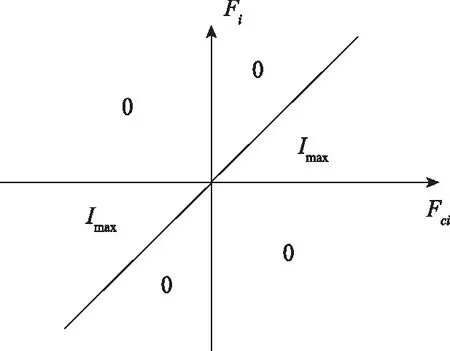
图6 开关控制算法Fig.6 On-off control algorithm

(16)

图7 改进半主动控制算法Fig.7 Improved semi-active control algorithm

4 仿真分析

合理选择平台参数，满足纵向和横向刚度要求，平台高度为0.485m，上下平台半径分别为0.432m和0.834m，支腿长度为0.7m，支腿上下两部分质量均为2kg，弹簧刚度为5×106N/m。将卫星简化为刚体，质量为1200kg，在P系中转动惯量为Ixx=Iyy=3700kg·m2，Izz=500kg·m2，Ixy=Iyz=Izx=0。由于我国CZ-2C系列、CZ-3C等型号星箭界面低频振动环境问题较为突出，如CZ-2C系列火箭40Hz振动放大现象，故以纵向振动40Hz为例，对平台上下端面传递率在特定频段进行重点衰减，选择加权函数为：

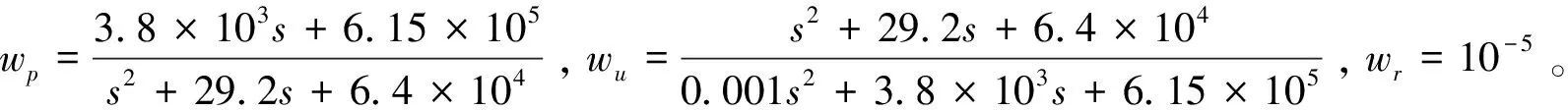
wp和wu幅频曲线如图8和图9所示。wp在40Hz处存在峰值，以增大z中40Hz频率范围内的比重；wu在40Hz处存在最小值，以较少对控制量u中40Hz分量的约束，增强控制量u在该频率段内的控制作用。

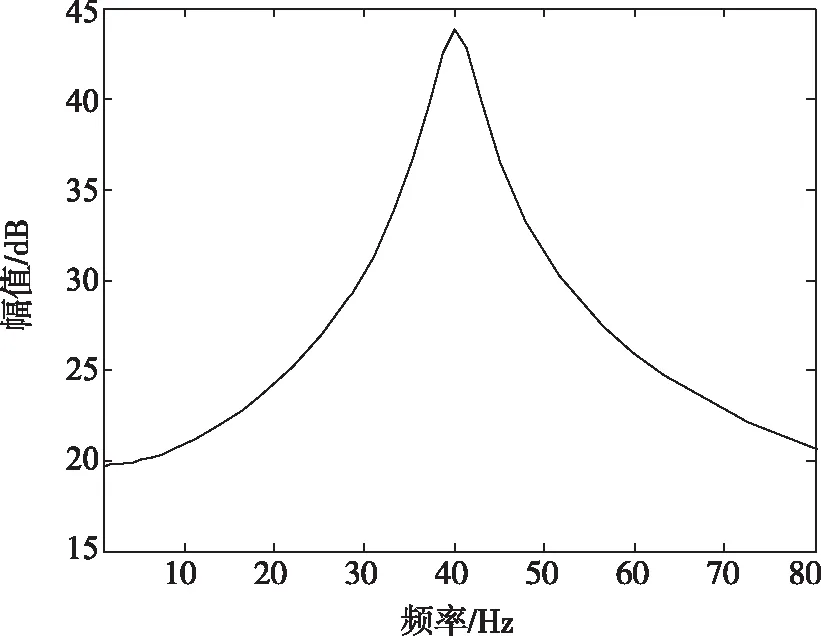
图8 wp幅频曲线Fig.8 wp amplitude frequency curve

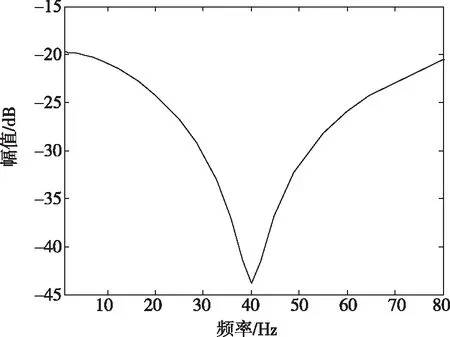
图9 wu幅频曲线Fig.9 wu amplitude frequency curve

计算得到控制器K为6自由度状态空间方程，输入为XP，输出为Fc，其纵向位移-输出力幅频与相频曲线如图10所示。

图10 控制器幅频与相频曲线Fig.10 Controller amplitude and phase frenquency curve

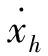
(17)

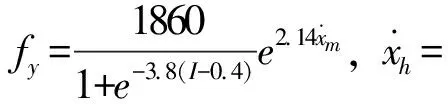
以下平台纵向振动位移xbz为输入，上平台纵向振动位移xpz为输出，考察纵向位移传递率在不同控制作用下的变化情况。纵向传递率T(s)为：

(18)

主动控制纵向振动传递率如图11所示，可以看出，采用H∞主动控制，相对被动阻尼和天棚阻尼控制算法，可以使传递率在40Hz和共振峰处均具有很大幅度的衰减，但在0～10Hz处振动有少量放大。在H∞主动控制基础上，增加理想半主动约束，纵向传递率在40Hz处的衰减作用减小，但仍然具有较好的衰减效果，同时在0～10Hz处无放大现象。

图11 主动控制与理想半主动控制纵向传递率Fig.11 Active control and ideal semi-activecontrol longitudinal transmissibility

图12 半主动控制算法纵向传递率Fig.12 Semi-active control longitudinal transmissibility

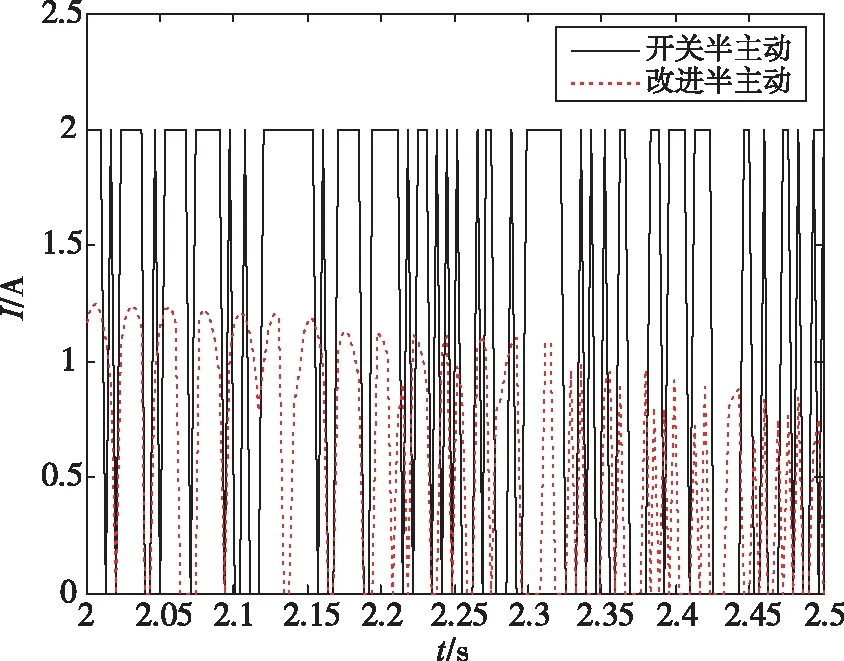
图13 半主动算法控制电流Fig.13 Semi-active control current

图14 半主动控制阻尼力Fig.14 Semi-active control force

分别采用开关控制和改进半主动控制算法，对期望阻尼力进行跟踪，纵向传递率如图12所示，可以看出，与理想半主动约束相比，采用半主动控制算法后，低频(0～55Hz)控制效果变差，共振峰与40Hz处传递率均增大，相对天棚控制在40Hz处依然具有较小的传递率；但在较高频段(55Hz～80Hz)，传递率小幅降低，与天棚控制相当。改进半主动控制与开关控制输出电流和阻尼力如图13和图14所示，采用改进半主动控制后，电流变化范围减小同时不会出现电流突变的情况，因而阻尼力没有大幅度跳变。同时从纵向传递率可以看出，改进半主动控减小了在0～5Hz传递率的波动，同时共振峰和40Hz处减振效果均有明显改善。

5 结论

采用牛顿-欧拉法建立磁流变整星减振平台动力学模型，并设计H∞主动控制算法，通过选择合适的加权函数，降低星箭界面特定频段振动，能够获得较好的控制效果。改进开关半主动控制算法，提出的改进半主动控制算法可以减小阻尼力大幅度跳变，改善阻尼力跟踪效果。上述方法可以有效改善星箭界面力学环境，具有重要的理论与工程意义。

[1] 王唯，夏品奇.采用磁流变阻尼器的直升机“地面共振”分析[J]. 南京航空航天大学学报，2003，35(3):264-267.

[2] 周云，吴志远，梁兴文. 磁流变阻尼器对高层建筑风振的半主动控制[J]. 地震工程与工程振动，2001，21(4):159-162.

[3] 王锎，何立东， 邢健，等. 磁流变阻尼器控制双跨转子轴系振动研究[J]. 振动与冲击, 2015，34(2):150-153.

[4] 夏兆旺，袁秋玲，茅凯杰，等. 船舶辅机单层半主动非线性隔振系统振动特性分析[J]. 船舶力学, 2017, 21(1):69-75.

[5] 涂奉臣. 基于磁流变阻尼器的整星半主动隔振技术研究[D]. 哈尔滨: 哈尔滨工业大学，2010.

[6] Jean P, Ohayon R, Bihan D L. Semi-active control using magneto-rheological dampers for payload launch vibration isolation[C].SPIE Symposium on Smart Structures and Materials. 2006, 6169: 61690H.

[7] 程明, 陈照波, 杨树涛, 等. 应用磁流变技术的星箭界面半主动隔振研究[J]. 振动工程学报, 2017, 30(1): 86-92.

[8] 李忠献，徐龙河. 新型磁流变阻尼器及半主动控制理论设计[M].北京：科学出版社，2012: 134-203.

[9] 吴忠强，邝钰. 汽车磁流变半主动悬架反步自适应控制研究[J]. 机械设计, 2010, 27(4): 25-28.

[10] Spencer Jr B F, Dyke S J, Sain M K, et al. Phenomenological model for magnetorheological dampers[J].Journal of Engineering Mechanics, 1997, 123(3): 230-238.

[11] 廖英英，刘永强 ， 刘金喜. 磁流变阻尼器的神经网络建模及在半主动控制中的应用[J]. 北京交通大学学报，2011，35(6): 67-71.

[12] 张志勇，刘鑫，黄彩霞，等.具有参数不确定性的车辆座椅悬架H∞输出反馈半主动控制[J]. 振动与冲击， 2013, 32(14):93-97

[13] 吴敏， 何勇， 佘锦华.鲁棒控制理论[M]. 北京:高等教育出版社， 2010.

[14] Chida Y, Ishihara Y, Okina T, et al. Identification and frequency shaping control of a vibration isolation system[J]. Control Engineering Practice, 2008, 16(6): 711-723.

[15] 刘丽坤,郑钢铁,黄文虎. 整星被动多杆隔振平台研究[J]. 应用力学学报, 2005, 22(3): 329-334.

[16] 李秀领，李宏男. 磁流变阻尼器的双sigmoid模型及试验验证[J]. 振动工程学报,2006, 19(2):168-172.

[17] Kwok N M, Ha Q P, Nguyen T H, et al. A novel hysteretic model for magnetorheological fluid dampers and parameter identification using particle swarm optimization[J]. Sensors and Actuators A: Physical, 2006, 132(2): 441-451.

[18] Spencer Jr B F, Dyke S J, Sain M K, et al. Phenomenological model for magnetorheological dampers[J]. Journal of Engineering Mechanics, 1997, 123(3): 230-238.