齿轮齿条式电涡流阻尼墙有限元数值研究
2022-10-09李寿英霍朝煜毛伟阳李亚峰陈政清
李寿英,霍朝煜,毛伟阳,李亚峰,陈政清
(风工程与桥梁工程湖南省重点实验室(湖南大学),湖南长沙 410082)
电涡流阻尼依据电磁感应原理产生阻尼,相较于传统黏滞阻尼器,电涡流阻尼具有结构简单、无机械磨损、内无流体、刚度与阻尼参数分离、阻尼系数易于调节等显著优点[1-3].湖南大学陈政清院士课题组对电涡流阻尼技术的结构减振应用进行了大量研究,开发出了多种电涡流TMD[4-6]及电涡流阻尼器[7-9],已经广泛应用在大跨度人行桥[10]、大跨度钢拱桥吊杆[11]、超高层建筑[12]、斜拉索[13]等工程中.目前,建筑结构中的电涡流阻尼技术应用主要以电涡流TMD 减小风致振动为主,但TMD 控制频率单一,结构在地震作用下没有固有的振动频率,很难实现调频[14].
黏滞阻尼墙(Viscous Damping Wall,VDW)是一种由学者Miyazaki 等[15-17]提出的墙型阻尼器,并于1992 年首次安装于高层建筑[18]中,并使结构阻尼比达到27%左右.1998 年,Yeung 等[19]验验证了VDW能有效减少结构风振响应.2005年,闫锋等[20]通过振动台试验发现VDW 能耗散60%~70% 的地震能量.2010 年,VDW 首次在国内实现应用[21].VDW 阻尼性能易受温度的影响,且国内的高性能黏滞阻尼材料研发较为滞后[22],电涡流阻尼技术的逐渐成熟使得替代黏滞阻尼成为可能,但在墙型阻尼器中的可行性需深入研究.
颜学渊等[23]提出一种具有位移放大作用的扭转阻尼器,在阻尼器中增加响应放大机构可有效提高耗能效率.利用齿轮齿条可方便地实现速度放大效应,同时可实现惯质(或称为表观质量)作用,是一种新型的减振方式[24-27].为探究电涡流阻尼在墙式阻尼器中应用的可行性,提出一种新型的齿轮齿条式电涡流阻尼墙(Eddy Current Damping-Rack and Gear Wall,ECD-RGW),介绍了ECD-RGW 的构造及工作原理,并推导了其力学性能表达式.通过电磁有限元对ECD-RGW 主要设计参数进行了分析,研究了各类参数对ECD-RGW 的阻尼性能的影响.
1 ECD-RGW 的构造及力学性能
ECD-RGW 的构造如图1 所示,可分为两个部分:第一部分是由齿条、齿轮、传动轴、轴承和钢箱组成的速度放大装置;第二部分是由永磁体、导体板和背铁组成的电涡流阻尼单元.

图1 ECD-RGW 的构造示意图Fig.1 Schematic of ECD-RGW
实际工程应用时,将ECD-RGW 的钢箱固定在下层楼面,将齿条或与齿条刚性连接的连接件固定在上层楼面,当结构受到风荷载或地震作用时,上下层楼面之间的相对运动使齿条与钢箱之间产生相对速度,进而产生阻尼力.其中,齿条与齿轮1 啮合,齿轮1 与齿轮2 同轴,齿轮2 与齿轮3 啮合,齿轮3 与导体板同轴,经过齿轮多级传动,将齿条的直线运动转化为导体板的旋转运动,并最终以热能的形式耗散.设结构上下楼层的相对运动速度为,即齿条轴向速度为当齿轮设置为两级传动时,导体板角速度为:

式中:r1、r2和r3分别为齿轮1、齿轮2和齿轮3的半径.
设导体板上产生的电涡流阻尼力矩为Te,传动到齿条上的阻尼力为Fd,不考虑能量损耗,即传动机构的输入功率等于输出功率,可得:

将式(1)代入式(2)中,可得电涡流阻尼力Fd为:

设ECD-RGW 的等效阻尼系数为ce,则有:

将式(3)代入式(4)中,并结合式(2)得:

2 ECD-RGW 的电磁有限元模拟
2.1 电磁有限元模型
采用多物理场电磁有限元软件COMSOL Multiphysics建立了ECD-RGW 的三维有限元模型,如图2所示.由于齿轮齿条速度放大装置仅对导体板的速度产生影响,因此可简化模型而仅对电涡流阻尼单元进行建模.该电磁有限元模型由阻尼单元及外部的球形空气域组成,阻尼单元主要包括永磁体、永磁体背铁、气隙、导体板、导体板背铁.计算模型单元数视工况而定,在20 万~30 万个之间,其中永磁体、导体板及其邻近空气域的网格划分最细,对背铁单元的网格划分次之,由于外部空气单元等其他区域单元网格对结果影响极小,可以忽略,因此网格划分较粗.通过有限元模拟可以得到电涡流阻尼力矩Te与导体板转速的关系,然后根据ECD-RGW 的力学性能得到电涡流阻尼力Fd与速度的关系.

图2 ECD-RGW 的有限元模型Fig.2 Finite element model of ECD-RGW
ECD-RGW 中电涡流阻尼耗能装置的横截面与几何参数如图3 所示,选取标准工况的模型参数如表1 所示,在速度放大装置中,速度放大倍率为14.50.永磁体背铁厚度为16 mm,永磁体采用N52 型铷铁硼(NdFeB)材料,长度为40 mm,径向厚度为20 mm,剩余磁感应强度Br为1.43 T;导体板采用铜板,厚度为2 mm,导电率为σ=58 MS/m,导体板与永磁体间的气隙长度为1 mm.

表1 标准工况的模型参数Tab.1 Parameters of the standard working condition

图3 ECD-RGW 的几何参数Fig.3 Geometric parameters of ECD-RGW
2.2 数值结果
图4 给出了标准工况下,电涡流阻尼力与等效阻尼系数随速度的变化曲线.从图4 中可看出:电涡流阻尼力-速度曲线先近似线性增长,后呈凸曲线非线性增长,阻尼力在临界速度=0.652 m/s时达到峰值240.49 kN,随后电涡流阻尼力随速度增加而降低.等效阻尼系数随着速度的增大不断减小.产生这种规律的原因是当速度较小时,电涡流产生的反抗磁场对原生磁场的影响也就较小,所以电涡流阻尼力先随速度增加而呈近似线性增长.速度不断增加时,反抗磁场对原生磁场的削弱影响更强,阻尼力的非线性性质也更明显.

图4 标准工况下的有限元仿真结果Fig.4 The results of FEM under standard condition
3 电涡流阻尼力参数分析
由于影响电涡流阻尼墙性能的参数较多,在上述标准工况的基础上,研究了主要设计参数对电涡流阻尼力的影响,包括导体板厚度、气隙长度、导体板材料、导体板背铁厚度和永磁体数量.
3.1 永磁体数量的影响
图5 给出了永磁体数量n=4、6、8、10 对时,电涡流阻尼力与等效阻尼系数随速度的变化曲线,表2则给出了不同数量永磁体工况的相关参数.从图5中可看出:电涡流阻尼力与初始等效阻尼系数都随着永磁体数量的增加而增大.从表2中可看到:Fd,max/n与c0/n也都随着n的增大而小幅增大,即永磁体的数量对最大阻尼力、初始阻尼系数的影响呈现出一定的非线性.这是由于永磁体数量的增多缩短了磁感应线及电涡流的流动路径,也减少了漏磁,提高了电涡流密度.但永磁体的最优数量还会受到永磁体尺寸、气隙长度等因素的影响[26],对于不同的构造需要更为详细的研究.

图5 永磁体数量的影响Fig.5 The effect of the number of permanent magnets

表2 各工况的最大阻尼力与初始等效阻尼系数Tab.2 Maximum damping force and initial equivalent damping coefficient under various conditions
3.2 气隙长度的影响
图6 给出了气隙长度Td=1 mm、2 mm、4 mm、6 mm、8 mm 时,电涡流阻尼力与等效阻尼系数随速度的变化曲线.从图6 中可看出:电涡流阻尼力与等效阻尼系数均随气隙长度的增大而减小.这是因为当气隙长度增大时,导体板上的磁感强度变小,产生的电涡流强度不断减小,从而导致电涡流阻尼力与等效阻尼系数均不断减小.在不同气隙长度下,最大电涡流阻尼力对应的临界速度几乎保持不变.这是由于导体板厚度相同,导体板上的原磁场强度、电涡流密度、反抗磁场都同步变化,因此可以对临界速度产生影响.

图6 气隙长度的影响Fig.6 The effect of length of air gap
3.3 导体板背铁厚度的影响
图7 给出了导体板背铁厚度Tb=0 mm、1 mm、4 mm、8 mm、16 mm、165 mm 与无背铁时,电涡流阻尼力与等效阻尼系数随速度的变化曲线.

图7 导体板背铁厚度的影响Fig.7 The effect of thickness of back iron plate of conductive plate
从图7 中可看出:背铁对电涡流阻尼力及等效阻尼系数具有非常重要的影响.相较于无背铁工况,背铁的存在显著提高了电涡流阻尼力,降低临界速度到一半以下.例如,速度=0.072 m/s 时的初始等效阻尼系数c0可提高到4倍以上.这是因为背铁有利于形成闭合磁路、减少系统漏磁,因此增加了导体板板内的磁通量,从而提高电涡流阻尼的耗能效率,同时也可以减小磁场对建筑使用造成的影响.背铁厚度的增加对耗能效率的提升效果并不明显,对比16 mm背铁工况,即使背铁厚度达到165 mm,阻尼力也只能提高1%~2%.对于本例,背铁厚度为1 mm时,已达到非磁饱和状态,继续增加其厚度对阻尼效应几乎无明显提升.在电涡流阻尼墙的设计中,转盘可以充当导体板背铁,且不同厚度的背铁可以产生不同大小的表观质量,ECD-RGW 可以分别控制电涡流阻尼力和表观质量惯性力的输出.
3.4 导体板材料的影响
图8 给出了导体板材料为铜、铝和锌时,电涡流阻尼力与等效阻尼系数随速度的变化曲线.其中,铜的导电率σ=58.0 MS/m 最大,铝的导电率σ=37.0 MS/m次之,锌的导电率σ=16.0 MS/m最小.

图8 导体板材料的影响Fig.8 The effect of material of conductive plate
从图8 中可看出:不同材料导体板会显著影响电涡流阻尼力的临界速度,锌材料对应的临界速度以及峰值电涡流阻尼力最大(=2.391 m/s,Fd,max=277.53 kN),铝材料次之(=1.087 m/s,Fd,max=251.88 kN),铜材料对应的临界速度以及电涡流阻尼力峰值最小(=0.652 m/s,Fd,max=240.50 kN).当电导率在较小范围变化时,峰值阻尼力变化较小;电导率改变范围较大时,峰值阻尼力变化也更明显.当临界速度≤0.724 m/s 时,导体板材料为锌时的等效阻尼系数最小,铝次之,铜最大.原因是导体板的导电性能越强,导体板上产生的电涡流的强度越大,在较低速度下就能产生较大的阻尼力,故等效阻尼系数越大.而当铜和铝材料对应的阻尼力随着速度不断下降时,锌导体板中电涡流产生的反抗磁场较小,反抗磁场对阻尼力的削弱还不足以抵消速度增大引起的阻尼力的增大,所以锌导体板的阻尼力仍随速度增大而增大.
3.5 导体板厚度的影响
图9 给出了导体板厚度Tc=1 mm、2 mm、4 mm、6 mm、8 mm 时,电涡流阻尼力与等效阻尼系数随速度的变化曲线.从图9中可看出:低速状态下(<0.145 m/s),电涡流阻尼力随着铜质导体板厚度增大而增大,等效阻尼系数也随导体板厚度增大而增大(Tc=8 mm例外).同时,电涡流阻尼力峰值Fd,max与临界速度随导体板厚度增大而减小.这因为低速状态下,导体板越厚,电涡流的分布区域就越广,阻尼力与阻尼系数也就越大,同时会相应降低临界速度与峰值阻尼力的大小.因此,在ECD-RGW 的设计中,应根据其目标工作速度区间来选取导体板的厚度.

图9 导体板厚度的影响Fig.9 The effect of thickness of conductive plate
4 ECD-RGW 的减震效果分析
通过数值模拟进行时程分析,研究了附加ECDRGW 单自由度系统的减震性能,并与土木工程结构中广泛使用的黏滞阻尼器(FVD)作比较.在地面作用下的单自由度系统的运动微分方程为:
式中:u是结构相对于地面的位移;Fd是阻尼器产生的阻尼力;üg是地面运动加速度.选用的地震波为El-Centro.单自由度简化模型如图10 所示,参数为:质量m=2.07×108kg,第一阶固有频率f=0.221 9 Hz,结构阻尼比ξ=0.02[9].
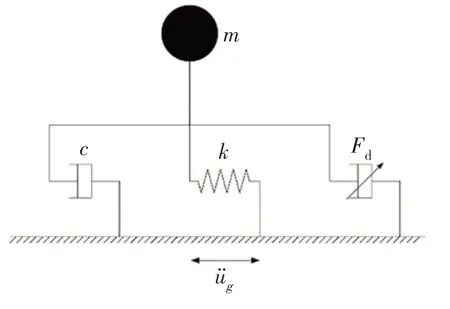
图10 附加阻尼器的单自由度结构模型简图Fig.10 The schematic model of the SDOF system with a supplemental damper
电涡流阻尼力采用Wouterse 提出的非线性数学模型[28]:

FVD的阻尼力采用忽略刚度的Maxwell模型[29]:

式中:α为阻尼指数.
采用标准工况条件下电涡流阻尼墙的阻尼力,设置FVD 在ECD-RGW 的临界速度下的阻尼力Fd与ECD-RGW 的Fd,max相等.ECD-RGW 与FVD 的阻尼力-速度曲线对比如图11 所示,可以看出FVD的阻尼力会随着速度的增加不断变大,ECD-RGW的有限元仿真结果与Wouterse 的数学模型吻合.速度在0.435~1.014 m/s 范围内,ECD-RGW 的阻尼力在Fd,max范围内变化不大,即在较宽速度范围内均能较好地发挥耗能作用.

图11 不同阻尼器的阻尼力-速度曲线对比Fig.11 Comparison of force-velocity curves between different dampers
计算得到位移响应的峰值与均方根值见表3,可以看出:ECD-RGW 与FVD 均能有效降低结构位移响应.ECD-RGW 可以减少结构39.3%的位移峰值响应,FVD 的结构减震率则随着速度指数α的升高不断减少,即振动控制性能越来越差.同时,附加ECDRGW 的结构减震率非常接近附加FVD 的结构减震率,尤其接近α=0.6 的FVD.图12 给出了单自由度系统的位移响应时程曲线,从图12 可以看出:附加ECD-RGW 和FVD(α=0.6),系统的位移响应时程非常接近.因此,ECD-RGW 可以作为一种替代FVD 且力学性能更优良的新型耗能装置为结构提供有效的减震作用.

图12 位移响应时程曲线Fig.12 Time histories of displacement response

表3 位移响应的峰值与均方根值Tab.3 Peak value and RMS of displacement responses
5 结论
采用数值模拟,对新型齿轮齿条式电涡流阻尼墙ECD-RGW 的阻尼性能进行了研究,分析了主要设计参数对其阻尼特性的影响,得到主要结论如下:
1)ECD-RGW 作为一种安装在建筑结构中的新式墙型阻尼装置,其耗能过程伴随速度放大效应,其力学性能可靠,阻尼参数易调节.
2)在一定范围内减小气隙长度、加装导体板背铁、增大永磁体数量均可显著提高电涡流阻尼墙的电涡流阻尼力和等效阻尼系数.导体板厚度的设计与材料的选取对阻尼力的临界速度影响较大,应考虑阻尼墙的预期工作速度区间.
3)ECD-RGW 能有效降低结构在地震作用下的位移响应,在墙型阻尼器中电涡流阻尼代替黏滞阻尼具有可行性.
