车用磁流变阻尼器的试验及力学建模研究

王 杰，张真忠，王 亮Wang Jie，Zhang Zhenzhong，Wang Liang

车用磁流变阻尼器的试验及力学建模研究

王 杰，张真忠，王 亮
Wang Jie，Zhang Zhenzhong，Wang Liang

（河北石油职业技术大学 汽车工程系，河北 承德 067000）

针对某型号车用磁流变阻尼器进行阻尼特性试验，得到阻尼器的阻尼力在不同工况下与位移、速度的变化曲线。结合Bouc-Wen模型对磁流变阻尼器进行力学建模，推导出模型各参数与加载电流的关系，进而得出电流与阻尼力之间的关系。最后，对比模型仿真结果与试验测试结果，验证磁流变阻尼器的阻尼力可控。

磁流变阻尼器；Bouc-Wen模型；阻尼特性试验；阻尼力

0 引 言

磁流变液是由美国学者J.Rabinow最先发现的一种智能可控的新型材料[1]。当外部没有磁场时，磁流变液与一般的牛顿流体无区别；当外部有磁场时，磁流变液可以在短时间内快速、可逆地由牛顿流体状态变化为固态或类似固态，并且其粘度随着磁感应强度的变化而变化。由于这一过程可逆、可控、迅速，磁流变液常应用于工程制造、减振降噪等领域。磁流变阻尼器是其中一项应用，如图1所示，通过改变通入阻尼器中的电流大小，改变磁流变液所处磁场强度的大小，实现输出阻尼力可控；因此，磁流变阻尼器成为现阶段半主动悬架减振降噪领域的研究热点[2]。

图1 磁流变阻尼器

对某型号车用磁流变阻尼器的阻尼特性进行试验，结合Bouc-Wen模型对阻尼器进行建模。对比仿真结果与试验结果，验证阻尼器输出的阻尼力可控，为后续半主动悬架减振降噪研究提供参考。

1 Bouc-Wen模型

Bouc-Wen模型由Bouc R提出并由Wen Y K等人推导出来，该模型易于数值计算，广泛用于模拟滞回系统[3-4]，其构建思想是将具有滞回特性的磁流变阻尼器理解为弹簧-阻尼结构与滞回系统并联而成的复合系统，如图2所示。

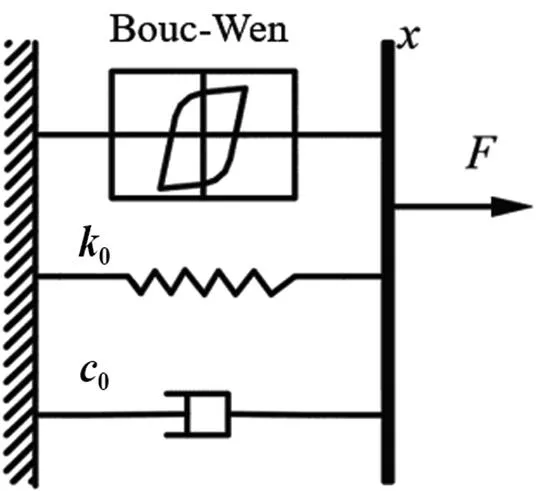
注：F为输出阻尼力；c0为粘滞系数；k0为刚度系数；x为阻尼器的相对位移。

Bouc-Wen模型可以反映输出阻尼力和位移之间的关系，以及输出阻尼力和速度之间的关系，模型公式为

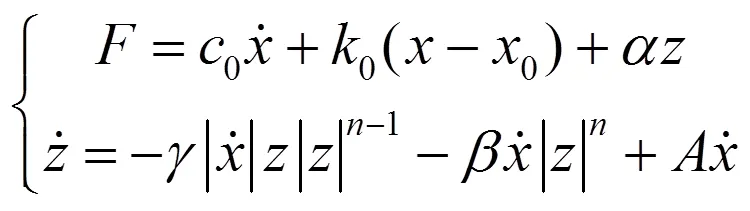
2 阻尼特性试验

现对该车用磁流变阻尼器进行阻尼特性试验，测试该磁流变阻尼器在不同频率、振幅以及加载电流等工况下的输出阻尼力情况。

2.1 试验设备

试验采用英斯特朗E10000型电子动静态万能试验机、直流电源、工装以及电脑等仪器设备进行，如图3所示。

图3 阻尼特性测试系统

磁流变阻尼器的上、下两端由工装固定在试验机上，使磁流变阻尼器在整个试验过程中与试验机保持可靠连接。直流电源控制输入阻尼器中电流大小。万能试验机中的位移传感器和力传感器采集阻尼器出杆的相对位移和阻尼器产生的阻尼力，采集数据最终汇总于电脑中。

2.2 试验工况

选取简谐振动为激励方式，其他试验激励条件为：振幅选取5 mm和10 mm；频率选取0.5 Hz、1 Hz、2 Hz；电流选取0 A、1 A、2 A、3 A、4 A。

2.3 试验结果

根据试验数据绘制阻尼力-位移曲线和阻尼力-速度曲线，如图4、图5所示。

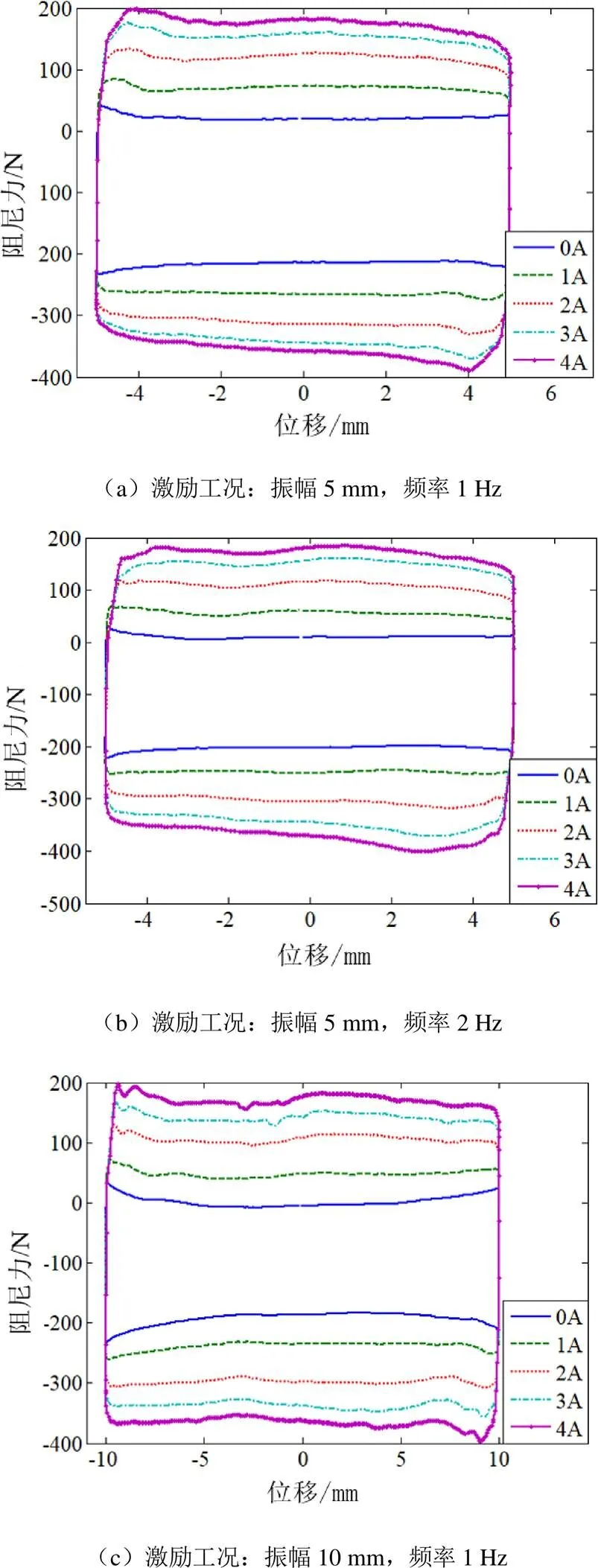
图4 阻尼力-位移曲线

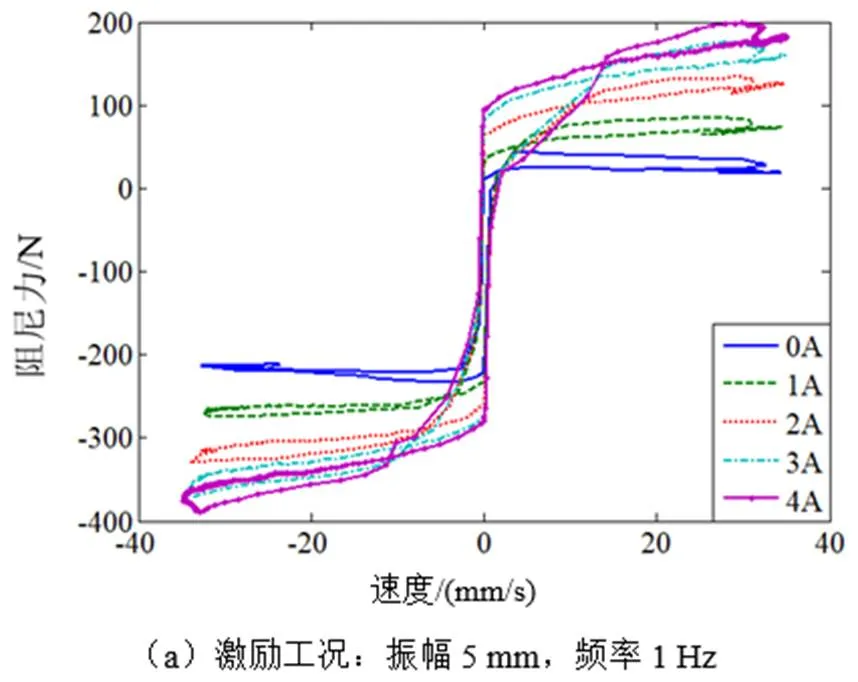
对比图4、图5中不同工况下的曲线发现，当振动激励条件相同时，阻尼力随着加载电流的增大而增大，所围成的面积也逐渐增大，说明阻尼器衰减振动的能力随着电流的增大而变强；在不同的振动激励条件下，各曲线变化趋势相似，说明激励的幅值和频率对磁流变阻尼器的输出阻尼力影响不大。

3 磁流变阻尼器建模

3.1 建模与参数识别

采用式（1）在MATLAB/ Simulink中搭建Bouc-Wen模型，如图6所示。

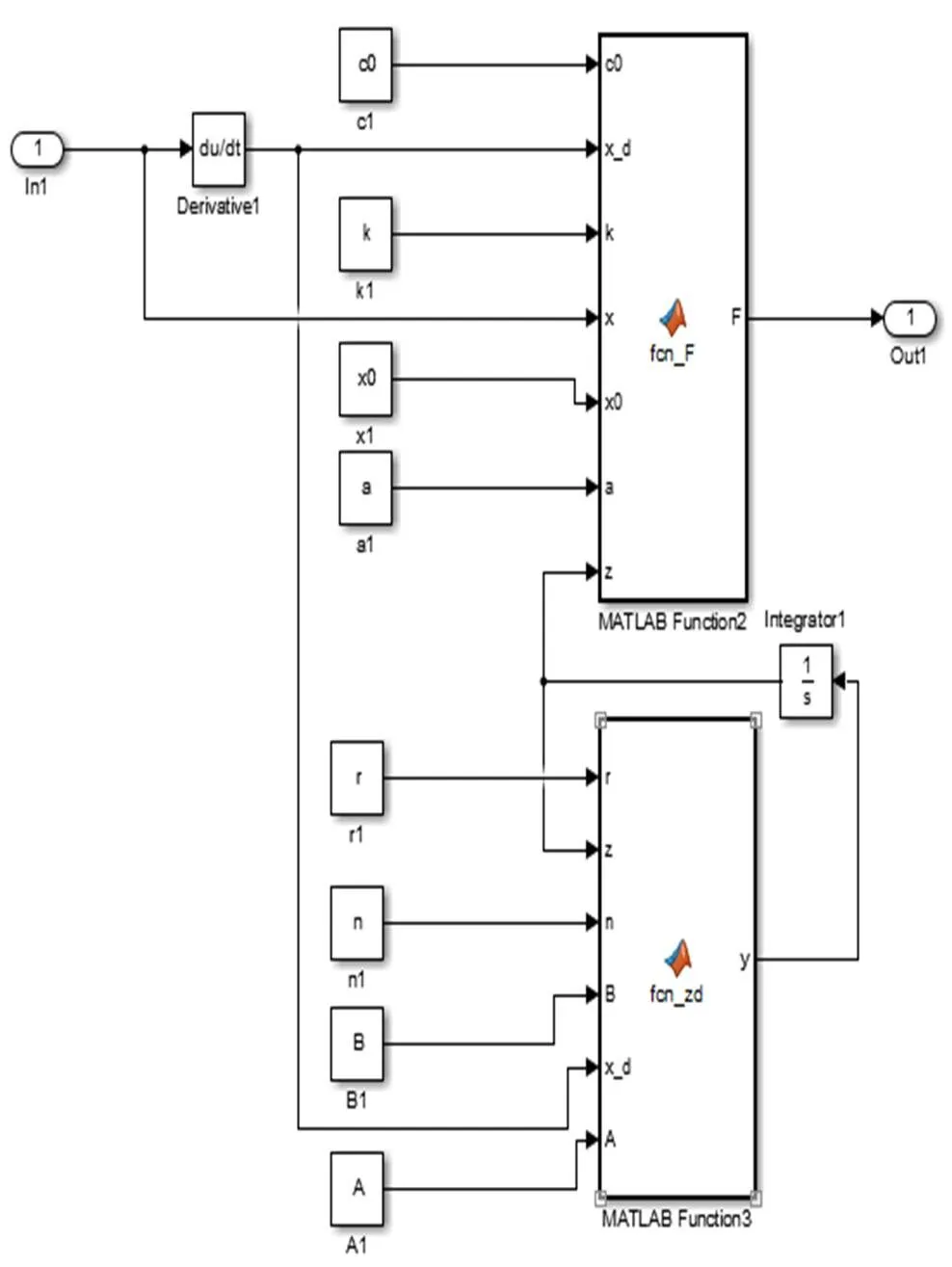
图6 MATLAB中Bouc-Wen模型

将试验所得的位移和阻尼力数据作为Bouc-Wen模型输入（In1）与输出（Out1），采用Simulink的参数估计模块，通过迭代优化进行未知参数识别[5]。

激励工况的幅值和频率对阻尼器的阻尼特性影响不大，选取振幅5 mm和频率1 Hz进行参数识别，将识别后的Bouc-Wen模型的计算拟合值和试验测试值进行对比，如图7所示。

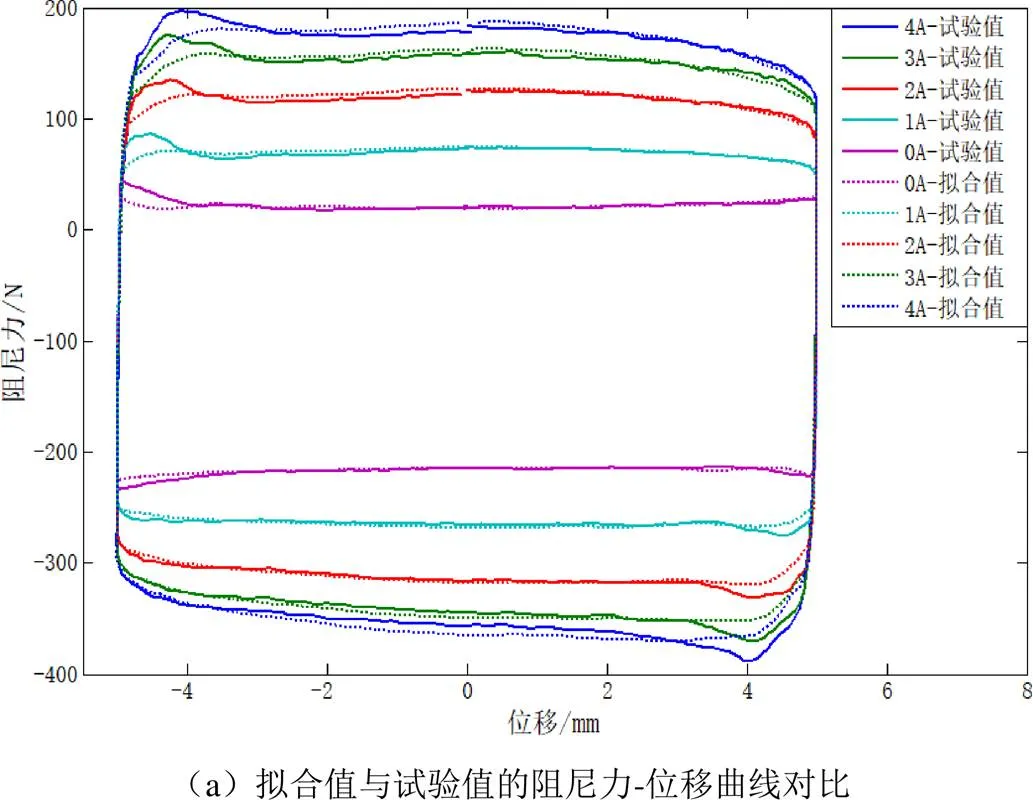
由图7可知，采用Simulink拟合得到的Bouc-Wen模型其数值计算曲线与阻尼特性试验所得曲线基本吻合，参数识别结果满足要求，各参数值为：0=0.627 5，0=0.173 2，0=564.66，其他参数随电流而变化，具体见表1。

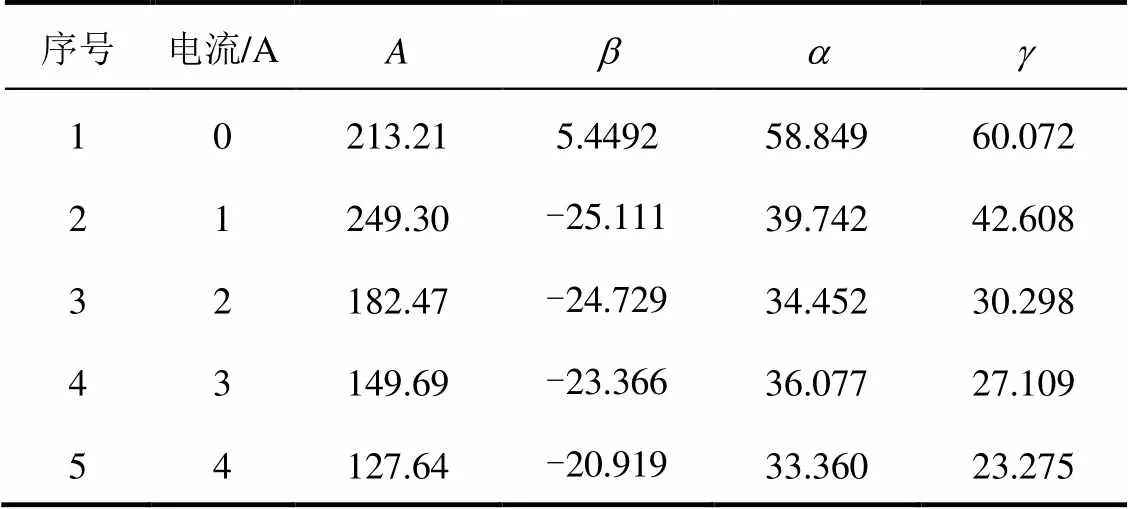
表1 Bouc-Wen模型部分参数

由表1可知，加载电流不同，各参数的识别结果不同，且各参数值呈现一定的变化趋势。采用MATLAB多项式拟合模块，对各参数进行3次多项式拟合，得到

3.2 模型验证

由于Bouc-Wen模型的参数是在振幅5 mm、频率1 Hz的试验条件下识别而来，为验证所建立的模型是否具有通用性，是否在其他的激励条件下也能正确响应，需要将磁流变阻尼器在其他工况下的试验数据输入模型中，进行模型的验证。

如图8所示，将各工况下的试验结果与拟合结果进行对比，发现具有较高的吻合度。其中阻尼力的试验值与拟合值在行程终点差异较大，在运动过程中变化不大。为此分别计算阻尼力为正与阻尼力为负时阻尼力的平均值，以完成模型准确性的验证，具体表2。

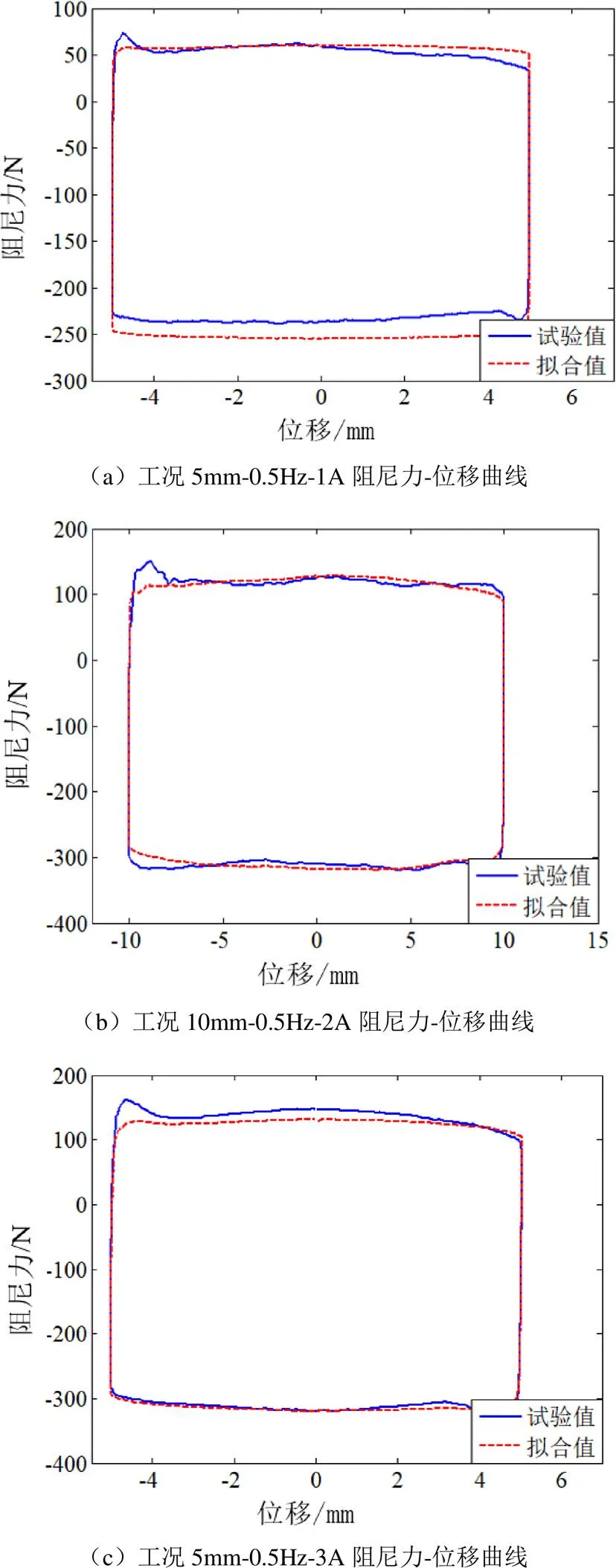
图8 拟合数学模型与试验值的验证对比

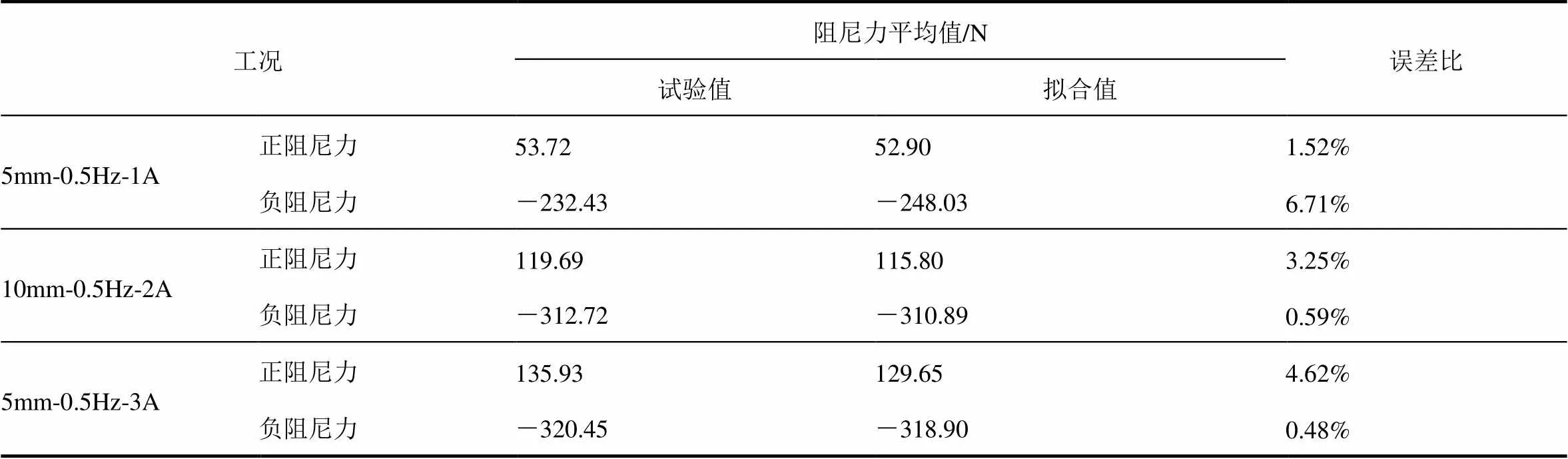
表2 试验值与拟合值对比

由表2可知，拟合值与试验值的误差小于10%， Bouc-Wen模型具有较高的准确度以及很好的通用性，能够较好地拟合阻尼特性曲线，充分证实了磁流变阻尼器阻尼力的可控性。

4 结 论

磁流变阻尼器是目前实现汽车悬架半主动控制的重要装置之一，针对某款车用磁流变阻尼器在试验机上进行阻尼特性试验进行分析，结果表 明磁流变阻尼器工作时，随着加载电流增大，阻尼力峰值以及阻尼力-位移曲线所围成的面积也逐渐增大，说明随着加载电流增大，阻尼器衰减振动的能力逐渐变强。

结合试验数据和Bouc-Wen模型完成磁流变阻尼器建模，拟合出各参数与加载电流之间的关系。通过验证发现，采用Bouc-Wen模型对磁流变阻尼器建模具有较高的准确性和通用性，充分验证了磁流变阻尼器的输出阻尼力可由外加电流进行控制，为后续车辆半主动悬架的开发提供参考。

[1]RABINOW J. The Magnetic Fluid Clutch[J]. Electrical Engineering, 1948, 67(12):1167.

[2]张华良，饶柱石，傅志方，等. 环型极板电流变液可控阻尼器理论建模研究[J]. 振动工程学报，2002，15（1）：31-35.

[3]BOUC R. Modele Mathematique d’Hysteresis[J].Acustica，1971，21.

[4]WEN Y K. Method of Random Vibration of Hysteretic Systems [J].Journal of the Engineering Mechanics Division，1976，102（2）：249-263.

[5]刘中良. 磁流变阻尼器动力学模型的建立和数值模拟研究[D].长沙：中南大学，2012.

2021-08-16

1002-4581（2021）06-0010-05

U463.33+5.1.03

A

10.14175/j.issn.1002-4581.2021.06.003