模态综合法在航天器结构动力学分析中的应用研究

尹家聪，谢伟华，陈 曦，刘 波

(中国空间技术研究院通信卫星事业部，北京100094)

0 引言

部件模态综合法(Component Mode Synthesis， CMS)又简称模态综合法，起源于20世纪50年代初，最早用于计算飞机机翼及整机的固有振动问题。1960年起，Hurty首先确立了模态坐标、模态综合等概念[1]，并逐步发展出以Craig-Bampton为代表的固定界面模态综合法[2]和自由界面模态综合法[3-5]，以及混合界面模态综合法[6-7]等多种方法。Craig在2000年对模态综合法的发展进行了详细综述[8]。

模态综合法具有两大优势和一是可以大幅缩减结构自由度(缩减后的有限元模型称为缩减模型或缩聚模型)，提高计算效率，节约计算成本；二是可以封装产品设计的几何和材料信息，保护企业知识产权。

本文将首先回顾模态综合法在国内外航天器结构动力学分析中的应用现状和模态综合法的基本理论，然后重点研究模态综合法在航天领域结构动力学分析应用中受限的两个问题，即部组件有限元物理模型一级缩聚的接口匹配问题和缩聚/物理混合模型的二级缩聚问题。

1 模态综合法在航天工业中的应用现状

目前，模态综合法已集成到各大结构动力学计算商业软件中，并在航天工业领域得到了广泛应用。例如，NASA在1990年采用MSC. Nastran软件的超单元模态综合分析功能，计算了国际空间站在轨多种动力载荷下的响应特性[9]；MIT在1999年利用詹姆斯韦伯空间望远镜(JWST)的模态综合后的有限元缩聚模型(见图1)，完成了结构-光学-控制一体化的集成建模模型，并进行了初步的微振动分析[10]；21世纪初，国外某公司研制的某卫星，其整星有限元模型也是采用模态综合法进行建模(见图2)，其中星本体采用有限元物理模型建模，而太阳翼、天线等则采用模态综合法得到一级缩聚模型建模。(注：本文中，一级缩聚模型指采用模态综合法，直接由有限元物理模型缩聚得到的模型；缩聚/物理混合模型指将多个一级缩聚模型分别与未缩聚的有限元物理模型装配在一起的混合模型；二级缩聚指将缩聚/物理混合模型再次采用模态综合法进行缩聚，从而把一级缩聚模型未缩减的界面自由度进一步缩减的过程。)

图1 詹姆斯韦伯望远镜的有限元缩聚模型Fig.1 The reduced finite element model of JWST

图2 某卫星有限元缩聚/物理混合模型Fig.2 A hybrid finite element model of a satellite contained both unreduced and reduced sub-structures

图3 我国为巴基斯坦研制的通信卫星的有限元模型[18]Fig.3 The finite element model of a Pakistani telecommunication satellite made by China

我国航天工业部门在20世纪80年代已认识到模态综合法的优势[11]，模态综合法在运载火箭的全箭建模[12]、航天器/火箭的器箭耦合载荷分析[13]、刚柔耦合及全柔性航天器动力学建模[14]，以及大型航天相机[15]、通信卫星[16]、空间站[17]结构动力学分析中均已得到应用。例如在我国在为巴基斯坦研制卫星过程中，在完成卫星动力学分析后，将卫星的有限元物理模型(见图3)采用模态综合法进行一级缩聚，提供给运载方开展耦合载荷分析，预示运载火箭发射过程中的卫星响应，并为卫星地面力学试验条件制定提供参考依据。

总之，模态综合法可以有效解决航天器研制过程中，部组件级、航天器系统级、航天器/运载器大系统级的结构耦合分析问题，但也有一些因素制约了模态综合法在航天器结构动力学分析的工程实践。航天器总体设计部门习惯采用传统有限元物理模型开展动力学分析，模态综合法在组件级、航天器系统级、航天器/火箭大系统级的动力学分析中的应用尚未形成系统，其应用带来的流程变化成熟度也有待提高。

为了拓展模态综合法的工程实践，本文重点研究了模态综合法在应用过程中的两个限制性问题：

1)一级缩聚的接口匹配问题。一些航天器研制过程中，部组件有限元模型越建越细，自由度数目巨大，造成航天器系统结构动力学分析无法计算或计算效率低下，需采用模态综合法对部组件模型进行一级缩聚，以便于航天器系统开展分析。然而，部分部组件模型的建模软件与航天器系统不匹配，使得一级缩聚模型无法有效传递。为此，航天器总体设计部门应研究一级缩聚的接口匹配问题，从而解决和规范部组件缩聚模型的接口。

2)缩聚/物理混合模型的二级缩聚问题。一些航天器与运载的耦合载荷分析，仅针对航天器有限元物理模型的一级缩聚(见图3)，但随着航天器部组件一级缩聚模型的应用，航天器结构动力学分析必然会出现缩聚/物理混合的有限元模型(见图2)。因此航天器总体设计部门应解决缩聚/物理混合模型的二级缩聚问题，从而解决和规范航天器系统和运载的缩聚模型接口。

本文通过Fortran/ Matlab混合编程和采用Nastran DMAP语言二次开发，在一级缩聚的接口匹配和缩聚/物理混合模型的二级缩聚问题上进行了探索，并在航天器型号研制过程中得到了初步应用。

2 模态综合法原理

模态综合法本质上是一种Rayleigh-Ritz降阶方法，即通过把子结构的物理坐标x表示为几种已知部件模态集的线性组合，实现从物理坐标空间到混合界面坐标空间的变换，并缩减子结构的自由度获得缩聚模型。模态综合法的基本原理可通过Majed等于2005年提出的一种剩余柔度混合界面模态综合法(Residual Flexibility Mixed- Boundary Method，RFMB)[7]统一归纳如下：

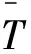
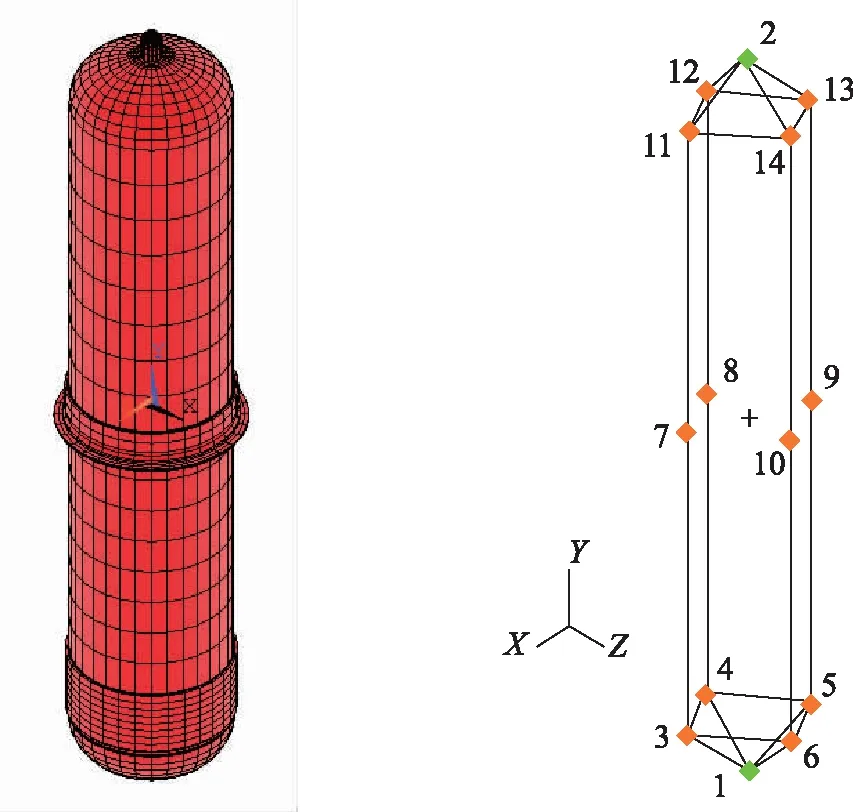
(1)

其中对应于各个模态集的广义坐标用q表示，各模态集的具体计算方法详见Craig的综述[8]。

式(1)可进一步展开写为：

xb=qC

(2a)

(2b)

(2c)

或矩阵形式:

(3)

其中q1表示广义坐标空间。由式(2a)和(2b)可得:

(4)

记qN=qk，那么有q1=T2q2，即:

其中q2表示混合界面坐标空间。

由式(3)和式(5)可得RFMB方法从物理坐标空间到混合界面坐标空间的变换：

x=T1T2q2

(6)

或

(7)

其中，

(8)

(9)

3)另一种常用的混合界面模态综合法(Modified Hintz’s Mixed-Boundary Method, MHMB)，是Hintz’s Mixed-Boundary Method (HMB)[6]的一个改进，其坐标变换可写为:

(11)

该方法是Nastran软件混合界面模态综合法的默认算法[19]。

在工程应用中，一般根据实际需求选择不同的模态综合法：1) 固定界面模态综合法的优点在于原理清晰，算法简单，因此当主要目的在于缩聚子结构的自由度，而无需显示子结构的振动形态时，使用固定界面模态综合法将子结构与其他结构的连接面固支进行自由度缩聚，即可满足工程需求；2) 自由界面模态综合法的优点在于自由边界的子结构模态试验容易实现，模态综合参数易于得到试验验证，因此当需要通过自由边界模态试验修正子结构建模结果时，可以采用自由界面模态综合法；3) 混合界面模态综合法的优点在于既可以充分缩减子结构的自由度，还可以通过轮廓显示单元将缩聚后的固定界面和自由界面点连接起来，以显示子结构的几何轮廓及其在动力载荷下的振动响应，且无需经过数据恢复即可获得自由界面点上的动力响应，缩聚后的模型特别适合于代替子结构的有限元物理模型用于不同设计部门间的模型传递。

3 有限元一级缩聚的接口匹配问题

早在1966年，为了满足航空航天工业对结构分析的需求，NASA就主持开发了商业有限元软件Nastran。经过半个多世纪的发展，Nastran已成为航天工业有限元分析的国际标准。我国各航天器总体部门也多采用Nastran进行航天器有限元建模和结构力学分析。然而，部分航天器部组件研制单位习惯采用ANSYS或其他非Nastran的有限元商业软件进行力学分析；不同软件在使用模态综合法缩聚子结构模型时具有不同的格式，这为部组件一级缩聚模型向航天器系统级的传递带来了困难。

以ANSYS软件建立的部组件有限元模型为例，本文采用如下流程解决一级缩聚的接口匹配问题：1)用ANSYS的HBMAT命令输出部组件模型，以Harwell-Boeing稀疏矩阵格式存储的刚度和质量矩阵，以及结点坐标和自由度编号信息；2) 用Fortran软件编程快速读取ANSYS输出的刚度、质量矩阵，并转换为Matlab可以识别的三元组稀疏矩阵格式；3) 用Matlab读取步骤1、2的输出数据，并用Matlab编程实现Nastran的混合界面模态综合法，生成可以被Nastran识别的一级缩聚模型，包括缩聚后的刚度、质量矩阵，界面自由度和广义自由度的编号信息，界面点的坐标以及轮廓显示单元的定义；4) 用Nastran软件读取一级缩聚模型，并完成其与航天器系统级有限元模型的装配。

作为示例，图4(a)设定了某卫星推进分系统的气瓶ANSYS有限元模型。该模型采用体单元建模，在自由边界条件下大约有5万个结点，1.7万个单元，15万个自由度。通过自编的Fortran/Matlab混合界面模态综合法程序，可以将此ANSYS有限元物理模型一级缩聚为Nastran可识别的缩聚模型，如图4(b)所示。图4(b)中，结点1、2的自由度设置为气瓶在整星安装的固定界面自由度；结点3～14的自由度设置为自由界面自由度。结点1～14通过24个PLOTEL轮廓单元组成气瓶缩聚模型的显示框架。缩聚后的模型仅有104个自由度(包括50个正交模态即k=50)，相对于原模型大幅减少了自由度。

(a)缩聚前ANSYS模型 (b) 缩聚后Nastran模型图4 某气瓶缩聚前后的有限元模型Fig.4 The original ANSYS finite element model of a gas tank (left) and its reduced model in Nastran(right)

表1给出了某气瓶缩聚前后自由边界条件下的固有频率对比结果：其中，前6阶刚体频率虽然由于计算误差不完全为0，但计算结果相近，且缩聚前后前6阶刚体模态在各个自由度方向的模态有效质量百分比之和均为100%。图5给出了某气瓶缩聚前后自由边界下第7阶固有频率的模态振型。由表1和图5可知：缩聚算法正确有效，气瓶的Nastran缩聚模型可以用于航天器整体的有限元建模。

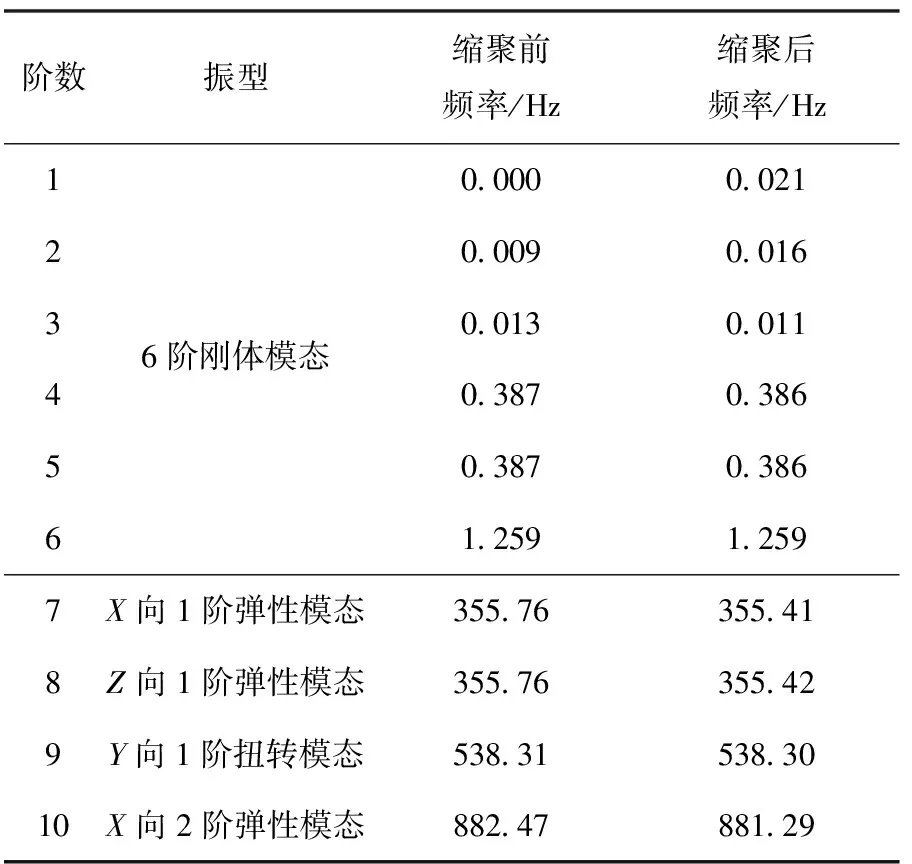
表1 某气瓶缩聚前后自由边界条件下的固有频率对比Tab. 1 Comparison of natural frequencies forthe original and reduced models of a gas tank in free-free boundary condition

图5 某气瓶缩聚前后自由边界下第7阶模态振型对比图Fig.5 Comparison of the 7th modal shapes for the original and reduced models of a gas tank

4 缩聚/物理混合模型的二级缩聚问题

耦合载荷分析(Coupled Load Analysis，CLA)是航天器研制过程中与运载火箭协同开展的一项极为重要的分析工作。流程是：先将航天器的有限元物理模型利用模态综合法缩聚到航天器与火箭的连接界面上；然后将航天器的缩聚模型提供给运载方，由运载方完成航天器模型和火箭模型的装配，并仿真分析出火箭飞行过程中器箭界面处和航天器内部典型位置的动力响应。

本文采用Matlab和Nastran DMAP二次开发语言实现了航天器缩聚/物理有限元混合模型的二级缩聚，并开展了虚拟耦合载荷分析验证。作为示例，图6给出了某卫星缩聚/物理有限元模型，该模型包含1个一级缩聚天线，安装在卫星+Z侧舱板上；其余部组件和星本体结构均为有限元物理模型。使用二级缩聚方案对该模型进行二级缩聚前后的固有频率对比如表2所示；其中缩聚前后，前6阶刚体模态在各个自由度方向的模态有效质量百分比之和均为100%。对比结果显示了二级缩聚方案的正确性。

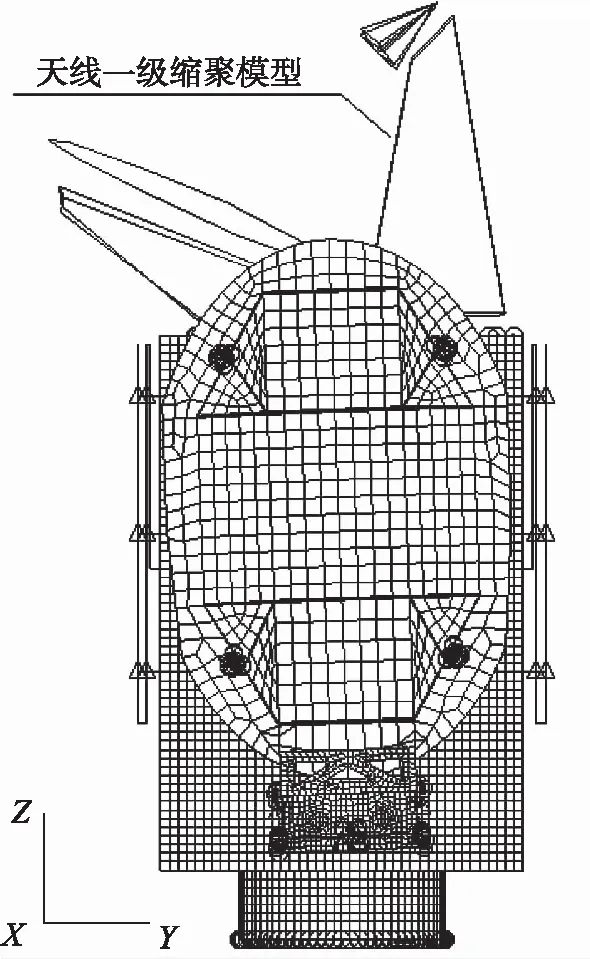
图6 某卫星缩聚/物理混合模型Fig.6 Another hybrid finite element model of a satellite contained both unreduced and reduced sub-structures

为了进一步验证二级缩聚解决方案在CLA中的正确性，把卫星的有限元缩聚/物理混合模型和二级缩聚模型分别装配到一个相同的虚拟火箭模型上，再分别施加相同的虚拟气动力进行虚拟CLA(见图7)以对比分析结果。图8给出了虚拟CLA在星箭界面点X向自由度的典型响应曲线，高度一致的对比结果证明了本文二级缩聚方案的正确性。

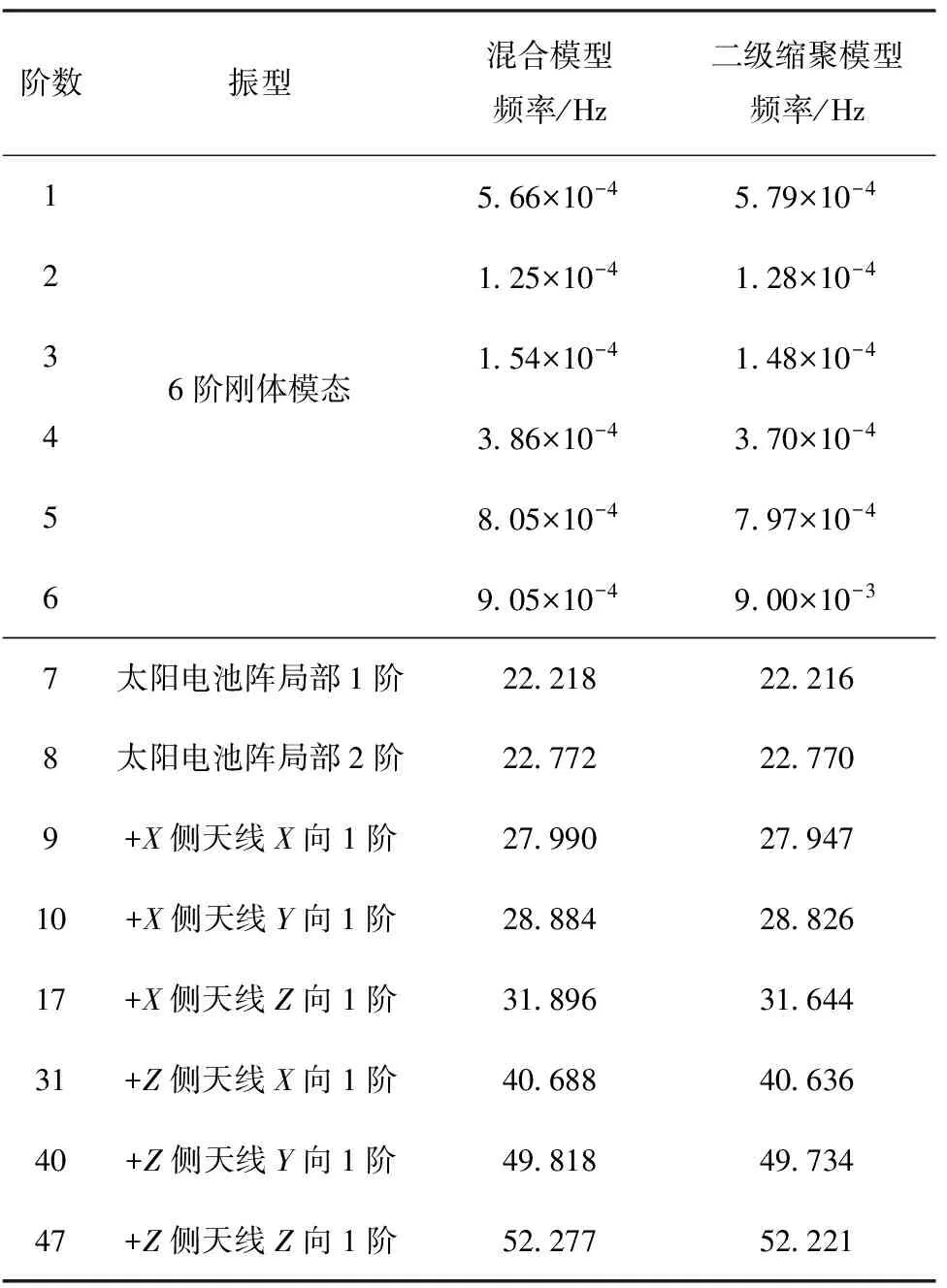
表2 某卫星有限元缩聚/物理混合模型和二级缩聚模型在自由边界条件下的固有频率对比Tab.2 Comparison of natural frequencies for the hybrid satellite model and its second-time reduced model in free-free boundary condition

图7 器箭耦合载荷分析二级缩聚模型的验证示意图Fig.7 A pseudo coupled load analysis for the verification of an obtained second-time reduced model

图8 卫星混合模型和二级缩聚模型的虚拟CLA结果对比Fig.8 Comparison of a pseudo coupled load analysis results for the hybrid satellite model and its second-time reduced model

5 结论

本文简要介绍了模态综合法的基本原理和在国内外航天领域的应用发展，重点研究了模态综合法在航天领域结构动力学分析应用中受限的两个问题：1) 通过采用Fortran/Matlab混合编程实现Nastran的混合界面模态综合法，将ANSYS版本的有限元物理模型直接缩聚为Nastran可识别的一级缩聚模型，从而初步解决了航天器部组件有限元模型的一级缩聚接口匹配问题；2) 通过Matlab和Nastran DMAP二次开发语言，初步解决了包含一级缩聚部组件模型的航天器缩聚/物理混合模型的二级缩聚问题，并通过虚拟耦合载荷分析证明了二级缩聚方案的正确性。相关技术成果可拓宽模态综合法在我国航天器结构动力学分析中的应用范围，并进一步促进我国航天器总体技术设计能力的提高。

[1] Hurty W C. Vibrations of structural systems by component-mode synthesis[J]. Journal of the Engineering Mechanics Division, ASCE, 1960, 86(4)：51-69.

[2] Bampton M C C, Craig R R. Coupling of substructures for dynamic analysis[J]. AIAA Journal, 1968, 6(7)：1313-1319.

[3] Hou S N. Review of model synthesis techniques and a new approach[J]. Shock and Vibration Bulletin, 1969, 40(4)：25-39.

[4] MacNeal R H. A hybrid method of component mode synthesis[J]. Computers & Structures, 1971, 1(4): 581-601.

[5] Rubin S. An improved component-mode representation[J]. AIAA Journal, 1975, 13(8)： 995-1006.

[6] Hintz R M. Analytical methods in component modal synthesis[J]. AIAA Journal, 1975, 13(8)：1007-1016.

[7] Majed A, Henkel E E, Wilson C. Improved method of mixed-boundary component-mode representation for structural dynamic analysis[J]. Journal of Spacecraft and Rockets, 2005, 42(5)：825-831.

[8] CraigJr R R. Coupling of substructures for dynamic analyses: an overview[R]. AIAA 2000-1573, 2000.

[9] Del Basso S, Singh S K, Lindenmoyer A J. A superelement methodology for coupled loads analysis of Space Station Freedom[C]. 31stStructures, Structural Dynamics and Materials Conference, 1990.

[10] DeWeck O L. Integrated modeling and dynamics simulation for the next generation space telescope[D]. Boston：Massachusetts Institute of Technology, 1999.

[11] 冯振兴. 模态综合法在大型、复杂宇航结构振动特性分析中的应用[C]. 第三届全国振动理论及应用学术会议, 1987.

[12] 杜飞平, 谭永华, 陈建华, 等. 航天器子结构模态综合法研究现状及进展[J]. 火箭推进, 2010, 36(3)：39-44.

[13] 邱吉宝, 张正平, 李海波, 等. 动态子结构法在航天工程中的应用研究[J]. 振动工程学报, 2015, 28(4)：510-517.

[14] 史纪鑫, 曲广吉. 可变构型复合柔性结构航天器动力学建模研究[J]. 宇航学报, 2007, 28(1)：130-135.

[15] 贾海涛, 马洪亮, 吴清文, 等. 超单元在大型复杂航天相机结构中的应用[J]. 微计算机信息, 2009, 25(24)：161-163.

[16] 钱志英, 罗文波, 阮剑华. MSC.Nastran子结构法在航天器结构动力学分析中的应用[J]. 航天器工程, 2011, 20(5)：55-60.

[17] 葛东明, 邹元杰, 史纪鑫. 固定界面模态综合法在空间复杂结构系统中的应用研究[C]. 五院航天动力学论坛第二届学术研讨会, 2016.

[18] 马兴瑞, 韩增尧, 等. 卫星与运载火箭力学环境分析方法及试验技术[M]. 北京：科学出版社，2014.

[19] Nastran M S C. Superelement user’s guide[R]. Moscow, MSC Public, 2013.