基于改进禁忌搜索的基站布局优化算法
2018-03-06陈诗军王慧强陈大伟刘秀兵胡海婧
陈诗军,王慧强,陈大伟,刘秀兵,胡海婧
(1.中兴通讯股份有限公司无线预研部,广东 深圳 518055;2.哈尔滨工程大学计算机科学与技术学院,黑龙江 哈尔滨 150001)
1 引言
随着社会的快速发展,人们更多时间是在室内活动,对室内位置服务的需求与日俱增。美国通信委员会的E-911 条例强制性要求公共网络在任何时间、地点,都能通过无线信号追踪到用户的位置[1]。用户对位置服务的需求不断提高。目前GPS、北斗等卫星定位方式的室外定位精度在十几米到几十米之间,而蓝牙、WIFI、UWB(Ultra-Wide Band)定位的使用场景受限,大量研究都认为在即将到来的5G时代,蜂窝网将是室内外一体化定位的首选技术[2]。鉴于室内环境的非视距等诸多特性,基站布局的目的就是在不增加硬件设施成本的同时扩大信号覆盖面积,从而提高定位精度,合理的基站布局显得尤为重要。
基站布局的优化能够大大提高定位终端的定位精度,根据基站选择算法来选择到定位点有首径信号的基站[3],可以缩小定位误差,得到更好的定位精度。
现有的基站布局优化算法主要考虑的是基站的位置和数量对整体网络覆盖范围和信号质量的影响,优化目标是在满足通信网络建设目标的前提下,考虑网络容量、信号覆盖范围、通信质量和成本等因素,形成最优布局,没有考虑用户对室内三维定位的需求。现有基站布局算法可分为两类:一类是基于随机几何的基站布局算法;另一类是基于多目标优化的基站布局智能算法。
在随机几何方面,Andrews[4]首次用齐次泊松点过程建模蜂窝网络的布局,并分析了覆盖率、可达速率这两个性能指标。但是,齐次泊松点过程仍不是一个理想的模型,用该方案建模蜂窝网络中的基站位置则意味着所部署的基站相互间是完全独立的[5]。随着蜂窝网络逐渐向多层异构通信网络的方向进行演变,为了更准确地建模蜂窝网络的站点排布,近年来出现了许多新兴的点过程,例如硬核过程HCP(Hard-Core Processes)[6]、泊松簇过程PCP(Poisson Cluster Process) 以及扰动格型PL(Perturbed Lattice)[7]等等。这些点过程最主要的缺陷就是难以用于分析,限制了它们在无线网络中的进一步应用。
基于多目标优化的基站布局智能算法由于适应性较强,易于建模等优势更为常用,对此国内外学者提出了许多智能算法。文献[8]提出了基于模拟退火SA(Simulated Annealing)算法的解决方案,但模拟退火算法中的“温度”初始值以及下降速率需要重复多次实验才能确定。文献[9]的粒子群算法又称蚁群算法,基于群智能优化的思想,在应用到基站优化问题时,易于修改目标函数,并且可并行实现,可扩展性较优,但由于种群在搜索空间中丢失了较多的多样性信息,易陷入局部最优解。文献[10]提出了基于传统遗传算法GA(Genetic Algorithm)布局方案,引入Pareto最优域,提出了高性能的NSGA-II 算法,该算法属于启发式搜索算法,也易于改写为并行处理版本,但全局搜索能力不强,易陷入局部最优解[11]。
文献[12]为解决WSN(Wireless Sensor Network)中RFID(Radio Frequency IDentification) 定位场景中的读写器布局问题,提出了一种RFID读写器部署算法,该方法基于禁忌搜索算法,考察了读写器布局对定位精度的影响,并结合禁忌搜索策略来寻找最优布局方案,但是没有考虑覆盖区域存在障碍物的情况,如果使用在室内现实情况,定位误差会大大提高。
基于以上研究与分析,本文提出一种改进禁忌搜索算法应用于基站布局优化,该算法基于禁忌搜索模型,迭代更新候选基站布局列表,实现基站布局的局部寻优过程。为验证改进禁忌搜索算法的有效性,该算法与文献[12]提出的RFID读写器布局算法进行了性能对比实验。
2 禁忌搜索模型
禁忌搜索算法与其他智能优化算法的主要区别是利用临时记忆引导算法的搜索过程,它模拟了生物的记忆过程。禁忌搜索算法是在邻域搜索的基础上,通过禁忌规则来解锁一些已禁忌的良好状态,从而确保多种有效搜索,最终实现全局优化。
2.1 邻域搜索
邻域搜索是基于贪心思想,在当前解的邻域中进行搜索,搜索结果受邻域产生规则和初始解的影响较大。邻域搜索过程如下:
(1)给定初始解x0,该解为当前问题的一种可行解;设置当前最优解xbest=x0,根据邻域产生规则,产生当前可选解的集合T=N(xbest),其中N(xbest)为xbest的邻域;之后执行步骤(2)。
(2)当T-xbest=∅,即当前可选解仅包含当前最优解一个元素时,或满足其他停止运算规则(例如最大迭代次数的限制等规则)时,输出当前最优解xbest,停止运算;否则,执行步骤(3)。
(3)从T中选取集合S,并获取S中的最优解作为当前评估解xnow;若f(xnow) 步骤(1)中的初始解可随机生成,也可根据经验或其他算法得到;N(xbest)为xbest的邻域,邻域指的是当前最优解经过一定范围内的变化,形成一组可选解,这种变化称为“移动”,该组解是否可行需要执行后续步骤来判断。步骤(2)中的停止运算规则,一般包括T为空、达到规定最大迭代次数、超过规定最大运行时间等。步骤(3)中的S的集合选取方式较为灵活,S可选取为全部T,也可以只选T中的最优解。S的元素多,则迭代过程中的计算量将增大,但产生的可选解较多;S的元素少,则计算量将减少,但产生的可选解很少。针对问题的不同场景,可采取不同的选择方式。 邻域搜索基于贪心思想,导致搜索结果比较依赖初始解的设置和邻域产生规则,若初始解的代价值过高,或邻域产生的可选范围较小,则最终搜索结果会比较差,搜索过程中易陷入局部最优解。为了实现全局寻优,算法采取“禁止最近已访问解”的禁忌策略,并接受一些次优解,避免在局部最优解中死循环。 禁忌策略是一种“记忆”过程,记录已经进行过的优化过程,加入到禁忌表中。禁忌表中保存了最近迭代过程中已经进行过的“移动”,位于禁忌表中的移动作为禁忌对象,在当前的迭代过程中是不能作为可选解或是最优解被访问的。这种禁忌策略可防止局部最优解的死循环。 为了尽可能达到可产生最优解的移动,禁忌搜索还引入了“解禁策略”。对当前最优解xbest,在其邻域范围内进行移动产生一组可选解,从可选解中选出最优可选解xnow,并将该最优可选解的代价f(xnow) 与best_so_far进行比较,若f(xnow)优于best_so_far,则将xnow解禁,并用xnow替代xbest,f(xnow)替代best_so_far,更新禁忌表中禁忌对象的禁忌长度,然后将xnow加入禁忌表。 如果不存在代价值优于best_so_far的可选解,则从当前可选解中获取未禁忌的最优解,并将该解作为当前解,不与当前最优解进行比较,更新禁忌表中禁忌对象的禁忌长度,然后将该解加入禁忌表。 (1)初始解。 本文中初始解表示初始基站布局,初始基站布局在水平方向呈正六边形“蜂窝”结构均匀分布。在垂直方向上,根据定位场景的空间范围,每一定高度都布局一层这种“蜂窝”结构均匀分布的基站。为防止初始解代价过高,通过执行多次禁忌搜索算法,将上一次得到的优化布局作为下一次禁忌搜索的初始解,从而扩大可选解范围,避免陷入局部最优。 (2)代价函数。 (3)邻域产生规则。 本文中的邻域产生规则是对基站进行各方向上的移动。具体指的是基站三维空间中x,y,z三个坐标轴方向上可进行共计6种方向的单位移动,包括(-1,0,0),(1,0,0),(0,-1,0),(0,1,0),(0,0,-1),(0,0,1),其中0表示对应的坐标值不变,1表示对应的坐标向对应坐标轴正方向移动1个单位距离。 (4)禁忌表。 本文所指的禁忌对象属性如表1所示。 Table 1 Properties of tabu objects 禁忌表记录了最近搜索过程中已出现的解,禁止这些解在近期内重复出现,从而避免陷入局部最优解。在达到一定迭代次数后,禁忌表会依次释放这些禁忌对象,禁忌对象被释放后,可重新参与计算。因此,禁忌表的数据结构设计为一定长度的先进先出队列。禁忌表的属性如表2所示。 Table 2 Attributes of tabu table 解在加入禁忌表时,均需要设置禁忌长度。在解加入禁忌表的同时,需要为其初始化禁忌长度,并记录加入禁忌表时该解的代价值,算法每次操作禁忌表(加入禁忌对象、解禁禁忌对象)时,将更新一次禁忌表已有元素,已有元素的禁忌长度自动减1,当元素的禁忌长度为0时,将自动从禁忌表中移除。 (5)解禁规则。 在本文中,解禁规则考虑了适配值以及搜索方向两种因素,当优于best_so_far状态的可选解已被禁忌时,解禁此可选解,并将best_so_far状态替换为该可选解。否则若所有可选解均被解禁,也不存在优于best_so_far的可选解,则选择代价值对比禁忌表中代价值有所降低的可选解进行解禁;否则若不存在代价已降低的可选解,则在禁忌表中找到代价最低的解进行解禁。 (6)终止规则。 终止规则用来判断算法是否可结束。本文中终止规则定为达到指定最大迭代次数。 (7)重复初始化。 每一次执行算法时,初始布局是前一次产生的最优布局。在很多情况下,重新初始化后产生的可选解空间将与上一次的可选解空间不同,因此能够更好地避免陷入局部最优解。 (1)选定一个初始基站布局方案,并设定最大迭代次数、定位区域、定位请求次数request_num、基站单位移动距离move_dis、已计算布局队列最大长度H_length,当前迭代次数初始化为0,已计算布局队列H初始化为空。初始基站布局中,在水平方向平面上各个基站呈正六边形“蜂窝”结构,使定位区域包含在基站的覆盖范围内。根据基站数量不同,初始基站布局示例如图1所示。 Figure 1 Example of an initial base station placement scenario图1 初始基站布局方案示例 根据室内三维定位需要,还另需要至少一层水平方向平面上的基站,这些基站同样在水平方向平面上呈正六边形“蜂窝”结构。 当前初始基站布局方案记为x0,记当前最优布局为xbest=x0,并根据当前最优布局产生可移动布局N(xbest),候选布局队列T=N(xbest),其中N(xbest)表示xbest的可移动布局。基站可在三维空间中x,y,z三个坐标轴上进行共计6种方向的单位移动,包括(-1,0,0),(1,0,0),(0,-1,0),(0,1,0),(0,0,-1),(0,0,1),其中0表示对应的坐标值不变,1表示对应的坐标向对应坐标轴正方向移动1单位距离move_dis,-1表示对应的坐标向对应的坐标轴负方向移动1单位距离move_dis。 (2)从候选布局队列中取出最优布局方案,并将最优布局方案从候选布局队列中删除。最优布局方案指的是在候选布局队列中,产生的定位结果平均定位误差最小的方案,即为各基站的三维坐标,记为xnow。平均定位误差指的是在request_num次定位请求中,待定位节点定位结果与真实坐标的欧氏距离的平均值,记xnow的平均定位误差为f(xnow) 。此时若达到最大迭代次数,或候选布局队列为空时,输出当前最优布局,停止运算;否则,转(3)。 (3)考察候选布局队列中最优的布局方案xnow的误差,若f(xnow) 为验证ITSA(Improved Tabu Search Algorithm)算法的有效性,并评估其性能,本文利用MatLab模拟室内场景对基站布局优化算法进行仿真,测试其功能,并与现有的基站布局算法进行对比,验证ITSA算法的性能。 验证基站布局优化算法的仿真场景如图2所示,室内环境为两层,每层房间总长度为15.8 m,宽度为6.4 m,高度为6.3 m。设置墙体厚度为0.2 m,地板与天花板的厚度为0.1 m。其中,设置每个房间的长为5 m,宽为6 m,高为3 m。基站布置12个,分为两层布局,每层数量为6个。内层基站之间的距离25 m,内层和外层对应基站的距离同样为25 m。 Figure 2 Positioning the simulation scenario图2 定位仿真场景 (1) 验证ITSA算法的有效性。比较基站布局优化算法前、改进禁忌搜索算法和RFID读写器布局算法优化后的数据,分析室内三维定位算法的定位结果优化情况,并根据实验所得的定位误差统计结果进行分析。 (2) 考察ITSA算法的性能。将本文提出的基站布局优化算法与文献[12]提出的RFID读写器部署算法进行性能对比,并根据实验所得的几何精度因子GDOP(Geometric Dilution Precision)[13]特征值对定位结果进行分析。 实验1验证ITSA算法的有效性。 按照4.1节中介绍的定位场景,设定位区域为基站覆盖的房屋内部,根据房屋的空间限制,设置用户设备的可移动范围为x轴0.2~15 m,y轴0.2~6 m,z轴0.2~6 m。默认测距信息噪声服从均值为0,方差为1的高斯分布,比较基站布局优化算法前和使用两种优化算法后的结果,随机抽取定位区域中的10 000个点进行定位,得到的定位误差统计结果如图3所示。 Figure 3 Statistics of positioning error 图3 定位误差统计结果 由图3可知,基站布局优化前得到的定位结果均大部分处于1.5~2 m的误差范围,但在基站优化前,有34.15%的定位结果处于2~2.5 m的误差范围内,且处于1~1.5 m的较小误差范围内的定位结果仅占12.39%;经过ITSA算法优化后,1~1.5 m误差范围内的定位结果比例提高了28.6%,相比RFID读写器布局算法提高了9.09%,2.5~3 m的较大误差范围内的定位结果比例降低了17.65%。 进行10 000次基站布局优化定位算法,基站布局优化前、ITSA算法优化后和RFID读写器布局算法的定位算法统计特征值如表3所示。 Table 3 Statistical features of the positioning algorithm 实验2考察ITSA算法的性能。 Figure 4 Statistics of placement optimization results 图4 布局优化结果统计 图4中,圆点表示基站,上三角点表示对应位置的GDOP值在1.2以下,方块点表示GDOP值在1.2~1.3,下三角点表示GDOP在1.3~1.4,六芒星点表示GDOP值在1.4以上。对比三种布局,GDOP值的分布情况总结如表4所示。 由表4可知,相比RFID读写器部署优化算法,本文提出的布局优化算法整体降低了GDOP值,与优化前的布局相比,GDOP≤1.2的比例提升了1.3%,GDOP>1.4的比例降低了2.13%;与RFID读写器部署优化算法相比,GDOP≤1.2的比例提升了0.1%,GDOP>1.4的比例降低了6.7%,说明ITSA算法能够较好地提升定位效果。 Table 4 GDOP positioning algorithm statistical features 本文提出的一种改进禁忌搜索的基站布局优化算法,改进了代价函数、邻域产生规则和解禁规则。在相同的室内场景中,通过仿真实验,相比RFID读写器部署优化算法,该算法能够更好地降低定位区域的整体误差。ITSA算法对定位算法进行基站布局优化后,2.5~3 m的较大误差范围内的定位结果比例降低了17.65%。 [1] Xie Dai-jun. Research on indoor localization technology of wireless local area network[D].Zhengzhou:People’s Liberation Army Information Engineering University,2013:22-30.(in Chinese) [2] Zhou Y F, Zhao Z F, Zhang H G. Towards 5G:Heterogeneous cellular network architecture design based on intelligent SDN paradigm[J].Telecommunications Science,2016,32(6):28. [3] Liu J,Yang Q,Simon G.Optimal and practical algorithms for implementing wireless CDN based on base stations[C]∥Proc of 2016 IEEE 83rd Vehicular Technology Conference (VTC Spring),2016:article 331,1-5. [4] Andrews J G, Baccelli F, Ganti R K. A tractable approach to coverage and rate in cellular networks[J]. IEEE Transactions on Communications, 2011, 59(11): 3122-3134. [5] Andrews J G,Gupta A K,Dhillon H S.A primer on cellular network analysis using stochastic geometry[J].arXiv preprint arXiv:1604.03183v2,2016. [6] Chen M,Hu Y,Yin C.Tri-sectoring and power allocation of macro base stations in heterogeneous cellular networks with Matern Hard-Core Processes[C]∥Proc of 2016 IEEE 83rd Vehicular Technology Conference (VTC Spring),2016:article 461,1-5. [7] Banani S A,Adve R S,Eckford A W.A perturbed hexagonal lattice to model base station locations in real-world cellular networks[C]∥Proc of Globecom Workshops (GC Wkshps),2015:1-6. [8] Zhang H,Zhang S,Bu W.A clustering routing protocol for energy balance of wireless sensor network based on simulated annealing and genetic algorithm[J].International Journal of Hybrid Information Technology,2014,7(2):71-82. [9] Pereira M B,Cavalcanti F R P,Maciel T F.Particle swarm optimization for base station placement[C]∥Proc of the 2014 International Conference on Telecommunications Symposium (ITS),2014:1-5. [10] Meng H,Long F,Guo L,et al.Cooperrating base station location optimization using genetic algorithm[C]∥Proc of 2016 IEEE Conference on Control and Decision(CCDC),2016:4820-4824. [11] Deng Na.Modeling and design of heterogeneous cellular networks based on random geometry[D].Hefei:China University of Science and Technology,2015:21-29.(in Chinese) [12] Wang Yong-hua, Yang Jian,Zhan Yi-ju, et al. RFID networks planning based on tabu search algorithms[J]. Application Research of Computers,2011,28(6):2116-2119.(in Chinese) [13] Feng G,Shen C,Long C,et al.GDOP index in UWB indoor location system experiment[C]∥Proc of SENSORS’15,2015:1-4. 附中文参考文献: [1] 谢代军.无线局域网室内定位技术研究[D].郑州:解放军信息工程大学,2013:22-30. [11] 邓娜.基于随机几何的异构蜂窝网建模分析与设计[D].合肥:中国科学技术大学,2015:21-29. [12] 王永华,杨健,詹宜巨,等.一种基于禁忌搜索的 RFID 读写器部署算法[J].计算机应用研究,2011,28(6):2116-2119.2.2 禁忌与解禁策略
3 改进禁忌搜索的基站布局优化算法
3.1 参数设计



3.2 算法设计

4 算法仿真结果
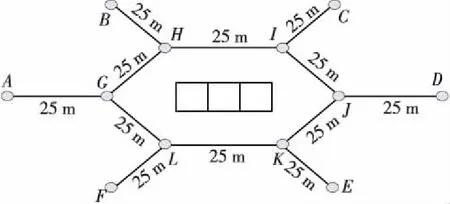
4.1 仿真场景设置
4.2 实验目的
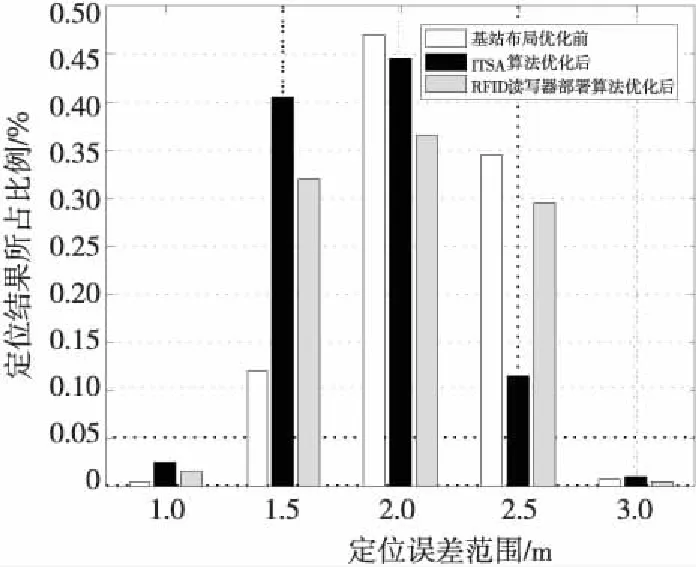
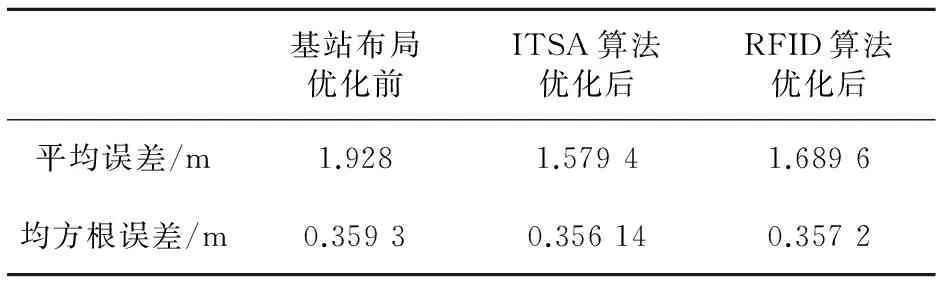
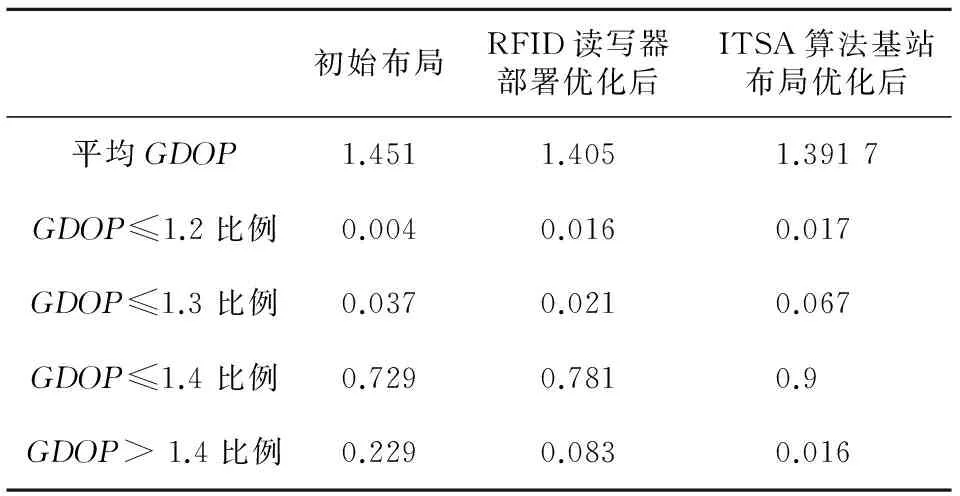
4.3 仿真实验分析
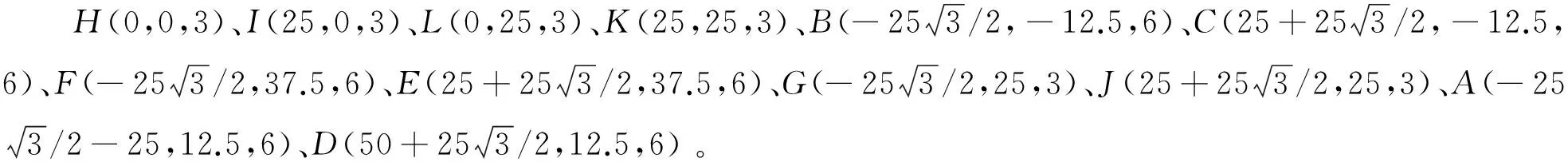

5 结束语
