改进的模糊聚类在控制系统故障诊断中的应用

王印松，商丹丹，王艳飞，张婉君

(华北电力大学控制与计算机工程学院，河北 保定 071000)

1 引言

随着科学技术的不断推进，现代控制系统的规模逐渐大型化，复杂程度也日益增大。为了提高控制系统的安全性和可靠性，需要对整个系统的运行状态进行监控，及时发现系统的故障信息，进而采取相应的措施，防止灾难性事故的发生。因此，控制系统的故障诊断技术是一项很具有实际意义的研究课题，引起了大批学者的广泛关注[1]。

众所周知，控制系统一旦发生故障，其运行参数表现出的特性会与正常状态有所不同，因此这些差异蕴含了系统的故障信息。国内外众多学者通过利用这些故障信息提出了不同的诊断方法。文献[2,3]提出了基于模型匹配的方法进行故障诊断，但这种方法几乎都是在线性模型下实现诊断的，具有很大的局限性。文献[4，5]提出了基于机器学习和先验知识的故障诊断方法。这种方法适合于可以获取大量经验和知识的场合，但当过程所反映的经验和相关知识难以得到时，其诊断结果的准确性将受到很大影响。近些年来，基于数据驱动的方法[6 - 8]在控制系统故障诊断领域已成为一大研究热点。聚类分析[9,10]作为数据驱动的方法之一，在处理大量相关数据时有着其他方法不可比拟的优点。聚类分析是一种无监督的学习，根据样本的相似性进行分类，使处于同一类的样本具有较大的相似性，而处于不同类的样本则差异性较大。

但是，聚类算法自身也具有一定的缺点，聚类中心易受到样本分布的影响。针对聚类算法对噪声敏感这一现象，利用小波分析对实际采集到的数据进行处理，提取故障特征，降低噪声的影响。且传统的模糊聚类算法仅利用了故障数据集的数值特征信息，却忽略了样本矢量间对聚类结果的影响。因此，针对上述问题，本文提出了采用高斯密度函数作为加权系数的模糊C-均值聚类算法。最后，将该算法应用到控制系统中进行故障诊断，验证了该算法的有效性和可行性。

2 改进模糊C-均值聚类算法

2.1 模糊C-均值聚类算法

模糊C-均值聚类FCM(Fuzzy C-Means)[11,12]算法是目前应用最广泛的一种模糊聚类算法。FCM聚类算法的基本思路是通过将待测样本集分成c类，各个样本以不同的隶属度隶属于c个数据中心，通过不断循环计算修改隶属度矩阵和聚类中心矩阵，实现动态迭代聚类，以实现目标函数最小的目的。

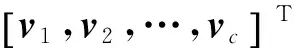
用dik表示单个数据样本与聚类中心的欧氏距离，则:

(1)

FCM算法目标函数为:

(2)

其中，m表示权重指数，m∈[1,+∞)；J(U,V)表示c个类中的数据样本到每个聚类中心的距离平方和，J(U,V)取得的值越小，则说明聚类效果越好。当J(U,V)取得最小值时，得到该算法的聚类中心和隶属度分别为：

(3)

(4)

2.2 加权模糊C-均值聚类算法

传统的FCM算法将每个样本对聚类结果的贡献程度看成是一样的，但实际上，每个样本的周围空间密度对聚类中心都会有一定的影响，进而产生不同的聚类效果。对于样本较多的数据集，样本分布越均匀，聚类的效果越好，相反，样本中那些分散的或孤立的点会使得聚类效果变差[13]。因此，针对上述情况，本文提出了一种加权的FCM算法。利用高斯密度函数作为加权系数，不仅充分利用了数据集的本身分布特性，同时高斯密度函数反映样本点的聚集情况，作为加权系数更能反映样本点的实际分布情况。

一般情况下，一个数据集的数据点分布是不均匀的。通常可以用一个数学函数来形式化地模拟每个数据点的影响，它表征了一个数据点在该区域的影响，被称为影响函数[14]。考虑一个数据点所在区的分布密度，其周围的数据点密集程度越高，则说明该数据点的影响函数值越大；反之，则说明该数据点的影响函数值越小。

定义1(聚类对象的密度) 已知数据样本集合X={x1,x2,…,xn}，数据空间的整体密度可以被模型化为所有数据点的影响函数的总和。其中，数据对象xk的密度记作density(xk)，即:

(5)

对其进行归一化可得:

(6)

根据上述分析，得到基于密度函数加权模糊C-均值聚类DFCM(Density function based FCM)算法的目标函数为：

(7)

在DFCM算法的目标函数下，其迭代步骤是：

步骤1给定聚类中心数目c(2≤c≤n，n表示样本个数)和迭代终止误差ε，初始化迭代次数b=0及隶属度矩阵U(0)。

步骤2根据公式(6)计算样本的权值wk,k=1,2,…,n。

步骤3用如下公式更新聚类中心P(b)。

(8)

步骤4用如下公式更新隶属度矩阵U(b+1)。

(9)

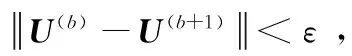
加权系数wk主要用于聚类中心的调整，当wk=1/n时,即认为样本中的各个数据点对聚类的贡献程度是一样的，此时DFCM算法就转变为经典的FCM算法。

3 仿真验证

3.1 基于改进模糊聚类算法的故障诊断步骤

将DFCM算法应用到控制系统传感器与执行器的故障诊断研究中。其诊断步骤如下：

步骤1获取实验数据：搭建水箱控制系统的故障模型，进行故障数据采集；

步骤2数据处理：利用小波分析对数据进行降噪处理，然后通过均值化方法使得数据无量纲化；

步骤3故障诊断：利用DFCM算法对故障进行分类识别。

诊断方法的步骤示意图如图1所示。

Figure 1 Flow chart of diagnosis based on the DFCM图1 基于DFCM诊断流程图

3.2 获取实验数据

为了验证该算法的有效性，选用了浙江高联科技开发有限公司的PCS-B型过程控制综合实验装置作为控制系统。该系统由上水箱、电动调节阀、液位变送器和控制器等组成。其中，上水箱的液位值通过液位变送器获得，其进水量通过电动调节阀进行调节，电动阀门的开度则由控制器的输出量进行控制。

本文研究的诊断方法主要针对的是控制系统中的传感器与执行器。模拟控制系统常见的故障，其故障模型如图2所示。

Figure 2 Fault model图2 故障模型

以水箱的液位单回路控制系统为研究对象，选取上水箱液位、阀门开度信号、控制器输出信号、超调量、响应时间作为控制系统的故障特征。当系统处于正常状态时，采集控制系统平稳运行时的200个样本作为训练数据；模拟故障状态时，系统开始运行处于正常状态，平稳运行后加入故障(即前100个点为正常样本)，共采集系统的300个点作为待测样本。设定4种故障，如表1所示。

Table 1 Sets of fault

3.3 故障诊断

(1)故障特征提取。

将采集到的故障信号进行小波分解[15]，选取db3小波对信号进行小波变换，然后选用5层小波分解并用第5层重构信号，这是由于考虑到噪声的小波变换系数模值随着尺度的增大而减小，选择层次较高一点的小波重构可以有效减小噪声的影响。

(2)数据均值化。

利用小波分析虽然降低了噪声的影响，但是获得的故障特征在数值上仍存在较大差异，所以必须对数据进行无量纲化处理。这里采用均值化的无量纲处理方法，这样既消除了故障特征在量纲和数量级上的影响，又保留了它们取值差异程度上的信息。

(3)聚类。

通过DFCM算法，对训练样本进行聚类分析，确定其聚类中心。然后计算待测故障样本到聚类中心的欧氏距离，得到最终的诊断结果。

DFCM算法参数的选取如下：权重指数m=2，最大迭代次数设为100，最大允许误差为0.000 1。在Matlab实验平台下，得到4种故障样本的聚类中心,如表2所示。

Table 2 Center of clustering

为了验证所提出的DFCM算法的优越性，选取4种故障下的30组测试样本数据，并在相同参数下进行FCM和DFCM方法故障诊断和测试。两种方法下得到的目标函数随迭代次数变化曲线如图3所示。

Figure 3 Curves of object functions图3 目标函数曲线

由图3可见，在故障数据及设置参数相同的条件下，DFCM算法迭代3步，而FCM算法则迭代6步。这说明DFCM算法与FCM相比，具有更好的收敛性。

训练和测试结果如表3～表6所示。

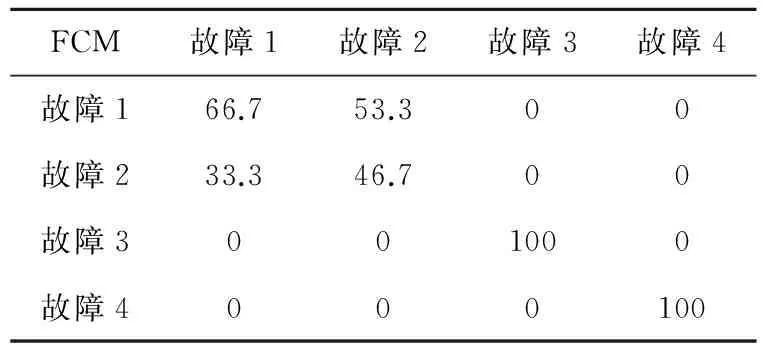
Table 3 Results of the FCM without wavelet analysis

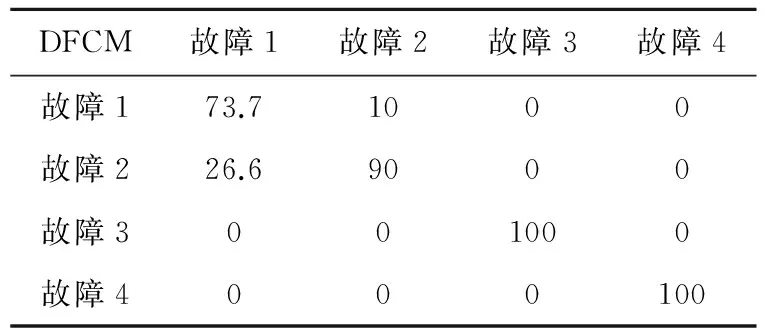
Table 4 Results of the DFCM without wavelet analysis

Table 5 Results of the DFCM with wavelet analysis

Table 6 Comparison of algorithms

由表3和表4可见，在两种算法不加小波分析的情况下，FCM对于传感器和执行器部件之间的故障能准确地区分开，但是具体到区分同一部件的不同故障时，此方法的诊断率较低，由表6可见，它的准确率只有78.35%；而DFCM算法的准确率却有较明显的提高。FCM算法对故障数据进行聚类，其效果差的原因在于它对所有的故障数据均采用相同尺度的处理方法，忽略了样本矢量间对聚类结果的影响。由表5可见，在加上小波分析后，DFCM算法的准确率有了更进一步的提高，说明小波分析对故障特征的提取具有更好的区分性。

通过实验分析，加入小波分析后DFCM算法方法的准确率明显高于未加小波分析的FCM、DFCM算法。因此，提出的小波分析与DFCM相结合的方法提高了控制系统故障的诊断准确率，减少了误判的可能性。

4 结束语

针对控制系统单回路的运行特点，选取对聚类有利的故障特征，并利用小波分析对故障数据进行特征提取，最后通过DFCM算法，对故障进行诊断分类。将该算法与未加小波分析的FCM算法及DFCM算法进行比较，得到如下结论：

(1)小波分析是一种很好的特征提取方法，能有效地降低噪声的影响。

(2)DFCM算法的收敛速度快于FCM算法。DFCM算法通过分配给样本不同的权重值，优化了聚类中心。

(3)小波分析与DFCM算法相结合不仅可以有效诊断出控制系统中传感器与执行器部件之间的故障，还可以对同一部件的不同类型的故障进行诊断。

[1] Zhou Dong-hua,Liu Yang,He Xiao.Review on fault diagnosis techniques for closed-loop system[J].Acta Automatica Sinica,2013,39(11):1933-1943.(in Chinese)

[2] Seron M M, Dona J A D.Actuator fault tolerant multi-controller scheme using set separation based diagnosis[J].International Journal of Control,2010,83(11):2328-2339.

[3] Li Xiao-jian,Yang Guang-hong.Adaptive fault detection and isolation approach for actuator stuck faults in closed-loop systems[J].International Journal of Control,Automation,and Systems,2012,10(4):830-834.

[4] Huo Bao-yu,Tong Shao-chen,Li Yong-ming.Observer-based adaptive fuzzy fault-tolerant output feedback control of uncertain nonlinear systems with actuator faults[J].International Journal of Control Automation and Systems,2012,10(6):1119-1128.

[5] Tian En-gang, Yue Dong.ReliableH∞filter design for T-S fuzzy model-based networked control systems with random sensor failure[J].International Journal of Robust and Nonlinear Control,2013,23(1):15-32.

[6] Goharrizi A Y,Sepehri N.Internal leakage detection in hydraulic actuators using empirical mode decomposition and Hilbert spectrum[J].IEEE Transactions on Instruments and Measurement,2012,61(2):368-378.

[7] Ajami A,Daneshvar M.Data driven approach for fault detection and diagnosis of turbine in thermal power plant using Independent Component Analysis(ICA)[J].Electrical Power and Energy System,2011,43(1):728-735.

[8] Yang Ying-hua,Wei Yu-long,Li Zhao,et al.Process monitoring and fault diagnosis based on subspace mixed similarity[J].Chinese Journal of Scientific Instrument,2013,34(4):935-941.(in Chinese)

[9] Yiakopoulos C T,Gryllias K C,Antoniadis I A.Rolling element bearing fault detection in industrial environments based on a K-means clustering approach[J].Expert Systems with Applications,2011,38(3):2888-2911.

[10] Eslamloueyan R. Designing a hierarchical neural network based on fuzzy clustering for fault diagnosis of the Tennessee-Eastman process[J].Applied Soft Computing,2011,11(1):1407-1415.

[11] Bezdek J C. Pattern recognition with fuzzy objective function algorithms[M].New York:Plenum Pres,1981:637-641.

[12] Jiang Ling-li,Cao Yu-xiang,Deng Zong-qun.Autoregressive parameters estimation based on higher order cumulant as features combining with fuzzy cluster analysis for fault diagnosis[J].Journal of Electronic Measurement and Instrument,2012,26(9):812-817.(in Chinese)

[13] Huang Wei-chun,Liu Jian-lin,Xiong Li-yan.A sample-feature weighted possibilistic fuzzy kernel clustering algorithm[J].Computer Engineering & Science.2014,36(1):169-175.(in Chinese)

[14] Meng Hai-dong,Ma Na-na,Song Yu-chen,et al.Research on fuzzy C-means clustering algorithm based on density function weighted[J].Computer Engineering and Applications,2012,48(27):123-127.(in Chinese)

[15] Cui Bao-zhen,Wang Ze-bing,Pan Hong-xia.Rolling bearing fault diagnosis method based on wavelet applications and fuzzy clustering[J].Journal of Vibration,Measurement & Diagnosis,2008,28(2):151-154.(in Chinese)

附中文参考文献：

[1] 周东华，刘洋，何潇.闭环系统故障诊断技术综述[J].自动化学报,2013,39(11):1933-1943.

[8] 杨英华，魏玉龙，李召，等.基于子空间混合相似度的过程监测与故障诊断[J].仪器仪表学报,2013,34(4):935-941.

[12] 蒋玲莉，曹宇翔，邓宗群.基于高阶累积量的AR参数-模糊聚类法及应用[J].电子测量与仪器学报,2012,26(9):812-817.

[13] 黄卫春，刘建林，熊李艳.基于样本-特征加权的可能性模糊核聚类算法[J].计算机工程与科学,2014,36(1):169-175.

[14] 孟海东，马娜娜，宋宇辰，等.基于密度函数加权的模糊C均值聚类算法研究[J].计算机工程与应用,2012,48(27):123-127.

[15] 崔宝珍，王泽兵，潘宏侠.小波分析-模糊聚类法用于滚动轴承故障诊断[J].振动、测试与诊断,2008,28(2):151-154.