一种基于全局和局部特征匹配的流形对齐算法

徐 猛，王 靖

(华侨大学计算机科学与技术学院，福建 厦门 361021)

1 引言

随着科学技术的飞速发展，现实中所获取、存储和需要处理的数据往往以非结构化的形式存在于高维观察空间中，如高分辨率图像数据、金融统计数据、视频音频数据、全球气候数据及网络文本数据等。这些数据不仅数据量庞大，而且更新速度快。因此，它们的内在规律往往难以直接观察和学习，使得原有的机器学习[1]算法很难对这些数据进行有效的处理。

如何在保持信息完整的情况下从大量数据中提取有效信息，发现其内在规律，一直是模式识别和机器学习研究的热点问题。

近年来，流形学习[2,3]在高维数据降维和数据可视化方面取得了巨大成功。这些算法包括等距映射算法(Isomap)[4]、局部线性嵌入算法LLE(Locally Linear Embedding)[5]、局部切空间排列算法LTSA(Local Tangent Space Alignment)[6]、拉普拉斯特征映射LE(Laplacian Eigen maps)[7]等。尽管这些流形学习算法在机器学习、模式识别、计算机视觉等领域得到了广泛应用，但是只能学习分布于单个流形数据的非线性特征。在现实世界的许多应用中，如跨语言信息检索[8 - 10]、姿态估计[11]、图像和文本的匹配[12]等，数据分布于多个不同流形，需要同时学习两个或者更多的数据集的非线性特征。此时，传统的流形学习算法并不适用。

为了解决这个问题，近年来学者们提出了流形对齐算法[13 - 15]。多数流形对齐算法首先学习每个流形数据集的局部几何结构，如局部近邻关系[16]、稀疏重构权[17]或基于测地距离的全局几何结构[18]；然后，利用已知数据集之间的对应点信息[19]或样本点的几何结构[18,20,21]挖掘不同数据集样本点之间的关联性；最后，将不同的流形数据集投影到共同的低维空间中，并在低维空间中从特征层[3,18]或实例层[22]保持每个流形的局部几何结构和不同数据集之间样本点的关联性。

虽然流形对齐已在机器学习的许多领域中得到有效应用，但现有的流形对齐算法面临一个普遍的挑战。当数据集之间的对应点信息不充分时，仅仅利用流形数据的局部结构[20,21]或全局结构[18]难以准确挖掘不同数据集样本点之间的关联性。而这往往导致了不同流形数据集的样本无法在低维空间中准确对齐。因此，本文提出一种基于全局和局部特征匹配的流形对齐算法。首先，计算不同流形样本点之间的测地距离，并以此表示样本点之间的关联性；然后，构造每个流形样本点的局部结构，并基于局部结构计算样本点之间的相似性；最后，利用样本点之间局部特征的相似性对不同流形样本点之间的测地距离进行修正，从而更为准确地挖掘不同流形样本点之间的关联性。

本文其它章节安排如下：在第2节中，简单回顾了一种保持全局结构的流形对齐算法PGGMA(Preserving Global Geometry for Mainfold Alignment)，并提出了该算法的不足之处；在第3节中，提出了基于PGGMA的改进算法,即基于全局和局部特征匹配的流形对齐算法；在第4节中，通过实验验证了本文算法的有效性；最后，对本文算法进行了总结和展望。

2 保持全局结构的流形对齐算法

2.1 算法回顾

在这一节中，对PGGMA算法做简单回顾。给定两个采自流形X和Y上的数据集X={x1,…,xm}，Y={y1,…,yn}，其中X∈Rpx×m,Y∈Rpy×n,px、py分别表示数据集X和Y中样本点的维度。PGGMA为半监督流形学习算法，需要预先给定部分样本点的对应信息作为先验知识。假设X、Y中给定的对应点表示为，xai↔ybi，ai∈[1,m],bi∈[1,n],i∈[1,l],其中l是给定的对应点个数。PGGMA算法首先估计每个样本点到其余样本点的测地距离，并以此表示样本点的全局几何结构，然后将所有样本点投影到一个共同的低维空间，并在低维空间中尽可能地保持样本点的全局几何结构。算法主要包括下面三个步骤：

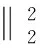
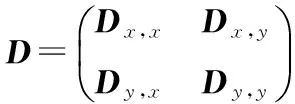
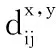
(1)

由于xi与yj的维度不同，无法直接计算两者之间的距离。在文献[18]中，利用对应点xau↔ybu,u∈[1,l]构造xi与yj间测地距离最短的通路，并以此计算xi与yj的测地距离，即:

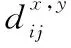
(2)

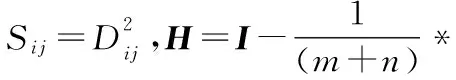
(3)

的最大d个特征值以及对应的特征向量γ=[γ1,…,γd]。记[α,β]T=[γ1,…,γd]，则可以获得线性映射α和β，以及X和Y在d维空间中的投影坐标αTX和βTY。

2.2 存在的问题

在PGGMA算法中，算法的核心在于如何有效地联结两个不同流形。PGGMA利用式(2)估计两个流形样本点之间的测地距离，用于联结两个不同的流形。但是，当给定少量对应点时，这种测地距离的估计方式可能无法准确反映不同流形样本点之间的关联性。接下来，本文以一个模拟例子来说明这个问题。

假设数据集X和Y采自于两条不同的曲线，即:

yi=[0.5sin(tj),0.5cos(tj)]T,

已知两个数据集中有三组对应点x10↔y10、x70↔y70、x130↔y130，如图1所示。基于这三组对应点并利用式(2)可以计算出所有xi与yi之间的距离。比如，x17和y20、x20和x20之间的距离为:

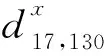
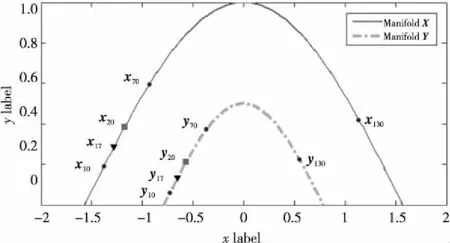
Figure 1 Manifold curves X and Y图1 流形曲线X和Y

从计算结果看，x17和y20的距离小于x20和y20之间的距离，即x17和y20更有可能是匹配点。但实际上，x20和y20是对应点。

从这个例子可以看出，当已知的对应点信息不够充分时，按照式(2)估计的测地距离难以准确联结两个流形。

3 基于全局和局部特征匹配的流形对齐算法

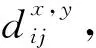
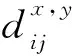
(4)

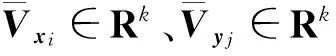
(5)

其中，φ是正则化参数，和分别表示曲线和的梯度。在本文的实验中，φ固定设置为1。从式(4)和式(5)可以看出，如果xi和yj具有相似的局部结构，则会较小，从而减小xi和yj的距离。

Figure 2 Alignment results of several manifold alignment algorithms on FacePix data set图2 几种不同流形对齐算法在FacePix数据集上的对齐结果

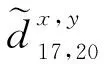
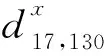
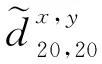
在新的距离计算公式下，x20和y20之间距离小于x17和y20，表明x20比x17更有可能是y20的匹配点。这说明综合利用样本点的全局和局部特征，能更好地联结两个不同流形。

4 数值实验

为了体现本文算法的有效性，本文在FacePix和COIL-20两个实际数据集上，同三种半监督的算法PGGMA[18]、PAMA(Procrustes Analysis for Manifold Alignment)[22]、SSMA(Semi-Supervised Manifold Alignment)[19]和一种非监督的算法UNMA(UN-supervised Manifold Alignment)[21]进行实验对比。

4.1 度量方式和参数设置

本文实验目的是对目标领域数据集X={xi|i=1,…,m}和辅助领域的数据集Y={yj|1,…,n}中的图像进行匹配。对目标领域中的图像xi，如果辅助领域数据集中的图像yj是其在低维投影空间的最近点，则yj是xi的匹配图像。记θxi和θyj为图像xi与yj中人脸或物体的旋转角度。如果|θxi-θyj|≤θ，则yj为xi的准确匹配图像。为了量化图像匹配的结果，本文提出匹配准确率和平均角度差两种度量方式：

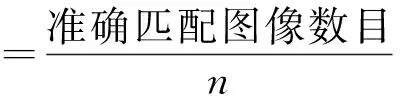
其中，n是目标领域图像的数目。

邻域参数k和目标维度d是本文算法和对比算法PGGMA、PAMA、SSMA均涉及的参数。在本文实验中，均设置k=10,d=10。

4.2 FacePix人脸图像数据集

在这个实验中，将流形对齐算法用于人脸姿态的对齐。所用到的图像数据来自于FacePix人脸图像数据，一共含有30个人不同人脸姿态下的图像。本文选取其中两组男女头像进行对比实验。每组数据集包含181个128*128规模的图像，由摄像机围绕头部从-90°旋转到+90°，每间隔1°拍摄而成。将每张图像缩小成32*32图像，再进行向量化，由此得到两个1024*181的数据集。

假设两个数据集已知对应点有6个，采用流形对齐算法将两个数据集投影到共同的10维空间。图2列出了本文算法和PGGMA、PAMA、SSMA、UNMA的匹配结果。图中用黑色加粗边框标注出错误匹配的图像，即与原图像的角度差大于10°的匹配图像。本实验中，由于无监督算法UNMA只利用样本点的局部几何结构进行匹配，实验结果并不理想。在半监督算法中，本文算法明显优于其余算法，能很好地在辅助领域中寻找到目标领域图像的匹配点。进一步地，本文设计实验对匹配结果进行量化。图3a列出了角度差从0°到10°变化时，几种算法的图像匹配准确率。显然，在不同的角度差下，本文算法的图像匹配准确率明显高于其它流形对齐算法。

Figure 5 Alignment results of several manifold alignment algorithms on the objects obj1 and obj13 from the COIL-20 database图5 几种流形对齐算法在COIL-20数据库上目标obj1和obj13的对齐结果

Figure 3 Maching accuracies on FacePix data set图3 FacePix数据集上的匹配准确率

衡量半监督流形对齐算法性能的一个重要指标是算法对先验信息的依赖性。本文设计实验以验证半监督流形对齐算法在给定不同个数对应点情况下的效果。图3b列出了几种半监督流形对齐算法在对应点个数从2到10时的图像匹配准确率(角度差θ=5)。从图3中可以看出，PGGMA、PAMA、SSMA对先验信息有较高的要求。要达到60%的匹配准确率，三种算法分别要求给定9个、6个和10个对应点作为先验信息。而本文算法在少量先验信息的情况下(l=3)，图像匹配准确率就可以超过80%。这主要是因为本文算法综合样本点的局部特征和全局特征以联结不同流形。当获取的先验信息不充分时，这比只依赖给定对应点联结流形具有更高的可靠性。

4.3 COIL-20数据库

在这个实验中,将流形对齐算法用于COIL-20数据库。此数据库由20个不同物体在不同旋转角度下的图像构成。相机围绕物体旋转360°，每次旋转5°共拍摄72幅128*128大小的图像。本实验选择7个不同的物体进行实验，物体图像见图4。将每张图像缩小为32*32规模，再转化成一个1 024维向量，这样得到7个规模为1024*72的数据集。

Figure 4 Seven experiment objects in the COIL-20 database图4 COIL-20数据库中的七个实验目标

本文首先用obj1和obj13进行可视化匹配效果实验。给定7个对应点，采用不同流形对齐算法将两个数据集投影到共同的10维空间。图5列出了本文算法和PGGMA、PAMA、SSMA、UNMA的匹配结果。图中用黑色加粗边框标注了错误匹配的图像，即与原图像角度差大于15°的匹配图像。显然，本文算法能在obj13中找到所列出的obj1匹配图像。进一步地，本文对匹配结果进行量化实验。图6a列出了几种算法在角度差θ从0°到25°的图像匹配准确率。如图6所示，本文算法的匹配准确率高于其它流形对齐算法。当θ=20°时，本文算法的匹配准确率超过90%。

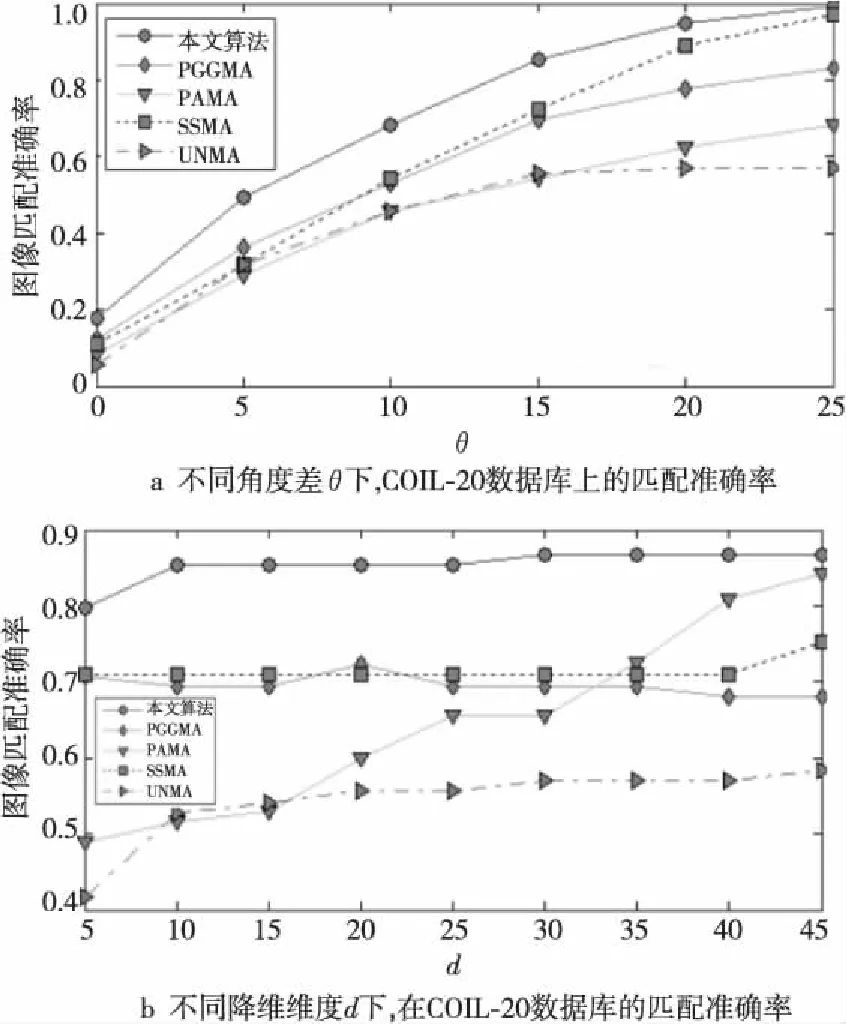
Figure 6 Maching accuracies on COIL-20 database图6 COIL-20数据库上的匹配准确率

本文算法和PGGMA、PAMA、SSMA、UNMA等算法都涉及到目标维度参数d。本文设计实验以验证不同流形对齐算法对参数d的敏感性。给定l=7个对应点并固定角度差θ=15°，图6b列出了不同流形对齐算法在d从5增大到45时的图像匹配准确率结果。显然，本文算法在不同d下的结果均明显优于其它算法。更重要的是，当d从10增大到45时，本文算法的结果变化不大。

这表明本文算法对参数并不敏感。

最后，本文将obj1对应的数据集作为目标数据集，obj2、obj3、obj4、obj7、obj9、obj13等6个物体对应的数据集作为辅助数据集进行对齐实验。给定l=5,8,11等不同个数的对应点，表1列出了本文算法和PGGMA、PAMA、SSMA、UNMA在这6个辅助数据集上的平均角度差。显然，越小的平均角度差意味着越好的对齐效果。从表1可以看出，所有算法在6个辅助数据集上的平均角度差都随着l的增大而减小。这表明对应点个数的增加能帮助流形对齐算法更好地联结不同流形。值得注意的是，当只给定很少的对应点时(l=5)，本文算法在6个辅助数据集上都能取得较小的平均角度差。这进一步说明了本文算法在少量先验信息情况下的有效性。

5 结束语

本文提出了一种新的算法，利用测地距离构造不同流形样本点之间的关联性，再利用样本点之间局部几何结构的相似性进行修正，以更为准确地挖掘不同流形样本点之间的关联性。在本文提出的半监督流形对齐算法中，需要利用给定点的信息构造两个流形样本点之间的测地距离。如何扩展到在无监督流形对齐算法下，保持全局和局部特征样本点关系，是将来本文需要研究的内容。此外，当流形采样比较稀疏或数据存在噪声时，基于局部距离度量流形样本之间的相似性可能并不准确。如何挖掘更鲁棒的局部结构以衡量流形样本点之间的相似性，也是将来的研究内容。

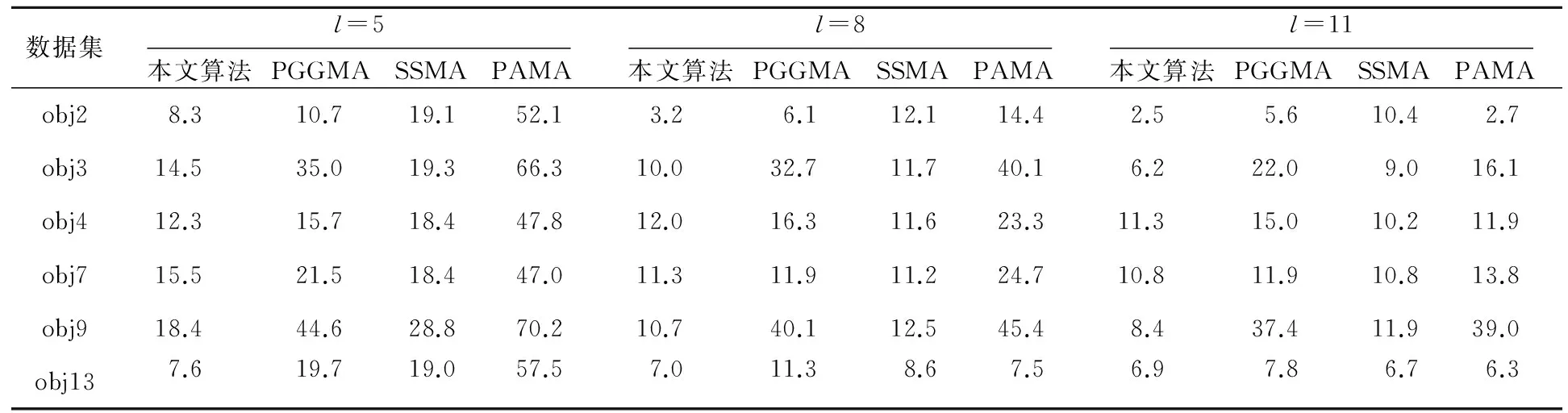
Table 1 Average errors of matching angles of several manifold alignment algorithms on six different objects from the COIL-20 database

[1] Martinez A M,Kak A C. PCA versus LDA[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2001,23(2):228-233.

[2] Seung H S,Lee D D.The manifold ways of perception[J].Science,2000,290(5500):2268-2269.

[3] Wang C,Mahadevan S.A general framework for manifold alignment[C]∥Proc of AAAI,2009:101-109.

[4] Tenenbaum J,Silva V,Langford J.A global geometric framework for nonlinear dimensionality reduction[J].Science,2000,290(5500):2319-2323.

[5] Roweis S T, SaulL K.Nonlinear dimensionality reduction by locally linear embedding[J].Science,2000,290(5500):2323-2326.

[6] Zhang Z.Principal manifolds and nonlinear dimensionality reduction via tangent space alignment[J].Scientific Computing,2005,6(1):313-333.

[7] Belkin M. Laplacian eigen maps for dimensionality reduction and data representation[J].Neural Computation,2003,15 (6):1373-1396.

[8] Blei D,Ng A,Jordan M.Latent dirichletallocation[J].Journal of Machine Learning Research,2003,3(9):993-1022.

[9] Deerwester S,Dumais S T,Furnas G W,et al.Indexing by latent semantic analysis[J].Journal of the American Society for Information Science,1990,41(6):391-407.

[10] Diaz F,Metzler D.Pseudo-aligned multilingual corpora[C]∥Proc of International Joint Conference on Artificial Intelligence,2007:2727-2732.

[11] Bradski G R,Davis J W.Motion segmentation and pose recognition with motion history gradients[J].Machine Vision and Applications,2002,13(3):174-184.

[12] Nigam K,Ghani R.Analyzing the effectiveness and applicability of cotraining[C]∥Proc of the 9th International Conference on Information and Knowledge Management,2000:86-93.

[13] Zhen C,Hong C,Shiguang S,et al.Generalized unsupervised manifold alignment[C]∥Proc of NIPS,2014:2429-2437.

[14] Dan L P,Yun Q T,Jun Z.Visualization of hyperspectral imaging data based on manifold alignment[C]∥Proc of International Conference on Pattern Recognition,2014:1051-1057.

[15] Heili A.Improving head and body pose estimation through semi-supervised manifold alignment[C]∥Proc of IEEE International Conference on Image Processing,2014:1912-1916.

[16] He X.Locality preserving projections[C]∥Proc of the 16th Advances in Neural Information Processing Systems,2003:153-160.

[17] Jian C L,Zhang Y.Manifold alignment based on sparse local structures of more corresponding pairs[C]∥Proc of the 23rd International Joint Conference on Atificial Intelligence,2013:2862-2868.

[18] Wang C,Mahadevan S.Manifold alignment preserving global geometry[C]∥Proc of the 23rd International Joint Conference on Artificial Intelligence,2013:1743-1749.

[19] Ham J,Lee D,Saul L.Semi-supervised alignment of manifolds[C]∥Proc of International Workshop on Artificial Intelligence and Statistics,2005:120-127.

[20] Yu P,Feng H C,Fu S H,et al.Unsupervised image matching based on manifold alignment[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2012,34(8):1658-1664.

[21] Wang C,Mahadevan S.Manifold alignment without correspondence[C]∥Proc of the 21st International Joint Conference on Artifical Intelligence,2009:1273-1278.

[22] Wang C,Mahadevan S.Manifold alignment using procrustes analysis[C]∥Proc of the 25th International Conference on Machine Learning,2008:1120-1127.

[23] Perth W A, Mian A,Lin L,et al.Unsupervised iterative manifold alignment via local feature histograms[C]∥Proc of IEEE Winter Conference on Applications of Computer Vision,2014:572-579.