探讨初中平面几何中的线段最值问题

2018-03-03江苏省启东市鹤城初级中学

中学数学杂志 2018年4期

关键词：对称点动点轴对称

☉江苏省启东市鹤城初级中学印卫

在初中平面几何中，有一类在动态问题中求线段最值的问题.这类题涉及的知识面广，综合性强，要求解题者具有较强的数学转化能力及创造意识.下面，我们一起来探讨一下此类问题的解法.

一、运用轴对称变换解决线段最值问题

例1（2013年内江）如图1，已知菱形ABCD的两条对角线的长分别为6和8，M、N分别是边BC、CD的中点，P是对角线BD上一点，则PM+PN的最小值=_______.

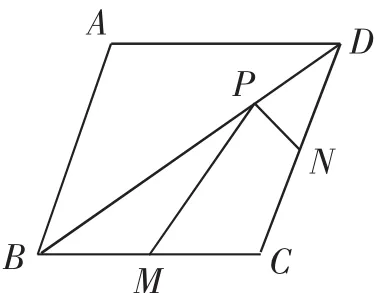
图1

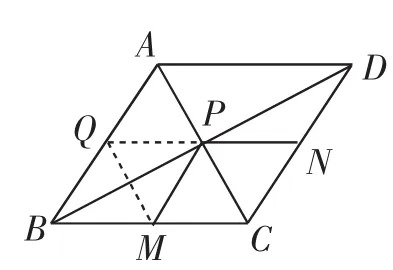
图2

分析：M和N都是定点，且都在直线BD的同侧，这个问题同人教版八年级上册第85页问题1.如图2，作M关于BD的对称点Q，连接PQ.则PM=PQ，把PM转化为PQ，于是，求PM+PN的最小值即求PQ+PN的最小值.因为Q，N为定点，根据“两点之间线段最短”可得线段QN即为所求.

例2（2017年启东市一模）如图3，已知正比例函数y=kx（k＞0）的图像与x轴相交所成的锐角为70°，定点A的坐标为（0，4），P为y轴上的一个动点，M、N为函数y=kx（k＞0）的图像上的两个动点，则AM+MP+PN的最小值为（）.

图3

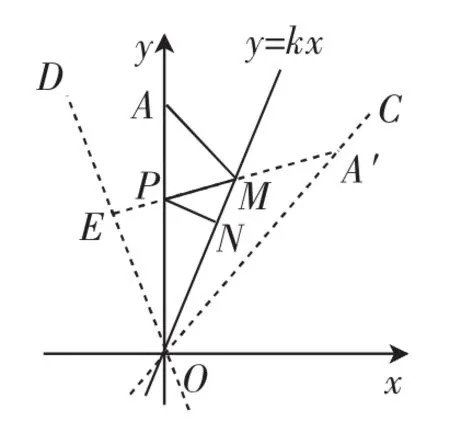
图4

A.2

B.4sin40°

C.2

D.4sin20°（1+cos20°+sin20°cos20°）

分析：如图4所示，直线OC、y轴关于直线y=kx对称，直线OD、直线y=kx关于y轴对称，A′是A关于直线y=kx的对称点，E是N关于y轴的对称点.于是求AM+MP+PN的最小值就是求A′M+PM+PE的最小值.因为A′是定点，其他都是动点，运用“垂线段最短”的原理，作A′E垂直直线OD，垂足为E.所以AM+PM+PN=A′M+PM+PE=A′E最小.在Rt△A′EO中，因为∠A′EO=90°，OA′=4，∠A′OE=

策略：此类题的背景材料往往是角、矩形、菱形、正方形等具有轴对称性的图形，解题时，通过轴对称转化其中一条或几条线段，再运用“两点之间线段最短”或“垂线段最短”的原理，实现“化折为直”就可以解决.

二、运用平移变换解决线段最值问题

例3（人教版八年级上册第86页问题2造桥选址问题）如图5，A和B两地在一条河的两岸，现要在河上造一座桥MN.桥造在何处才能使从A到B的路径AMNB最短？在图中画出路径，不写画法但要说明理由.（假定河的两岸是平行的直线，桥要与河垂直）

图6

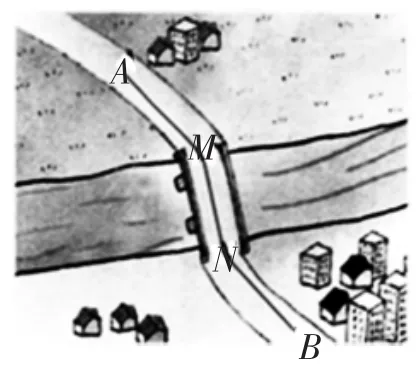
图5

分析：虽然A、B两点在河的两侧，但连接AB的线段与河岸不垂直.关键在于AM+BN最小，但AM与BN未连在一起，所以，应该进行以下操作：如图6，把BN沿与河岸垂直的方向平移至MB′，这样，相当于把BN转化为MB′.于是，求AM+BN最小，相当于求AM+MB′最小.根据“两点之间线段最短”，线段AB′最短，即AM+BN最短.故桥建立在MN处符合题意.

策略：本题通过平移变换，转化一条线段，从而顺利运用“两点之间线段最短”解决了问题.

三、运用平移及轴对称变换解决线段最值问题

例4 （2012年南宁）已知点A（3，4），B为直线x=-1上的动点，设B（-1，y）.

（1）如图7，若点C（x，0）且-1＜x＜3，BC⊥AC，求y与x之间的函数关系式.

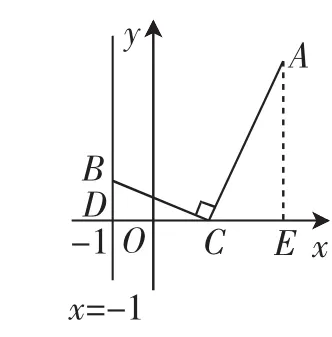
图7

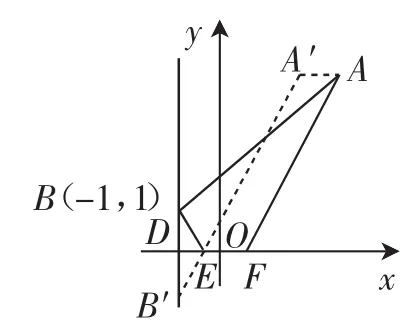
图8

（2）在（1）的条件下，y是否有最大值？若有，请求出最大值；若没有，请说明理由.

（3）如图8，当点B的坐标为（-1，1）时，在x轴上另取两点E，F，且EF=1.线段EF在x轴上平移，线段EF平移至何处时，四边形ABEF的周长最小？求出此时点E的坐标.

分析：本题中的第（3）题涉及的问题是线段的最值问题.如图8，由于线段AB与线段EF为定值，所以求四边形ABEF周长的最小值，相当于求BE+AF的最小值，于是问题就转化为当点E在x轴的什么位置时，BE+AF最小.此问题是例1与例3的综合.先把线段AF左移1个单位至A′E，求BE+AF的最小值就转化为求BE+A′E的最小值.接下来作点B关于x轴的对称点B′，连接A′B′，交x轴于点E，点E就这样确定下来后，再在x轴上截取线段EF=1，则此时四边形ABEF的周长最小.

策略：本题综合性比较强，先运用图形的平移把题目转化为例1模型，再用例1模型解决问题.

四、运用旋转解决线段最值问题

例5（2014年通州区一模）如图9，边长为2a的等边△ABC中，M是高CH所在直线上的一个动点，连接MB，将线段BM绕点B逆时针旋转60°得到BN，连接HN.则在点M运动过程中，线段HN长度的最小值是（）.

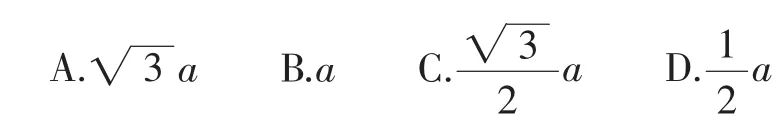
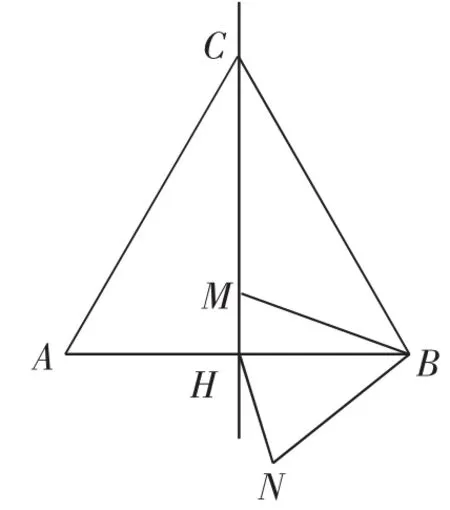
图9

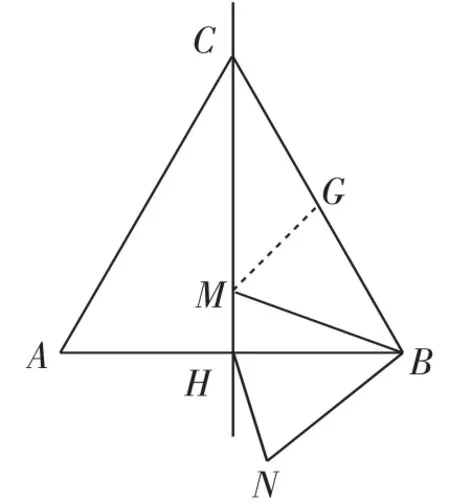
图10

分析：由于线段HN不改变位置无法解决问题，只能根据题意转化线段HN.把△HNB绕着点B顺时针旋转60°得△GMB，此时G正好落在BC的中点处.这样很顺利地就把线段HN转化为线段MG.于是根据“垂线段最短”的原理，当MG⊥CH时，MG最短，即HN最短.

策略：当题目中有明显的旋转变换而又无法直接解决线段最值问题，想到用旋转变换反过来转回，以达到转化线段的目的.

五、运用轨迹解决线段最值问题

例6 （2016年安徽）如图11，Rt△ABC中，AB⊥BC，AB=6，BC=4，P是△ABC内部的一个动点，且满足∠PAB=∠PBC，则线段CP长的最小值为（）.

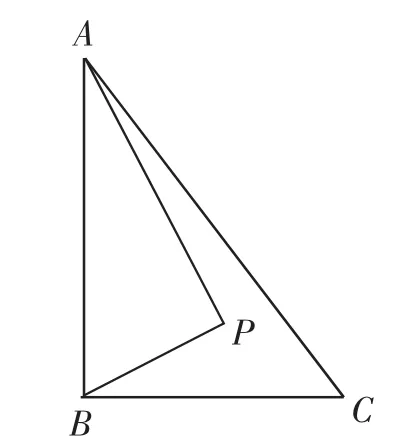
图11

图12

分析：本题显然不能用上述方法解决.由于C是定点，P是动点，所以CP的大小就由点P的位置来决定.本题就转化为当点P运动到△ABC内何处时，线段CP的长最小.于是，我们就想到点P的运动轨迹问题.由∠PAB=∠PBC，得∠APB=90°，所以点P在以AB为直径的⊙O上，连接OC交⊙O于点P，此时PC最小.

策略：本题解题关键是确定点P的位置，明确点P的运动轨迹是圆，然后利用图13所示的基本图形求出最值.

综合分析：以上方法，无论是轴对称、平移还是旋转或是轨迹圆，都是通过几何作图分析，运用基本原理、基本图形解决的.但有些几何问题，并不一定都通过几何方法来解决的，有时要通过函数或方程思想来解决.

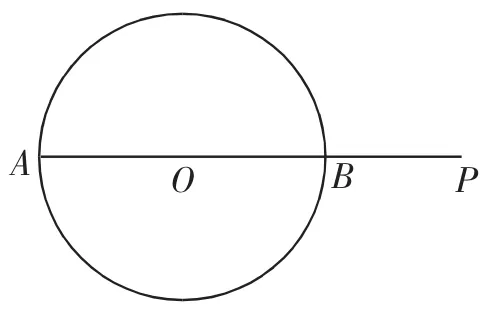
图13

六、运用函数思想解决线段最值问题

例7（2016年日照）如图14，直线与x轴、y轴分别交于点A，B，Q是以C（0，-1）为圆心、1为半径的圆上一动点，过点Q的切线交线段AB于点P，则线段PQ的最小是_______.

分析：此题中，点P的位置随着点Q的位置变化而变化，又由于点Q在圆上，且PQ与圆C相切，所以用作图的几何方法很难解决.这时，我们试一下代数思想：函数思想，想一下线段PQ与哪些线段有关.不妨运用切线常见的辅助线，连接CQ，连接CP，构造了直角△PCQ，从而所以PQ的大小随着CP的变化而变化，CP越小，PQ越小，而当CP垂直AB时CP最小.求出了CP的最小值再代入上式就可求出PQ的最小值.