重视反思 用好资源 总结提升——分类讨论思想的应用

☉江苏省兴化市戴泽初级中学 马爱平

☉江苏省兴化市教育局教研室 陈德前

数学思想方法是数学基础知识的重要组成部分，教材中没有专门的章节介绍它，而是伴随着基础知识的教学而展开的.在初中数学总复习中一定要重视对常用数学思想方法的复习，因为它们是数学的精髓，是解题的指导思想，更能使人受益终身.现以分类讨论思想为例，谈谈对初中数学总复习中进行数学思想方法专题复习的一些浅见，供研讨.

一、分类讨论思想简析

分类讨论思想是在解题的过程中，将某一数学对象根据它的本质属性，按照一定的原则或标准将它分成若干类，然后逐类进行讨论解决，再把这几类的结论汇总，得出问题的完整答案的一种思想方法.《义务教育数学课程标准》（2011年版）（以下简称《课标》）指出：“分类是一种重要的数学思想.学习数学的过程中经常会遇到分类问题，如数的分类，图形的分类，代数式的分类，函数的分类等.在研究数学问题中，常常需要通过分类讨论解决问题，分类的过程就是对事物共性的抽象过程.教学活动中，要使学生逐步体会为什么要分类，如何分类，如何确定分类的标准，在分类的过程中如何认识对象的性质，如何区别不同对象的不同性质.通过多次反复的思考和长时间的积累，使学生逐步感悟分类是一种重要的思想.学会分类，可以有助于学习新的数学知识，有助于分析和解决新的数学问题.”可见，掌握分类讨论思想的精髓，会用分类讨论的思想分析和解决新的数学问题，是《课标》中的基本要求.正因为如此，分类讨论思想已成为中考重点考查的思想方法，题型有选择题、填空题和解答题，试题难度一般都较大.

在解决数学问题时，有时会由于被研究对象的属性不同，导致问题结果的不同，因而需对不同属性的对象进行分类研究；或者由于在研究问题过程中会出现不同情况，因而需对不同情况进行分类研究.通过分类讨论，可以将复杂的问题转化为若干个简单的问题，使我们能更清楚地看清问题的本质，同时分类的范围为解题增加了条件，从而使得问题变得易于解决，起到了化繁为简，化难为易的作用.

用分类讨论思想解决问题的一般步骤是：（1）明确讨论对象，弄清讨论范围；（2）选择分类标准，进行合理分类；（3）按类寻找思路，逐类解决问题；（4）进行总结归纳，作出完整结论.

应用分类讨论思想解决问题，关键是要掌握正确分类的两个原则：（1）分类的对象是确定的，分类的标准是统一的；（2）分类应当不重复，不遗漏.分类应按同一标准进行，即每次分类不能同时使用几个不同的分类根据.

二、分类讨论专题典例解读

1.由字母取值不确定引起的分类讨论

例1（2017年内蒙古自治区呼和浩特市中考题）已知关于x的不等式

（1）当m=1时，求该不等式的解集；

（2）m取何值时，该不等式有解，并求出解集.

解读：本题是含字母系数的不等式问题，是中考中考查分类讨论思想时常设计的题型.当m＝1时为常系数一元一次不等式，其解法与解一元一次方程类似，但在去分母和化系数为1时，要注意不等号的方向是否改变；当m为任意实数时，要求使该不等式有解时m的值（或范围），并求出解集，属解含字母系数的不等式问题，由于m+1的取值情况未知，所以要分类讨论求解.先确定不等式有解的条件，再在有解的条件下，分类求出解集.必须注意：（1）当m=-1时，不等式为0x＜0，它对一切实数x均不成立，故此时不等式无解；（2）将不等式化为（m+1）x＜2（m+1）后，不能直接两边同除以（m+1）得到x＜2.

解：（1）当m=1时，不等式为，去分母得2-x＞x-2，解得x＜2.

（2）去分母得2m-mx＞x-2，移项合并得（m+1）x＜2（m+1）.当m≠-1时，不等式有解.当m＞-1时，不等式解集为x＜2；当x＜-1时，不等式的解集为x＞2.

2.由绝对值的定义引起的分类讨论

例2（2015年江苏省泰州市中考压轴题改编）如图1，已知一次函数y=2x-4的图像与x轴、y轴分别相交于点A、B，点P在该函数的图像上，点P到x轴、y轴的距离分别为d1、d2.当d1+d2=3时，求点P的坐标.

图1

解读：这是一道一次函数综合题，解法较多，能考查众多的数学核心知识.由于点P在一次函数y=2x-4的图像上，因此可以设P（x，2x-4），由P到x轴、y轴的距离分别为d1、d2，根据绝对值的几何意义，可将距离d1和d2分别转化为含字母x的绝对值，得d1+d2=|x|+|2x-4|，再利用d1+d2=3即可得到含绝对值符号的方程|x|+|2x-4|=3，然后根据绝对值性质，按x的不同范围进行分类讨论求解.本题中出现了两个绝对值符号，分段去掉绝对值符号是关键.可采用“零点分区间法”来思考：由x＝0和2x-4＝0，得x＝0和x＝2，则分为x＜0，0≤x≤2，x＞2这三段来分类求出x的值，即可确定出点P的坐标，但要注意检验取舍.

解：设P（x，2x-4），所以d1+d2=|x|+|2x-4|.因为d1+d2=3，所以|x|+|2x-4|=3.当x＞2时，有x+2x-4=3，解得x=，此时当0≤x≤2时，有x+4-2x=3，解得x=1，此时P（21，2）；当x＜0时，有-x+4-2x=3，解得x=与x＜0矛盾，应舍去.综上所述，点P的坐标为（1，2）或

3.由对应关系不确定引起的分类讨论

例3（2017年江苏省南通市中考题）我们知道，三角形的内心是三条角平分线的交点，过三角形内心的一条直线与两边相交，两交点之间的线段把这个三角形分成两个图形，若有一个图形与原三角形相似，则把这条线段叫这个三角形的“内似线”.

（1）等边三角形的“内似线”的条数为__________；

（2）如图2，在△ABC中，AB=AC，点D在AC上，且BD=BC=AD.求证：BD是△ABC的“内似线”；

图2

图3

（3）如图3，在Rt△ABC中，∠C=90°，AC=4，BC=3，E，F分别在边AC，BC上，且EF是△ABC的“内似线”，求EF的长.

解读：这是一道阅读理解题，理解三角形的“内似线”的概念是解题的关键.（1）过等边三角形的内心分别作三边的平行线，利用平行线说明相似三角形即可得出答案；（2）由等腰三角形的性质得出∠ABC=∠C=∠BDC，证△BCD∽△ABC即可；（3） 由于∠C=90°，则△CEF与△CAB相似，分两种情况：①△CEF∽△CAB；②△CFE∽△CAB.因此，需分两种情况求出EF的长.

解：（1）等边三角形“内似线”的条数为3.理由：过等边三角形的内心分别作三边的平行线，如图4所示，则△AMN∽△ABC，△CEF∽△CBA，△BGH∽△BAC，所以MN、EF、GH是等边三角形ABC的“内似线”.

图4

（2）因为AB=AC，BD=BC=AD，所以∠ABC=∠C=∠BDC，∠A=∠ABD，所以∠A=∠ABD=∠DBC=36°，所以BD平分∠ABC，即BD过△ABC的内心.因为∠C=∠C，∠DBC=∠A，所以△BCD∽△ABC，所以BD是△ABC的“内似线”.

（3）如图5，设I为△ABC的内心，过点I分别作三边的垂线，垂足分别为P，M，N，则IP=IM=IN.在Rt△ABC中，由勾股定理得AB=5，由三角形面积公式得3+4+5）·IP=所以IP=IM=IN=1.①当△CEF∽△CAB时，如图5，∠CEF=∠CAB，∠EMI=∠ACB=90°，所以△MEI∽△CAB，所以所以同理可得所以②当△CFE∽△CAB时，如图6，同上可得△MEI∽△CBA，△NFI∽△CAB，所以综上可知

图5

图6

4.由图形位置不确定引起的分类讨论

例4（2015年江苏省南京市中考题）如图7，在边长为4的正方形ABCD中，请画出以A为一个顶点，另外两个顶点在正方形ABCD的边上，且含边长为3的所有大小不同的等腰三角形.（要求：只要画出示意图，并在所画等腰三角形长为3的边上标注数字3）

解读：这是一道与等腰三角形和正方形相关的画图问题，解题的关键是合理分类，而分类的标准较多，主要有：可按三角形除顶点A以外的两个顶点所在的四边形ABCD边上的情况进行分类，也可按腰和底的长分别是3来探究.具体解题时，常常将这两种分类结合在一起，构成二级分类.在确定答案时，要注意排除大小相同的等腰三角形.

图7

解：（1）等腰三角形的另两个顶点分别在AB和AD上，有两种情况：一是腰为3，如图8①，其确定方法是：以A为圆心，3为半径作弧，分别交AD、AB上的两点，连接即可；二是底为3，如图8②，其确定方法是：连接AC，以A为端点，在AC上截取1.5个单位，得到一个点，再过这个点作AC的垂线，交AD、AB上的两点，连接即可.

（2）等腰三角形的一个顶点在AB上，有两种情况：一是第三个顶点在BC上，如图8③，其确定方法是：以A为端点在AB上截取3个单位，以截取的点为圆心，以3个单位为半径画弧，交BC于一点，连接即可；二是第三个顶点在CD上，如图8④，其确定方法是：以A为端点在AB上截取3个单位，再作这条线段的垂直平分线交CD于一点，连接即可.

（3）等腰三角形的另两个顶点分别在BC和CD上，如图8⑤，其确定方法是：连接AC，在AC上，以C为端点，截取1.5个单位，过这个点作AC的垂线，交BC、DC上的两点，然后连接A与这两个点即可.

（2）对自身专业英语学习参与度的认知。有40人（2.1%）认为自身专业英语水平很好，132人（7.0%）认为自身专业英语水平好，988人（52.1%）认为自身专业英语水平一般，547人（28.8%）认为自身专业英语水平差，190人（10.0%）认为自身专业英语水平很差。自我评价程度随着年级越高而递增，且年级间差异有显著性（P=0.003），不同性别学生间差异有显著性（P=2.096×10-4），学生干部的自我评价明显高于非学生干部学生（P=1.482×10-4）。此外，专业英语题1正确率32.6%，专业英语题2正确率14.9%，反映了学生的自我评价具有一定客观性。

另解：也可以先按照腰和底的长分别是3来分类，再按照腰或底在正方形边上的情况分类：

（1）3为腰，有三种情况：一是两腰在正方形边上，如图8①；二是一腰在正方形边上，如图8③；三是腰不在正方形边上，这种情况不存在.

（2）3为底，有两种情况，一是底在正方形边上，如图8④；二是底不在正方形边上，如图8②和8⑤.

图8

5.由操作过程的不确定引起的分类讨论

例5（2015年浙江省义乌、绍兴市中考题）实验室里，水平桌面上有甲、乙、丙三个圆柱形容器（容器足够高），底面半径之比为1∶2∶1，用两个相同的管子在容器的5cm高度处连通（即管子底端离容器底5cm），现三个容器中，只有甲中有水，水位高1cm，如图9所示.若每分钟同时向乙和丙注入相同量的水，开始注水1分钟，乙的水位上升cm，则开始注水______分钟后，甲与乙的水位高度之差是0.5cm.

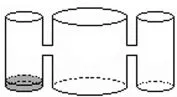
图9

解读：这是一道实验操作类的填空压轴题，由甲、乙、丙三个圆柱形容器（容器足够高），底面半径之比为1∶2∶1，注水1分钟，乙的水位上升cm，得到注水1分钟，丙的水位上升cm.设开始注水t分钟后，甲与乙的水位高度之差是0.5cm，而甲与乙的水位高度之差是0.5cm有三种情况：①当乙的水位低于甲的水位时；②当甲的水位低于乙的水位，且甲的水位不变时；③当甲的水位低于乙的水位，乙的水流向甲管，甲的水位开始上升时.因此，应分三种情况分别列方程求解.

解：因为甲、乙、丙三个圆柱形容器（容器足够高）的底面半径之比为1∶2∶1，注水1分钟，乙的水位上升cm，所以注水1分钟，丙的水位上升cm.设开始注水t分钟后，甲与乙的水位高度之差是0.5cm，甲与乙的水位高度之差是0.5cm有三种情况：①当乙的水位低于甲的水位时，有1-t=0.5，解得t=分钟）.②当甲的水位低于乙的水位，且甲的水位不变时，因为t-1=0.5，解得t=因为=6＞5，所以此时丙容器已向乙容器溢水.因为5÷（分钟），即经过分钟丙容器的水到达管子底部，乙的水位上升故1=0.5，解得.③当甲的水位低于乙的水位，且乙的水流向甲管，甲的水位开始上升时，因为乙的水位到达管子底部的时间为分钟），所以5-解得综上所述，开始注水分钟或分钟或分钟后，甲与乙的水位高度之差是0.5cm.

6.由动态问题引起的分类讨论

例6（2017年新疆乌鲁木齐市中考题）如图10，抛物线y=ax2+bx+c（a≠0） 与直线y=x+1相交于A（-1，0），B（4，m）两点，且抛物线经过点C（5，0）.

（1）求抛物线的解析式.

（2）P是抛物线上的一个动点（不与点A、点B重合），过点P作直线PD⊥x轴于点D，交直线AB于点E.

①当PE=2ED时，求P点坐标；

②是否存在点P使△BEC为等腰三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由.

解读：这是一道动态型综合压轴题，解题的关键是综合应用数学知识，灵活运用分类讨论、转化、方程、数形结合等思想方法，动静结合地进行探究.（1）由直线解析式可求得B点坐标，由A、B、C三点的坐标，利用待定系数法可求得抛物线解析式.（2）①设出P点坐标，则可表示出E、D的坐标，从而可表示出PE和ED的长，设P（x，-x2+4x+5），则可表示出E、D的坐标E（x，x+1），D（x，0）.由于P是抛物线上的一个动点，所以点P的位置分三种情况：一是P点在抛物线上AB之间；二是P点在抛物线上A点的左侧；三是P点在抛物线上B点的右侧，用字母x表示PE和ED，再利用PE=2ED构造出关于x的方程，即可求出点P的坐标.②由E、B、C三点坐标可表示出BE、CE和BC的长，由等腰三角形的性质构造出关于x的方程，可求得E点坐标和P点坐标.

解：（1）因为点B（4，m）在直线y=x+1上，所以m=4+1=5，所以B（4，5）.把A、B、C三点坐标代入抛物线解析式可得解得所以抛物线解析式为y=-x2+4x+5.

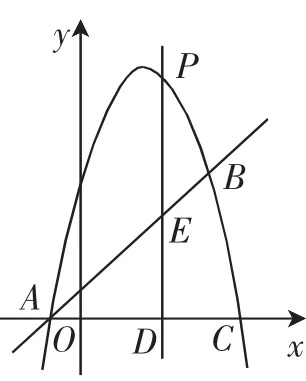
图10

（2）①设P（x，-x2+4x+5），则E（x，x+1），D（x，0）.

ⅰ当P点在抛物线上AB之间时，PE=-x2+4x+5-x-1=-x2+3x+4，DE=x+1.因为PE=2ED，即-x2+3x+4=2（x+1），解得x1=2，x2=-1，所以点E（2，3）或E（-1，0），E（-1，0）与点A重合舍去，此时P（2，9）.

ⅱ当P点在抛物线上点A左侧时，PE=x+1+x2-4x-5=x2-3x-4，ED=-x-1.因为PE=2ED，即x2-3x-4=2（-x-1），解同上.

ⅲ当P点在抛物线上点B右侧时，PE=x+1+x2-4x-5=x2-3x-4，ED=x+1.因为PE=2ED，即x2-3x-4=2（x+1），解得x1=6，x2=-1，所以点E（6，7）或E（-1，0），E（-1，0）与点A重合舍去，此时P（6，-7）.

综上可知P点坐标为（2，9）或（6，-7）.

②设P（x，-x2+4x+5），则E（x，x+1），B（4，5），C（5，0），所 以当△BEC是等腰三角形时，分三种情况：

综上所述，存在点P使△BEC为等腰三角形，坐标为

三、分类讨论专题复习建议

1.重视反思，总结方法

在教学中，要重视帮助学生进行解题后的反思，总结出常见问题的分类方法：（1）对于解含字母系数的不等式问题，先要按照不等式有解和无解的条件来分类，在有解的前提下求解时，再按照未知数系数的正负性来分类的；（2）对于含有绝对值的问题，一般都需去掉绝对值符号，这就要根据绝对值性质进行分类讨论，可采用“零点分区间法”来确定分类的标准；（3）对于全等三角形、相似三角形问题，可以按照顶点的不同对应顺序来分类；（4）对于等腰三角形问题，既可以按照顶角与底角来分类，也可以按照腰和底来分类；（5）对于实验操作类问题，可以按照操作中出现的不同情况进行分类；（6）对于动态问题，要根据图形可能出现的不同位置来分类.恰当地分类，可以避免以偏概全，丢值偏解.

2.暴露过程，用好资源

学生在解决分类讨论问题时常犯的错误主要有：（1）分类不正确，不能不重复又不遗漏地进行分类（如例4中的分类出现混乱）；（2）忽视对分类后得到的解的检验 （如例2中没有把舍去 ），结果造成多解或漏解；（3）对分类后得到的相同结果持怀疑态度（如例3中分类后求出的EF的值相同）；（4）忘记将结论汇总，致使最后的答案表述不清楚.针对这些问题，教学时可先让学生在自己审题的基础上，独立思考，写出自己的思考过程，然后合作交流，通过小组汇报、答案展示、学生讲题等形式来充分暴露学生的思维过程，教师在帮助学生总结归纳不同类型问题的特点、分类的基本策略和注意点的基础上，抓住学生（特别是中下等生）的思维盲区，引导学生对典型错误加以剖析，用好课堂生成性资源，努力做到变错为宝.

3.精讲点拨，总结提升

例4、例5、例6是三道难度很大的问题，在教学时可抓住这三个典型例题，通过师生共同剖析（主要是学生讲，教师点拨），由学生独立完成例题的求解，再分组交流体验和收获，然后全班共同总结，从思想方法的高度加以提升.例4在学生审题的基础上，让学生思考、讨论有哪些分类的方法，然后师生一起归纳出不同的分类方法，再让学生有条不紊地画出所有满足要求的图形，最后引导学生对得到的图形进行甄别，剔除形式不同而实质相同的图形；例5中由于有三个连通器，情况比较复杂，可在学生认真审题的基础上，让学生思考、讨论，弄清甲与乙的水位高度之差是0.5cm有三种情况，进而得出分类的方法，再让学生去求解；例6在学生思考、讨论的基础上，要重点对第（2）（3）两题进行精讲点拨，让学生弄清如何对点P的位置和△BEC是等腰三角形进行分类，对等腰三角形的三种情况画出分类后每一类中的静态图形，也可以通过几何画板进行演示，让学生体会分类的合理性，并用多媒体展示完整的解答，以规范学生的表达过程.在课堂小结中，要引导学生对常用的分类求解策略和数学思想方法进行提炼，使之形成基本活动经验，用以指导今后的解题活动.H