边界能量图研究的综述
2018-03-01李学良
邓 波,李学良
(1.南开大学 组合数学中心,天津 300071;2.青海师范大学 数学与统计学院,青海 西宁 810001)
图G的能量ε(G)定义为其邻接矩阵特征根的绝对值之和.设G是一个具有n个顶点的图,如果G的能量值等于n个顶点的完全图的能量值2(n-1), 则称图G为边界能量图.介绍了近年来关于边界能量图研究方面的主要结果.
图的特征根;图能量; 边界能量图;拉普拉斯能量
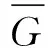
关于图能量及其应用的相关内容,可以参考文[2-5].
关于图能量,一个很自然的问题是: 哪类图具有最大的图能量? 起初,人们通常会认为当图越稠密,则对应图的图能量越大,因此认为完全图Kn具有最大的图能量,其能量值为ε(Kn)=2(n-1).实际上,存在大量的图满足其图能量是大于这个值,这类图被称为是超能量的.超能量图的概念提出后,陆续出现许多寻找和刻画超能量图的结果[6-8],不过这个研究方向很快被发现是平凡的,原因是Nikiforov通过使用概率方法证明了几乎所有的图都是超能量的.类似地,如果具有n个顶点的图G的图能量小于n(或者n-1),则图G是次能量的(或者是强次能量的),相关的研究结果见文[9-11].
次能量图的概念源于化学实验,人们在化学研究中很早就发现绝大多数分子图的能量是大于其顶点数的.1973年理论化学家England和Ruedenberg发表在J.Am.Chem.Soc.上的一篇文章曾提到这样一个问题[12]: 为什么化合物的能量总大于其化学图的阶数? 围绕这个问题,Gutman等[9]进行了相关的研究,给出具有n个顶点和最大度为Δ的树是次能量的充分条件,并且分别证明当Δ=3,4和Δ≥5时,次能量树的存在性.
定理1[9](a) 如果Δ=3, 则仅当n=4和n=7时,存在次能量树.
(b) 如果Δ=4, 则当n≥5和满足n≡k(mod 4),k=0,1,3时,存在次能量树.
(c) 如果Δ≥5, 则当n≥Δ+1时,存在次能量树.
然而当最大度Δ至多为3时,除了如下几个特殊树外,都不存在次能量树.
定理2[9]除了树S1,S2,S3和W(见图1),不存在最大度至多3的次能量树.

图1 树S1,S2,S3和W
Li等[10]证明了完全二部图K2,3是唯一含圈的满足Δ≤3的次能量连通图,同时找出了所有的满足Δ≤3的次能量连通图.
定理3[10]完全二部图K2,3是唯一含圈的满足Δ≤3的次能量连通图.
定理4[10]图S1,S2,S3,W和K2,3是仅有的5个满足Δ≤3的次能量连通图.
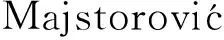
定理5[13-14]在n个顶点和Δ≤3的连通图中,恰好存在4个连通图G∈{K2,K2,2,Q,K3,3}(见图2),满足ε(G)=n.

图2 图K2,K2,2,Q和K3,3
化学图一般是指最大度不超过3的图.由上可见,只有少数几个图同时满足Δ≤3和ε(G)=n, 所以,这从理论上证明了化学家们在文[12]中观察的结果是正确的.然而当ε(G)=2(n-1)时,Gong等[15]发现存在大量的图满足这个条件.2015年,Gong等[15]提出边界能量图的概念: 如果G是一个具有n个顶点的图,满足G的图能量值与n个顶点的完全图的图能量值相等且为ε(G)=2(n-1),则称图G为边界能量的.类似地,Tura[16]把边界能量的概念推广到拉普拉斯能量.设μ1≥μ2≥…≥μn-1≥μn是图G的拉普拉斯特征根,图G的拉普拉斯能量定义如下
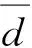
论文主要介绍近年来关于边界能量图的主要结果.内容安排如下: 第一部分介绍边界能量图的搜索与构造方面的结果; 第二部分介绍边界能量图的边数的下界; 第三部分介绍在度条件下边界能量图的结构性质方面的结果;第四部分介绍拉普拉斯边界能量图方面的结果.
1 边界能量图的搜索与构造
为了研究边界能量图的存在性,Gong等[15]通过计算机搜索的方式,找出顶点数不超过9的所有非完全边界能量图.特别地,当顶点数小于7时,不存在非完全边界能量图.当顶点数分别为7,8,9时,则有命题1~3.
命题1[15]最小的非完全边界能量图G0具有7个顶点,17条边,而且是唯一的(见图3).
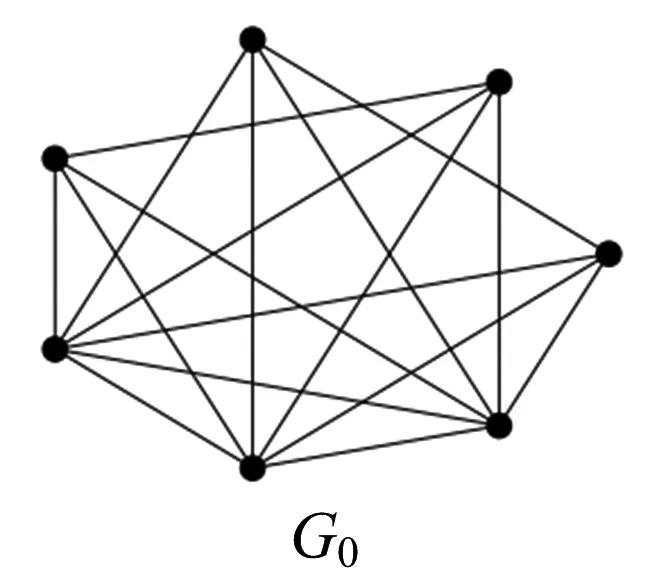
图3 最小的非完全边界能量图G0,其邻接谱为Sp(G0)={5,1,-1,-1,-1,-1,-2}
命题2[15]顶点数为8的非完全边界能量图恰好存在6个(见图4).
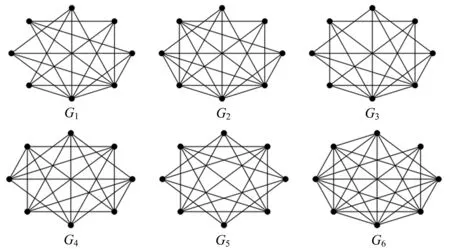
图4 6个具有8个顶点的非完全边界能量图
命题3[15]顶点数为9的非完全边界能量图恰好存在17个(见图5).
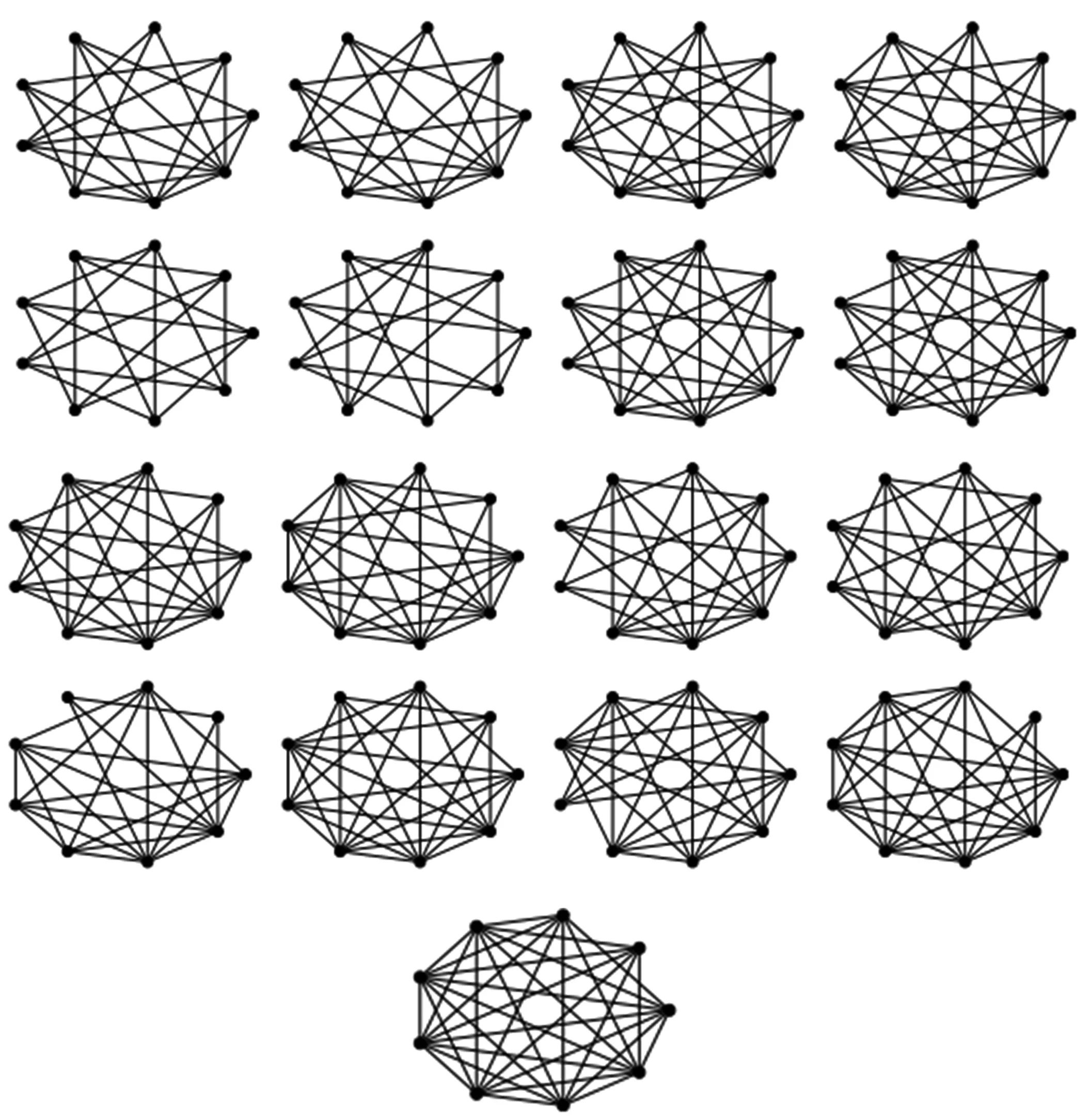
图5 17个具有9个顶点的非完全边界能量图
当顶点数为10时,Li等[20]通过计算机搜索找到49个非完全边界能量图.当顶点数为11时,Shao等[21]以同样的方式搜索找到158个非完全边界能量图.故当顶点数不超过11时,所有非完全边界能量图已全部找到.然而当顶点数很大时,也存在非完全边界能量图,而且存在大量的这样的图.接下来将通过如下几种方式展示如何构造非完全边界能量图.
方式1 图的张量积.两个图G1和G2的张量积G1⊗G2, 是以V(G1)×V(G2)为点集,两个顶点(u1,u2)与(v1,v2)相邻,当且仅当u1v1∈E(G1)和u2v2∈E(G2). 基于张量积,则有定理6.
定理6[15]设G是一个边界能量图,假设G是两个整谱图G1和G2的张量积,则|V(G1)|和|V(G2)|都是奇数.
方式2 强正则图.设G是具有n个顶点的k-正则非完全图,如果满足每对相邻顶点有a个共同的邻点,每对不相邻的顶点有c个共同的邻点,则称G是一个具有参数(n,k,a,c)的强正则图.在(n,k,a,c)-强正则图G中,如果其邻接谱满足
定理7[15]设G是一个会议图,而且满足是整谱的和非完全边界能量的,则G具有参数(9,4,1,2).
方式3 正则图、补图与图的并运算.使用正则图及其补图在图谱上的性质,Gong等[15]构造出一类边界能量图.
由定理7、8证明了边界能量图的存在性.
定理9[15]对任意的整数n≥7, 总存在顶点为n的连通非完全边界能量图.
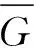
由定理11,可以推出当顶点数n满足某些整除条件,则总存在一些连通的正则的非完全边界能量图.
定理12[22]对任意满足5|(n-12)的整数n(n>12),则总存在连通的(n-5)-正则的非完全边界能量图.
定理13[22]对任意满足7|(n-16)的整数n(n>16),则总存在连通的(n-7)-正则的非完全边界能量图.
除了上述方式可以构造大量的连通非完全边界能量图外,还可以利用线图性质和一些特殊图类的图谱性质.因为已发现正则图与其对应的线图在特征根上存在一定的关系,故使用它们之间的关系可以找到非完全边界能量图.Gong等[15]发现Petersen图的线图是连通的非完全边界能量图.Hou等[23]利用门槛图的图谱性质构造出若干类非正则非整谱的连通的非完全边界能量图.
2 边界能量图边数的下界
观察图3~5可见,边界能量图都比较稠密,人们自然会考虑这样的问题: 对于任意一个连通的非完全边界能量图,至少需要多少条边? 接下来的结果会给出边界能量图的边数渐进紧的下界.先介绍顶点的r-度概念.对于整数r≥0和顶点vi∈V(G), 顶点vi的r-度定义为从vi出发的长为r的路径个数,记为dr(vi). 显然,当r=1,d1(vi)就是顶点vi的度,记为di. 当r=2,3, 分别记d2(vi)和d3(vi)为ti,σi.
定理14[22]设G是边界能量图,则

(1)
如果G是(n-3)-正则,则(1)中的界是渐进紧的.
由定理14,可以得到推论1~3.
推论1[22]设G是边界能量图,则

(2)
如果G是(n-3)-正则,则(2)中的界是渐进紧的.
推论2[22]设G是边界能量图,则

(3)
如果G是(n-3)-正则,则(3)中的界是渐进紧的.
推论3[22]设G是边界能量图,则

(4)
如果G是(n-3)-正则,则(4)中的界是渐进紧的.
3 最大(最小)度条件下的边界能量图
在化学图论中,经常研究最大度不超过4的图.因为这类图有专门的化学应用背景,在研究次能量图和其他化学指标时经常对此类图进行研究[9-10,14].对边界能量图也存在相关结果,Li等[24]对满足最大度不超过4的边界能量图的结构性质进行了刻画.
定理15[24]不存在最大度为2或3的非完全边界能量图.
定理16[24](1) 设G是具有n个顶点和最大度Δ=4的非完全边界能量图,则
(i) |E(G)|=2n或者2n-1;
(ii) |V(G)|≤21;
(iii)G是非偶图;
(iv) 特征根为0的个数为0.
(2) 设G是具有n个顶点的4正则非完全边界能量图,H是G的极大的偶子图,则|E(G)|-|E(H)|≥3.
到目前为止,在有限顶点数内,只找到3个最大度为4的边界能量图,并且都是4-正则图,其中2个具有9个顶点,另外一个具有15个顶点.另一方面,从最小度角度考虑,对边界能量图存在以下相关结果,即定理17.
定理17[24]设图G的顶点数为n,则
(1) 不存在最小度为n-2的边界能量图;
(2) 对任意整数n≥7, 总存在一个具有n个顶点,最小度为n-3的连通非完全边界能量图;
(3) 对任意偶数n≥8, 总存在一个具有n个顶点,最小度为n-4的连通非完全边界能量图.
4 拉普拉斯边界能量图
4.1 拉普拉斯边界能量图的构造与搜索
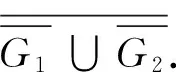
从一个孤立点开始,然后每一步或者增加一个孤立点,或者与前面的顶点都相邻,通过这种迭代方式得到的图,称为门槛图.
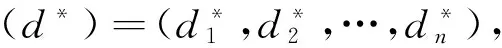
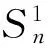
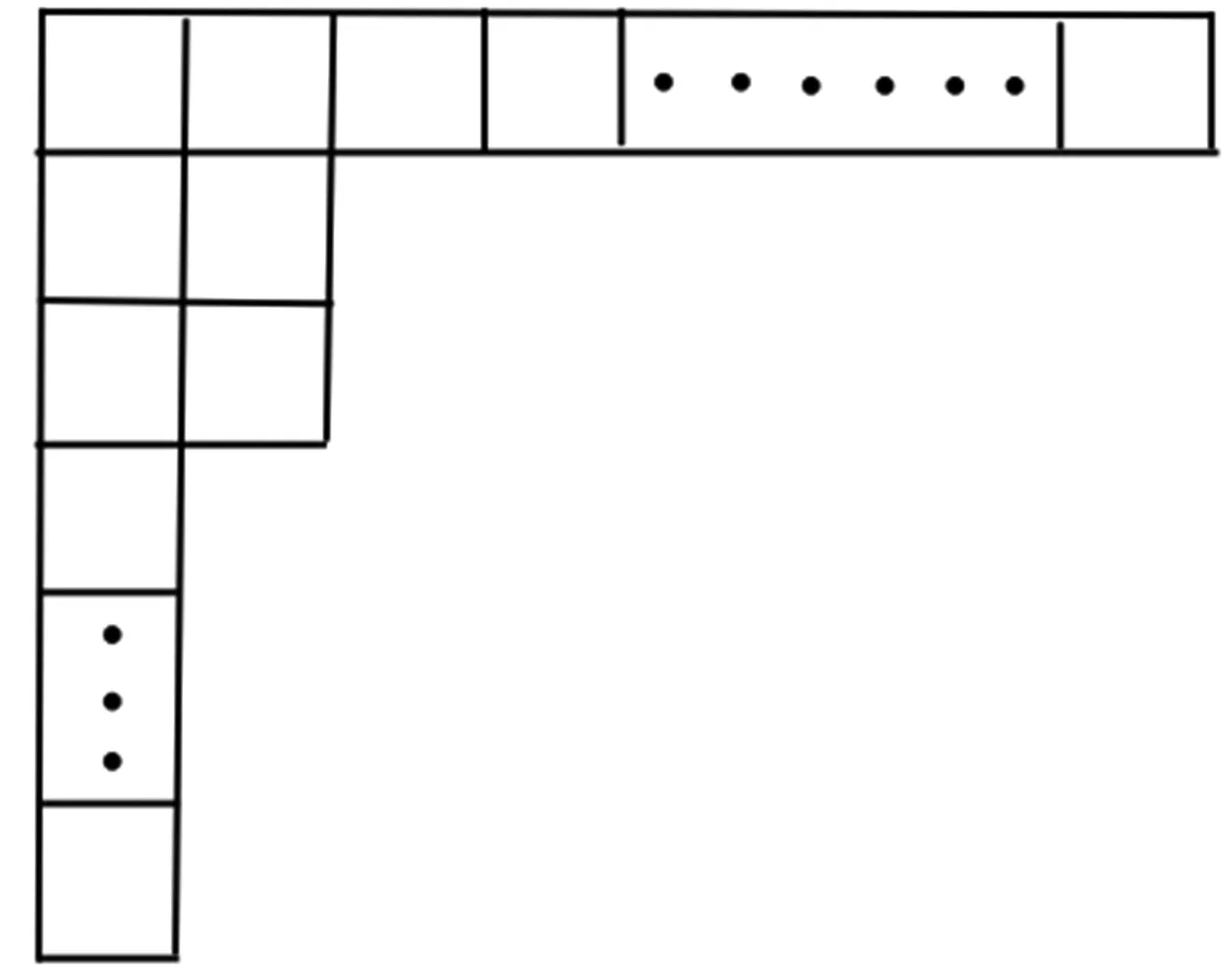
图的 Ferrers-Sylvester图
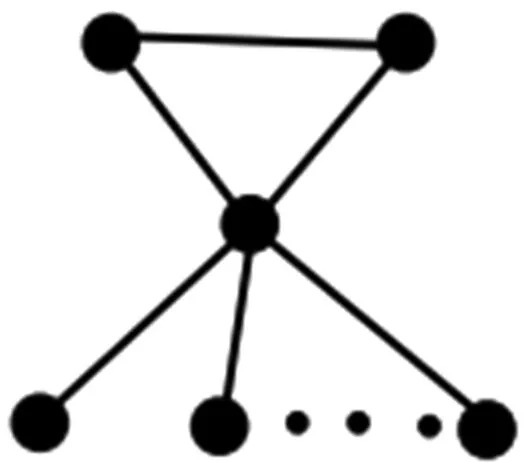
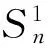
图7 门槛图
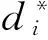
(5)
等号成立当且仅当图G是门槛图.
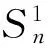
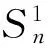
(6)
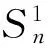
由(6),则
因此,由定理18可知,无论顶点数n是偶数或是奇数总存在拉普拉斯边界能量图,故如下的结果比Tura的结果更具有一般性.
定理19[17]对任意整数n≥4, 总存在拉普拉斯边界能量图.
当图的顶点数n在范围4≤n≤9时,所有的非完全拉普拉斯边界能量图已被找到[17],具体个数见表1.

表1 顶点数n在范围4≤n≤9的非完全拉普拉斯边界能量图个数
类似于定理6,使用图的张量积可以构造拉普拉斯边界能量图.
定理20[17]设G是拉普拉斯整谱图G1和G2的张量积,其中G1和G2分别是r1-正则和r2-正则.如果G是拉普拉斯边界能量图,则|V(G1)|和|V(G2)|都是奇数.
此外,还可以通过在完全图中去匹配的方式构造拉普拉斯边界能量图.

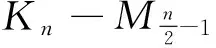
4.2 拉普拉斯边界能量图的边数和顶点数
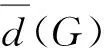
定理22[18]如果G是具有n个顶点和m条边的拉普拉斯边界能量图,则
(7)
当G是4-正则时,(7)中的界是渐进紧的.
接下来使用拉普拉斯能量的Koolen-Moulton型不等式可以得到定理23.
定理23[19]如果G是具有n个顶点和m条边的拉普拉斯边界能量图,满足最大度Δ=4, 则
(8)
当G是4-正则时,(8)中的界是渐进紧的.
类似地,由拉普拉斯能量的McClelland型不等式可以得到定理24.
定理24[19]如果G是具有n个顶点和m条边的拉普拉斯边界能量图,满足最大度Δ=4, 则
(9)
当G是4-正则时,(9)中的界是渐进紧的.
定理25[18]如果G是具有n个顶点和m条边的拉普拉斯边界能量图,则
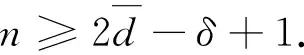
(10)
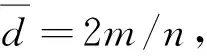
定理26[18]如果G是具有n个顶点和m条边的拉普拉斯边界能量图,满足最小度δ=1, 则
(11)
实际上,可以找到拉普拉斯边界能量图使得(11)中的等号成立.当n=4,6,8时,如下的3个图满足等号要求(见图8).
4.3 非拉普拉斯边界能量图
Deng等[18]陆续证明了所有的树、圈、完全二部图和大部分2-连通图都不是拉普拉斯边界能量图.如下这类2-连通图不是拉普拉斯边界能量图,令t(G)为图G中度为3的顶点的个数,有定理27.
定理27[18]如果G是满足最大度Δ=3和t(G)≥7的2-连通图,则G不是拉普拉斯边界能量图.
通过使用Cauchy-Schwarz不等式,定理27中的条件t(G)≥7是可以去掉的,得定理28.
定理28[19]如果G是满足最大度Δ=3的2-连通图,则G不是拉普拉斯边界能量图.
图8 顶点数分别为4,6,8和满足δ=1的拉普拉斯边界能量图
5 后续研究
观察边界能量图和拉普拉斯边界能量图已有的结果,可以看到,这些图的比较深入的结构特性并没有完全被刻画,后续研究可以考虑刻画这些图类的最大(最小)谱半径、围长、最大匹配数、最大团的点数等方面性质.
[1] GUTMAN I. Acylclic systems with extremal Hückel π-electron energy[J]. Theor Chim Acta, 1977 (45): 79-87.
[2] GUTMAN I. The energy of a graph[J]. Math-Statist Sekt Forschungsz Graz, 1978 (103): 1-22.
[3] GUTMAN I, LI X, ZHANG J. Graph energy[M]. Weinheim: Emmert-Streib, 2009: 145-174.
[4] GUTMAN I, POLANSKY O E. Mathematical concepts in organic chemistry[M]. Berlin: Springer, 1986.
[5] LI X, SHI Y, GUTMAN I. Graph Energy[M]. New York: Springer, 2012.
[6] AKBARI S, MOAZAMI F, ZARE S. Kneser graphs and their complements are hyperenergetic[J]. MATCH Commun Math Comput Chem, 2009 (61): 361-368.
[7] HOU Y, GUTMAN I. Hyperenergetic line graphs[J]. MATCH Commun Math Comput Chem, 2001 (43): 29-39.
[8] STEVANOVIC D, STANKOVIC I. Remarks on hyperenergetic circulant graphs[J]. Lin Algebra Appl, 2005 (400): 345-348.
[9] GUTMAN I, LI X, SHI Y, et al. Hypoenergetic trees[J]. MATCH Commun Math Comput Chem, 2009 (60): 415-426.
[10] LI X, MA H. All hypoenergetic graphs with maximum degree at most 3[J]. Linear Algebra Appl, 2009 (431): 2127-2133.
[11] LI X, MA H. Hypoenergetic and strongly hypoenergetick-cyclic graphs[J]. MATCH Commun Math Comput Chem, 2010 (64): 41-60.
[12] ENGLAND W, RUEDENBERG K. Why is the delocalization energy negative and why is it proportional to the number of electrons?[J]. J Am Chem Soc, 1973 (95): 8769-8775.
[13] MAJSTOROVIC S, KLOBUCAR A, GUTMAN I. Selected topics from the theory of graph energy: Hypoenergeticgraphs[J]. Applications of Graph Spectra, 2009 (1): 65-105.
[14] LI X, MA H. All connected graphs with maximum degree at most 3 whose energies are equal to the number of vertices[J]. MATCH Commun Math Comput Chem, 2010 (64): 7-24.
[15] GONG S C, LI X, XU G H, et al. Borderenergetic graphs[J]. MATCH Commun Math Comput Chem, 2015 (74): 321-332.
[16] TURA F.L-borderenergetic graphs[J]. MATCH Commun Math Comput Chem, 2017 (77): 37-44.
[17] DENG B, LI X. More onL-borderenergetic graphs[J]. MATCH Commun Math Comput Chem, 2017 (77): 115-127.
[18] DENG B, LI X, WANG J. Further results onL-borderenergetic graphs[J]. MATCH Commun Math Comput Chem, 2017 (77): 607-616.
[19] DENG B, LI X. OnL-borderenergetic graphs with maximum degree at most 4[J]. MATCH Commun Math Comput Chem, 2018 (79): 303-310.
[20] LI X, WEI M, GONG S. A computer search for the borderenergeticgraphs of order 10[J]. MATCH Commun Math Comput Chem, 2015 (74): 333-342.
[21] SHAO Z, DENG F. Correcting the number of borderenergetic graphs of order 10[J]. MATCH Commun Math Comput Chem, 2016 (75): 263-266.
[22] DENG B, LI X, GUTMAN I. More on the borderenergetic graphs[J]. Lin Algebra Appl, 2016 (497): 199-208.
[23] HOU Y, TAO Q. Borderenergetic threshold graphs[J]. MATCH Commun Math Comput Chem, 2016 (75): 253-262.
[24] LI X, WEI M, ZHU X. Borderenergetic graphs with small maximum or large minimum degrees[J]. MATCH Commun Math Comput Chem, 2016 (77): 25-36.
[25] DAS K C, MOJALLAL S A, GUTMAN I. On Laplacian energy in terms of graph invariants[J]. Appl Math Comput, 2015 (259): 470-479.
