躺滴法测量干湿循环条件下土壤固-液接触角的滞后特性

杨 松，马泽慧，王 磊，罗茂泉



躺滴法测量干湿循环条件下土壤固-液接触角的滞后特性

杨 松，马泽慧，王 磊，罗茂泉

（云南农业大学水利学院，昆明 650201）

接触角滞后是使土壤的土水特征曲线产生滞后现象的主要因素之一，而土水特征曲线的滞后特性是土壤干湿循环的显著特征。该文采用混合制样法制备不同接触角的土样，通过躺滴法对干湿循环过程中土体的固-液接触角随时间的变化关系进行测量，结果表明：随着土样表面固滴的蒸发，其固-液接触角是不断减小的，且初始接触角越大，固滴完全蒸发所用的时间越长，黏土接触角随时间变化关系曲线呈线性，而砂土的则表现出一定的非线性。不论土体的初始接触角多大，临近固滴蒸发结束，接触角都会变为0，且整个蒸发过程中固-液-气三相接触线不发生移动，固-液接触面积保持不变。试验结果证实了土壤脱湿过程把固-液接触角假设为0是合理的，并且可以断定接触角滞后特性也可能是非饱和土土水特征曲线在反复干湿循环下滞回圈不断减小的原因之一。

土壤；接触角；滞后；非饱和土壤；干湿循环

0 引 言

作为三相介质的非饱和土，固-液接触角（以下简称接触角）是影响其物理力学性质的重要因素之一[1]。目前对接触角的研究主要集中在表面物理化学领域，并且研究对象基本为宏观状态下具有较大连续表面的固体材料[2]。耕作层土壤由于受有机物影响会导致土壤斥水，即土颗粒与孔隙水间的接触角增大，并且带来一系列的农业问题及环境地质问题，因此土壤学及水文地质学也开始对松散堆积物中的接触角展开研究，并且不断深入[3-8]。岩土工程领域近年来也开始关注土颗粒的接触角。William等[9]把土颗粒视为理想的等直径球体颗粒，计算出了土体吸湿过程中接触角增大导致的正、负孔隙水压力的分界区域。栾茂田等[10]考虑接触角的变化，建立了非饱和土的理论土水特征曲线。张昭等[11]把土颗粒简化为不等直径的球体颗粒，颗粒间由圆环状液桥连接，在此基础上研究了接触角、液桥体积和颗粒半径比对毛细力与颗粒间距的无量纲关系的影响。接触角对非饱和土中基质吸力的影响也得到了试验验证[12]。

对于非理想固体表面，接触角并不是一个固定值，而是存在一个变化区间，即：接触角滞后特性，这也是导致土水特征曲线出现滞回现象的一个重要原因[13]。很多学者都建立了相应的土水特征曲线模型，并且对模型参数赋予物理意义[14-16]，Zhou[17]建立了考虑接触角因素的土水特征曲线模型，模型假设后退接触角为0，仅把前进接触角作为模型参数之一，然而前进接触角的大小是通过分析误差得出，并没有进行试验测试。很多涉及非饱和土毛细力的模型也都是在假定接触角的基础上进行计算分析，接触角的变化范围及变化模式都是参考连续固体[10-11,18-19]，而干湿循环对大部分连续固体的影响是可以忽略的[20]。

本文采用混合十八胺搅拌法改变土颗粒与孔隙水的接触角，在此基础上设计了躺滴法测量干湿循环过程中土体接触角变化的试验，希望能为进一步研究非饱和土的微观机制提供相应的试验基础。

1 试验材料与方法

1.1 土样的基本性质

分别采用黏土和砂土进行相应的试验测试，其中黏土取自云南省昆明市境内昆曲高速公路严家山段，液限为41%，塑限为20.3%。砂土取自云南省昆明市境内的团结乡。土样取回后风干、碾碎，并过1 mm的筛备用，2种土样的颗分曲线如图1所示。

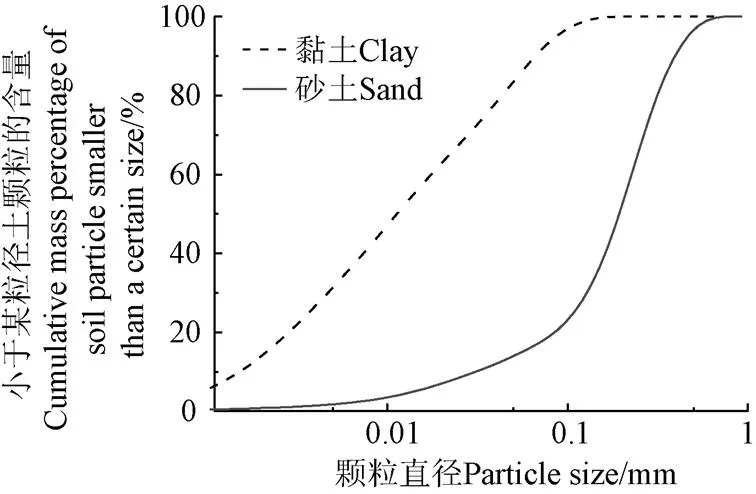
图1 黏土和砂土的颗分曲线

1.2 不同接触角土样的制备

为制备接触角不断变化的土样，本文采用混合搅拌法制样。采用的斥水剂为十八胺，十八胺为白色蜡状粉末，具有强烈的斥水性，其熔点为52.3 ℃，沸点232 ℃，不溶于水，具有胺的通性。土壤的斥水性随着十八胺含量的增大会不断增加，因此很多学者在室内试验中采用混合十八胺的方法增加土壤的斥水性[6,8]。具体步骤如下：把筛好的土样加入粉末状的十八胺（C18H39N），为保证十八胺在土壤中分布均匀，搅拌均匀后放入烘箱内在80 ℃下持续烘烤8 h，其间每隔2 h把土样取出并保持温度70 ℃以上搅拌土样5 min，这样可以保持十八胺处于液态，并且在土壤中均匀分布，烘好的土样在室内放置冷却后进行接触角测量试验，用十八胺处理后的土壤具有很好的斥水性。图2为十八胺含量为0.4%的砂土表面的液滴形态，很显然，此时的液滴与土壤的接触角大于90°。砂土和黏土各准备4种不同比例十八胺的混合样，十八胺含量分别为：0.1%、0.2%、0.4%。以符号“S”代表砂土、“N”代表黏土，下标为十八胺含量，如：十八胺含量为0.2%的黏土以符号：N0.2表示，其余符号以此类推。

图2 十八胺含量为0.4%时砂土表面的液滴

1.3 躺滴法测量干湿循环过程中的接触角

躺滴法是测量液体与连续固体表面接触角的一种最常规的方法[2]。Bachmann等[21]把单层土颗粒粘附于连续固体的表面，再用躺滴法测量斥水性土壤的接触角，通过接触角来评价土壤的斥水程度。本文试验参照Bachmann等[21]的方法进行，制作试样的具体步骤如下：取长度为4cm左右的双面胶带贴到载玻片上，将准备好的土颗粒均匀覆盖载玻片，并用质量为200 g的砝码压住载玻片，持续时间为2 min，移开砝码后反复轻轻磕碰载玻片以去除多余的土颗粒，直到胶带表面覆盖有一层薄薄的土颗粒，且土颗粒分布均匀无明显凸起，为保证液滴在相同的环境下进行蒸发，试验过程中均保持温度为24 ℃，相对湿度为45%。

接触角测量试验在JC2000型接触角测量仪上进行。躺滴法测量接触角的步骤如下：把制作好的载玻片样品放到测试台上，在微量进样器中抽入去离子水，把进样器固定在仪器自动注液仪上，自动注样5L后液体在注样器针尖产生悬滴，同时注样器针尖向下移动，悬滴与载玻片表面接触，并在土颗粒覆盖的载玻片表面形成一滴小液滴。通过光学放大系统和图像采集系统获取液滴的外形，并测量接触角的大小，此时得到的接触角是介于土颗粒前进接触角和后退接触角之间的表观接触角。

为模拟非饱和土干湿循环过程，并测量干湿循环过程中的接触角，本文增加了以下试验步骤：当悬滴与土颗粒覆盖的载玻片表面接触并形成固着液滴（固滴1）时，让液滴在常温下持续蒸发，测量接触角随时间的变化关系，当液滴完全蒸发结束后保持载玻片位置不变，用微量进样器在原来位置注入10L液体，形成比固滴1更大的固-液接触面，等待液滴蒸发结束（通过光学放大系统看不到液滴，但在基底上可以看到土颗粒微微的湿润痕迹，如：图3所示），再通过微量进样器在原位置注入5L去离子水，形成固滴2，固滴2的三相接触线在湿润痕迹范围内，测量固滴2的接触角随时间的变化关系，直到固滴2完全蒸发结束。把试样在室内静置24 h，再重复测量固滴1的步骤，此时载玻片上的液滴记为固滴3，每个固滴接触角需要测3个平行样取平均值作为其最终值。以N0.2试样表面的固滴1、固滴2、固滴3为例，其初始形态如图4所示。

图3 S0.1试样表面液滴蒸发结束后表面的湿润痕迹

图4 N0.2土样表面的固滴1、固滴2、固滴3

2 试验结果

固滴1的接触角测量试验是在试样烘干冷却后进行，此时的试样含水率接近于0，测出的接触角是试样处于基本干燥时的接触角。固滴2的接触角是在土颗粒表层覆盖水膜，但土颗粒间没有形成液桥的情况下进行的，而固滴3则是土颗粒中的自由水处于完全蒸发状态时的接触角。3个液滴的初始接触角反映了土体干湿循环不同的起始状态下的接触角，而接触角随时间的变化则反映了土体退湿过程中的接触角，固滴1对应的土颗粒表层的水膜最薄，固滴3次之，固滴2对应的水膜最厚。

2.1 接触角随时间变化

固滴蒸发过程中接触角随时间变化关系如图5所示，具体公式见表1。通过十八胺改性的黏土和砂土，其初始接触角都随着十八胺的含量的增加而增大。N0.1、N0.2和N0.4的初始接触角为：70°、75°、106°；S0.1、S0.2和S0.4的初始接触角为：105°、115°、125°。相同的十八胺含量砂土的接触角要明显大于黏土的接触角，这主要与土颗粒的几何形状有关[22]。

图5 固滴蒸发过程中接触角随时间变化

表1 固滴接触角拟合结果

所有土样中，土颗粒与孔隙水的接触角在蒸发过程中是不断减小的，直到接触角变为0；同种土样，固滴体积相同时，固滴1完全蒸发所用的时间要长于固滴2和固滴3，固滴2和固滴3完全蒸发所用的时间比较接近，但固滴3完全蒸发所用的时间要略微长于固滴2，表明土颗粒的初始接触角会影响土体的蒸发速率。特别需要注意的是，所有试样在蒸发过程中均保持固-液接触面积不变（固滴的初始半径0不变），直到固滴完全蒸发。表1给出了接触角随时间变化关系的拟合结果，其中黏土样用直线方程拟合，除黏土N0.2样的固滴3外，其余黏土样的2均为0.98以上，大部分达到0.99，而砂土样用抛物线方程进行拟合，除S0.3样固滴3的2为0.9853，其余试样2均大于0.99，这表明液滴完全蒸发，黏土样的固-液接触角随时间的变化关系呈线性关系而砂土的则表现出一定的非线性。

2.2 干湿循环过程中的接触角与固-液接触面

固滴1、固滴2和固滴3的初始接触角如图6所示，从图中可以看出，无论是黏土样还是砂土样，固滴1的接触角都大于固滴2和固滴3，黏土样中，N0.1、N0.2和N0.4的固滴1和固滴2分别相差：25°、45°和51°；砂土样中S0.1、S0.2和S0.4的固滴1和固滴2分别相差：30°、39°和20°。黏土样随着接触角的增大，固滴1和固滴2的接触角差值是不断增大的，而砂土并没有这个规律，初始接触角最大的S0.4中固滴1和固滴2的接触角差值反而是最小的，只有20°，但值得注意的是此时S0.4样固滴1、固滴2和固滴3的3个初始接触角均大于90°。固滴3和固滴2差值最小的为S0.1样的5°，差值最大的为N0.2样的10°。这些接触角之间的差值，都是由于接触角滞后引起的，且土颗粒的接触角滞后还与其干湿循环的初始状态有关。

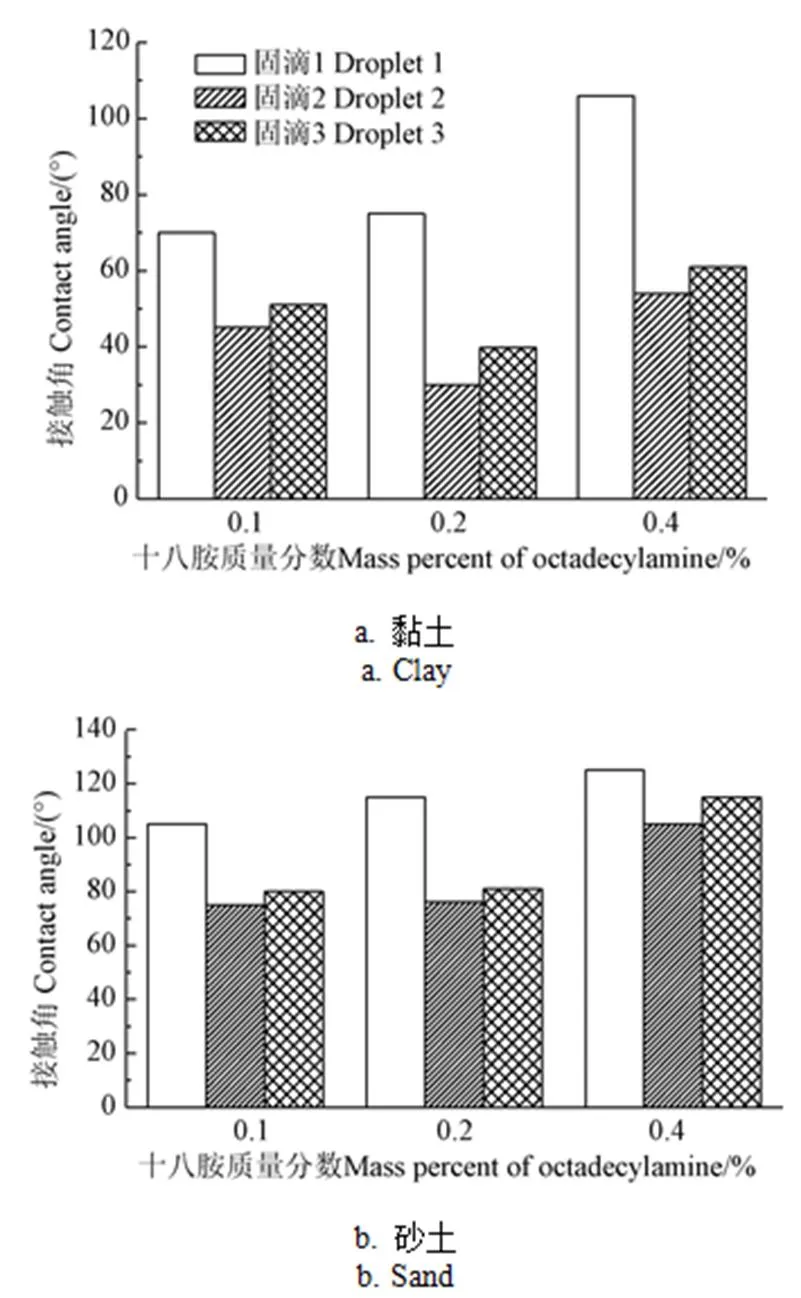
图6 固滴的初始接触角

3 讨 论

3.1 土颗粒蒸发过程的接触角变化模式

固滴在连续固体表面蒸发模式一般分为3个阶段[23-25]，第一阶段：固滴的初始阶段，此时固滴的接触角为初始接触角0，固滴没有蒸发。第二阶段：钉扎阶段，固滴开始蒸发，随着固滴体积的减小，其接触角在不断减小（θ减小），但三相接触线保持不动，固-液接触面积保持为常数（0不变）。第三阶段：滑移阶段，当接触角减小到一定值（即：后退接触角），接触角保持不变，三相接触角开始滑动，固液接触面积不断减小直到固滴完全蒸发。

在本次试验中，无论土体的接触角多大，土颗粒表面固滴在蒸发过程都只出现前2个阶段而缺失第三阶段，即：土体的接触角在整个蒸发过程中不断减小，并且保持固液接触面积不变，直到接触角减小为0。这个试验结果对利用理想球体颗粒计算和分析非饱和土颗粒之间的微观力学特性很有意义，通常当土体的含水率比较小，土体处于水封闭状态[26]，此时可以用由液桥连接的球体颗粒来模拟土体的微观特性[27]，这种情况下模拟土中含水率变化主要通过保持接触角不变增大固液接触面积来实现，但这与试验结果不符，根据试验结果，液桥断裂之前应该是保持固液接触面积不变；水封闭状态下的非饱和土含水率改变主要是由于蒸发过程中接触角减小造成的。

所有土样的接触角变化幅度都很大，不论土样的初始接触角多大，固滴快要完全蒸发时接触角最后都会减小为0，S0.4的接触角甚至从125°变为0，虽然0不一定等于土颗粒表面的后退接触角，但对于蒸发式退湿[28]，在土水特征曲线的边界干燥曲线中假定接触角为0和试验结果是一致的。

3.2 土壤干湿循环过程中的接触角因素

非饱和土土水特征曲线存在明显的滞回特性，即在经过一个吸力变化循环后，土中含水率的变化不可恢复[29]，接触角滞后是造成滞回现象的主要原因之一。非饱和土经过多次干湿循环后滞回圈会不断减小[30]，而这其中可能也有接触角滞后的因素，本文设计的反映干湿循环的固滴蒸发试验，同一土样的相同位置，仅仅是因为土颗粒表面覆盖的水层（结合水）厚度不同，其接触角就会不同，且表层水膜越厚其接触角越小，而已有的试验结果表明接触角对非饱和土中的基质吸力有重要影响[12]，因此，土水特征曲线反复干湿循环存在滞回圈减小的现象，其中也有接触角的因素。

当然，土壤干湿循环中除了接触角这个影响孔隙水几何形态的因素外，还包括温度和湿度，温度和湿度的变化必然会导致土壤水分蒸发速率的变化，而这其中会给接触角滞后带来的影响，还有待进一步深入研究。

4 结 论

1）非饱和土壤的接触角随着固滴的蒸发，其接触角是不断减小的，且初始接触角越大，固滴完全蒸发所用的时间越长。黏土接触角随时间变化关系曲线呈线性，而砂土的则表现出一定的非线性。

2）连续固体表面液滴蒸发一般存在3个阶段：初始阶段，钉扎阶段和滑移阶段。而土颗粒表面的蒸发模式只存在初始阶段和钉扎阶段，没有滑移阶段，即：不论土体的初始接触角多大，固滴蒸发快结束时，接触角都会变为0，且整个蒸发过程中固-液-气三相接触线不发生移动，固液面积保持不变。

3）干湿循环对接触角有重要影响，土颗粒的表层水膜越薄接触角越大，水膜越厚接触角越大，直到土体进入水封闭状态，这也可能是非饱和土土水特征曲线在反复干湿循环下滞回圈不断减小的原因之一。

[1] 卢宁，William J Likos，力科思，等. 非饱和土力学[M]. 北京：高等教育出版社，2012.

[2] 沈钟，赵振国，康万利. 胶体与表面化学[M]. 北京：化学工业出版社，2012.

[3] Czachor H, Doerr S H, Lichner L. Water retention of repellent and subcritical repellent soils: New insights from model and experimental investigations[J]. Journal of Hydrology, 2010, 380: 104－111.

[4] Woche S K, Goebel M O, Kikham M B, et al. Contact angle of soils as affected by depth, texture, and land management[J]. European Journal of Soil Science, 2005, 56(2): 239－251.

[5] Vogelmann E S, Reichert J M, Prevedello J, et al. Threshold water content beyond which hydrophobic soils become hydrophilic: The role of soil texture and organic matter content[J]. Geoderma, 2013(209/210): 177－187.

[6] 刘春成，李毅，任鑫，等. 四种入渗模型对斥水土壤入渗规律的适用性[J]. 农业工程学报，2011，27(5)：62－67.

Liu Chuncheng, Li Yi, Ren Xin, et al. Applicability of four infiltration models to infiltration characteristics of water repellent soils[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2011, 27(5): 62－67. (in Chinese with English abstract)

[7] 商艳玲，李毅，朱德兰. 再生水灌溉对土壤斥水性的影响[J]. 农业工程学报，2012，28(21)：89－97.

Shang Yanling, Li Yi, Zhu Delan. Effects of reclaimed water irrigation on soil water repellency[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(21): 89－97. (in Chinese with English abstract)

[8] 陈俊英，吴普特，张智韬，等. 土壤斥水性对含水率的响应模型研究[J]. 农业机械学报，2012，43(1)：63－67.

Chen Junying, Wu Pute, Zhang Zhitao, et al. Response models for soil water repellency and soil moisture[J]. Transactions of the Chinese Society for Agricultural Machinery, 2012, 43(1): 63－67. (in Chinese with English abstract)

[9] William J L, Ning L. Hysteresis of capillary stress in unsaturated granular soil[J]. Journal of Engineering Mechanics, ASCE, 2004, 130(6): 646－655.

[10] 栾茂田，李顺群，杨庆. 非饱和土的理论土—水特征曲线[J]. 岩土工程学报，2005，27(6)：611－615.

Luan Maotian, Li Shunqun, Yang Qing. Theoretical soil-water characteristic curve for unsaturated soils[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(6): 611－615. (in Chinese with English abstract)

[11] 张昭，刘奉银，齐吉琳，等. 考虑固-液接触角影响的粗颗粒间液桥毛细力计算方法[J]. 水利学报，2016，47(9)：1197－1207.

Zhang Zhao, Liu Fengyin, Qi Jilin, et al. A calculation method for the capillarity force of the liquid bridge between coarse particles considering the effect of solid-liquid contact angle[J]. Journal of Hydraulic Engineering, 2016, 47(9): 1197－1207. (in Chinese with English abstract)

[12] 杨松，龚爱民，吴珺华，等. 接触角对非饱和土中基质吸力的影响[J]. 岩土力学，2015，36(3)：674－678.

Yang Song, Gong Aimin, Wu Junhua, et al. Effect of contact angle on matric suction of unsaturated soil[J]. Rock and Soil Mechanics, 2015, 36(3): 674－678. (in Chinese with English abstract)

[13] Pham H Q, Fredlund D G, Barbour S L. A study of hysteresis models for soil-water characteristic curves[J]. Canadian Geotechnical Journal, 2005, 42(6): 1548－1568.

[14] 汪时机，程明书，李贤，等. 非饱和土双应力变量广义土水特征曲线理论模型构建[J]. 农业工程学报，2017，33(6)：1－7.

Wang Shiji, Cheng Mingshu, Li Xian, et al. Establishment of generalized soil-water characteristic curve theoretical model considering two stress state variables for unsaturated soils[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(6): 1－7. (in Chinese with English abstract)

[15] 张昭，刘奉银，赵旭光，等. 考虑应力引起孔隙比变化的土水特征曲线模型[J]. 水利学报，2013，44(5)：578－585.

Zhang Zhao, Liu Fengyin, Zhao Xuguang, et al. A soil water characteristic curve model considering void ratio variation with tress[J]. Journal of Hydraulic Engineering，2013, 44(5): 578－585. (in Chinese with English abstract)

[16] 程明书，李贤，汪时机，等. 非饱和土双应力变量广义土水特征曲线理论模型验证[J]. 农业工程学报，2017，33(6)：8－16.

Cheng Mingshu, Li Xian, Wang Shiji, et al. Vertification of generalized soil-water characteristic curve model considering two stress state variables for unsaturated soils[J]. Transactions of the Chinese Society for Agricultural Machinery (Transactions of the CSAE), 2017, 33(6): 8－16. (in Chinese with English abstract)

[17] Zhou A N. A contact angle-dependent hysteresis model for soil–water retention behaviour[J]. Computers & Geotechnics, 2013, 49(4): 36－42.

[18] Yang S, Lu Tinghao. Study of soil-water characteristic curve using microscopic spherical particle model[J]. Pedosphere, 2012, 22(1): 103－111.

[19] 张昭，刘奉银，李荣建，等. 黏土颗粒间液桥从形成至断裂时毛细力的演化规律[J]. 岩土力学，2016，37(10)：2845－2850.

Zhang Zhao, Liu Fengyin, Li Rongjian, et al. Evolution of capillary force of liquid bridge between clay particles in process from its formation to rupture[J]. Rock and Soil Mechanics, 2016, 37(10): 2845－2850. (in Chinese with English abstract)

[20] 赵亚溥. 表面与界面物理力学[M]. 北京：科学出版社，2012.

[21] Bachmann J, Ellies A, Hartge K H. Development and application of a new sessile drop contact angle method to assess soil water repellency[J]. Journal of Hydrology, 2000, 231(10): 66－75.

[22] 杨松，吴珺华，董红艳，等. 砂土和黏土的颗粒差异对土壤斥水性的影响[J]. 土壤学报，2016，53(2)：421－426.

Yang Song, Wu Junhua, Dong Hongyan, et al. Effects of particle differences between sands and clay on soil water repellency[J]. Acta Pedologica Sinica, 2016, 53(2): 421－426. (in Chinese with English abstract)

[23] Bourgesmonnier C, Shanahan M E R. Influence of evaporation on contact angle[J]. Langmuir, 1995, 11(7): 2820－2829.

[24] Birdi K S, Vu D T, Winter A. A study of the evaporation rates of small water drops placed on a solid surface[J]. Journal of Physical Chemistry, 1989, 93(9): 3702－3703.

[25] Shanahan M E R, Bourgès C. Effects of evaporation on contact angles on polymer surfaces[J]. International Journal of Adhesion & Adhesives, 1994, 14(3): 201－205.

[26] 俞培基，陈愈炯. 非饱和土的水-气形态及其与力学性质的关系[J]. 水利学报，1965(1)：16－23.

Yu Peiji, Chen Yujiong. Water-air patterns and mechanics properties of unsaturated soil[J]. Journal of Hydraulic Engineering, 1965(1): 16－23. (in Chinese with English abstract)

[27] 李顺群. 非饱和土的吸力与强度理论研究及其试验验证[D]. 大连：大连理工大学，2006.

Li Shunqun. Study on Suctions and Shear Strength of Unsaturated Soils and Experimental Verification[D]. Dalian: Dalian University of Technology, 2006. (in Chinese with English abstract)

[28] 杨松，吴珺华，黄剑峰，等. 接触角对张力计及轴平移技术测量非饱和土吸力的影响[J]. 岩石力学与工程学报，2016(增刊1)：3331－3336.

Yang Song, Wu Junhua, Huang Jianfeng. Effects of contact angle on suction measurement with tensiometers and axis-translation technique in unsaturated soils[J]. Chinese Journal of Rock Mechanics and Engineering, 2016(Supp.1): 3331－3336. (in Chinese with English abstract)

[29] Topp G C. Soil water hysteresis in silt loam and clay loam soils[J]. Water Resources Research, 1971, 7(7): 914－920.

[30] 张雪东，赵成刚，刘艳，等. 土水特征曲线（SWCC）的滞回特性模拟研究[J]. 工程地质学报，2010，18(6)：920－925.

Zhang Xuedong, Zhao Chenggang, Liu Yan, et al. Simulation and hysteresis model for soil-water characteristic curves[J]. Journal of Engineering Geology, 2010, 18(6): 920－925. (in Chinese with English abstract)

Hysteresis characteristics of soil solid-liquid contact angle measured by sessile drop method during wetting-drying cycles

Yang Song, Ma Zehui, Wang Lei, Luo Maoquan

(,650201,)

The contact angle hysteresis is one of the main causes of soil water characteristic curve (SWCC) hysteresis in unsaturated soil, the hysteresis of SWCC is a remarkable feature of soil under wetting and drying cycles. In this study, we prepared soil samples with different contact angles by adding repellent agents (octadecylamine) and found that the more the content of the water repellent agents, the greater the contact angle between the soil particles and the pore water. Contact angle measurement test were designed at the same time, drying-wetting cycles of soil were reflected in the test. Droplet 1 was the initial state of the droplet, droplet 2 was a little drop formed after droplet 1 evaporation immediately, and droplet 3 was a little drop formed 24 hours after droplet 2 evaporation. The test results showed that, the contact angles of sand were greater than the clay with the same water repellent agents content, this was mainly because of the geometrical shapes of the soil particles. In all of the soil samples, the contact angles of soil particles and the pore water decreased continuously during the evaporation process, until the contact angle became 0. At this time, the droplets were completely vaporized. The change of the contact angle on clay surface had a linear relation with time, but it was a nonlinear on sand surface. In the same samples, the evaporation time of droplet 1 was longer than droplet 2 and droplet 3 with the same liquid volume, the time spent in droplet 2 and droplet 3 complete evaporation was relatively close, but droplet 3 took a little more time to evaporation than droplet 2, this meant initial contact angle may affect the evaporation velocity of the soil. The larger the initial contact angle, the longer the evaporation time of the droplet would be. Either sand or clay, the contact angle of droplet 1 was greater than droplet 2 and droplet 3. This was because that the contact angle of droplet 1 was measured on the fully dry sample surface. The contact angle of droplet 2 was measured on the sample surface when soil particles were covered by water films from the droplet 1. The contact angle of droplet 3 was measured on the state in which the free water was evaporated completely. The initial contact angle of the three droplets reflected the contact angle of the soil under different initial conditions of wetting drying cycles. The water films of soil particles which the droplet 1 correspond to were the thinnest and droplet 2 correspond to be the thickest. There were three stages of droplet evaporation on a continuous solid surface：Initial stage, pinning stage and slipping stage. The evaporation mode of soil particles only existed in the initial stage and pinning stage, and there was no slip stage. That was, no matter how lager the initial soil contact angle was, by the end of the droplet evaporation, contact angle would be 0. In the whole evaporation process, the three-phase contact line did not move, and the solid-liquid area remained unchanged. The experiment confirmed that it was reasonable to suppose the contact angle was zero during soil drying, the contact angle hysteresis was one of the reasons why SWCC hysteresis loops became small during wetting-drying cycles.

soils; contact angle; hysteresis; unsaturated soil; wetting-drying cycles

10.11975/j.issn.1002-6819.2018.02.015

S152

A

1002-6819(2018)-02-0114-06

2017-08-15

2017-12-28

国家自然科学基金项目（41662021，51209182）

杨 松，副教授，博士，主要从事非饱和土基本性质研究。 Email：yscliff007@126.com

杨 松，马泽慧，王 磊，罗茂泉. 躺滴法测量干湿循环条件下土壤固-液接触角的滞后特性[J]. 农业工程学报，2018，34(2)：114－119. doi：10.11975/j.issn.1002-6819.2018.02.015 http://www.tcsae.org

Yang Song, Ma Zehui, Wang Lei, Luo Maoquan. Hysteresis characteristics of soil solid-liquid contact angle measured by sessile drop method during wetting-drying cycles[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(2): 114－119. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2018.02.015 http://www.tcsae.org