因子分解机应用

张华南

摘要

本文结合支持向量机（Support Vector Machines，縮写为SVM）的优点，介绍了一种新的用于因子分解的模型一因子分解机（Factorization Machines，缩写为FM）。与SVM相似，FM针对特征向量给出综合预测。与SVM相比，FM使用分解的因子参数，在变量中对交互行为建模，甚至在SVM无法解决的稀疏性（如推荐系统）等问题中，FM也可以用于评估交互行为通过在线性时间中计算FM模型方程式，可以直接优化FM。不像非线性的SVM，FM不需要转换，模型参数可以直接估计出来，而不用任何支持向量。

【关键词】因子分解 特征向量 稀疏性 推荐评估

在机器学习和数据挖掘中常用支持向量机做推荐和预测。然而，在协同过滤向量机没有很好的模型直接应用标准矩阵和张量分解模型。标准支持向量机预测不成功的原因是在非线性复杂的稀疏数据下使用不可靠的参数。张量分解模型的缺点是不适用标准预测数据。为此，引入一个新的预测模型分解机（FM），具有一般预测向量机特征，能够在高稀疏数据下可靠估计参数。

FM有以下三个优点：

（1）FM允许数据稀疏情况下估计和预测任务。

（2）FM具有线性复杂度，不依赖支持向量机等向量。

（3）FM适用于普遍预测，可以用于任何有价值的特征向量，FM可以模拟最先进的模型如：SVD++，PITF或FPMC。

1 稀疏问题中的预测

预测任务是一个估计函数y：Rⁿ→T，真实特征值向量x∈Rⁿ目标域为T（例如，T=R用以回归或T={+，-}用以分类）。在半监督学习电假设存在训练集D={x^（1），y^（1），（x^（2），y^（2），…}，用作目标函数y的样例。在排序任务中，即函数y和目标T=R可以用来对特征向量X打分，并根据分值排序。也可以用成对的训练数据来学习打分功能，特征元组（x^A，y^B）∈D代表x^（A）的排名高于x^B。如果成对的排序关系不对称，就仅仅利用正向的训练实例。

本文解决的是x极其稀疏的问题。例如，向量集X中几乎全部元素x₁都为0。在特征向量X中，设m（X）为非零元素的数量，对于所有的向量X∈D，其非零元素m（X）的平均数为石口。在许多真实世界里的数据，诸如事件事务（如推荐系统中的购买行为）和文本分析（如词袋算法）等都存在有巨大的稀疏性（mD<

假设在旅游景点评论系统中存在这样的事务数据，系统记录下用户u∈U在某个特定的时间t∈R对旅游景点i∈I打分，分值r∈{1，2，3，4，5}设用户集U和旅游景点线路集I为：

已有的观察数据S为：

本次预测任务是基于该数据，用估计函数y来预测在未来的某个时间点用户对旅游景点的评分行为。

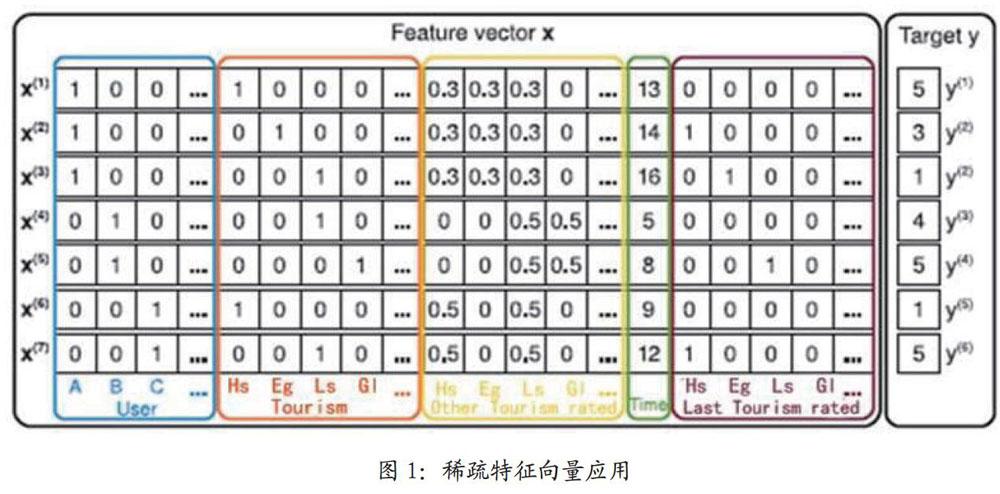
图1稀疏特征向量X实例。每一行代表一个特征向量x^（i）及其相应的目标y^（i）。前4列（蓝）代表当前用户的指标变量;接下来的5列（红）代表目标项的指标变量。再往后5列（黄）代表附加的隐性指标（即用户给其它旅游景点的评分）。一列特征（绿）代表以月为单位的时间。最后的5列（棕）为用户在目标项之前给出评分的最近旅游景点。最右一列为目标函数，此处为旅游景点的评分。

图1展示了本次任务中如何从S中提炼特征向量的例子。首先，存在|U|二分指标变量（蓝框），代表某次事务的活跃（当前）用户，假定每次事务（u，i，t，r）∈s一定存在一位活跃（当前）用户，例如，用户Alice（A）在第一行（x_A^（1）=1）。后一个二分指标变量（红框）|I|代表活跃（当前）目标项，一定存在一个活跃项（e.g.x_T1^（1）=1）。图1中的特征向量也包括指标变量（黄框），用来表示用户己评分的其它所有旅游景点。对于每个用户，变量范化后的和为1，例如，Alice对Huanshan（黄山）、Enshidxg（恩施大峡谷）和Lushan（庐山）评过分。另外，样例包括一个变量（绿框）代表从2015年3月份开始（至评论点）的时间。最后的棕色框内的向量代表用户在评论当前信息之前的上一次评论过的旅游景点信息，例如，Alice在评论Enshidxg之前评论过Huanshan。

2 因子分解机

2.1 因子分解机模型

在因子分解机的度d=2时，模型公式定义如下：

其中，需要估计的模型的参数有：

并且，<.，.>表示大小为k的两个向量作点乘：

V中的一排v₁描述了k个系数下第i个变量。k∈N₀⁺表示超平面参数，用于定义因子分解的维数。

A双路[2-way]FM（度d=2）表示变量之间所有单独的和成对的相互作用：

w₀是全局偏差

w_i表示第i个变量的力度

w_i，j=（v_i，v_j）表示第i个变量和第j个变量之间的相互作用。在对相互作用建模时，FM模型对每个相互作用没有使用自身模型中的参数w_i，j∈R，而是将其因子分解。在后面将会看到，当数据稀疏时，这正是高位交互（d>=2）的参数估计产生高质量参数的关键点。

2.2 因子分解机

FM閉合模型公式的计算为线性。因此FM模型参数（w0，w，V）可以用梯度下降法来高效学习一例如随机梯度下降法（SGD），有大量的损失函数可供选择，如平方损失函数，logit损失函数和hinge损失函数。FM模型的梯度为： 总和独立于i，可以计算y（X）0通常，每一梯度的计算可以在持续时间O（1）内完成。所有的参数校正在实例（x，y）中能在O（kn）内完成，稀疏的情况下为O（km（x））。

3 结语

FM汇集向量机的通用性与分解模型的好处：FM能够在高稀疏问题中预测;模型方程是线性的，只依赖于模型参数;FM是普遍预测，可以处理任何真正价值向量。另一方面，还有其它很多不同的因子分解模型，如矩阵分解，平行（相似）因子估计或特殊的模型如SVD++，PITF，FPMC等。这些模型的缺点在于不适用于通用的预测任务，而仅仅能处理特定的数据。另外，这些模型的公式和优化算法只能单独解决各自领域的个别问题。FM仅在处理输入数据（如特征值）的时候模仿这些方法。FM在因子分解模型中可适用于普通用户。

参考文献

[1]S.Balakrishnan and S.Chopra.Collaborative ranking.In WSDM，pages143-152，2012.

[2]S.Rendle and L.Schmidt-Thieme.Pairwise interaction tensorfactorization for personalized tagrecommendation.In WSDM，pages 81-90，2010.

[3]J.Weston，C.Wang，R.We iss，andA.Berenzweig.Latent collaborativeretrieval.In ICML，2012.

[4]S.-H.Yang，B.Long，A.Smola，N.Sadagopan，Z.Zheng，and H.Zha.Like likealike：joint friendship and interestpropagation in social networks.InWWW，pages 537-546，2014.

[5]L.Zhang，D.Agarwal，and B.-C.Chen.Generalizing matrix factorizationthrough flexible regression priors.In Recsys，pages 13-20，2014.

[6]J.Zhu and E.P.Ring.Sparse topicalcoding.In UAI，pages 831-838，2011.