三维向量空间中线性变换的特征向量的几何意义*
2014-12-25纪永强
纪永强
(湖州师范学院 理学院,浙江 湖州313000)
0 引 言
关于线性变换的特征向量的定义及有关性质,在文献[1~3]中都有讨论.文献[4]给出了平面上线性变换的特征向量的几何意义.对于空间中线性变换的特征向量的几何意义还没有人具体研究过,本文给出了它们的几何意义,对特征向量有了直观的认识.
1 空间R3 中非对称矩阵对应的线性变换的特征向量的几何意义

其中:x=(x1,x2,x3)∈R3;∈R3.R3中的元素(x1,x2,x3)也是空间中某点的坐标,因此称R3是空间.设F:R3→R3是空间R3中的线性变换,即
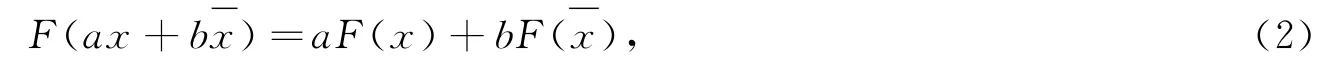
其中:x,x∈R3;a,b∈R.由文献[1]中的定理1.2.2得如下定理成立.
定理[1]设F:R3→R3为F((x1,x2,x3))=(y1,y2,y3),则F是空间R3中的线性变换的充要条件是:

即

由此可知,空间R3中的线性变换F与三阶实矩阵A=(aij)3×3是相互确定的,即给出了线性变换就可得出矩阵A,反之给出了矩阵A就可写出线性变换.
线性变换的几何意义是:设A的行列式,则线性变换(3)式是空间R3中非退化的线性变换,它将空间R3中的点(x1,x2,x3)变为唯一的一点,此点的坐标是:
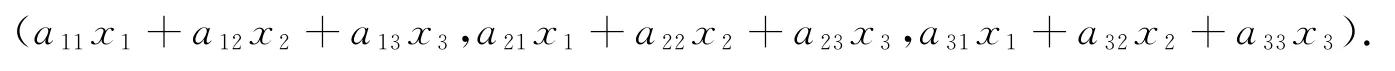

其中:(a11,a21,a31),(a12,a22,a32)和(a13,a23,a33)分别是向量F(e1),F(e2)和F(e3)关于基e1,e2,e3的坐标.(5)式写成矩阵形式是:

设α=(x1,x2,x3)∈R3,则α可写成矩阵形式:

从而有:

因为F是R3上的线性变换,由(2)式、(6)式及(7)式得:

由文献[2]得特征向量的定义如下:
定义[2]设F:R3→R3是向量空间R3上的线性变换,λ∈R,α是R3上的非零向量,若

则称λ是线性变换F的一个特征根,α属于特征根λ的特征向量.
对任意a∈R,a≠0,有F(aα)=λ(aα),所以aα是属于特征根λ的所有特征向量.因为α=(x1,x2,x3)∈R3,所以(10)式可写为:

由此得到空间R3中线性变换F的特征向量α的几何意义是:特征向量α是空间R3中点M的径矢量,即α=,而点M的坐标是(x1,x2,x3),属于特征根λ的所有特征向量aα都在由点(0,0,0)和点(x1,x2,x3)确定的直线OM上.因为F(α)与α的坐标成比例,所以矢量F(α)与矢量α线性相关.几何意义是:F(α)与α在过原点的直线OM上.
由(8)式~(10)式得,特征向量的充要条件是:设α=(x1,x2,x3)是非退化的线性变换F:R3→R3的属于特征根λ的一个特征向量,即


其中:ξ=αT是α的转置,它是三行一列矩阵,也是一个列向量,α=ξT;A=(aij)3×3是线性变换F的矩阵且是三阶单位方阵.因为特征向量ξ≠0,所以关于x1,x2,x3的三元一次齐次方程组(14)式有非零解x1,x2与x3的充要条件是它的系数行列式为零,即

(15)式称为线性变换F或三阶方阵A的特征方程.F的特征多项式是:

其中:I1=a11+a22+a33是矩阵A的迹;是矩阵A的行列式.由此可知,线性变换F的特征方程(15)式为:

这是关于λ的一元三次方程,设矩阵A是非对称矩阵.
下面讨论方程(17)式的根.
(1)设方程(17)式只有一个实数根λ1,将它代入方程组(14)式,可得一个特征向量α1=(X1,Y1,Z1),此时F(α1)=λ1α1.几何上,α1与F(α1)在经过原点的一条直线上,λ1对应的所有特征向量aα1=(aX1,aY1,aZ1)都在该条直线上,这就是特征根的几何意义.具体例子如下:

矩阵A的特征方程是:
解得矩阵A只有一个实的特征根λ1=1,再由(14)式得λ1=1对应的一个特征向量是α1=(3,1,-1),且F(α1)=α1λ.1=1对应的所有特征向量aα1=(3a,a,-a)在直线上,该直线上的点是线性变换F的不变点.
(2)设方程(17)式有三个实数根λ1,λ2,λ3且λ1≠λ2=λ3,将λ1代入方程组(14)式,可得对应的一个特征向量α1=(X1,Y1,Z1),则重根λ2=λ3对应的特征向量或只有一个α2=(X2,Y2,Z2),或有无穷多个.因为α1与α2的坐标不成比例(否则α2也是λ1对应的特征向量),所以α1与α2线性无关.几何上,α1与α2分别在经过原点的两条直线和上,这就是有一对重根对应的特征向量的几何意义.具体例子如下:

解得矩阵A的特征根λ1=2,λ2=λ3=1,再由(14)式得λ1=2对应的一个特征向量是α1=(1,1,-1),重根λ2=λ3=1对应的线性无关的特征向量只有一个α2=(1,0,0),α1与α2线性无关,且F(α1)=2α1,F(α2)=α2.几何意义是:λ1=2对应的所有特征向量都在直线上,λ2=λ3=1对应的所有特征向量都在x轴上,且α1与α2不同在一条直线上.

矩阵A的特征方程是:
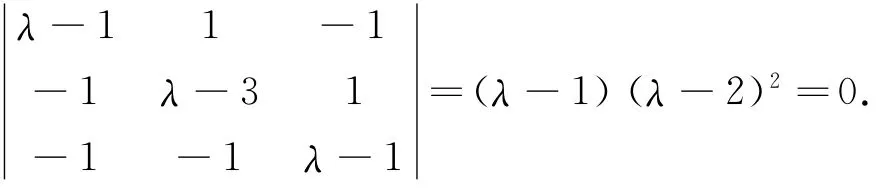
解得特征根λ1=1,λ2=λ3=2,λ1=1对应的一个特征向量是α1=(-1,1,1),重根λ2=λ3=2对应的特征向量是α=(X,Y,X+Y),其中X,Y是不全为零的任意实数,且F(α1)=α1,F(α2)=2α2.几何意义是:λ1=1对应的特征向量都在直线上,二重特征根λ2=λ3=2对应的特征向量都在直线上,且有无穷多个,即(X,Y,X+Y),且α1=(-1,1,1)与α=(X,Y,X+Y)不共线.
(3)设方程(17)式有三个互不相等的实数根λ1,λ2,λ3且λ1<λ2<λ3,将λ1,λ2,λ3分别代入方程组(14)式,可得三个特征向量α1=(X1,Y1,Z1),α2=(X2,Y2,Z2),α3=(X3,Y3,Z3),因为它们的坐标不成比例,所以它们两两线性无关.几何意义是:α1,α2和α3不共面,α1,α2和α3分别在经过原点的三条直线上.具体例子如下:

矩阵A的特征方程是:

解得特征根λ1=1,λ2=2,λ3=3,对应的特征向量分别是α1=(1,0,0),α2=(1,1,0),α3=(1,2,2),且F(α1)=α1,F(α2)=2α2,F(α3)=3α3.几何意义是:α1,α2和α3不共面,且分别在直线上.
(4)设方程(17)式有三个相等的非零实数根λ1=λ2=λ3≠0,对应的特征向量只有一个α1=X1,Y1,Z1().具体例子如下:
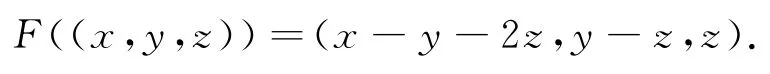
矩阵A的特征方程是:

解得特征根λ1=λ2=λ3=1,对应的特征向量只有一个α1=(1,0,0).几何意义是:λ1=λ2=λ3=1对应的所有特征向量都在直线上.
通过讨论,得如下空间中特征向量的几何意义的定理成立:
定理1 设F:R3→R3是空间R3中由三阶非对称实矩阵A=(aij)3×3对应的线性变换,即
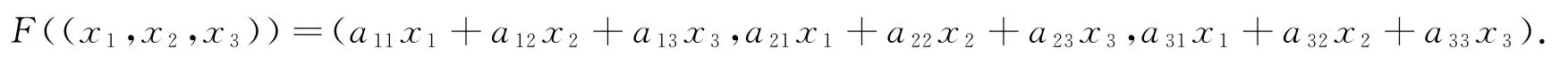
(1)设λ1是实数特征根,λ2,λ3是一对共轭的复数特征根,则线性变换F只有一个实的特征向量α1=(X1,Y1,Z1),此时F(α1)=λ1α1.几何上,α1与F(α1)在经过原点的一条直线上,λ1对应的所有特征向量aα1=(aX1,aY1,aZ1)都在该条直线上,这就是特征根的几何意义.
(2)设λ1,λ2,λ3是三个实数特征根且λ1≠λ2=λ3,λ1对应的一个特征向量是α1=(X1,Y1,Z1),则重根λ2=λ3对应的线性无关的特征向量或只有一个α2=(X2,Y2,Z2),或有无穷多个.几何上,α1与α2不共线,α1与α2分别在经过原点的两条直线和上,这就是有一对重根对应的特征向量的几何意义.
(3)设λ1,λ2,λ3是三个互不相等的实数特征根且λ1<λ2<λ3,λ1,λ2,λ3对应的三个特征向量分别是α1=(X1,Y1,Z1),α2=(X2,Y2,Z2),α3=(X3,Y3,Z3).几何意义是:α1,α2和α3不共面,α1,α2和α3分别在经过原点的三条直线上.
(4)设λ1,λ2,λ3是三个相等的非零实数特征根λ1=λ2=λ3≠0,则对应的线性无关的特征向量只有一个α1=(X1,Y1,Z1).所有的特征向量都在直线上.
2 空间R3 中对称矩阵对应的线性变换的特征向量的几何意义

矩阵A的特征方程是:

由文献[5]知,特征方程(19)式的根λ1,λ2,λ3都是实数,且不同的特征根对应的特征向量正交,即设λ1≠λ2对应的特征向量分别是α1=(X1,Y1,Z1),α2=(X2,Y2,Z2),则
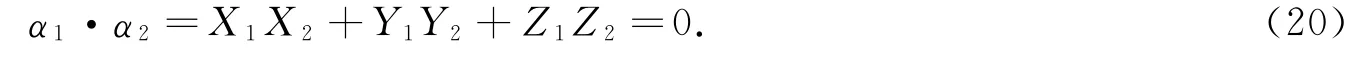
由文献[5]得,三阶实对称矩阵A有三重非零特征根λ1=λ2=λ3≠0的充要条件是:

此时线性变换是F((x,y,z))=(a11x,a11y,a11z)=a11(x,y,z),这是伸缩变换,对应的特征向量是自原点出发的任一非零矢量α=(X,Y,Z).
由此可得,三阶实对称矩阵A对应的线性变换的特征向量的几何意义的定理成立:
定理2 设F:R3→R3是空间R3中三阶实对称矩阵A=(aij)3×3对应的线性变换,即
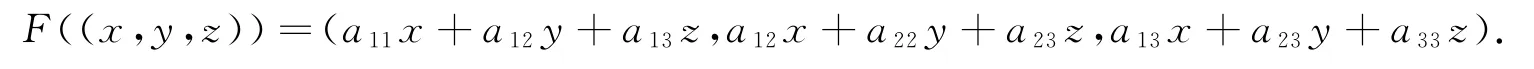
则它的特征根λ1,λ2,λ3都是实数.
(1)设三个特征根λ1,λ2,λ3两两不等,对应的三个特征向量分别是α1=(X1,Y1,Z1),α2=(X2,Y2,Z2),α3=(X3,Y3,Z3).特征根的几何意义是:它们两两垂直,即α1⊥α2,α2⊥α3,α3⊥α1.
(2)设λ1是单根,λ2=λ3是重根,λ1对应的一个特征向量是α1=(X1,Y1,Z1),则重根λ2=λ3对应的特征向量α=(X,Y,Z)满足

即平面X1x+Y1y+Z1z=0上自原点出发的任一非零矢量都是重根对应的特征向量,且单根对应的特征向量是该平面的法矢量.
(3)设三个特征根λ1,λ2,λ3相等,即λ1=λ2=λ3≠0,则自原点出发的任一非零矢量α=(X,Y,Z)都是重根对应的特征向量.
具体例子如下:
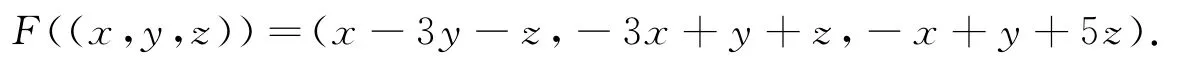
它的特征方程是:
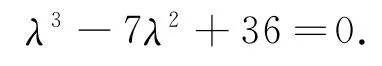
解得矩阵A 的特征根λ1=6,λ2=3,λ3=-2,对应的三个特征向量分别是α1=(-1,1,2),α2=(1,-1,1),α3=(1,1,0),显然特征向量两两垂直,这就是特征向量的几何意义,且F(α1)=6α1,F(α2)=3α2,F(α3)=-2α3,F(α1)与α1在直线上.因矩阵A的行列式,所以线性变换F是空间R3的一一变换.此时变换F是非退化的线性变换.
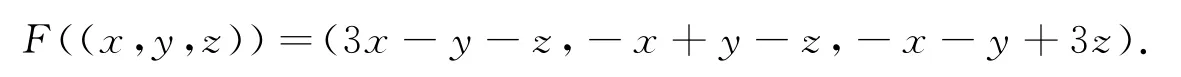
它的特征方程是:
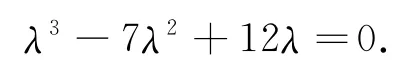
解得特征根λ1=4,λ2=3,λ3=0,对应的三个特征向量分别是:α1=(1,0,-1),α2=(1,-1,1),α3=(1,2,1),显然特征向量两两垂直,这就是特征向量的几何意义,且F(α1)=4α1,F(α2)=3α2,F(α3)=0.因为矩阵A的行列式,所以线性变换F是空间R3退化的线性变换,它将直线上的任一点(t,2t,t)映为原点(0,0,0),该直线外任一点的像是空间中的某一点,如F((1,2,3))=(-2,-2,3).
例2.1和例2.2给出了对称矩阵具有三个不同特征根对应的特征向量的几何意义.

因为矩阵A的行列式,所以线性变换F是空间R3的一一变换.它的特征方程是:

解得特征根λ1=2,λ2=λ3=-1,λ1=2对应的一个特征向量是α1=(1,1,1).重根λ2=λ3=-1对应的特征向量是α=(X,Y,Z)满足X+Y+Z=0,即重根λ2=λ3=-1对应的特征向量是α=(X,Y,-X-Y),其中X,Y是不全为零的任意实数.几何意义是:平面x+y+z=0上自原点出发的任意矢量都是重根λ2=λ3=-1对应的特征向量,该平面的法矢量=(1,1,1)就是单根λ1=2对应的特征向量,且F(α1)=2α1F(α)=-α.
例2.3给出了对称矩阵具有二重特征根对应的特征向量的几何意义.
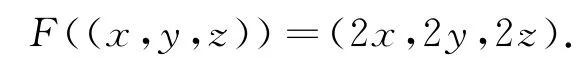
解得矩阵A的特征根是λ1=λ2=λ3=2,对应的特征向量是α=(X,Y,Z),其中X,Y,Z是不全为零的任意实数,α是空间R3中自原点出发的任意非零矢量.
例2.4给出了对称矩阵具有三重特征根对应的特征向量的几何意义.
[1]纪永强.微分几何(第2版)[M].北京:高等教育出版社,2012.
[2]北京大学数学系.高等代数(第2版)[M].北京:高等教育出版社,1988.
[3]张禾瑞,郝炳新.高等代数(第2版)[M].北京:人民教育出版社,1980.
[4]纪永强.平面上线性变换的特征向量的几何意义[J].湖州师范学院学报,2013,35(4):1-6.
[5]纪永强.空间解析几何(第1版)[M].北京:高等教育出版社,2013.
