平面上正交变换的特征向量的几何意义*

纪永强

(湖州师范学院理学院,浙江湖州 313000）

平面上正交变换的特征向量的几何意义*

纪永强

(湖州师范学院理学院,浙江湖州 313000）

利用代数方法给出了平面上正交变换的特征向量的几何意义,即研究了平面R2上的旋转变换(正交变换）,它无对应的实特征向量.同时研究了经过原点的直线的反射变换(正交变换）的特征向量就是该直线的法矢量和该直线的方向矢量,并且它们是互相垂直的.

特征向量;矩阵;正交变换

关于线性变换的特征向量的定义及有关性质,在文献[1]、[2]、[3]中都有讨论,文献[4]给出了平面上线性变换的特征向量的几何意义,现在我们研究平面上正交变换的特征向量的几何意义.本文给出它们的几何意义,这样对特征向量就有了直观的认识.其中：矩阵A=(aij）2×2是F关于标准正交基e1=(1,0）,e2=(1,0）的矩阵,矩阵A是正交矩阵：AAT= E2,其中E2是二阶单位方阵,AT是A的转置矩阵.

设F∶R2→R2是向量空间R2上的线性变换,e1=(1,0）和e2=(1,0）是R2的一组基(标准正交基）,设由参考文献[2]及[3],我们有特征向量的定义如下：

定义[2]设F∶R2→R2是向量空间R2上的线性变换,λ∈R,α是R2上的非零向量,若则称λ是线性变换F的一个特征根,α叫属于特征根λ的特征向量.

显然,对任a∈R,a≠0,有F(aα）=λ(aα）,所以aα是属于特征根λ的所有特征向量.因为α=(x1, x2）∈R2,所以(12）式可以写为：由此我们得到,平面R2上线性变换F的特征向量α的几何意义是：特征向量α是平面R2上点M的径矢量,即,而点M的坐标是(x1,x2）,属于特征根λ的所有特征向量aα都在由点(0,0）和点(x1,x2）确定的直线OM上.因为F(α）与α的坐标成比例,所以矢量F(α）与矢量α线性相关,几何上,F(α）与α在过原点的直线OM上.

由(10）式、(11）式和(12）式,我们得特征向量的充要条件如下：

设α=(x1,x2）是线性变换F∶R2→R2的属于特征根λ的一个特征向量,即

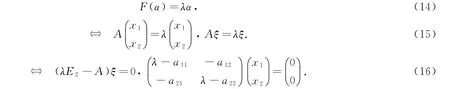
其中：ξ=αT是α的转置,它是二行一列矩阵,也是一个列向量,α=ξT.A=(aij）2×2是线性变换F的矩阵.因为特征向量ξ≠0,所以关于x1、x2的二元一次齐次方程组(16）式有非零解x1与x2的充要条件是：它的系数行列式为零,即

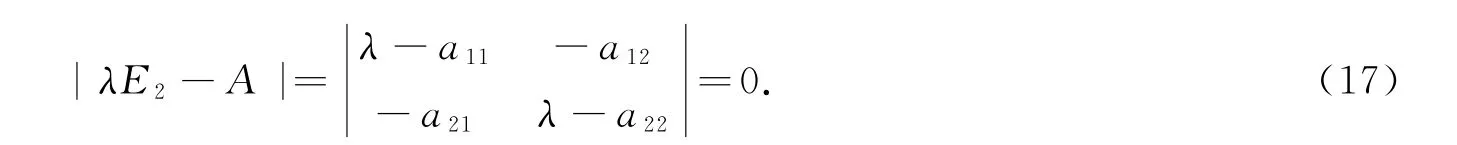
(17）式称为线性变换F或二阶方阵A的特征方程.

由文献[1]我们得,平面R2上的正交变换F只有两类：或者它是一个绕原点的旋转变换,此时对应的二阶矩阵A的行列式|A|=1;或者它是关于经过原点的直线的反射(对称）变换,此时对应的二阶矩阵A的行列式|A|=-1.由此我们得平面上正交变换的特征向量的几何意义的两个定理如下.

定理1设F∶R2→R2是平面R2上的旋转变换(正交变换）,即

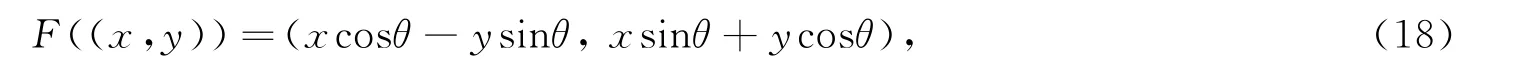
其中θ≠0,π.则旋转变换的特征方程无实根,从而无实的特征向量.证明上面的正交变换写成矩阵形式是：

因为AAT=E2,即矩阵A是正交矩阵,由(6）式知,旋转变换(18）式是正交变换,它是把平面R2上的点(x, y）绕原点逆时针旋转θ角的旋转变换.由(17）式,矩阵A的特征方程是：

因为方程(20）式的判别式Δ=4cos2θ-4=-4sin2θ＜0,所以旋转变换的特征方程无实数根,从而无实的特征向量.

具体例子如下：

定理2设F∶R2→R2是平面R2上的点(x,y）关于直线ax+by=0(a2+b2≠0）的反射(对称）变换,则F是正交变换,正交变换F的特征根是λ1=-1,λ2=1.λ1=-1对应的特征向量α1=(a,b）就是直线ax+by=0的法矢量,λ2=1对应的特征向量α2=(b,-a）就是直线ax+by=0的方向矢量,并且α1与α2垂直,直线ax+by=0上的任一点是正交变换的不变点.这就是平面R2上的正交变换的特征向量的几何意义.

证明设M1(x1,y1）是点M(x,y）关于直线ax+by=0的对称点,则点M1与点M的中点在该直线上,即

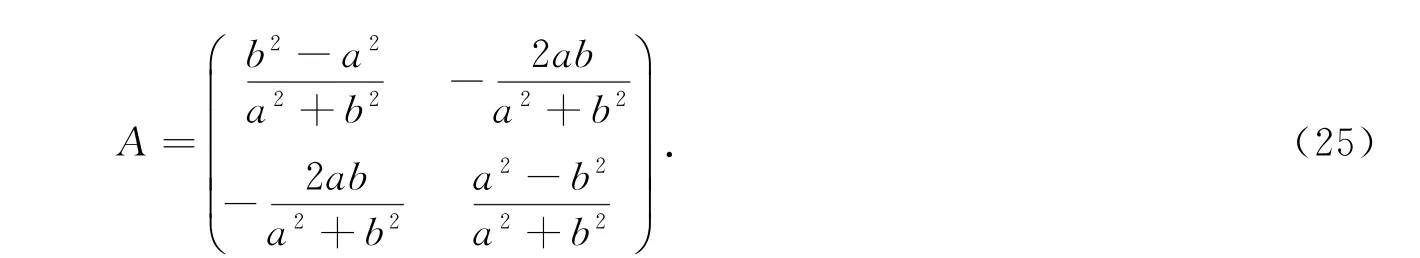
容易验证,AAT=E2,且|A|=-1,所以矩阵A是正交矩阵,由(6）式知,F是正交变换.矩阵A是二阶实对称矩阵,它的特征多项式是

α2就是直线ax+by=0的方向矢量.由(3）式,因为g(α1,α2）=ab-ab=0,即α1与α2的内积为零,所以两特征向量α1与α2正交,并且F(α1）=-α1,F(α2）=α2.几何上,α1与α2垂直,因为F(α2）=α2,所以直线ax+by=0上的点(b,-a）是正交变换F下的不变点.

具体例子如下：

令F((x,y））=(x,y）,得y=2x,所以正交变换(30）式是平面R2上的点(x,y）关于直线2x-y=0的反射变换,直线2x-y=0上的任意一点是该正交变换的不变点.由(17）式,矩阵A的特征方程是：

所以λ1=-1对应的一个特征向量是：

λ2=1对应的一个特征向量是：

α1就是直线2x-y=0的法矢量,α2是直线2x-y=0的方向矢量,α1与α2的几何意义是α1与α2垂直.

[1]纪永强.微分几何[M].北京：高等教育出版社,2012.

[2]北大数学系.高等代数[M].北京：高等教育出版社,1988.

[3]张禾瑞,郝炳新.高等代数高等代数[M].北京：人民教育出版社,1980.

[4]纪永强.平面上线性变换的特征向量是几何意义[J].湖州师范学院学报,2013,35(6）：1-6.

Geometric Meaning of the Feature Vector Orthogonal Transformation on the Plane

JI Yongqiang
(School of Science,Huzhou University,Huzhou 313000,China）

This paper presents the algebraic method of the geometric feature vector orthogonal transformation on the plane,i.e.the plane of rotation transformation,without the feature vectors corresponding to it,and studies the reflection transformation after the feature vector origin of the line is the straight-line method vector and the line direction vector,and they are perpendicular to each other.

feature vectors;matrices linear;orthogonal transformation

O186.11

A

1009-1734(2014）02-0001-05 MSC(2000）：53C17

2013-10-20

纪永强,教授,研究方向：微分几何.E-mail：jyq2008@hutc.zj.cn

MSC 2000：53C17