QR方法计算一般矩阵特征值和特征向量的算法研究

赵 洋 刘晓宙,2

(1.南京大学物理学院 江苏 南京 210093 2.近代声学教育部重点实验室，南京大学声学研究所 江苏 南京 210093)

引言

计算矩阵的特征值和特征向量是计算方法中一个常见的问题.一般常用的方法有乘幂法、反幂法，雅克比法和QR方法[1-2].乘幂法用于求矩阵的模最大的特征值和对应的特征向量[3]，反幂法用于求矩阵的模最小的特征值和对应的特征向量[4]，雅克比法计算实对称矩阵的特征值和特征向量[5].QR法通常仅用来求一般矩阵的特征值，获得特征值后采用反幂法来获得特征向量[6]，一般来说并不直接通过QR法获得特征向量.但是反幂法存在着其缺陷，它对输入的试探向量的值有一定要求，在只进行一次尝试的情况下得到的不一定就是想要的特征向量[7][8],需要对幂法做一些改进和补充才能得到想要的结果[9].为了避免迭代法中初值的影响，本文探索直接采用QR算法获得特征值和特征向量的方法，讨论了用QR方法在不同情况下特征向量的一些算法，并对算法进行了验证.

1 QR方法计算特征值和特征向量的一般方法

1.1 QR分解

QR分解的基本步骤是：令A0=A,对k=1,2,…

分解Ak-1=Qk-1Rk-1

(1)

其中Qk-1为正交矩阵，Rk-1为上三角矩阵.

令Ak=Rk-1Qk-1

(2)

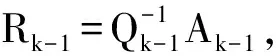
(3)

从而Ak～Ak-1～…～A0

(4)

假设对于矩阵Ak，有特征值λk,特征向量Xk，

即 AkXk=λkXk

(5)

代入(3)式，得：

(6)

即有：

Ak-1(Qk-1Xk)=λk(Qk-1Xk)

(7)

由(4)式可知，Ak-1和Ak具有相同特征值λk.Ak-1的特征向量为Xk-1=Qk-1Xk,

递推可得：Ai(i=1,2,…,k)具有相同特征值λk，A0的特征向量为X0=Q0Q1…Qk-2Qk-1Xk.

因此，如果Ak的特征值和特征向量有办法求出，那么就能获得A0的特征值和特征向量.下面分别对特征值和特征向量两部分的求解做介绍.

1.2 矩阵特征值的导出

先介绍几个定理[9]：

定理1 设A=(aij)∈Rn×n

1°如果A的特征值满足：|λ1|>|λ2|>…>|λn|>0

2° A有标准型A=XDX-1其中D=diag(λ1,λ2,…,λn)，且设X-1有三角分解X-1=LU(L为单位下三角阵，U为上三角阵)，则由QR算法产生的{Ak}本质上收敛于上三角阵.

定理2 设A=(aij)∈Rn×n，如果A的等模特征值中只有实重特征值或者多重复的共轭特征值，则QR算法产生的{Ak}本质收敛于分块上三角阵(对角块为一阶和二阶子块)且对角块每一个2×2子块给出A的一对共轭复特征值，每一个对角子块给出A的实特征值.

本文讨论的矩阵均满足上述定理，可以通过QR算法收敛于分块上三角阵，求得特征值.

1.3 矩阵特征向量的导出

在不借助幂法的情况下，采用直接由特征值特征向量的定义计算.

特征值特征向量的定义为：存在某个向量ξ，使得Aξ=λξ，那么就称λ为矩阵的一个特征值，ξ为其对应的特征向量.所以在特征值已知的情况下，只要求解：

(A-λE)ξ=θ

(8)

即可求出特征值λ对应的特征向量ξ，即求新矩阵A-λE的零空间.

下面说明零空间的求法：

任意一个矩阵均可以通过行变换化为行最简形矩阵.行最简形矩阵的定义为非零行的第一个非零元素全是1，且非零行的第一个元素1所在列的其余元素全为零.例如：

(9)

接下来就将借助行最简形矩阵求出矩阵的零空间.

对于一个矩阵A和它的行最简形矩阵U，Ax=θ和Ux=θ应当为同解方程组，求出U的零空间就求出了A的零空间.

对U做适当的列交换，可以把U化成如下U'的形式

(10)

I是单位矩阵，K是一个一般的非零矩阵.

由于列交换会将解x中的变量顺序交换，所以求出U′x′=θ的解x'后，将其中的变量依照列变换顺序反变换回去，就得到了我们想要的解x.

2 不同类型矩阵特征值和特征向量的具体计算

前文已经得到了特征值和特征向量求解的主要算法.下面对不同情况的矩阵进行进一步的讨论，主要分类为实对称矩阵和一般实系数矩阵.在一般实系数矩阵的讨论中又分为可对角化矩阵和不可完成对角化的矩阵.

2.1 实对称矩阵

当A0为实对称阵时，特征值均为实数，且经过正交相似变换后得到的仍然是一个实对称阵，所以经过QR算法最终一定收敛到一个对角阵A∞.

(11)

很容易知道单位阵I中任意一个列向量均能成为该对角阵的特征向量，所以可以认为它的特征值组成的矩阵就是单位阵I.由此A0的特征向量组成的矩阵可表示为:

Q0Q1……Qk-2Qk-1I=Q0Q1…Qk-2Qk-1=P

(12)

取P的列向量即得到A的特征向量.

2.2 一般实系数矩阵

对于非实对称的矩阵，它和实对称矩阵主要有如下区别：

(1)矩阵不一定可以对角化.即在特征值出现重根的情况下，n阶方阵不一定有n个线性无关的特征向量.

(2)特征值不一定都是实数.所以经过QR法计算出来最终收敛的矩阵可能是一个分块上三角阵，此时的特征值会出现共轭复根.

(3)(拟)上三角化后得到的矩阵A∞的特征向量不再具有单位阵这样的简单形式，需要通过求矩阵零空间的方法将特征向量求出.

所以对一般实系数矩阵求特征值的步骤为：使用QR法让其收敛到一个(分块)上三角阵，将正交相似变换矩阵Q存下来，求出该(分块)上三角阵的特征值和特征向量，求出的特征值就是对应原矩阵的特征值，特征向量经过矩阵Q的作用得到原矩阵的特征向量.

由于零空间的算法具有普适性，所以不论矩阵是否可以对角化，总能求出所有线性无关的解，可以根据最终求得的特征向量的个数来判断是否可以对角化.

3 计算实例

3.1 实对称阵

先选取了一个特征值均为单重根的实对称矩阵的情况：

各符号代表的含义是：λ0为matlab内置函数计算出来的特征值，λ为QR算法求出来的上三角阵的对角线元素，Q为算法中的正交矩阵不断累乘得到的变换矩阵，在此情况下，Q的每一列就对应着A的一个特征向量.后续经过特征向量的定义验证该结果正确.

选取特征值含重根的实对称矩阵验证，计算结果也是正确的.

3.2 一般实系数的特征值和特征向量

特征值均为单根且可以对角化的例子：

其中A为待求矩阵，λ0为matlab内置函数求出的特征值，λ为QR方法计算后的分块上三角阵的特征值.P是分块上三角阵的线性无关的特征向量，D为正交相似变换矩阵，P1=DP就是A的特征向量.

考虑特征值出现重根且矩阵不可对角化的例子：

符号含义与上例相同，和上例的区别在于求出来的P只有三个线性无关的列向量，矩阵无法完成对角化.使用matlab内置函数验证时，特征向量有两列是线性相关的，这也验证了该矩阵无法完成对角化.

4 结论

采用QR方法计算一般实系数矩阵的特征值和特征向量，此方法的优点在于不需要输入试探向量进行迭代，避免了幂法中最终结果的正确性与输入的试探向量直接相关的问题.而且该算法具有普适性，不论矩阵是否可以对角化，只要能够满足定理条件，用QR算法最终收敛到一个(拟)上三角阵，就可以求得所有的特征值和对应的特征向量.利用该(拟)上三角阵求解零空间时比较方便，因为拟三角阵近似一个行梯形，在变成行最简型矩阵时更为方便.整个算法的缺点是需要在QR分解的时候将每次的正交相似变换阵Q累乘起来，加大了一定的计算量.