考虑几何偏差及重力影响的单层网壳冲击相似律研究

钟渝楷， 姜正荣， 姚小虎， 石开荣， 罗 斌

(1. 华南理工大学 建筑设计研究院， 广州 510640; 2. 华南理工大学 土木与交通学院， 广州 510640;3. 华南理工大学 亚热带建筑科学国家重点实验室， 广州 510640; 4. 东南大学 土木工程学院， 南京 211189)

网壳结构造型优美，轻巧且刚度大，目前被广泛应用于体育场馆等大型公共建筑，由于覆盖空间大，可容纳几千人甚至上万人，故其安全性极其重要。一旦发生恐怖袭击或意外爆炸冲击等，会造成巨大的人员财产损失和社会恐慌。因此，对该结构的冲击动态响应研究十分必要。

目前，国内研究已取得较大进展。郭可[1]率先对K8型单层网壳在顶点冲击载荷下的动力响应进行试验研究。王多智等[2-4]利用数值模拟对K8型单层网壳进行了较全面的参数研究，并用试验验证了有限元模型的可靠性。王秀丽等对带下部支承结构的K6型单层网壳进行模型试验和数值模拟，得到响应规律和参数影响关系[5-7]；同时研究单层网壳临界冲击动能，获得拟合公式[8]。丁北斗等[9]通过试验研究单层网壳动态响应及失稳。然而，上述模型试验主要集中于数值方法的验证，并未涉及相似律的研究。由于工艺的限制或避免材料特性发生变化，工厂制作小模型构件时往往会出现几何偏差；实际试验时，模型和原型均受重力作用，其影响不可忽略，故对计及几何偏差和重力影响的相似律研究具有重要意义。

本文对凯威特-联方型混合网格单层网壳在顶点受冲击物冲击的相似律进行研究，考虑材料应变率效应、几何偏差和重力影响等因素，推导原型与模型的相似关系。采用非线性有限元软件LS-DYNA建立与已有文献相同的模型，验证数值方法的可靠性。此外，进行两例算例分析，在考虑应变率效应的基础上，分别考虑几何偏差和同时考虑几何偏差及重力影响，验证相似律分析结果的正确性及可操作性。

1 网壳冲击相似律

若模型和原型冲击姿态和边界条件相同，且同时忽略碰撞过程中的热效应，则网壳顶点受冲击物冲击时的位移w可表示为

w=f(aq,aq1,…,aqn,ρq,Eq,νq,Yq;D,t,l,δ,ρ,E,ν,Y;vq)

(1)

式中：aq,aq1,…,aqn为冲击物尺寸；ρq、Eq、νq和Yq分别为冲击物质量密度、弹性模量、泊松比和动态屈服强度；D和t分别为网壳钢管直径、壁厚；l和δ分别为网壳跨度和矢高；ρ、E、ν和Y分别为网壳杆件质量密度、弹性模量、泊松比和动态屈服强度；vq为冲击物速度。

以冲击物质量密度ρq、网壳跨度l和动态屈服强度Y为基本物理量，式(1)可化为无量纲函数关系

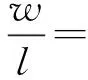
(2)

考虑模型和原型几何相似且均采用钢材，忽略弹性模量变化，式(2)可简化为

(3)

与模型和原型相关的物理量分别用下标m和p表示，βK=Km/Kp表示模型和原型相关物理量的比值。令Π=vq/(Y/ρq)1/2，若模型和原型满足相似关系，需Πm=Πp，得

(4)

材料在冲击下需考虑应变率效应，可用Cowper-Symonds模型表示[10]

(5)

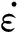
将式(5)代入式(4)，得

(6)

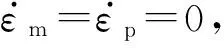
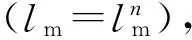
(7a)

(7b)

由于模型和原型均采用钢材，故ρ和Ys相同，将式(7a)和式(7a)代入式(6)，得

(8)

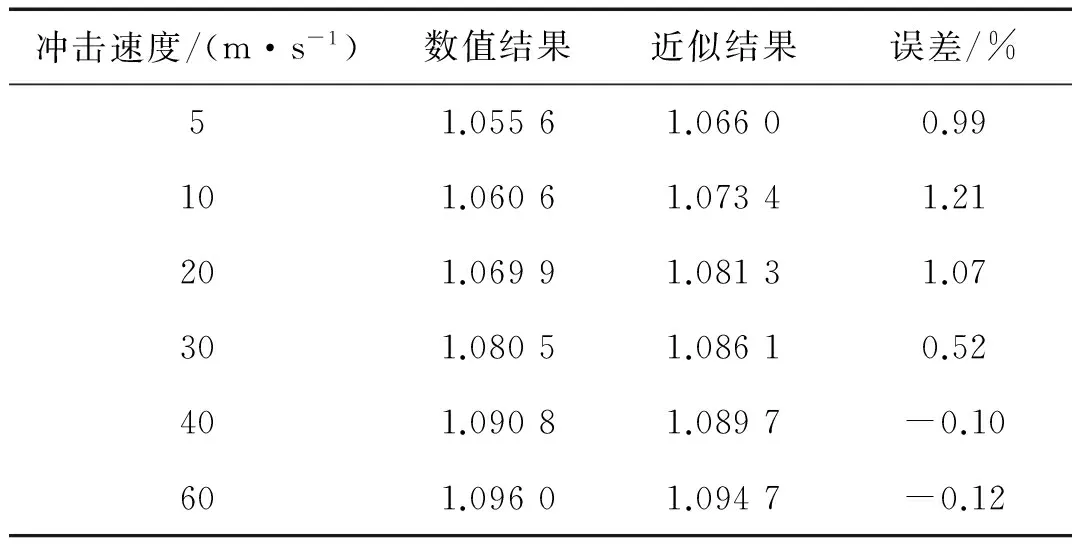
表1为下文分析模型(几何比1∶10，跨度6 m、矢高1 m的凯威特-联方型单层网壳)在不同冲击速度下βvq的值，其中数值结果由数值模拟得到的应变率代入式(8)所得，近似结果由冲击速度和结构特征长度的比值得到的应变率代入式(8)所得。可以看到，两者极为相近，说明后者是可靠的。因为近似结果可通过计算直接得到，不需通过试验或数值模拟，故下文分析采用近似结果。

1.1 考虑几何偏差影响的相似关系

模型(特别是小比例模型)的构件尺寸往往很小，由于制作工艺及条件限制，工厂生产的模型构件往往某个方向的尺寸被整体缩放，从而出现几何偏差，或为避免制作过程导致材料特性发生变化，特意放大模型尺寸。图1所示，几何比1/2的模型中，杆件的壁厚并未遵循1/2缩小，出现几何偏差。

表1βvq数值模拟与近似结果对比

Tab.1Comparisonofβvqbetweennumericalsimulationandapproximateresults

冲击速度/(m·s-1)数值结果近似结果误差/%51.05561.06600.99101.06061.07341.21201.06991.08131.07301.08051.08610.52401.09081.0897-0.10601.09601.0947-0.12

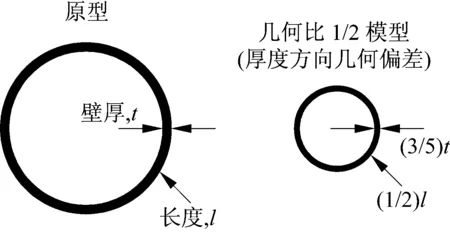
图1 杆件壁厚偏差

文献[14]引入f2=f(βX/βl)=(βX/βl)nv来考虑几何偏差的影响，其中βX=Xm/Xp为模型出现几何偏差部位与原型的几何之比，nv为指数，通过计算得到。由此，考虑几何偏差的速度比

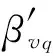
(9)

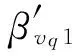
1.2 考虑重力影响的相似关系

在冲击荷载作用下，网壳的重力影响不能忽略，式(3)添加高度项和重力项

(10)

式中：h为冲击物所处高度，g为重力加速度，其他参数与前文一致。令Π1=h/l，Π2=gρql/Y。

由于原型与模型重力场一致，即βg=1。

由(Π2)m=(Π2)p，得

βY=βlβρq

(11)

将式(11)代入式(4)，得速度比

(12)

由式(11)得质量密度比

(13)

由式(13)可知，由于βl≠1且βY≠1，且一般βl≠βY，故βρq≠1，这表明要满足相似关系，需原型与模型质量密度不同。为方便起见，模型仍采用与原型相同的材料(如钢材)，通过配重来变相满足质量密度比的要求，网壳通过添加节点质量，冲击物通过增大高度方向尺寸实现配重，从而满足相似关系[15]。

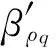
(14)

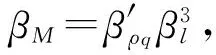
(15)

式中：Mp为原型的质量；Mm为模型的质量。

2 数值模拟验证

2.1 有限元模型的验证与分析模型的建立

对郭可的网壳冲击试验进行数值模拟对比验证。试验模型为K8型单层网壳，跨度1 202 mm，矢高248.7 mm，曲率半径850 mm，划分为4频；杆件采用直径4 mm的钢丝，节点取20 mm钢球，冲击物为0.35 kg长方体落锤，尺寸0.1 m×0.1 m×0.02 m，受重力作用自由落体冲击网壳顶点，下落高度分别为1 m和1.5 m，如图2所示。

采用LS-DYNA建立有限元模型。杆件采用BEAM161单元，每根杆件划分为3个单元，本构关系采用分段线性塑性模型“MAT_PIECEWISE_ LINEAR_PLASTICITY”，质量密度ρ=7 850 kg/m3，泊松比ν=0.3，弹性模量E=206 GPa，屈服强度235 MPa，失效应变0.25，强化系数a=40 s-1，b=5。冲击物采用SOLID165单元，本构关系采用刚体“MAT_RIGID”，材料基本参数与杆件一致。球节点采用质量单元MASS166施加在各节点，整个模型施加重力加速度场，方向竖直向下。冲击物与网壳接触采用点面接触(NODE-TO-SURFACE)。

试验中测量7根杆件轴力(见图3)、冲击接触力峰值和接触时间。数值模拟值和试验值的对比分别如表2～表4所示。

(a)俯视图(b)侧视图

图2 试验模型

Fig.2 Experimental model

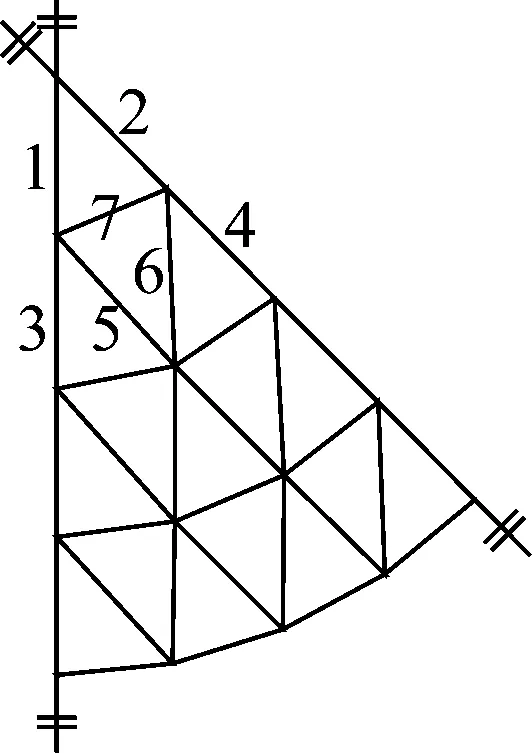
图3 测量杆件

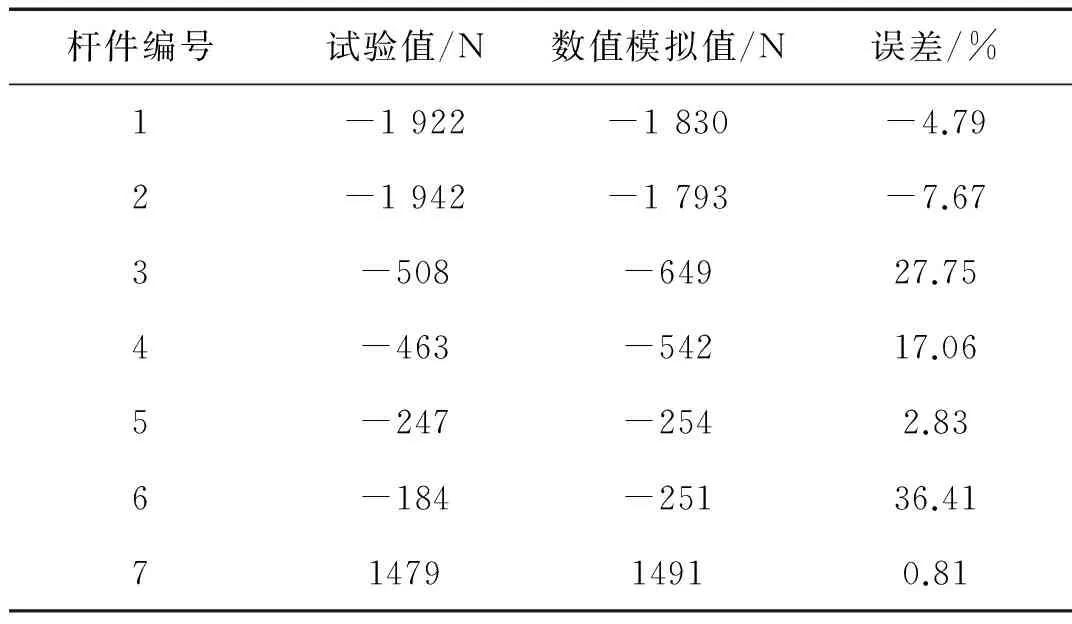
杆件编号试验值/N数值模拟值/N误差/%1-1922-1830-4.792-1942-1793-7.673-508-64927.754-463-54217.065-247-2542.836-184-25136.417147914910.81

由表2、表3可见，除个别数据误差较大，杆件轴力峰值的模拟值与试验值均吻合较好，最小误差仅为0.81%；轴力分布规律基本一致，主肋和环杆轴力较大，斜杆轴力较小，主肋和斜杆主要受压力，环杆主要受拉力，且对称杆件的轴力对称性均较好。由表4可知，冲击持时非常短暂，试验值与模拟值均在3～4 ms，而接触力峰值同样较为接近。由此说明，有限元分析结果是可靠的。

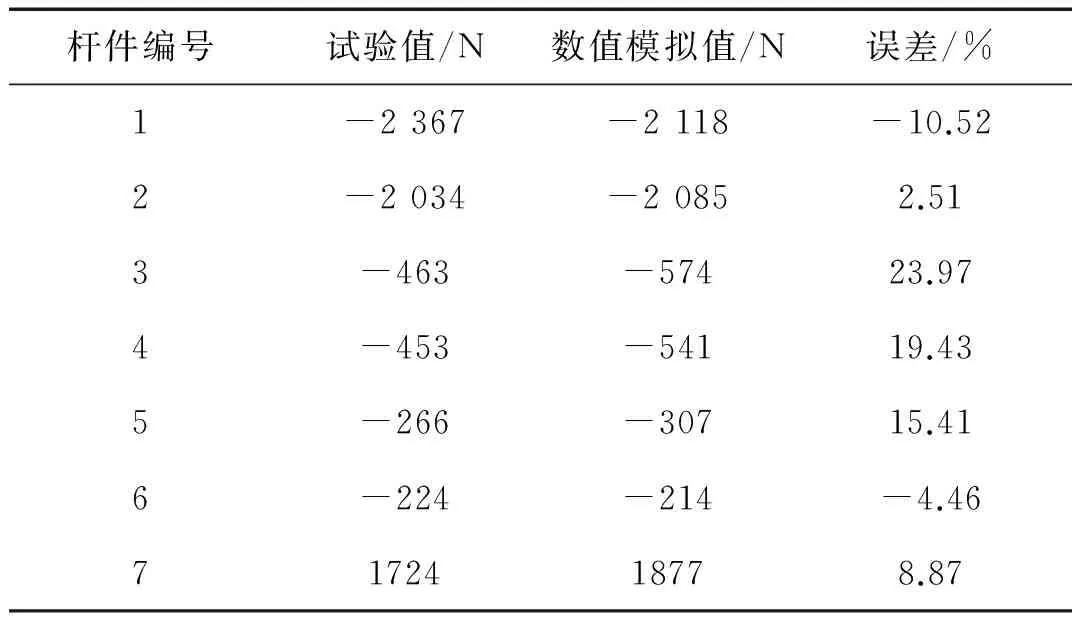
表3 杆件轴力数值模拟值和试验值对比(1.5 m)

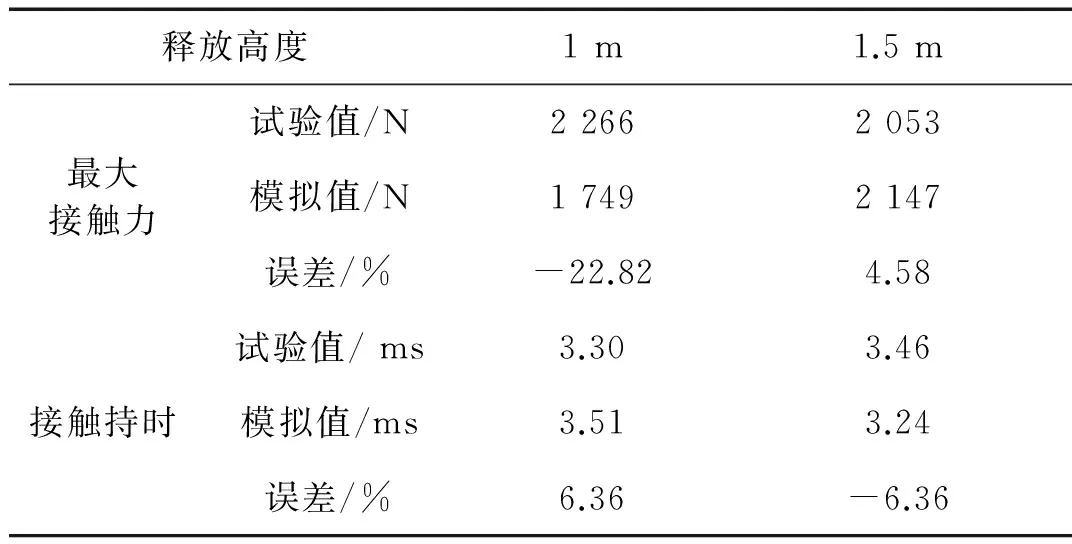
表4 接触力及接触持时数值模拟值和试验值对比

对比郭可试验的数值结果，本文的模拟精度相比更高。主要原因可能是因为郭可未计及材料的应变率效应、接触算法选择的差异和软件版本升级等对精度提高的影响。数值模拟值与试验值产生误差的原因可能是：有限元模型并未考虑冲击过程中材料热能、摩擦等消耗，且忽略节点刚度的贡献；试验时杆件及节点有累积损伤，冲击时难以正对节点冲击等。

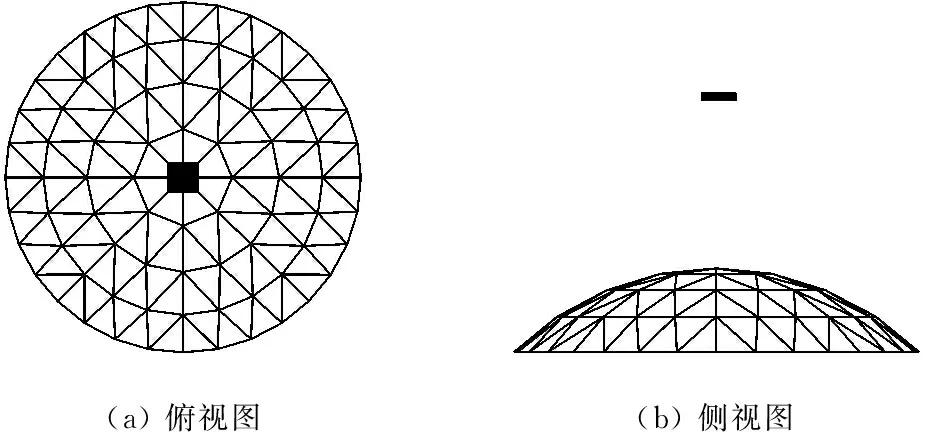
图4所示，利用LS-DYNA软件建立跨度60 m、矢跨比1/6的凯威特-联方型单层球面网壳作为原型。外围两环为联方型网格，其他为凯威特型网格。凯威特型网格的主肋和环杆采用φ180×8，斜杆采用φ168×6；联方型环杆为φ168×5.5，斜杆为φ180×7，均为圆钢管。冲击物采用直径为3 m，高度为1 m的圆柱体。为了模拟实际材料性能，将刚体模型改为分段线性塑性模型，其他材料参数和接触设置与上述试验验证模型一致。按原型建立几何比βl=1/10的模型。

(a)俯视图(b)侧视图

图4 凯威特-联方型单层网壳模型

Fig.4 Model of Kiewitt-Lamella single layer reticulated shell

2.2 考虑几何偏差影响的数值验证

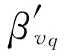
表5 速度10 m/s时nv确定过程

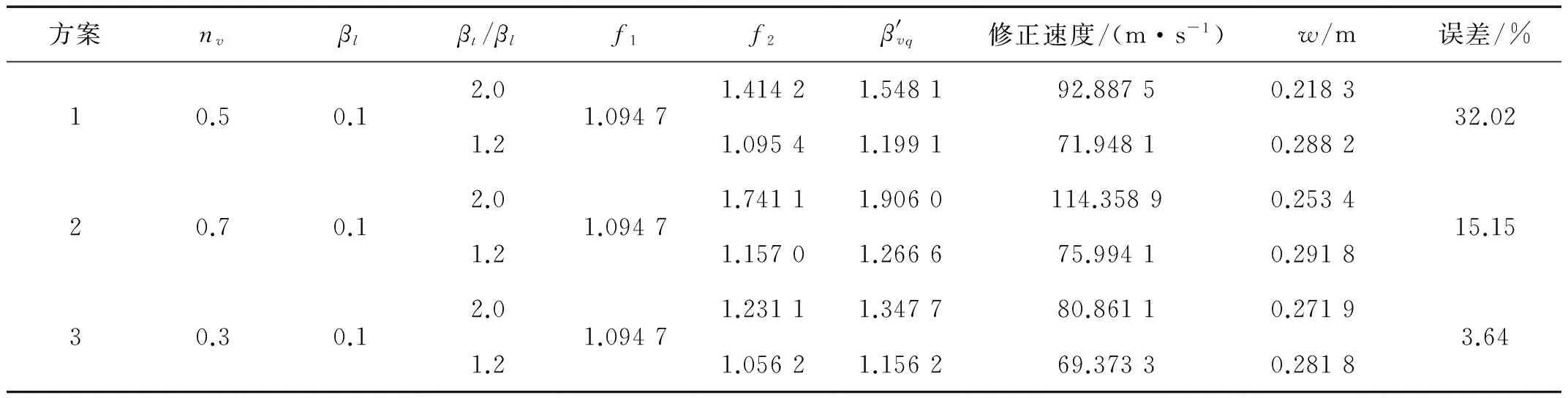
表6 速度60 m/s时nv确定过程

由表5可知，冲击物速度为10 m/s、nv=0.5时，两个模型竖向位移误差仅为2.51%，满足工程精度要求，故nv一步就得到。表6给出60 m/s时nv的确定过程，nv=0.5时误差为32.02%，大于25%，步长改为0.2，第三步时nv=0.3，误差为3.64%，同样满足工程精度要求。故速度为10 m/s和60 m/s时，nv分别取0.5和0.3。

表7所示，未修正模型表示相似关系未考虑应变率和几何偏差的影响，速度与原型一致；修正模型表示考虑应变率和几何偏差的影响，模型竖向位移w为按比例放大后得到的。表中可见，对不同几何偏差量，修正模型均能较好地预测原型位移，其误差均小于4%，而未修正模型预测原型结果误差均较大，甚至达到684.75%。

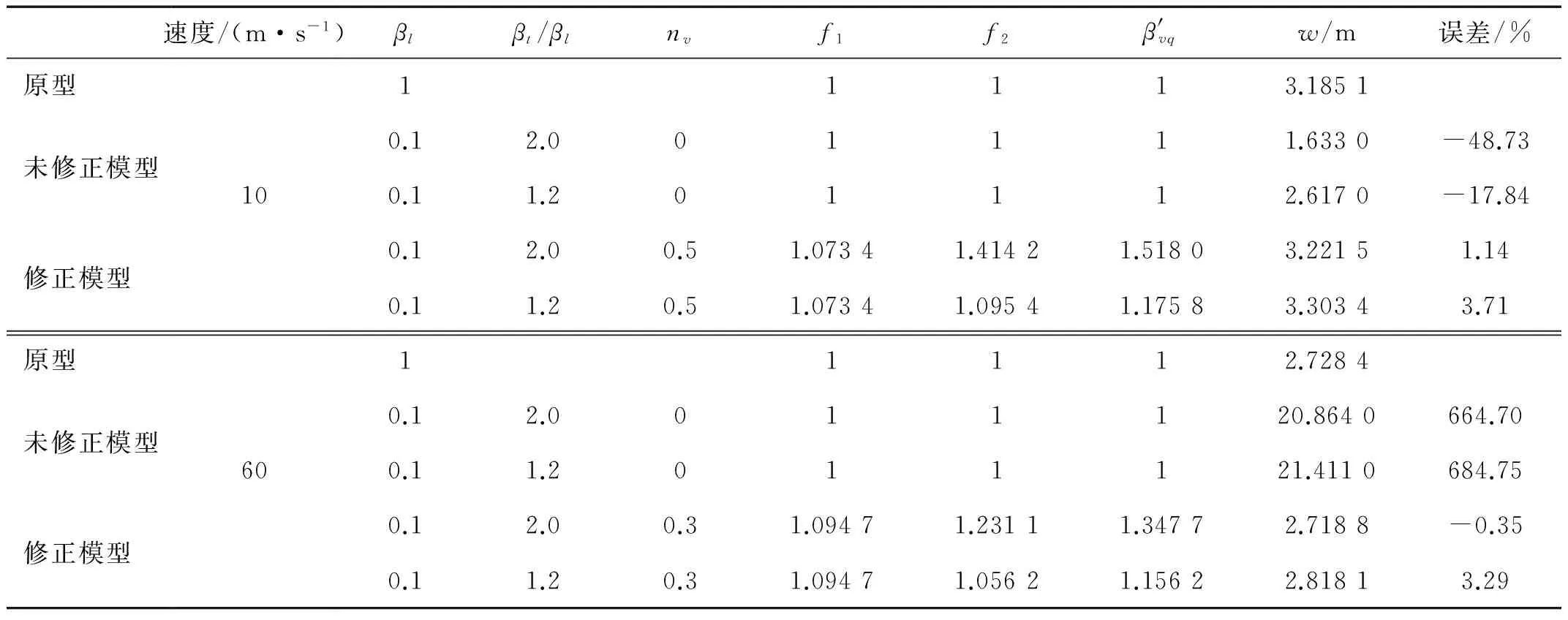
表7 模型预测结果与原型对比

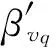
2.3 同时考虑几何偏差和重力影响的数值验证

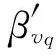
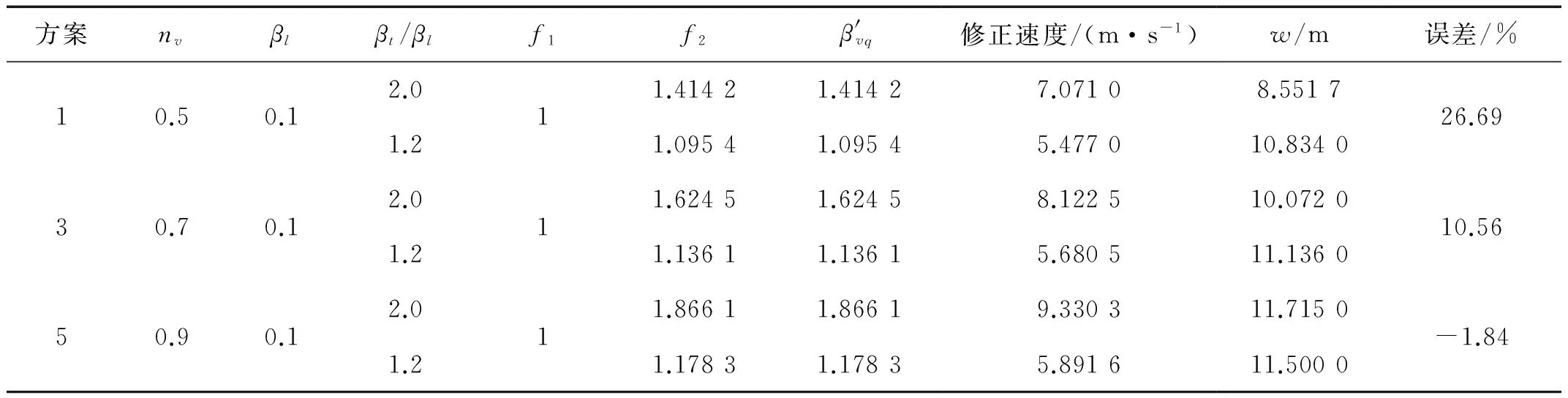
表8 速度5 m/s时nv确定过程

表9 速度40 m/s时nv确定过程

由表8和表9可知，分别经过三步和两步便收敛得到nv，nv分别为0.9和0.6。

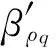
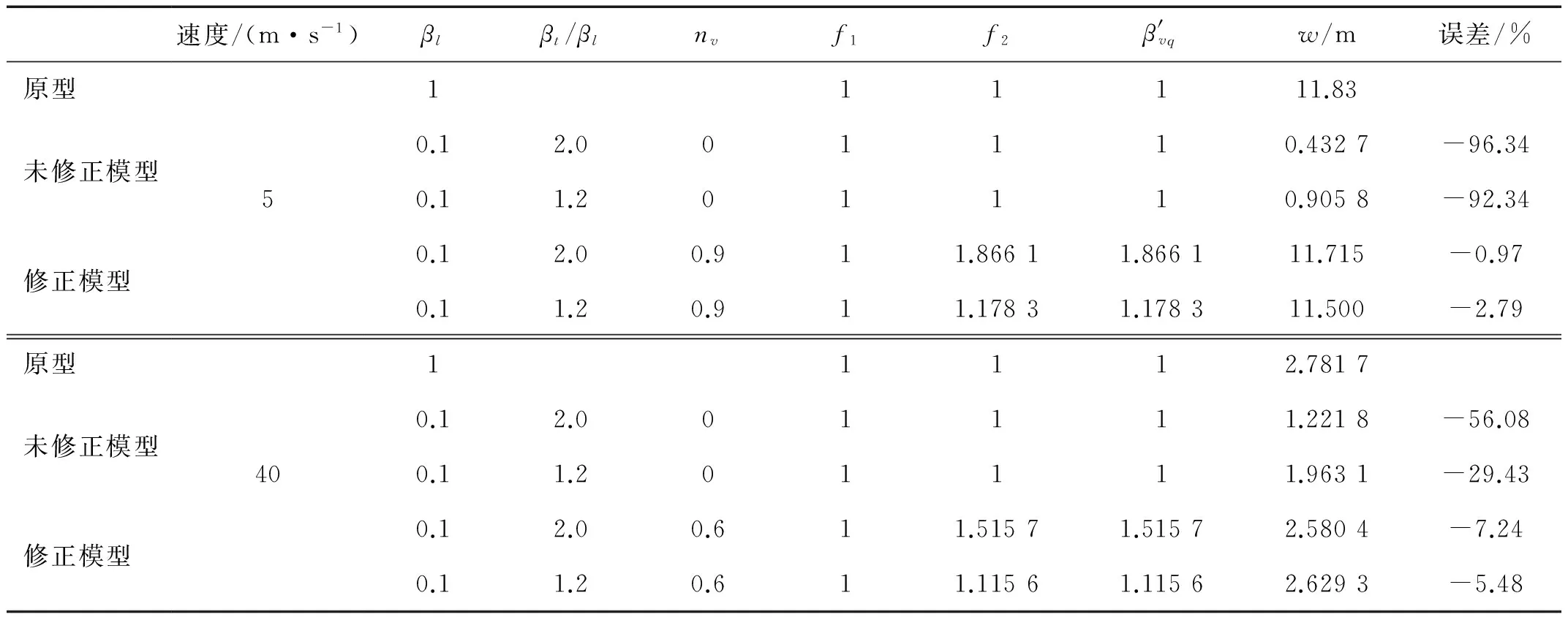
表10 模型预测结果与原型对比

3 结 论

根据量纲分析，在考虑应变率效应的基础上，分别考虑几何偏差和重力的影响，对单层网壳顶点受冲击物冲击的相似律进行了推导，给出了模型和原型动态响应的相似条件。利用已有文献的试验模型进行数值模拟，验证有限元分析方法的可靠性。在此基础上，建立分析模型，分别考虑几何偏差和同时考虑几何偏差及重力的影响，并将计算结果与未修正模型进行对比。研究表明：无论是考虑几何偏差或同时考虑几何偏差及重力的影响，本文给出的相似关系均能较好地预测原型的动态响应，而未修正模型预测结果与原型误差很大，不能用于工程实践。鉴于此，对类似结构的冲击响应研究，建议考虑上述因素的影响。

[1] 郭可. 单层球面网壳在冲击载荷作用下的动力响应分析[D]. 太原: 太原理工大学, 2004.

[2] FAN Feng, WANG Duozhi, ZHI Xudong, et al. Failure modes of reticulated domes subjected to impact and the judgment[J]. Thin-Walled Structures, 2010, 48(2): 143-149.

[3] 王多智. 冲击荷载下网壳结构的失效机理研究[D]. 哈尔滨: 哈尔滨工业大学, 2010.

[4] 王多智, 范峰, 支旭东, 等.冲击荷载下网壳结构的失效模式及其动力响应特性[J]. 工程力学, 2014, 31(5): 180-189.

WANG Duozhi, FAN Feng, ZHI Xudong, et al. Failure modes and characteristics of dynamic response for reticulated shells under impact[J]. Engineering Mechanics, 2014, 31(5): 180-189.

[5] 王秀丽, 马肖彤, 吴长, 等. 钢管柱支承单层网壳结构抗冲击动力性能试验研究[J]. 振动工程学报, 2015, 28(5): 683-691.

WANG Xiuli, MA Xiaotong, WU Chang, et al. Shock resistance dynamic performance tests on single-layer dome supported with steel tube column[J]. Journal of Vibration Engineering, 2015, 28(5): 683-691.

[6] 吴长, 王秀丽, 马肖彤, 等. 冲击荷载下单层球面网壳动力响应分析与试验研究[J]. 振动与冲击, 2014, 33(22): 88-96.

WU Chang, WANG Xiuli, MA Xiaotong, et al. Numerical analysis and experimental study on the dynamic response of single-layer reticulated shell under impact[J]. Journal of Vibration and Shock, 2014, 33(22): 88-96.

[7] 马肖彤, 王秀丽, 冉永红, 等. 带下部支承柱单层球面网壳结构抗冲击动力性能研究[J]. 振动与冲击, 2015, 34(24): 170-176.

MA Xiaotong, WANG Xiuli, RAN Yonghong, et al. Shock resistance performance of single-layer spherical reticulated dome with lower supporting column[J]. Journal of Vibration and Shock, 2015, 34(24): 170-176.

[8] 王秀丽, 王昊, 施刚, 等. 单层网壳结构冲击响应模式及临界冲击动能研究[J]. 工程力学, 2015, 32(7): 81-87.

WANG Xiuli, WANG Hao, SHI Gang, et al. Study on impact response modes and critical impact kinetic energy of single-layer reticulated shell[J]. Engineering Mechanics, 2015, 32(7): 81-87.

[9] 丁北斗, 吕恒林, 李贤, 等. 单层柱面网壳冲击试验研究[J]. 振动工程学报, 2015, 28(5): 692-702.

DING Beidou, LÜ Henglin, LI Xian, et al. Experimental study on single-layer cylindrical reticulated shell under impact force[J]. Journal of Vibration Engineering, 2015, 28(5): 692-702.

[10] COWPER G R, SYMONDS P S. Strain hardening and strain-rate effects in the impact loading of cantilever beams[R]. Brown University, Technical Report No. 28, 1957.

[11] 余同希, 卢国兴. 材料与结构的能量吸收[M]. 北京: 化学工业出版社, 2005: 56-58.

[13] 秦健, 张振华. 原型和模型不同材料时加筋板冲击动态响应的相似预报方法[J]. 爆炸与冲击, 2010, 30(5): 511-516.

QIN Jian, ZHANG Zhenhua. A scaling method for predicting dynamic responses of stiffened plates made of materials different from experimental models[J]. Explosion and Shock Waves, 2010, 30(5): 511-516.

[14] OSHIRO R E, ALVES M. Predicting the behaviour of structures under impact loads using geometrically distorted scaled models[J]. Journal of the Mechanics and Physics of Solids, 2012, 60(7): 1330-1349.

[15] 迟世春, 林少书. 结构动力模型试验相似理论及其验证[J]. 世界地震工程, 2004, 20(4): 11-20.

CHI Shichun, LIN Shaoshu. Validation of similitude laws for dynamic structural model test[J]. World Earthquake Engineering, 2004, 20(4): 11-20.

[16] 王多智, 范峰, 支旭东, 等. 考虑重力效应的单层球面网壳抗冲击荷载性能[J]. 哈尔滨工业大学学报, 2009, 41(8): 19-23.

WANG Duozhi, FAN Feng, ZHI Xudong, et al. Performance of single-layer reticulated domes under impact load and gravity[J]. Journal of Harbin Institute of Technology, 2009, 41(8): 19-23.