弹簧和密封圈刚度和阻尼对气体端面密封追随性的影响研究

张树强， 王 良， 陈 杰， 赵伟刚

(西安航天动力研究所，西安 710100)

气体端面密封以其不可替代的优势在高速旋转的设备中被广泛采用，稳健的密封气膜是其正常工作的重要保证。理想情况下密封动、静环端面均垂直于转轴，密封气膜稳定，然而在实际工作中，由于制造误差、装配误差等、热变形、力变形以及转轴振动等原因，密封气膜是随时间动态变化的。如若补偿环(一般为静环)不能对非补偿环(一般为动环)的振动提供良好的动态跟踪响应(称为追随性)，密封端面间的气膜将会发生失稳，出现密封泄漏量增大或者端面接触摩擦的现象，最终导致密封失效。

诸多学者对气体端面密封的动态特性进行了深入研究。国内，张树强等[1]基于摄动法研究了动静压混合式气体端面密封追随性；宋鹏云等[2]研究了实际气体效应对T形槽干气密封动态刚度和阻尼系数的影响规律；刘向锋等[3]等基于半解析法研究了极端工况下干气密封动态特性；丁雪兴等[4]研究了热耗散变形下干气密封系统的轴向振动稳定性。国外，Green等[5]研究了不同转轴速度和密封环锥角下气体端面密封的瞬态响应；Miller等[6-7]先后采用直接数值求解法和半解析法研究了螺旋槽气体端面密封的动态特性；Ruan[8]基于摄动法研究了螺旋槽气体端面密封的追随性，并且采用直接数值计算法验证了求解结果；Blasiak等[9]采用直接数值求解法对比研究了不同槽型气体端面密封动态特性。众多研究主要集中在密封操作和结构参数对其动态特性的影响，虽然考虑了弹簧和补偿环用辅助密封圈(通常为O形圈)刚度和阻尼的影响，但均在给定值下进行的，并未进行系列化的优化研究。鉴于此，本文研究了弹簧和补偿环用O形圈刚度和阻尼对目前常见的三种气体端面密封(动压式密封、静压式密封以及动静压混合式密封)动态追随性的影响。

目前，气体端面密封动态特性有两种研究方法：一种是直接数值求解法(Direct Numerical Simulation Method,DNSM)[10-11]；另一种是线性化的数值求解方法，包括摄动法(Small Perturbation Method,SPM)[12]、步进法(Step Jump Method,SJM)[13]以及直接数频响应法(Direct Numerical Frequency Response Method,DNFRM)[14]。直接数值求解法虽然能够完全获得密封动态特性，但是数值求解耗时，且不利于动态特性影响因素参数化的设计研究，实践证明线性化的数值求解方法对于密封的动态特性研究也是准确和实用，因而本文基于摄动法进行弹簧和O形圈刚度和阻尼对气体端面密封追随性的影响研究。

1 密封结构及工作原理

气体端面密封结构简图如图1所示，动环固连于转轴，静环通过O形圈和弹簧安装在密封壳体中，O形圈提供辅助密封，弹簧提供闭合力。密封工作时可以在动环和静环端面间形成稳定的气膜，密封气膜具有刚度和阻尼特性，在阻止密封腔介质(压力为po)泄漏的同时，保证密封端面非接触运转，避免摩擦磨损，且具有较低的泄漏率。

1-动环;2-静环;3-螺旋槽;4-均压槽;5-节流孔;6-O形圈;7-弹簧;8-弹簧座;9-转轴

图2所示为三种不同结构的气体端面密封，图2(a)为动压式气体端面密封，在动环端面上加工有螺旋槽，依靠流体动压效应实现非接触运转；图2(b)为静压式气体端面密封，在静环端面上加工有节流孔和均压槽，二者相互连通，节流孔的作用是将外部阻封气(气源压力为ps，经过节流后压力变为pd)导入密封端面，提供流体静压承载能力，节流孔实际上产生流动阻力增加气膜的刚度和稳定性，均压槽的作用是将通过节流孔输入的阻封气在周向进行均布；图2(c)为动静压混合式气体端面密封，静环端面结构与静压式密封完全一致，在动环端面上加工有“鱼骨”形螺旋槽，动静压混合式密封同时具备动压式密封和静压式密封的特点。本文研究的参数如表1所示，包括密封结构参数、操作参数以及动环微扰幅值等。

(a) 动压式密封

(b) 静压式密封

(c) 动静压混合式密封

图2 密封端面结构

Fig.2 Ring geometry of gas face seal

2 追随性研究数学模型

为研究气体端面密封的追随性，将密封装置简化为弹簧-阻尼-质量系统(如图3所示)：密封气膜具有刚度(k)和阻尼(c)特性；O形圈具有阻尼(cs)特性，弹簧阻尼和O形圈阻尼相比可以忽略不计；弹簧和O形圈共同具有刚度(ks)特性，本文称为综合刚度，即两者刚度之和；密封环具有质量(m)特性。基于摄动法求解控制气膜压力分布的动态非线性Reynolds方程，得到气膜微扰压力，进而求解表征密封气膜动态特性的刚度和阻尼系数。在动环微扰下建立静环动力学方程，求解方程研究密封的动态追随性。由于本文目的是研究弹簧和O形圈刚度和阻尼对气体端面密封追随性的影响规律，因而基于摄动法进行气体端面密封追随性的详细数值求解过程这里不再叙述。

2.1 气膜润滑方程

控制密封端面间流体流动，且能计及小孔节流动静压混合作用，等温常黏度的可压缩二维柱坐标非稳态Reynolds方程为[15-16]

表1 密封分析参数

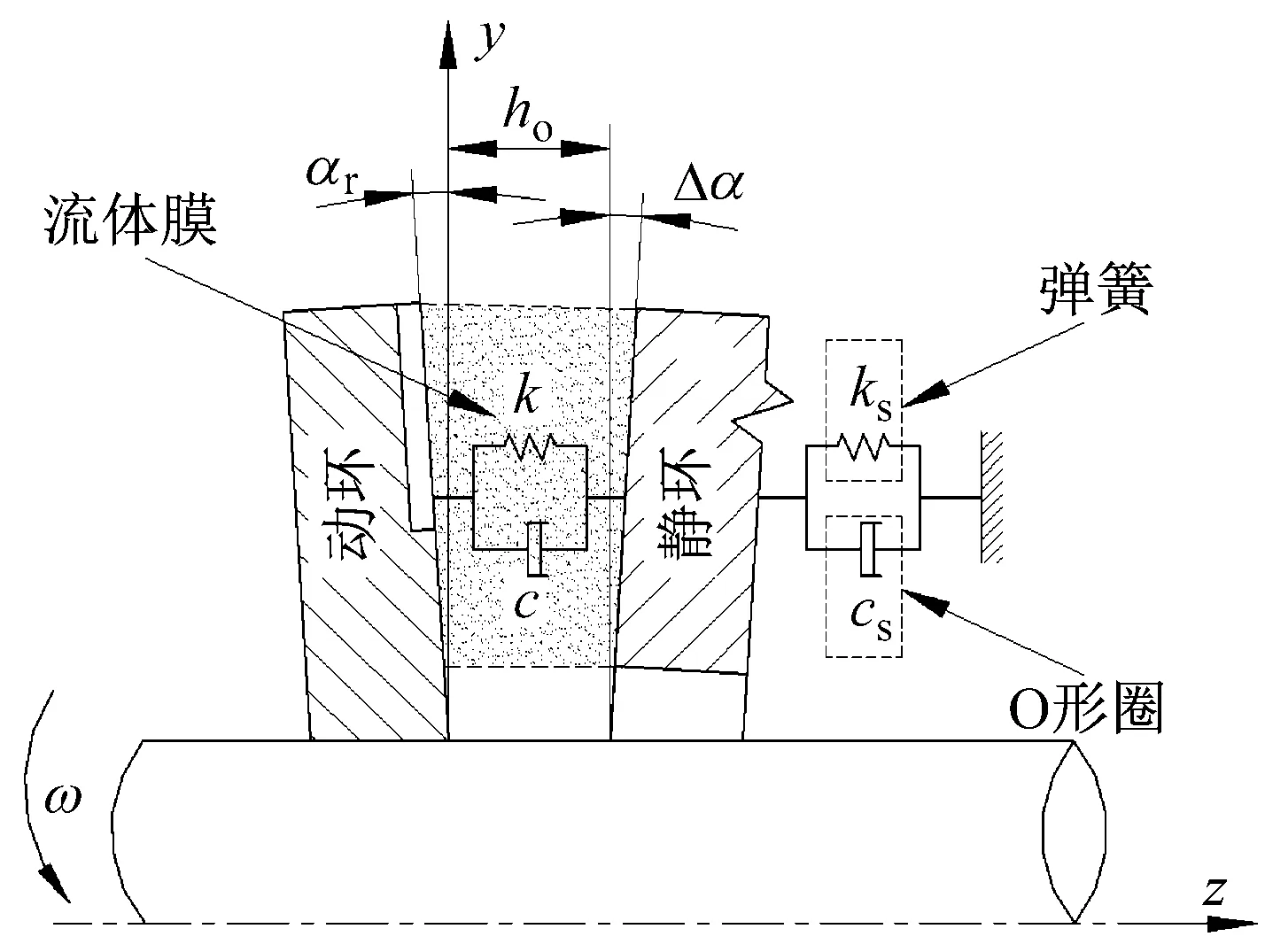
图3 气体端面密封简化模型

(1)

式(1)具有如下的边界条件

p(ri,θ,t)=pi

p(ro,θ,t)=po

p(r,0,t)=p(r,2π,t)

(2)

如图4所示，密封在扰动频率υ下有轴向和两个角向的微扰运动z(t)、α(t)、β(t)，式(1)中的瞬态气膜厚度为

h=ho+z(t)+rsinθα(t)-rcosθβ(t)+〈hg〉+〈hd〉

(3)

式中：ho为稳态气膜厚度；hg为动压槽深度；hd为均压槽深度；〈〉为只在槽区计入气膜厚度公式。

引入的微扰运动为简谐运动

z(t)=|Δz|eiυt,α(t)=|Δα|eiυt,β(t)=|Δβ|eiυt

(4)

微扰运动可在稳态气膜压力p0的基础上引起微扰压力Δp，利用一阶泰勒级数展开，瞬态气膜压力(含节流孔后压力)表示为

(5)

图4 密封动力学模型

2.2 气膜动态刚度和阻尼定义

微扰时气膜对静环的轴向力Fz和角向偏转力矩Mx、My的增量由微扰压力Δp引起，表达为

(6)

将Δp代入式(6)可得

(7)

由于气膜被视为具有刚度和阻尼特性，所以气膜对静环作用力的增量又有

(8)

式中：kij，cij(i，j=z,x,y)为气膜刚度和阻尼系数，负号代表气膜阻止微扰运动。

对比式(7)和式(8)，可得到由扰动压力所表达的气膜刚度和阻尼系数

(9)

气体端面密封气膜18个动态性能参数刚度和阻尼系数具有如下特征：

(1) 由两个角向(x和y)微扰引起的角向刚度和阻尼满足kxx=kyy、kxy=-kyx、cxx=cyy和cxy=-cyx的关系。

(2) 轴向和角向耦合刚度和阻尼系数(kzx、kzy、kxz、kyz、czx、czy、cxz、cyz)均为零。

(3) 气膜动态刚度和阻尼系数受扰动频率υ影响。

因此，气膜动态刚度和阻尼系数可以简化为

(10)

2.3 补偿环运动方程

在动环微扰运动的作用下，求解静环的响应运动，就可以得到气体端面密封的动态气膜厚度分布规律，研究密封追随性。由气膜动态特性系数满足的规律可知，静环的轴向运动和角向运动是解耦的，其在动环微扰作用下沿3个方向的运动方程为

(11)

(12)

式中：z、α和β分别为静环轴向响应以及扰x轴和y轴的角向响应；zr、αr和βr分别为动环轴向激励以及扰x和y轴的角向激励；m为静环质量；Ix，Iy为静环转动惯量；ks为弹簧和O形圈综合刚度;cs为O形圈阻尼；ksx和ksy为弹簧和O形圈的角向综合刚度;csx和csy为O形圈的角向阻尼，计算公式为

(13)

为求解式(11)和式(12)，需要知道气膜动态刚度和阻尼系数，气膜刚度和阻尼系数又受到静环微扰运动的频率υ影响，所以需要联立润滑方程进行迭代求解。庆幸的是式(11)和式(12)属于强迫运动的范畴，静环微扰运动的频率由动环激励频率决定，因此可以在给定动环激励频率的情况下，先求解润滑方程得到气膜动态刚度和阻尼系数，进而求解静环微扰运动，研究追随性。由于动环刚性地固连于转轴，所以激励频率和转轴角速度相等，故在此研究激励频率等于转轴角速度ω的情形。

3 研究结果分析

在扰动频率υ等于转轴角速度ω的情况下，数值求解了三种密封的气膜动态刚度和阻尼系数，如表2所示。

表2 密封刚度和阻尼系数

假定动环的激励形式为简谐振动zr=arzsin(ωt)，αr=arxcos(ωt)，βr=arysin(ωt)，其中arz、arx和ary分别为激励的幅值，基于表1中的参数研究了弹簧和O形圈的刚度和阻尼对三种气体端面密封追随性的影响规律。忽略静环响应运动与动环激励运动的相位差，以静环响应振动的幅值(分别为asz、asx和asy)大小来表征密封的追随性，静环响应振动的幅值越接近动环激励的幅值，密封追随性越好。

引入如下无量纲项

(14)

3.1 弹簧和O形圈综合刚度对密封追随性的影响

求解了弹簧和O形圈综合刚度对静环无量纲响应振动幅值的影响规律(由于密封端面的轴对称性，静环绕x轴和y轴的振动幅值相等)，如图5所示。由图可知当综合刚度小于107N/m时，三种密封静环的轴向和角向无量纲响应振动幅值基本保持不变；当综合刚度超过107N/m时，三种密封静环的各向无量纲响应振动幅值逐渐减小。这是由于当综合刚度的数量级接近或者超过密封气膜轴向刚度kzz的数量级时(动压式密封和动静压混合式密封为108N/m，静压式密封为107N/m)，密封振动主要发生在密封静环端面，而不是静环背面与弹簧接触处。因此，为了使密封具有良好的追随性，综合刚度不应该超过107N/m。通常情况下气体端面密封用弹簧和O形圈的综合刚度量级不会超过106N/m，因而密封不会因为刚度的选取不当而引起追随性不好。

为了进一步研究综合刚度对气体端面密封追随性的影响规律，分别求解了综合刚度数量级低于和等于107N/m时静环的响应运动，如图6所示。图6(a)～图6(e)为综合刚度等于5×106N/m时，静环的轴向和角向响应运动，图6(b)～图6(f)为综合刚度等于5×107N/m时，静环的轴向和角向响应运动。由计算结果对比分析可知，当综合刚度为5×106N/m时(数量级低于107N/m)，三种密封的静环针对动环简谐微扰在各个方向均可以提供良好的跟踪响应，响应运动与微扰运动同步，没有相位差，且简谐运动的幅值也基本相等。

(a) 轴向振幅

(b) 角向振幅

Fig.5 Influence of stiffness on dimensionless amplitudes of stator

当综合刚度为5×107N/m时(数量级等于107N/m)，三种密封的静环针对动环简谐微扰在各个方向均未能提供良好的跟踪响应，响应运动与微扰运动出现了相位差，且静环响应运动的幅值低于动环微扰运动的幅值。由计算结果亦可知，在同样参数下三种密封追随性的优劣为：动压式密封最好，动静压混合式密封次之，静压式密封最差。

3.2 密封圈阻尼对密封追随性的影响

求解了密封圈阻尼对静环无量纲响应振动幅值的影响规律，如图7所示。由图可知，三种密封静环各向无量纲响应振动幅值的变化规律一样，对于动压式和动静压混合式密封而言，当密封圈阻尼小于5×104N·s·m-1时，静环的各向无量纲响应振动幅值基本不变，随着密封圈阻尼的继续增大，无量纲响应振动幅值随之减小，密封的追随性变差。对静压式密封而言，当密封圈阻尼小于2×103N·s·m-1时，静环的各向无量纲响应振动幅值基本不变，随着密封圈阻尼的继续增大，无量纲响应振动幅值随之减小，密封的追随性亦变差。因此，为了使气体端面密封具有良好的追随性，动压式和动静压混合式密封补偿环用辅助密封圈的阻尼不应超过5×104N·s·m-1，而静压式密封不应超过2×103N·s·m-1。通常情况下气体端面密封用O形圈阻尼量级不会超过103N·s·m-1，因而密封不会因为O形圈阻尼选取不当而引起追随性不好。

(a) ks=5×106 N/m

(b) ks=5×107 N/m

(c) ks=5×106 N/m

(d) ks=5×107 N/m

(e) ks=5×106 N/m

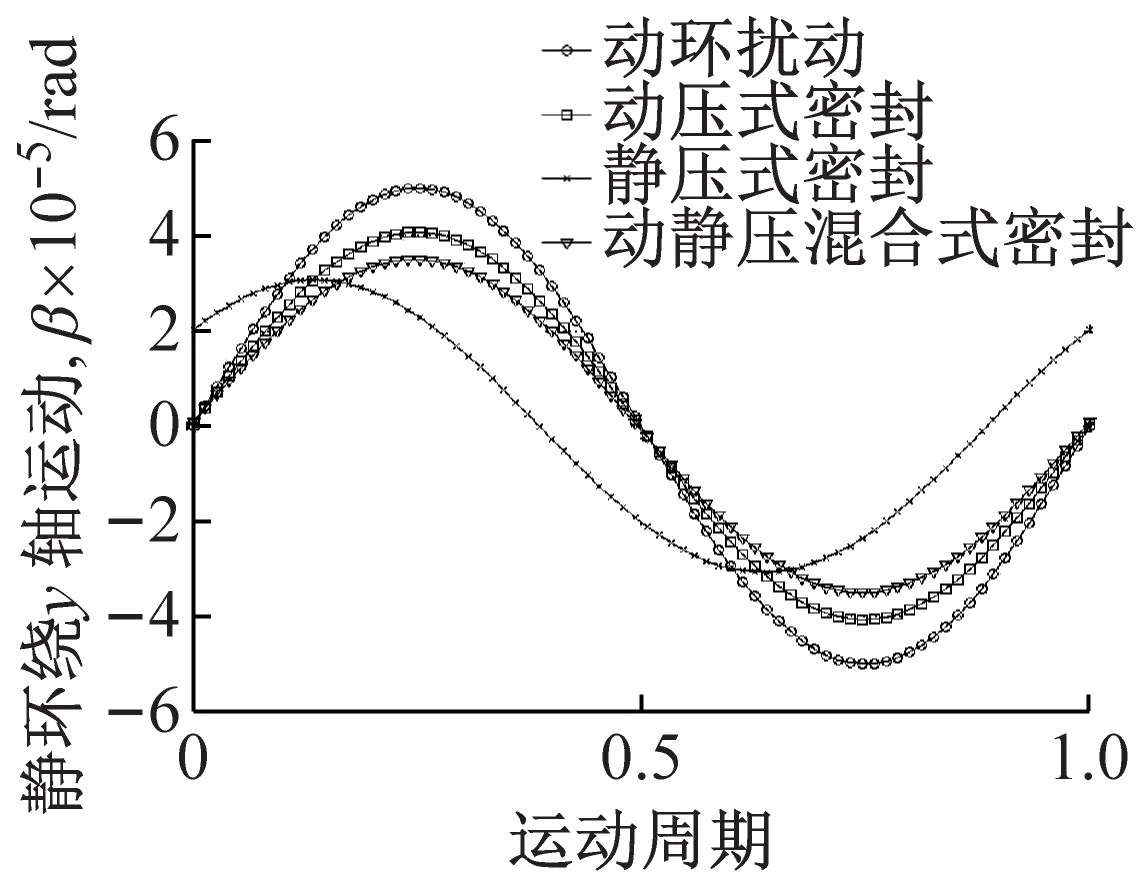
(f) ks=5×107 N/m

(a) 轴向振幅

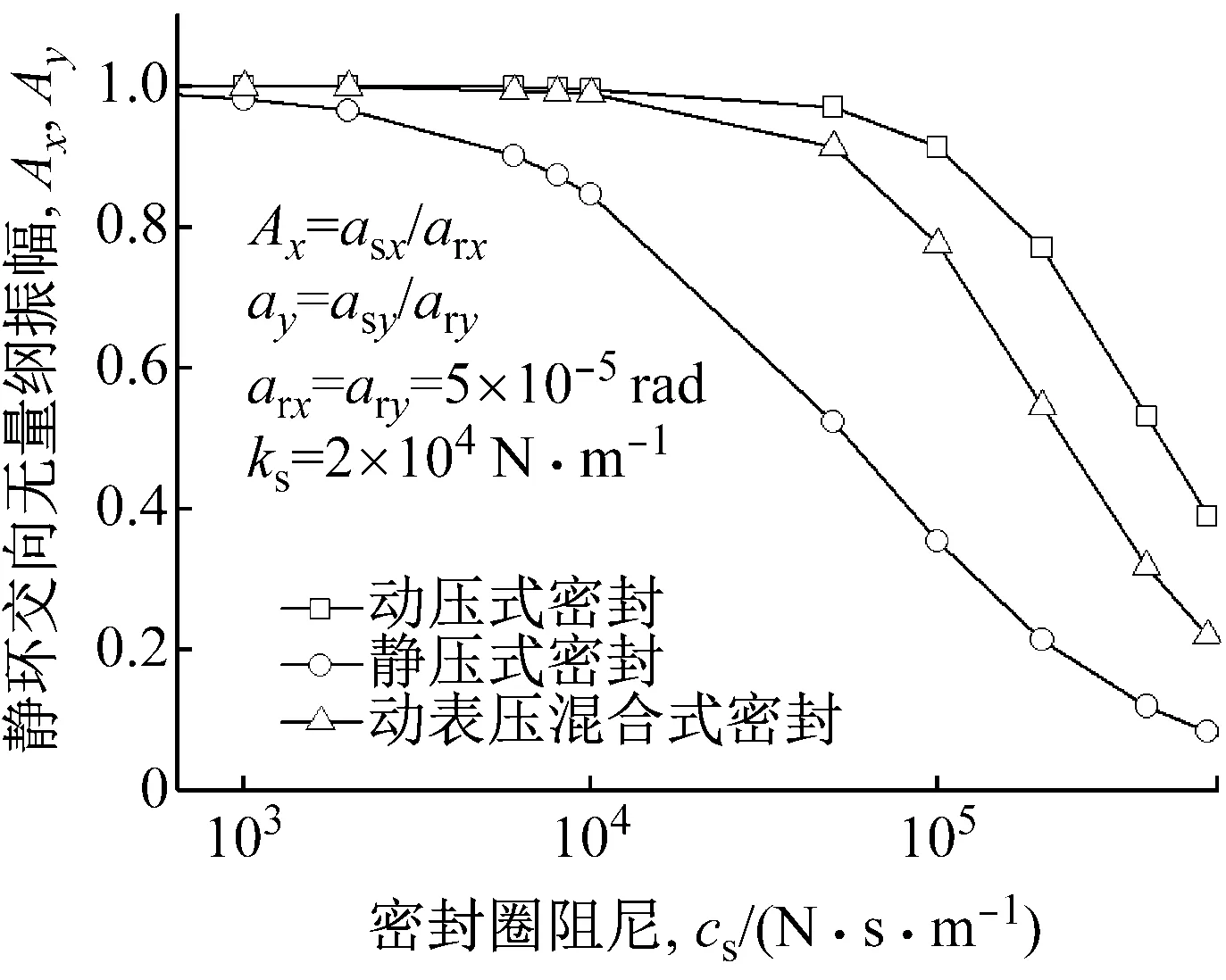
(b) 角向振幅

Fig.7 Influence of secondary seal damping on dimensionless amplitudes of stator

同样，为了进一步研究密封圈阻尼对气体端面密封追随性的影响规律，求解了不同数量级阻尼时静环的响应运动，如图8所示。图8(a)～图8(e)为密封圈阻尼等于2×103N·s·m-1时，静环的轴向和角向响应运动，图8(b)～图8(f)为密封圈阻尼等于1×105N·s·m-1时，静环的轴向和角向响应运动。由计算结果对比分析可知，当密封圈阻尼为2×103N·s·m-1时，三种密封的静环针对动环简谐微扰在各个方向均可以提供良好的跟踪响应，响应运动与微扰运动同步，没有相位差，且简谐运动的幅值也基本相等。当密封圈阻尼等于1×105N·s·m-1时，三种密封的静环针对动环简谐微扰在各个方向均未能提供良好的跟踪响应，响应运动与微扰运动出现了相位差，且静环响应运动的幅值低于动环微扰运动的幅值。由计算结果亦可知，在同样参数下三种密封追随性的优劣为：动压式密封最好，动静压混合式密封次之，静压式密封最差。

4 结 论

(1) 当弹簧和O形圈综合刚度低于某数量级时，三种密封在轴向和角向均能具有优异的追随性，随着综合刚度的增加，密封追随性随之变差。为了使气体端面密封具有良好的追随性，综合刚度不应该超过107N/m。

(a) cs=2×103 N·s·m-1

(b) cs=1×105 N·s·m-1

(c) cs=2×103 N·s·m-1

(d) cs=1×105 N·s·m-1

(e) cs=2×103 N·s·m-1

(f) cs=1×105 N·s·m-1

(2) 当辅助密封圈阻尼低于某数量级时，三种密封在轴向和角向均能具有优异的追随性，随着辅助密封圈阻尼的增加，密封追随性随之变差。为了使气体端面密封具有良好的追随性，动压式和动静压混合式密封补偿环用辅助密封圈的阻尼不应超过5×104N·s·m-1，而静压式密封不应超过2×103N·s·m-1。

(3) 在同样的操作条件下，螺旋槽密封追随性最好，动静压混合密封次之，静压密封最差。

[1] 张树强, 李双喜, 蔡纪宁, 等. 动静压混合式气体密封追随性及主动调控振动特性数值分析[J]. 航空学报, 2012, 33(7): 1336-1346.

ZHANG Shuqiang, LI Shuangxi, CAI Jining, et al. Numerical analysis for the tracking property and active regulation vibration characteristics of dynamic-hydrostatic hybrid gas seals[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(7): 1336-1346.

[2] 宋鹏云, 胡晓鹏, 许恒杰. 实际气体对T槽干气密封动态特性的影响[J]. 化工学报, 2014, 65(4): 1344-1352.

SONG Pengyun, HU Xiaopeng, XU Hengjie. Effect of real gas on dynamic performance of T-groove dry gas seal[J]. CIESC Journal, 2014, 65(4): 1344-1352.

[3] 刘向锋, 徐辰, 黄伟峰. 基于半解析法的极端工况干气密封动态特性研究与参数设计[J]. 清华大学学报(自然科学版), 2014, 54(2): 223-228.

LIU Xiangfeng, XU Chen, HUANG Weifeng. Analysis and parametric design of the dynamics of a dry gas seal for extreme operating conditions using a semi-analytical method[J]. Journal Tsinghua University (Natural Science), 2014, 54(2): 223-228.

[4] 丁雪兴, 陆俊杰, 刘勇, 等. 热耗散变形下干气密封系统轴向振动稳定性分析[J]. 振动工程学报, 2016, 29(1): 79-86.

DING Xuexing, LU Junjie, LIU Yong, et al. Stability analysis on axial vibration of dry gas seal system under the thermo-elastic deformation considering the thermal dissipation[J]. Journal of Vibration Engineering, 2016, 29(1): 79-86.

[5] GREEN I, BARNSBY R M. A simultaneous numerical solution for the lubrication and dynamic stability of noncontacting gas face seals[J]. Journal of Tribology, 2001, 123(2): 388-394.

[6] MILLER B A, GREEN I. Numerical formulation for the dynamic analysis of spiral-grooved gas face seals[J]. Journal of Tribology, 2001, 123(2): 395-403.

[7] MILLER B A, GREEN I. Semi-analytical dynamic analysis of spiral-grooved mechanical gas face seals[J]. Journal of Tribology, 2003, 125(2): 403-413.

[8] RUAN B. A semi-analytical solution to the dynamic tracking of non-contacting gas face seals[J]. Journal of Tribology, 2002, 124(1): 196-202.

[9] BLASIAK S, ZAHORULKO A V. A parametric and dynamic analysis of non-contacting gas face seals with modified surfaces[J]. Tribology International, 2016, 94: 126-137.

[10] RUAN B. Numerical modeling of dynamic sealing behaviors of spiral groove gas face seals[J]. Journal of Tribology, 2002, 124(1): 186-195.

[11] GREEN I, BARNSBY R M. A parametric analysis of the transient forced response of noncontacting gas coned face seals[J]. Journal of Tribology, 2002, 124(2): 151-157.

[12] ZIRKELBACK N, ANDRES L S. Effect of frequency excitation on force coefficients of spiral groove gas seals[J]. Journal of Tribology, 1999, 121(4): 853-863.

[13] ELROD H G, JR. MCCABE J T, CHU T Y. Determination of gas-bearing stability by response to a step-jump[J]. Journal of Lubrication Technology, 1967, 89(4): 493-498.

[14] MILLER B A, GREEN I. Numerical techniques for computing rotor-dynamic properties of mechanical gas face seals[J]. Journal of Tribology, 2002, 124(4): 755-761.

[15] 刘暾, 刘育华, 陈世杰. 静压气体润滑[M]. 哈尔滨: 哈尔滨工业大学出版社, 1990: 122-126.

[16] 刘雨川, 徐万孚, 陈国林, 等. 端面气膜密封的高性能端面结构[J]. 航空学报, 2000, 21(2): 187-190.

LIU Yuchuan, XU Wanfu, CHEN Guolin, et al. Face configuration with high performance for gas film face seal[J]. Acta Aeronautica et Astronautica Sinica, 2000, 21(2): 187-190.