截割厚度与截线距对镐型截齿破岩力学参数的影响
2018-02-27梁运培王清峰
梁运培, 王 想,, 王清峰
(1.重庆大学 煤矿灾害动力学与控制国家重点实验室,重庆 400044;2.中煤科工集团重庆研究院有限公司,重庆 400039)
机械切削方式以其高效的破岩优势被广泛用于采矿、石油天然气和地铁等地下工程领域。单个刀具破岩力学参数是计算工作机构扭矩及推进力的基础[1],同时也是研究破岩机械动态特性的重要参数[2-3]。作为重要的破岩工具,镐形截齿破岩力学参数(主要包括截割力和法向力)的研究备受国内外学者的关注。Evans[4]假设岩石拉力破坏建立了截割力的理论计算模型。Roxborouth等[5-6]考虑截齿与岩石之间的摩擦对Evans的截割力模型进行了改进。Goktan等[7]考虑刀面角的影响,提出了截割力的半经验公式。Bilgin等[8]基于岩石直线截割试验的相关数据,考虑岩石强度及截割厚度建立了力学参数的计算模型。Bao等[9]考虑截齿侵入岩石过程中的能量耗散,基于断裂力学建立了截割力模型。张倩倩等[10]基于试验及离散元方法,研究了截齿磨损对破岩载荷的影响。Wang等[11]使用主成分回归方法建立了截割力计算模型。
上述研究大都侧重于分析岩石物理力学性质对截齿破岩载荷的影响,截割厚度及截线距对力学参数影响规律的探讨尚显不足。以Evans理论为基础的模型中,截割力均与截割厚度的平方成正比,但Bilgin等的研究表明,无截槽影响的截割力、法向力与截割厚度之间有显著的线性关系。因此,力学参数与截割厚度的关系有待进一步研究。截线距对截割力和法向力的影响规律未见有详细的报道。法向力截割力比值常被用于法向力的预测,它与岩石强度密切相关,但截割厚度和截线距对该比值的影响未见有探讨。基于此,本文利用直线截割试验装置,在不同截割厚度和截线距的条件下,使用一种镐型截齿对砂岩进行截割试验,分析截割厚度和截线距对力学参数的影响。
1 试验设计
本试验采用直线截割方式,在每次的截割过程中截割厚度恒定不变。现有研究并未发现截割速度对截割力学参数有明显的影响[12]。He等[13]的试验表明,在截割速度为4~20 mm/s时,它对力学参数的影响较其它参数(如截割厚度)的影响很小,可以忽略。测试结果显示本试验所有截割速度均小于13 mm/s。
1.1 试验装置
岩石直线截割试验装置主要结构见图1,其主要包括位移传感器、滑块、滑轨、岩石盒、力传感器、截齿座、截齿、推进油缸、液压泵站和数据采集系统等。力传感器可以测试截割力和法向力(见图2),精度为1 N,截割力方向可最大测试力为100 kN,法向力方向可最大测试力50 kN。位移传感器为磁致位移传感器,测试范围为0~300 mm。液压泵站最高可提供60 MPa的压力,油缸最大推进力为89 kN。测试系统主要由采集卡、电源、电脑和采集软件组成,试验中数据采集频率设定为1 kHz。
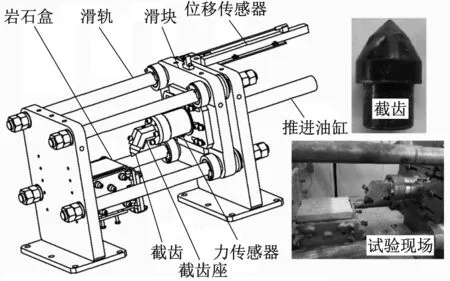
图1 岩石直线截割试验装置示意图
试验时,调整好截割厚度之后,用岩石盒周围的螺栓将岩石固定,然后通过力传感器底座水平滑动调节截线距离,以实现不同截线距的截割试验。
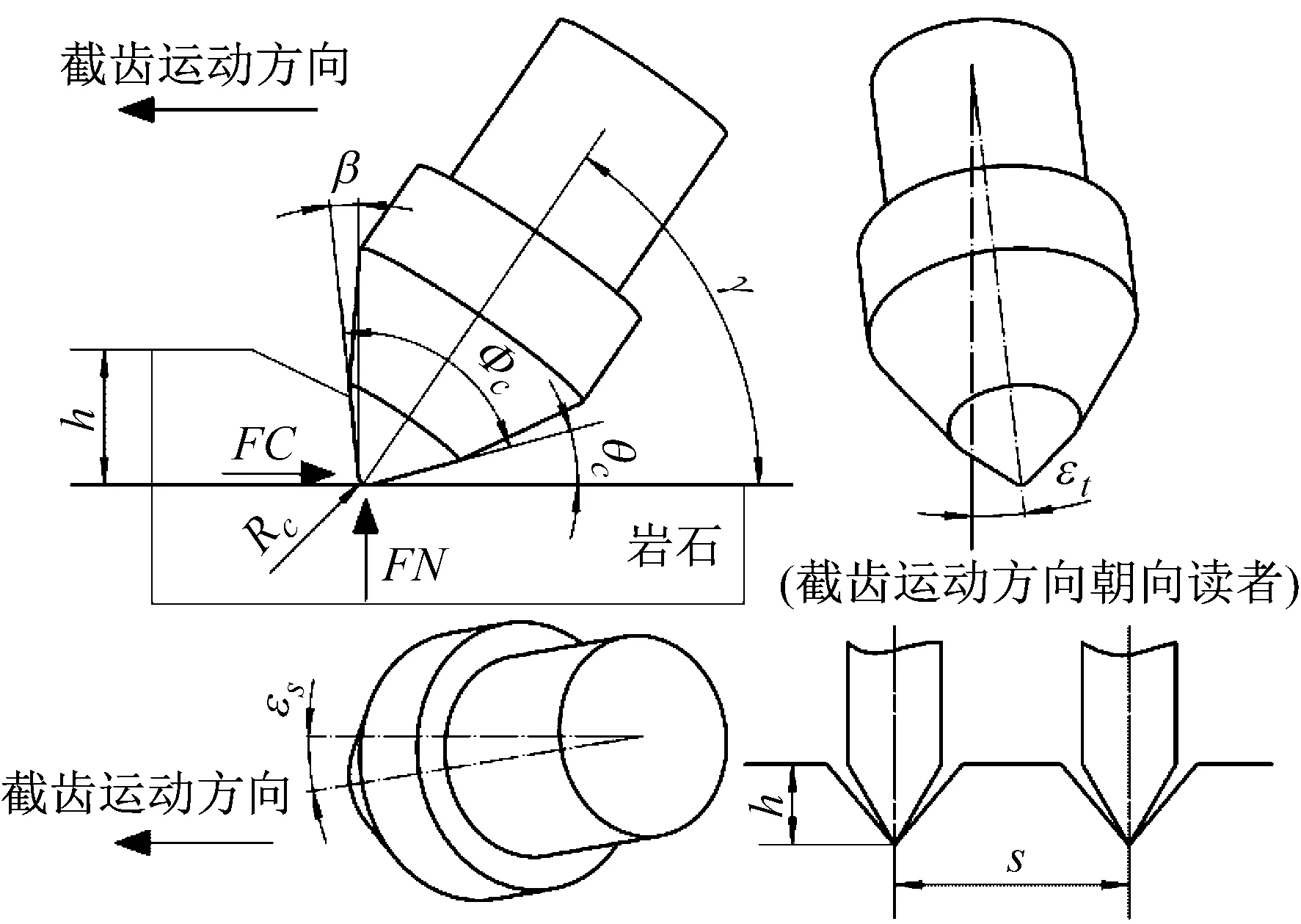
图2 镐型截齿相关截割参数示意图
Fig.2 Schematic diagram of relevant parameters of rock cutting using a conical pick
1.2 截齿及安装参数
试验使用的镐型截齿见图1,合金头锥角为80°,最大直径22 mm。镐型截齿截割参数示意图见图2。本试验中截齿的安装参数为:截割角55°,倾斜角0°,歪斜角0°,刀面角-5°,清理角为15°。
1.3 岩石物理力学性质
本文试验使用的是一种取自四川地区的青砂岩,试样尺寸为150 mm×150 mm×200 mm,均在商业采石场按尺寸要求加工成型。
测试的岩石物理力学性质参数包括抗压强度、抗拉强度、回弹硬度、弹性模量和泊松比等。岩石力学试验测试照片见图3。抗压强度采用φ50 mm×100 mm的标准试件(见图(3a)),对试验岩样随机取芯,试验重复6次,最终取其平均值。抗拉强度采用巴西劈裂法测试(见图3(b)),试件直径为φ50 mm,厚度与直径比值为0.5~0.7,试验重复6次,最终取其平均值。根据Bilgin等介绍的岩石回弹硬度的测试流程,使用冲击功能为2.207 J的回弹仪进行测试,在试件150 mm×150 mm的面上垂直冲击(见图(3b)),且随机抽取三个试样重复测试,最终平均值作为试验岩样的回弹硬度值。设计了一种平面截齿,在岩石直线截割装置上测试了岩石与刀具之间的摩擦角。岩石物理力学性质参数测试结果见表1。

(a)岩石抗压强度测试(b)岩石抗拉强度测试(c)岩石回弹硬度测试
图3 岩石力学参数测试 Fig.3 Rock mechanics tests 表1 岩石物理力学性质
2 试验参数设定及载荷评价指标
2.1 试验参数的设定
截线距s与截割厚度h的比值(s/h)是破岩机械工作机构设计较为常用的参数,且与岩石性质密切相关。Bilgin等在截割厚度为3~9 mm时的试验表明,s/h存在一个最优值,使破落单位体积岩石所消耗的能量最小,这个比值在2~5分布,且与岩石性质有关。基于此,本次试验的截割厚度h设定为3~18 mm,根据截割厚度h的不同,截线距s在6~48 mm变化。截线距与截割厚度比值(s/h)总体在1.33~6分布(见表2)。
2.2 载荷评价指标
常用描述载荷特征的参量包括载荷均值和载荷波动性系数(变差系数)[14-15]。设载荷F的第i个数值为Fi,均值为Fm,载荷波动性系数为LFC,其计算方法见式(1)。
(1)
式中:n为数据点个数。
统计学上,变差系数也叫标准差系数(本文定义为载荷波动性系数),是衡量比较不同类或平均值不相等数据的离散程度,它可以有效衡量载荷波动特性,其值越大载荷波动越严重。
3 试验结果分析
为了最大程度消除天然岩石的不均匀性和试验过程中的不确定因素对试验结果的影响,首先基于回弹硬度对岩石试样进行初步筛选,且每组截割试验重复3~8次,取其平均值作为最终结果。试验原始数据使用Matlab中的小波滤波工具箱进行去噪并计算其统计参数,最终结果见表2。
3.1 试验总体情况
试验大致分为两种截割模式:①截槽间互不影响,即在截割厚度一定的情况下,当截线距s较大时,截槽间岩石无法崩落,如图4(a)所示,即已有的截槽对截割无影响(本文称作无截槽影响),表2中前6组数据为无截槽影响时测试的数据。②截槽间互相影响,随着截线距s的减小,截槽间的岩块能形成有效崩落(图4(b)所示),这是破岩机械(如悬臂式掘进机,采煤机)工作机构破岩常见的截槽形式。对于本文使用的砂岩,试验发现当截线距与截割厚度s/h>6之后,截槽间将互不影响。
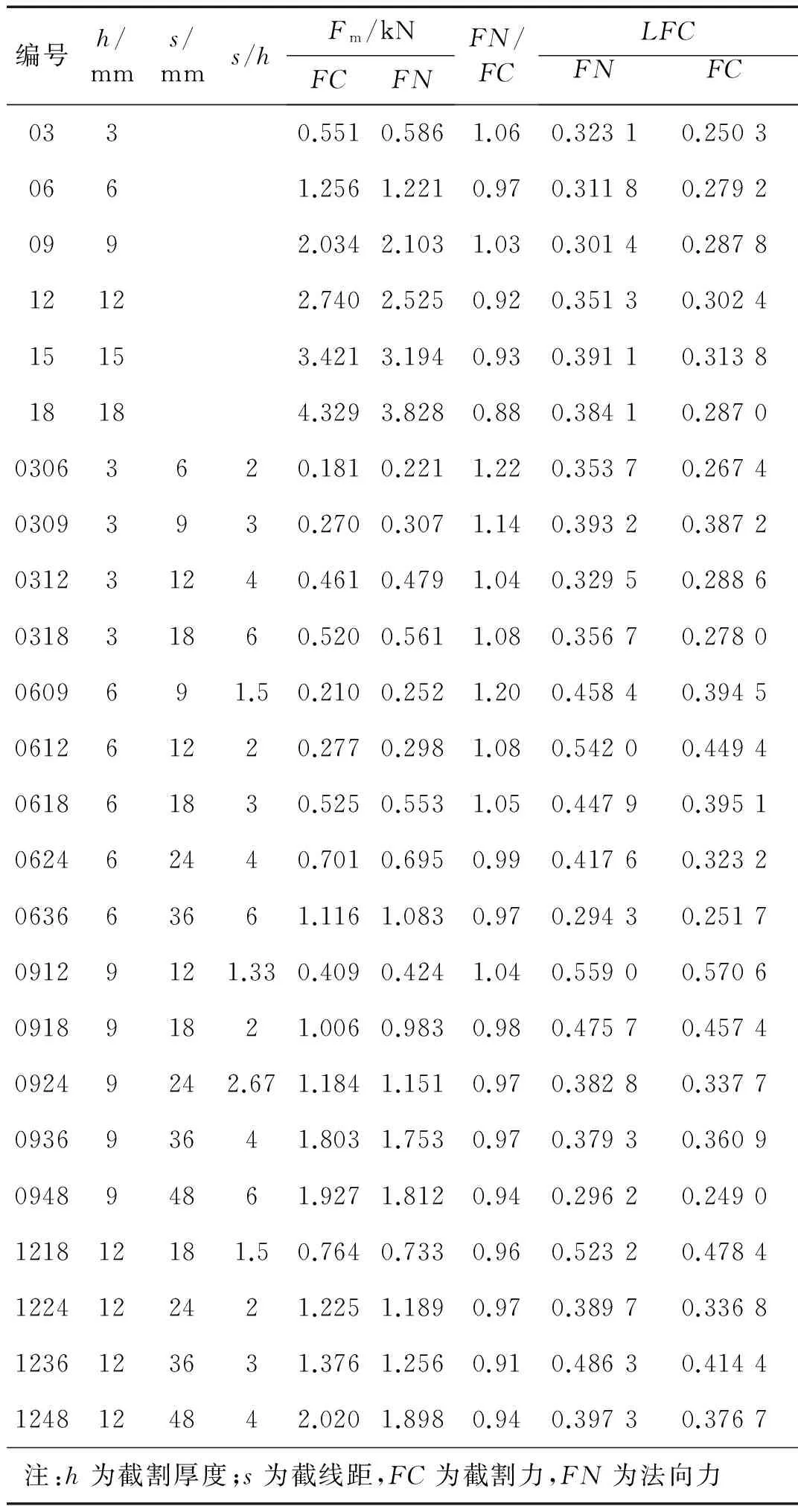
表2 岩石截割试验结果
图5给出了截割厚度h为12 mm时,无截槽影响条件下的截割力与法向力随着截割距离变化的载荷曲线。由图可以看出,截割力和法向力有明显的峰值且呈周期性出现,峰值即对应最大岩屑的崩落,峰值的大小和出现的周期大致相同,可以判断相同截割厚度条件下,崩落的最大岩屑粒度大致相同。
3.2 截割厚度对力学参数的影响
根据表2中的数据,使用单因素回归方法建立了截割力、法向力与截割厚度的关系,分别见图6、图7,法向力切削力比值与截割厚度的关系见图8。相关回归方程及统计参数见表3。

(a) 截槽间无影响

(b) 截槽间岩块崩落
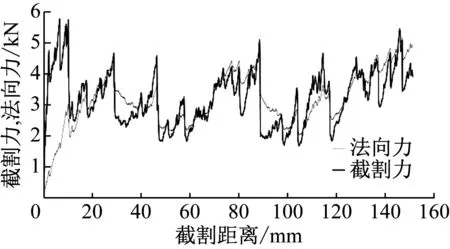
图5 镐型截齿截割载荷曲线
由图6、图7及表3中的统计参数可知,无截槽影响时,截割力、法向力与截割厚度之间有极强的线性关系(R2>0.99),并且在置信水平为95%时,具有统计学显著性(p<0.05)。同时,使用幂函数拟合同样可得到显著的统计学关系,无截槽影响截割力模型中截割厚度的幂值为1.141。在有截槽影响时,线性拟合与幂函数拟合表明:截割力、法向力与截割厚度之间具有统计学显著性,但决定系数R2均小于0.5,相关性较差,这说明截割力和法向力明显受到截槽间岩屑崩落的影响。单因素回归分析中,截割力、法向力的波动性系数与截割厚度之间未发现有显著的统计学关系。
图8所示,无截槽影响时,随着截割厚度的增加,法向力截割力比值呈直线减小(R2=0.768),与截割厚度为3 mm时相比,该比值在15 mm时约减小9.3%。
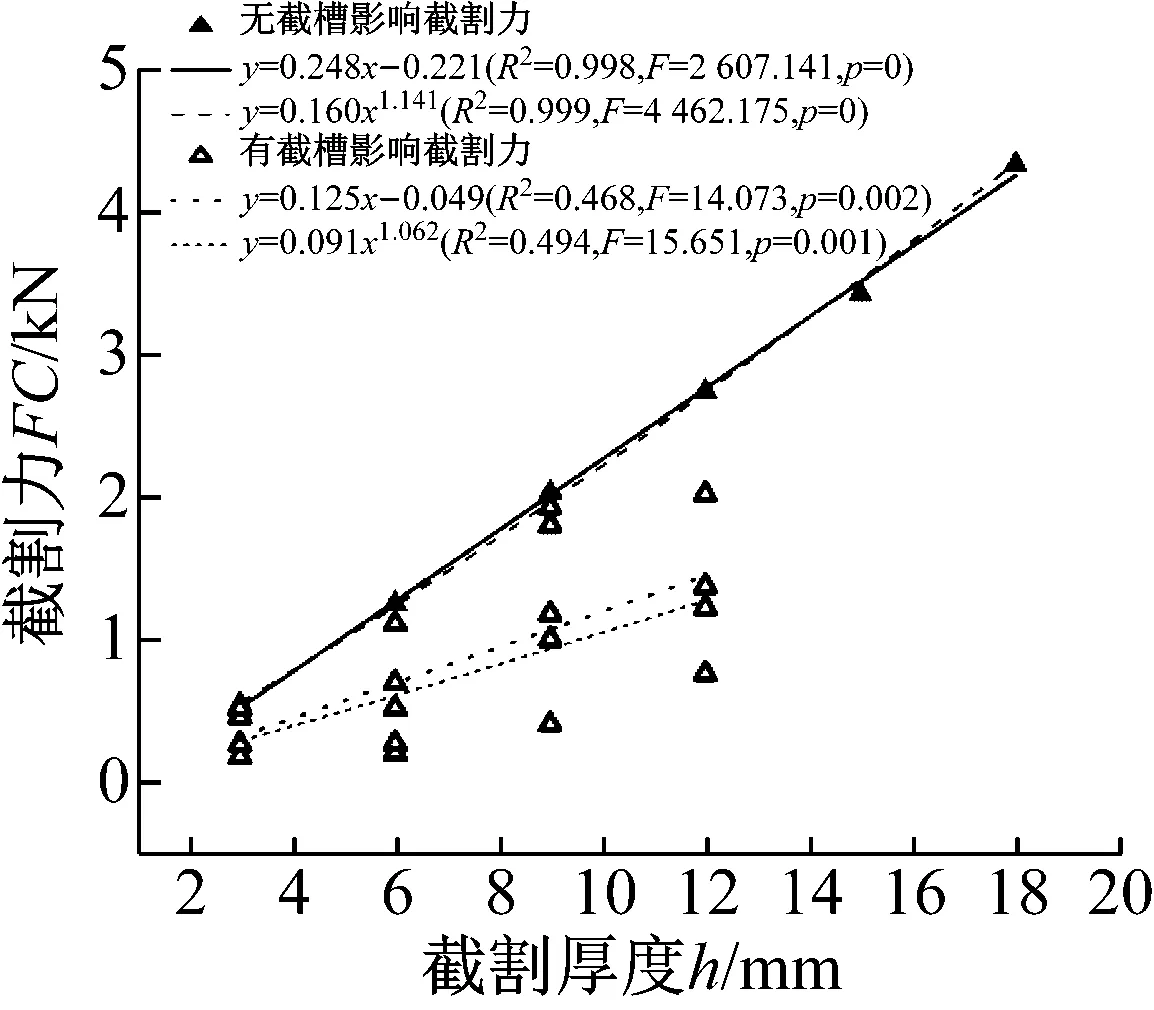
图6 截割力与截割厚度的关系
Fig.6 Relation between cutting force and depth of cut
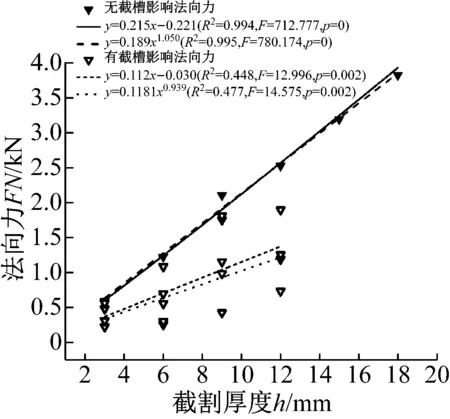
图7 法向力与截割厚度的关系
Fig.7 Relation between normal force and depth of cut
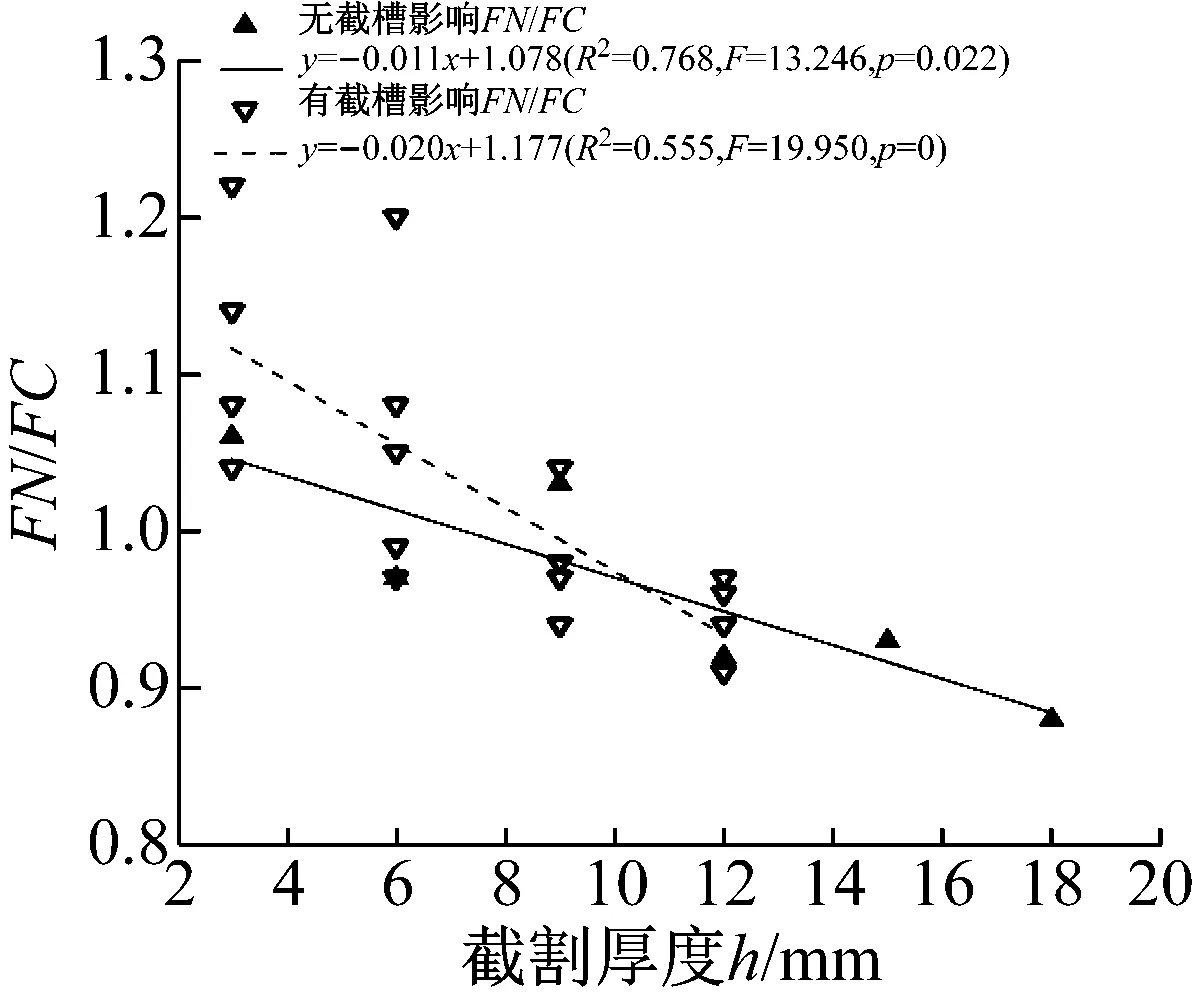
图8 FN/FC与截割厚度的关系
Fig.8 Relation betweenFN/FCand depth of cut
有截槽影响时,该比值与截割厚度之间的线性关系变弱(R2=0.555),说明该比值也受到截槽间岩屑崩落的影响。
3.3 截线距对力学参数的影响
有截槽影响时,截割力、法向力与截线距的关系见图9,法向力截割力比值与截线距的关系见图10。相关回归方程及统计参数见表4。
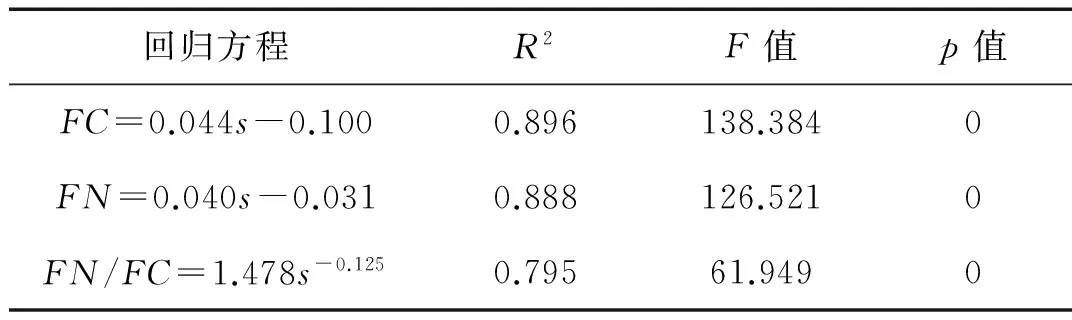
表4 载荷参数与截线距的关系
图9及表4中的统计参数表明,截割力、法向力与截线距之间有很强的线性关系(R2>0.89),且随着截线距的增大而增大。
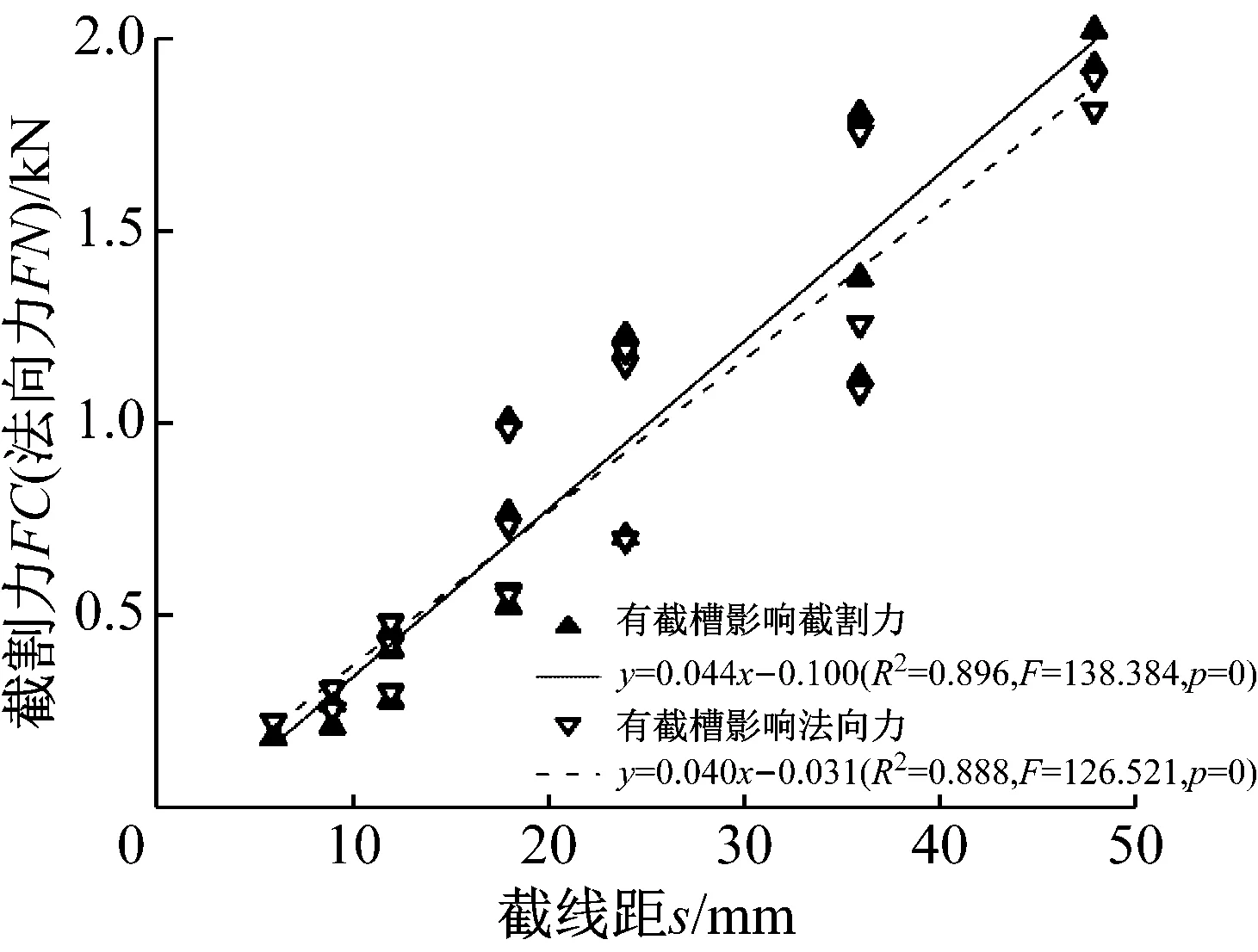
图9 力与截线距的关系
图10及统计参数显示,法向力截割力比值随着截线距的增加呈幂函数减小(R2=0.795)。相对于10 mm时,该比值在截线距40 mm时约减小15.9%。
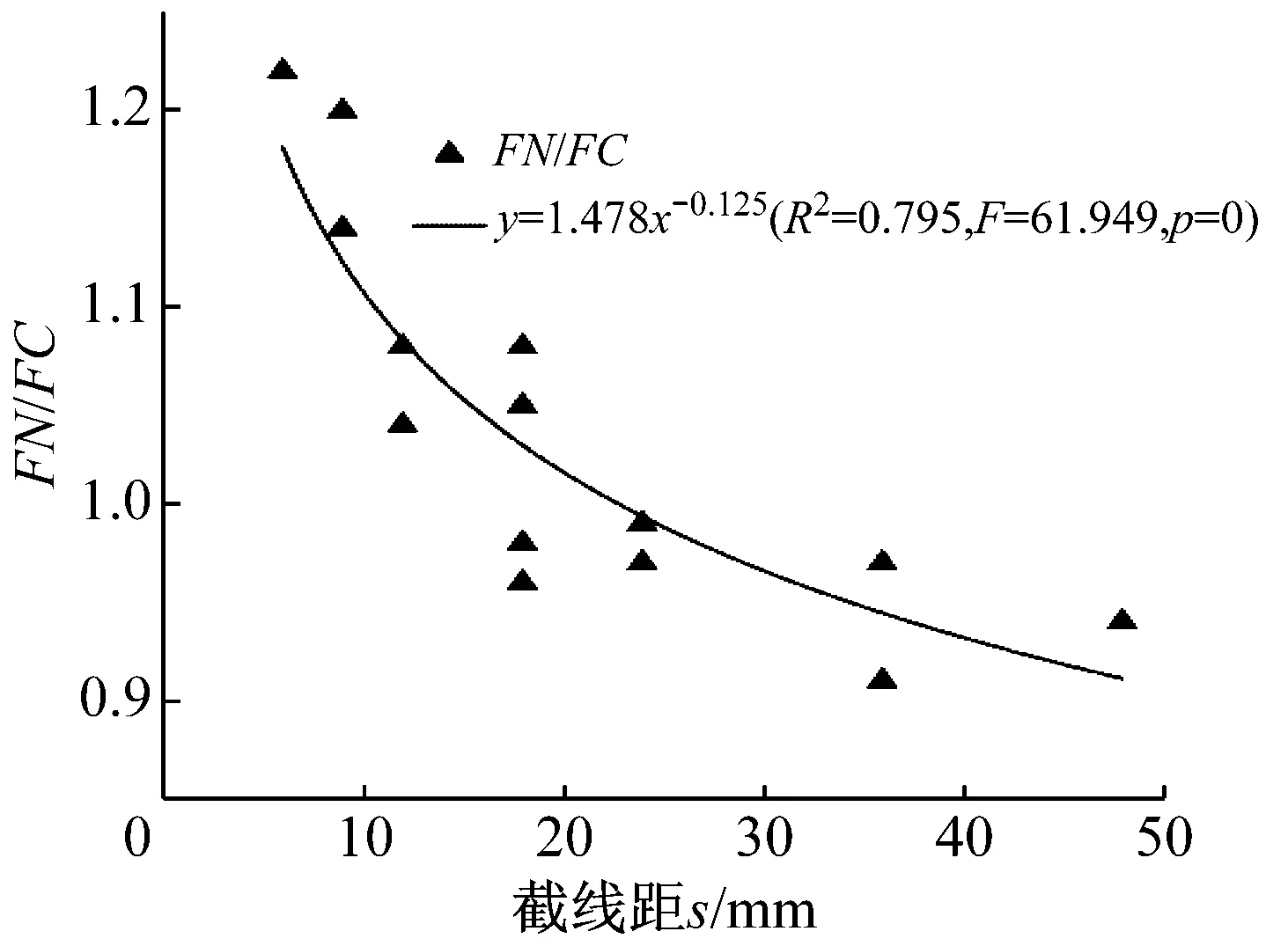
图10 FN/FC与截线距的关系
3.4 截线距与截割厚度的比值(s/h)对力学参数的影响
单因素回归分析表明,在置信水平为95%时,截割力、法向力以及法向力切削力比值与s/h之间没有显著的统计学关系。
由图11及表5中的统计参数可以看出,截割力、法向力的载荷波动性系数随着s/h的增大呈线性减小。这主要是因为,当s/h较小时,截槽间岩石更容易有大块岩屑崩落从而造成载荷波动较大,随着s/h的增大,截槽间的影响随之减小,甚至截槽间互不影响,载荷波动随之减小。
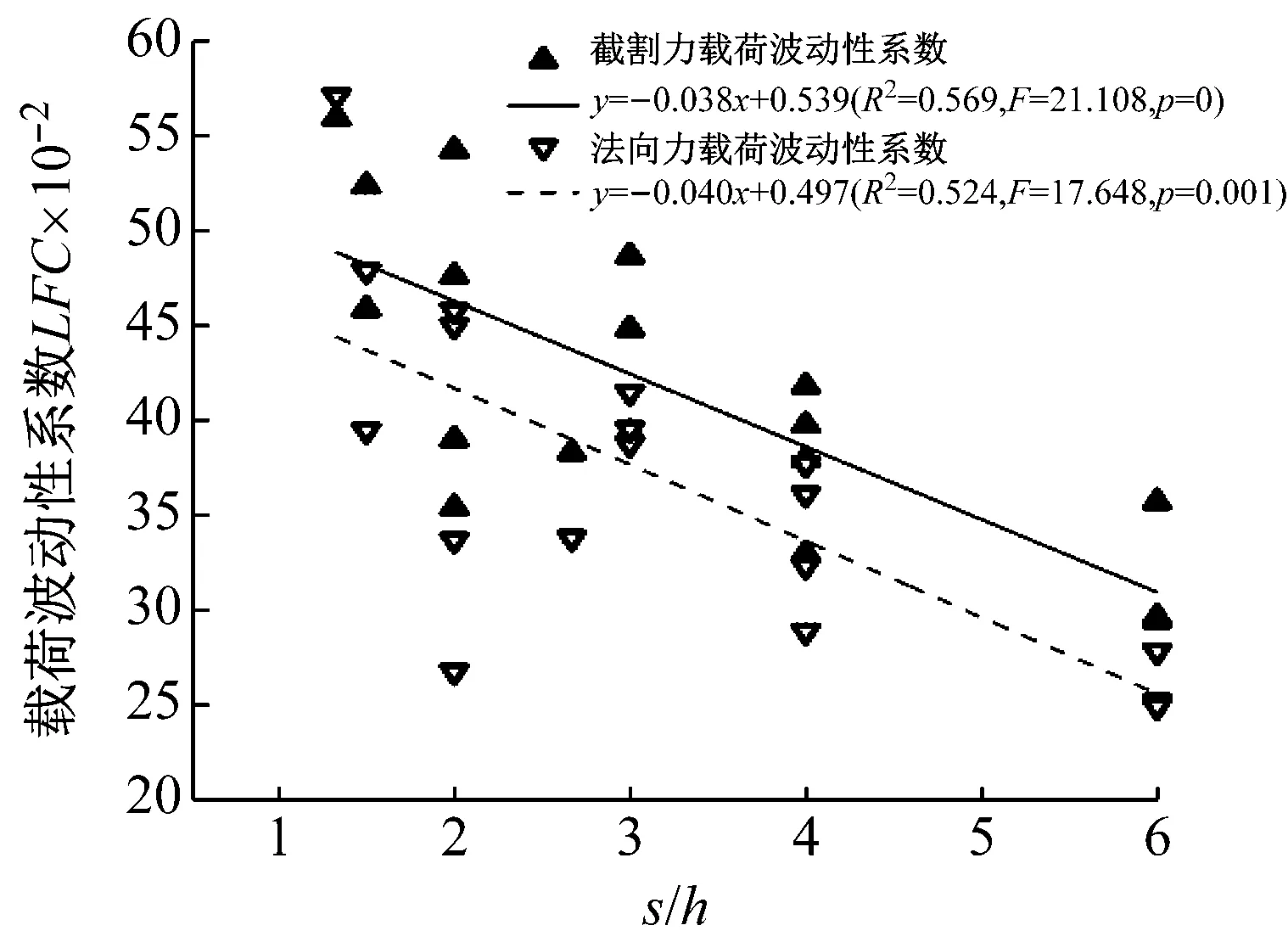
图11 载荷波动性系数与截线距截割厚度比值的关系
Fig.11 Relation between load fluctuation coefficient and the ratio of cut spacing to depth of cut
表5载荷波动性系数与截线距截割厚度比值的关系
Tab.5Relationbetweenloadfluctuationcoefficientandtheratioofcutspacingtodepthofcut

回归方程R2F值p值LFCFC=-0.038s/h+0.5390.56921.1080LFCFN=-0.040s/h+0.4970.52417.6480.001注:LFCFC为截割力载荷波动性系数;LFCFN为法向力载荷波动性系数
3.5 力学参数的多元线性拟合
单因素回归分析可知,相对无截槽影响的情况,截割力、法向力与截割厚度的关系在有截槽影响时相关性明显减弱,并且载荷波动性系数与截割厚度和截线距之间没有显著的统计学关系。这说明,截割厚度和截线距对力学参数都有显著的影响。因此,可以利用多元线性拟合方法,同时考虑截割厚度与截线距对力学参数的影响建立拟合方程。本文基于SPSS软件,使用多元线性拟合建立力学参数与截割厚度和截线距的关系。回归方程及统计参数见表6。
由于自变量之间可能存在较强的内在关系,多元线性回归分析中通常存在一定程度的多元共线性问题。若多元共线性比较严重,则会对变量产生很大影响,使回归方程的稳定性降低,或者得到不符合实际规律的回归系数。方差膨胀因子(Variances Inflation Factor,VIF)是衡量多元共线性程度的重要指标,若VIF=0则说明不存在多元共线性问题;0
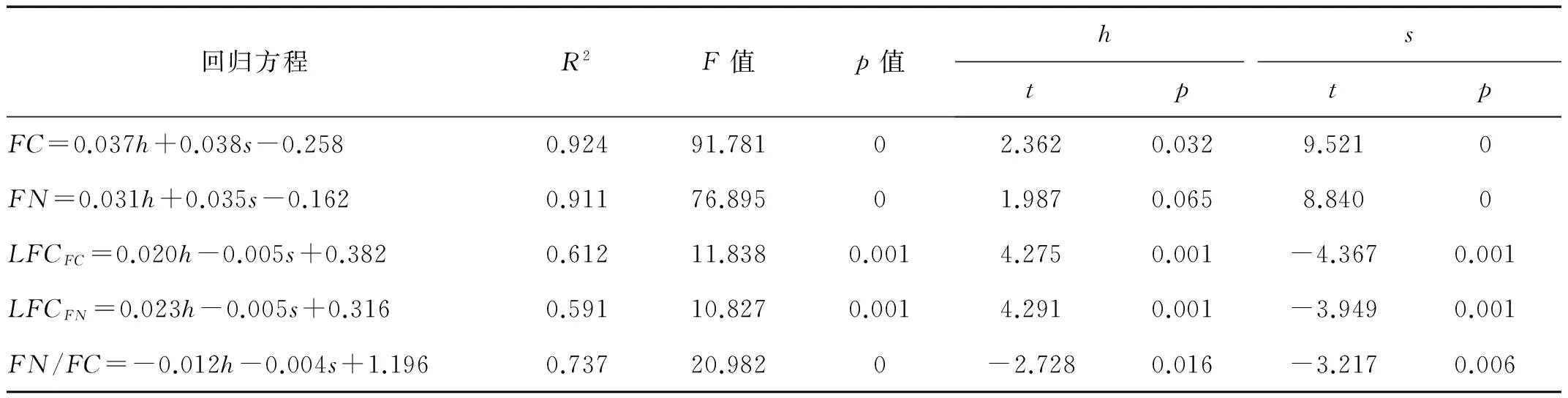
表6 载荷与截割厚度及截线距的关系
表6中的统计参数显示,截割力和法向力拟合方程的决定系数R2均大于0.9,表明截割力、法向力与截割厚度和截线距之间表现出极强的统计学关系。载荷波动性系数与截割厚度及截线距之间存在显著的统计学关系(R2=0.612,0.591)。从回归方程看,截割力、法向力的载荷波动性系数与截割厚度呈正比,与截线距呈反比。这主要是因为截割厚度越大越容易产生大的岩屑从而形成较大的载荷峰值,载荷波动越严重;截线距越小截槽间相互作用使岩屑更容易崩落,载荷波动也会越严重。
3.6 经典截割力理论公式性能比较
Evans,Roxborouth等,Goktan的截割力FCE、FCRL、FCG理论模型分别见式(2)~式(4)。根据表1中的岩石力学性质及表2中的截割参数,截割力理论计算结果见表7。
(2)
FCRL=
(3)
(4)
式中:σc为岩石抗压强度,MPa;σt为岩石抗拉强度,MPa;φ为截齿与岩石之间的摩擦角。
理论模型均未考虑截槽的影响,因此本文以无截槽影响的截割力实测值为基础对其预测性能进行比较。
图12给出了截割力实测值与理论预测值的关系。由统计参数可以看出,在置信水平0.95时,实测截割力与理论预测值之间有显著并且很强的线性关系(R2=0.966,p=0)。从表7中的数值及图12中直线的相对位置可以初步判断,Goktan等的理论模型过高的估计了截割力。表7中t检验的结果显示Evans,Roxborouth等以及Goktan的理论预测值在置信水平0.95时p值均大于0.05,可以判断预测值与实测值在统计学上没有显著区别。
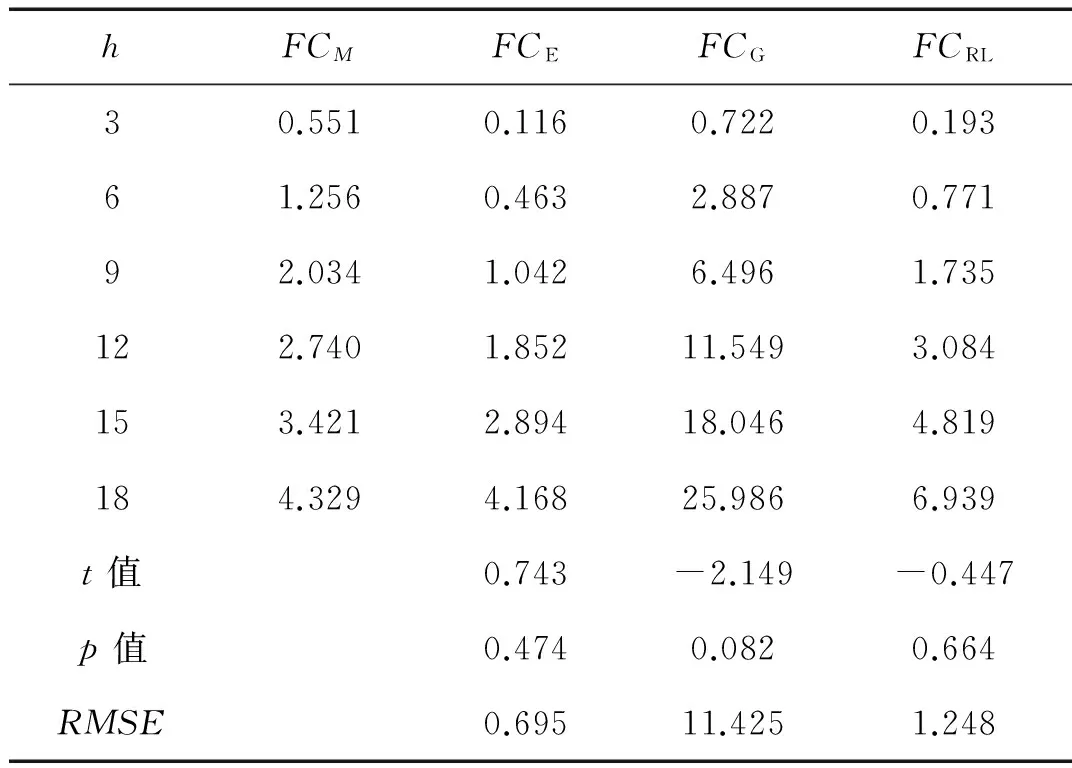
表7 截割力理论计算值和统计参数
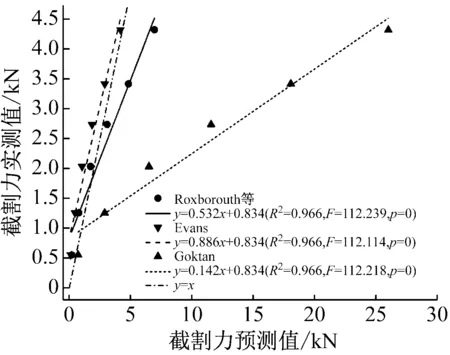
图12 截割力理论预测值与实测值得关系
均方根误差(Root Mean Square Error,RMSE)常被用于评价经验公式的预测性能,计算方法见式(5),各模型预测结果的RMSE值见表7。
(5)
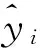
RMSE值越小说明预测性能越好,表7中RMSE的计算数值显示,Evans理论模型的预测性能最好,Roxborouth等理论模型次之,Goktan理论模型的预测性能较差。
4 结 论
在不同截割厚度、截线距条件下,对镐型截齿破岩进行了试验研究。利用回归分析研究了力学参数与截割厚度和截线距之间的关系。具体结论如下:
(1) 单因素回归分析表明。线性拟合与幂函数拟合均能很好的描述截割力、法向力与截割厚度之间的统计学关系。无截槽影响时,截割力、法向力与截割厚度之间存在极强的统计学关系;当有截槽影响时,相关性较弱;载荷波动性系数与截割厚度以及截线距之间没有显著的统计学关系。法向力截割力比值随着截割厚度的增加呈线性减小;截割力和法向力随着截线距的增加呈线性增加;法向力截割力比值随着截线距的增加呈幂函数减小;截割力、法向力与截线距截割厚度的比值(s/h)之间没有显著的统计学关系;载荷波动性系数与s/h之间存在显著的线性关系,且呈反比。
(2) 多元线性回归表明,截割力、法向力与截割厚度和截线距之间表现出极强的统计学关系;载荷波动性系数与截割厚度及截线距之间存在显著的统计学关系,且与截割厚度成正比,与截线距成反比。
(3) Evans的理论模型对截割力的预测性能最好,Roxborouth等的理论模型次之,Goktan的理论模型过高的估计了截割力的值,预测性能较差。
[1] BILGIN N, COPUR H, BALCI C. Effect of replacing disc cutters with chisel tools on performance of a TBM indifficult ground conditions[J]. Tunnelling and Underground Space Technology, 2012, 27(1): 41-51.
[2] 朱才朝, 冯代辉, 陆波,等. 钻柱结构与井壁岩石互作用下系统耦合非线性动力学研究[J]. 机械工程学报, 2007, 43(5): 145-149.
ZHU Caichao, FENG Daihui, LU Bo, et al. Nonlineaer study on dynamic action of integrated drill string-well rock system[J]. Chinese Journal of Mechanical Engineering, 2007, 43(5): 145-149.
[3] 王清峰, 朱才朝, 史春宝, 等. 变载荷工况下钻机动力头传动系统动态特性[J]. 振动与冲击, 2014, 33(17): 18-23.
WANG Qingfeng, ZHU Caichao, SHI Chunbao, et al. Dynamic characteristics of a drilling rig’s driving head transmission system under varying working environment[J]. Journal of Vibration and Shock, 2014, 33(17): 18-23.
[4] EVANS I. A theory of the cutting force for point-attack[J]. International Journal of Mining Engineering, 1984, 2(1): 63-67.
[5] ROXBOROUGH F F, LIU Z C. Theoretical considerations on pick shape in rock and coal cutting[C]∥Proceedings of the 6th Underground Operator’s Conference. Kalgoorlie: [s.n.], 1995: 189-193.
[6] GOKTAN R M. A suggested improvement on Evans cutting
theory for conical picks[C]∥Proceedings of the 4th International Symposium on Mine Mechanization and Automation. Brisbane: [s.n.], 1997: 57-61.
[7] GOKTAN R M, GUNES N. A semi-empirical approach to cutting force prediction for point attack picks[J]. The Journal of the South African Institute of Mining and Metallurgy, 2005, 105(4): 257-263.
[8] BILGIN N, DEMIRCIN M A, COPUR H, et al. Dominant rock properties affecting the performance of conical picks and the comparison of some experimental and theoretical results[J]. International Journal of Rock Mechanics and Mining Sciences, 2006, 43(1): 139-156.
[9] BAO R H, ZHANG L C, YAO Q Y, et al. Estimating the peak indentation force of the edge chipping of rocks using single point-attack pick[J]. Rock Mechanics and Rock Engineering, 2011, 44(3): 339-347.
[10] 张倩倩, 韩振南, 张梦琦, 等. 冲击载荷作用下锥形截齿磨损的试验和数值模拟研究[J]. 振动与冲击, 2016, 35(13): 58-165.
ZHANG Qiangqian, HAN Zhennan, ZHANG Mengqi, et al. Tests and simulation for wear of conical pick under impact load[J]. Journal of Vibration and Shock, 2016, 35(13): 58-165.
[11] WANG X, LIANG Y P, WANG Q F, et al. Empirical models for tool forces prediction of drag-typed picks based on principal component regression and ridge regression methods[J]. Tunnelling and Underground Space Technology, 2017, 62:75-95.
[12] NISHIMATSU Y. The mechanics of the rock cutting[J]. International Journal of Rock Mechanics and Mining Sciences, 1972, 9(2): 261-270.
[13] HE X, XU C. Specific energy as an index to identify the critical failure mode transition depth of rock cutting[J]. Rock Mechanics and Rock Engineering, 2016,49(4):1461-1478.
[14] 李晓豁, 李婷, 焦丽, 等. 滚筒采煤机截割载荷的模拟系统开发及其模拟[J]. 煤炭学报, 2016, 41(2): 502-506.
LI Xiaohuo, LI Ting, JIAO Li, et al. Development of cutting load simulation system and its simulation study on drum shearer[J]. Journal of China Coal Society, 2016, 41(2): 502-506.
[15] 王想, 王清峰, 谭正生. 纵轴式截割头截齿布置对截割载荷规律的影响[J]. 工程设计学报, 2012, 19(1): 39-42.
WANG Xiang, WANG Qingfeng, TAN Zhengsheng. The effects of picks arrangement on loads law of rock cutting with longitudinal cutting head[J]. Chinese Journal of Engineering Design, 2012, 19(1): 39-42.
