不同类型单层球面网壳结构弹性屈曲分析研究
2020-06-15潘晓娟安徽省建筑设计研究总院股份有限公司安徽合肥230601
潘晓娟 (安徽省建筑设计研究总院股份有限公司,安徽 合肥 230601)
0 前言
随着我国科学技术水平的不断提升,大跨度空间结构以其优异的特性广泛应用于各类大型体育馆、航站楼、展览馆等建筑中,此类建筑多为当地标志性建筑,担负着巨大使命,它不仅是当地经济水平和人文和谐的象征,同时在人们遭受重大自然灾害时也肩负着临时避难场所的重任,因此如何科学合理的设计此类结构,保证结构的安全性至关重要。
然而,对于单层球面网壳结构,随着网壳跨度的增大,单层球面网壳结构的稳定性问题越来越突出[1-3]。网壳结构的稳定性可按几何非线性的有限元法进行计算,而薄壳的屈曲问题就是其中一种几何非线性问题[4-8]。通常情况下网壳结构的屈曲分析方法有2种,即弹性屈曲分析和非线性屈曲分析。弹性屈曲分析又称之为特征值屈曲分析,其目的在于得到使结构变的不稳定时的屈曲荷载,即临界屈曲荷载,以便评估网壳的承载能力[9-14]。本文以相同跨度及杆件截面尺寸的K6型、肋环型、肋环斜杆型三类不同形式的单层球面网壳结构为例,分别分析了3种不同类型的网壳的自振频率及失效模态,从而对三类网壳的临界屈曲荷载进行对比分析。
1 有限元计算模型
为了研究网壳杆件的布置形式对单层球面网壳结构的临界屈曲荷载及失效模态的影响,3种网壳模型跨度均为60m,矢高比取1/4,结构分频数为8,各杆件截面尺寸如表1所示。
利用ANSYS有限元软件进行分析时,单元类型选用BEAM 188单元,材料模型选用Linear Isotropic,三类有限元模型如图1~图3所示。

图1 K6型单层球面网壳

图2 肋环型单层球面网壳

图3 肋环斜杆型单层球面网壳
2 特征值屈曲分析
当结构处于屈曲状态时,如果荷载进一步增加,则结构位移将发生较大变化,从一种平衡状态跳跃到另一种状态,因此,在进行网壳结构特征值屈曲分析时,其特征值屈曲经典方程为:

其中,[K]为单元弹性刚度矩阵,[Kcr]为与参考荷载相对应的初始应力刚度矩阵,λ为特征值屈曲荷载因子,{φ}为结构的位移特征矢量,是结构失稳的特征值屈曲模态形状。
2.1 计算模型频率分析
利用有限元分析软件,通过上述特征方程分别计算了三类网壳结构的前三阶特征值进行分析对比,具体数值如表2所示。
由表2分析可知,K6型单层球面网壳结构第一阶频率最小,为75912,即其临界屈曲荷载为75912N;肋环型单层球面网壳结构第一阶频率最小,为14018,即临界屈曲荷载为14018N;肋环斜杆型单层球面网壳结构第一阶、第二阶频率最小,均为106070,即临界屈曲荷载为106070N。分析可知,肋环斜杆型单层球面网壳结构临界屈曲荷载最大,肋环型最小,K6型单层球面网壳处于中间,其中,肋环斜杆型临界屈曲荷载为K6型单层球面网壳结构的1.4倍,为肋环型网壳临界屈曲荷载的7.6倍,由此可知网壳斜杆按肋环斜杆型网壳布置方式可大大提高网壳结构的临界屈曲荷载。

网壳结构杆件截面尺寸 表1

不同类型单层球面网壳结构特征值 表2
2.2 网壳模态分析

图4 K6型单层球面网壳屈曲模态

图5 肋环型单层球面网壳屈曲模态

图6 肋环斜杆型单层球面网壳屈曲模态
模态是弹性结构固有的、整体的特性,通过模态分析可以研究结构在某一易受影响的频率范围内的各阶主要模态的特性,据此可以预言结构在此频段范围内各种振源作用下产生的实际振动响应,因此,模态分析是结构动态设计的重要方法,尤其是对于大跨度空间结构。
三类单层球面网壳结构的三阶频率对应的振动模态分别如图4~图6所示。由图4的三阶模态分析可知,第一阶模态网壳结构第六环变形较大,竖向最大位移为1.32m;第二阶模态第五、七环变形最大,竖向最大位移为1.32m;第三阶模态第二、四、六三环变形较大,竖向位移最大为1.55m。图5为肋环型单层球面网壳结构的三阶屈曲模态,分析可知第一阶模态以网壳结构对称轴为界,左半部分向上变形较大,右半部分向下变形较大,最大位移为1.33m;第二阶模态,网壳环向及径向整体变形较大,最大位移为1.33m;第三阶模态,网壳结构为不对称变形,整体变形较大,且有扭曲变形,最大位移为1.01m。图6为肋环斜杆型单层球面网壳结构的三阶振动模态,第一、二阶频率及模态相同,网壳结构第四、五、六、七、八环沿网壳径向整体发生较大变形,尤其是斜杆变形较大,整体变形较规则,网壳竖向最大位移为1.25m;第三阶模态,网壳结构第六、八环整体结构沿径向变形较大,其竖向最大位移为1.29m。通过对比分析三类网壳的弹性屈曲模态,得到了屈曲状态下结构的真实变形,分析可知,在相同工况下,肋环斜杆型单层球面网壳结构稳定性大于K6型单层球面网壳,K6型单层球面网壳结构稳定性大于肋环型网壳结构。
2.3 网壳结构矢跨比对屈曲临界荷载的影响分析
以肋环斜杆型单层球面网壳结构为例,研究了网壳结构的矢跨比对其屈曲临界荷载的影响。在其他条件不变的情况下,分别取矢跨比为 1/4、1/5、1/6、1/7、1/8的网壳结构进行研究,通过有限元分析得到第一阶屈曲模态所对应的屈曲临界荷载曲线如图7所示。从图7可知,随着肋环斜杆型单层球面网壳结构的矢跨比增大,屈曲临界荷载增大,在肋环斜杆型单层球面网壳矢跨比较小的时候,其屈曲临界荷载要大于较大矢跨比的K6型单层球面网壳结构的第一阶屈曲模态所对应的屈曲临界荷载。从图7的整体变化规律可知,网壳结构的矢跨比对肋环斜杆型网壳结构第一阶屈曲模态对应的屈曲临界荷载影响较大。
2.4 带下部钢管柱的网壳结构屈曲分析
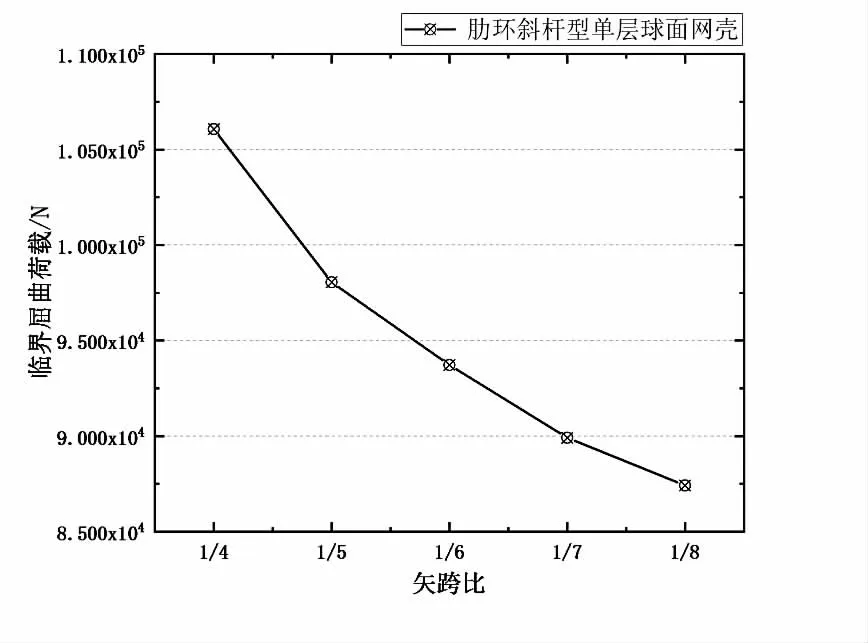
图7 不同矢跨比下屈曲临界荷载
带下部钢管柱的上部单层网壳结构尺寸与前面K6型单层球面网壳结构尺寸相同,下部立柱采用400×12mm的钢管。
结构在竖向荷载作用下的三阶阵型分别如图 8的(a)、(b)、(c)所示,第一阶模态的竖向最大位移为1.4m,第二阶模态的最大竖向位移为1.43m,第三阶模态的最大竖向位移为1.42m,与不带下部钢管柱的K6型单层球面网壳的竖向位移相比均有所增大,其中第三阶模态增大最多,为0.13m,第二阶模态增大0.11m,第一阶模态增大0.11m。带下部钢管柱的网壳结构,三阶模态对应的屈曲临界荷载分别为 23072N、27733N、27829N,与不带下部钢管柱的K6型单层球面网壳相比,屈曲临界荷载分别降低了69.6%、63.5%和63.4%。

图8 带下部钢管柱K6型单层球面网壳屈曲模态
3 结论
本文利用ANSYS软件对相同跨度及杆件截面尺寸的K6型单层球面网壳结构、肋环型单层球面网壳结构、肋环斜杆型单层球面网壳结构进行了弹性屈曲分析,主要得到了如下结论:
①相同荷载工况和相同跨度及相同杆件截面情况下,三类网壳结构的临界屈曲荷载从大到小依次为肋环斜杆型网壳、K6型单层网壳和肋杆型单层球面网壳;
②依据模态分析结果可知,肋环斜杆型单层球面网壳结构整体性较其他两类网壳良好,整体变形较规则;
③通过对比分析每一类网壳结构的屈曲模态,分析可知肋环斜杆型单层球面网壳结构整体稳定性最好,肋环型较差,K6型单层球面网壳结构介于两者之间。
④通过对带下部钢管柱的网壳及不带下部钢管柱的K6型单层球面网壳结构对比可知,K6型落地式网壳屈曲临界荷载大约是带钢管柱的网壳结构的屈曲临界荷载的2.7~3.3倍。
