四个聚焦,让课堂问题设置更有效
2018-02-14何丽结
何丽结


【摘要】 数学学习是学生主动面对问题,积极进行主体探究、推测、证明的活动.在这一过程中,问题是教学的核心,问题的设置直接影响学生整个学习过程.如何有效设计促进学生主动参与、深入探究、深度思考的好问题?通过课堂观察和实践发现,在问题设置方面聚焦学生“需掌握什么、有什么困惑、遇什么障碍、能获得什么”四个方面能让课堂问题设置更有效.
【关键词】 问题设置;聚焦;掌握;困惑;障碍;获得
课堂教学是培养学生核心素养的主要阵地.要有效培养学生“用数学的眼光观察现实世界,用数学的思想分析现实世界,用数学的语言表达现实世界”离不开课堂上教师“有层次、有深度、可发展、能持续”的问题或问题系统激发学生的深度参与和深刻思考.有效的问题能启发学生的思维、引领学生直面知识的矛盾和冲突使思维走向深刻,从而获得良好的学习效果.但在观课中发现仍普遍存在诸如问题设置背离教学要求导致学习行为低效、过多的追问或过度细化的提问,导致学生思维断续或缺乏深层思考、未能把握有效生成适当引导阻碍学生思维走向通透等问题.课堂提问直接影响课堂效率,怎样才能使问题设置更有效?结合实践反思,可聚焦学生“需掌握什么、有什么困惑、遇什么障碍、能获得什么”四个方面.
一、需掌握什么——聚焦课程目标和知识体系
《课程标准(2011年版)》明确提出:“为使每名学生都受到良好的数学教育,数学教学不仅要使学生获得数学的知识技能,而且要把知识技能、数学思考、问题解决、情感态度四个方面目标有机结合,整体实现课程目标.”这就需要教师“总体把握数学课程的总体目标和分段目标,并在教学的每个环节都要关注目标的整体实现.”因此,准确解读课程目标要求、明确知识的纵横结构、把握教材的编写意图是问题设置的前提.
以“鸽巢原理”为例,某教研活动中教师在“探究新知”环节提出的主要问题有:
1.“如果把4支铅笔放进3个笔筒,不管怎么放,总有一个笔筒里至少有多少支笔?”
2.“如果把5支铅笔放进4个笔筒呢?把6支铅笔放进5个笔筒呢?把10支铅笔放进9个笔筒呢?把100支铅笔放进99个笔筒呢?你發现了什么?”
3.“如果把8本书放进3个抽屉,会出现怎样的结论?10本呢?”
三个问题重在让学生找出这一问题的结论是什么,但分析教材的编排(如下)不难发现,这样的问题设置实质已偏离教材的编写意图.细读教材,例题及练习为什么都以“结论+为什么”的形式而不是以“总有一个笔筒里至少有多少支铅笔”的问题形式出现?因为教学中应将重心放在验证结论的探究过程及数学模型的建构上,旨在让学生通过实物操作初步经历“数学证明”的过程,重在用“反证法”证明结论解释个中原因,并在说理过程提高学生逻辑思维能力,为后续数学证明的学习做准备.显然上述课例中以寻找答案为导向的问题设置导致教学偏离目标.
为此,对教学内容进行详尽的分析是设置有效问题的前提.聚焦学生“需掌握什么”,紧扣教学内容了解知识点对应的上位数学知识,并从中获得教学的启示;对知识点进行纵、横向的比较,从多角度把握教学内容;明确知识点在整个教材体系中的地位和作用,准确分析课程标准提出的课程目标与要求;明确知识点实质上是体现哪一方面的数学教学主题,准确把握知识的本质、教学目标与重难点.只有这样,才能准确把握问题设置的方向.
二、有什么困惑——聚焦真实起点和个体差异
在课堂实施过程中,首先要考虑学生的学习需要和能力,以学生的实际需要为教学起点设计问题.为此,课堂就新知识进行关于学生的整体情况、个体差异、真实起点、困惑点的调研是设计有效问题的关键也是不可少的环节.
以“折扣(百分数二)”为例,课前进行以下调查:
1.你知道什么是折扣吗?几折表示什么?
2.你能解决关于折扣的实际问题吗?请到商场进行调查,记录你的数学问题并尝试解答.
3.在调查的过程中,你有什么思考和疑问?
分析调查结果发现,90 % 以上的学生能比较准确表述生活中常见的简单折扣,当中约80 % 的学生知道可将简单的折扣问题转化为“求一个数的几分之几是多少”计算.在学生记录的数学问题中,出现得较多的是“已知原价和折扣,求现价”的类型.学生的疑问主要关于折扣的表示形式、折扣含义的理解和折扣的应用方面.
根据对学情的分析,在教学中重点对两大板块进行处理:
(一)加强对折扣含义的理解
教材对“折扣”含义的介绍如右图所示.在此应加强借助生活中不同的表示折扣的实例引导学生分析感悟个中含义,可提出“你是怎样理解打折的含义的?”这样的问题引导学生表述自己的看法,从而解释关于十一折、0折、十折等关于含义的疑问;通过生活情境的重现明确折扣在日常生活中的表达方式,如九折、7.5折、30 % 等,并在师生交流的过程中区分“打几折”与“减少了原价的十分之几”的不同.
(二)加强知识应用的能力
创设“已知节省的钱,求原价.”“已知现价和折扣,求原价.”“已知原价和便宜的钱,求折扣.”等实际生活问题的情境,提出“这些问题和我们学过的什么知识有关?你打算怎样解决这几个问题?”鼓励学生借助知识迁移尝试借助线段图分析,理解与百分数应用题之间数量关系的异同,并借助不同类型的变式,促进学生对“原价×折扣=现价”这个数学模型的深度理解,提高学生解决问题的能力.
从上述分析,在问题设计上应聚焦学生“有什么困惑”.思考:(1)新知识与已学知识体系中的哪些知识相关? (2)学 生的知识技能起点在哪里?在学习之前学生对该问题已有哪些思考?哪些是稍加引导就能解决,哪些需花大时间引导探究?(3)这些知识在生活中有哪些应用? (4)学 了这些知识能为学生后续哪些知识的学习做准备?
通过这样的分析能有效立足学生知识技能的真实起点,将学生最想知道和了解的问题与教学重难点有机整合,充分利用课堂的四十分钟集中解决学生的疑点、难点,促使学生的思维在不断交流碰撞中逐步走向深刻.
三、遇什么障碍——聚焦思维生成点和停滞处
学生思维水平、学习能力等因素决定学生探究新知识的过程不一定是一帆风顺的,常常会因为知识的负迁移或对新知理解得不够透彻导致思维受阻,从而产生不同的困惑,或思路已错但懵然不知.此时,就需要教师适时提出能帮助学生理清思路、引领探究的问题,让学生“拨开云雾”走向思维的深处.
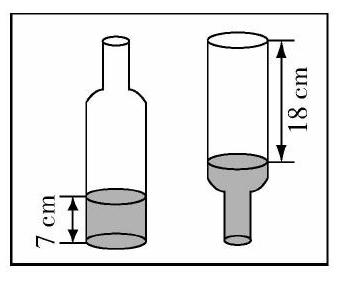
下面是“瓶子的容积”的两个教学片段.
片段一:
师:如果没有可借助的容器,有没有方法是保证瓶子完好的情况下解决这个问题呢?
生思考.
师:在思考过程中,你遇到什么困难了吗?
生1:这个瓶子不是一个完整的(规则的)圆柱,无法直接计算出容积.
师:“回想学习不规则物体的体积时,我们积累了哪些学习的经验?”
生思考并不断对水瓶观察和操作、讨论……
生2:我明白了,可以将瓶子倒置,把倒置前水的体积和倒置后空气的体积加起来,就可以求出瓶子的容积.
片段二:
师:刚才这位同学将瓶子里的水倒出一部分,把瓶子的容积转化为两个圆柱.那关于这个倒出的水的多少有讲究吗?
生:没有.
师静默.
生摆弄手上的水瓶,有的拧开瓶盖再倒水观察
……
生:“我发现倒出的水太多或太少都不行!”其他同学茫然.
师:“为什么呢?”
生:“如果倒出太少的水,水的部分就不能出现规则的圆柱;如果倒出太多的水,倒置后瓶颈部分就是不规则的图形,就不能转化了.”
“学贵在疑”.在学生不能将新知识与已有经验联系起来或没有意识到自己思考不够透彻更没有往深处思考时,教师适时地点拨至关重要.借助“回想学习不规则物体的体积时,我们积累了哪些学习的经验?”一个看似简单的提问,帮助学生打开已“积累的知识经验”的钥匙,充分利用求不规则物体体积的知识迁移解决新的问题.而利用“关于这个倒出的水的多少有讲究”直接冲击学生思维的缺陷,让学生在此处对“规则图形”有更深入的思考.通过两个关键性问题的引导促使对“转化为规则图形”及“怎样的规则图形”认识更加清晰、透彻.
为此,在问题设置上应当充分聚焦学生“遇什么障碍”.可尝试:(1)思考学生在学习过程中可能会出现的思维阻点,这些关键处应如何处理?(2)课堂上观察学生的学习行为、参与的深度和广度,并通过师生、生生对话获取学生对问题思考的掌握情况,对课堂生成的思维障碍给予关键性的引导.这样就能准确把握学生的学情即时点拨,从而促使学生往更深更广的方向思考,让思维走向通透.
四、能获得什么——聚焦问题解决策略和经验的积累
数学思考是数学教学中最有价值的行为.在学习过程中,只有经过深刻的思考才能有感悟、有反思、有质疑.但在实际课堂教学中,无效或低效问题的设置会让学生的思维零碎、浅层,导致思维仅停留在会解题上.对比“圆柱表面积计算公式”两位教师提出的问题:
课例一:
1.圆柱的表面积指的是什么?
2.你会求圆柱的表面积吗?
3.圆柱的表面是由几部分组成的?
4.怎样求圆柱底面的面积?要求圆柱的表面积就是求几个底面的面积?
5.怎样求圆柱的侧面积?把它转化为什么图形?圆柱的底面周长相当于长方形的什么?高相当于长方形的什么?
6.知道了圆柱的侧面积和底面积,怎样求表面积?
7.在计算圆柱表面积时,要注意什么?
課例二:
1.尝试画出一个长方形和两个圆形,剪下来看能否围成一个圆柱体.如果不行,请思考,怎样的长方形和圆形才能围成一个圆柱体?请尝试操作直至能围成一个圆柱体.
2.根据上述操作,你能推导出圆柱表面积的计算公式吗?请将思路写下来.
对比可见,课例一中繁、细的问题串,学生除了懂得如何计算圆柱的表面积外,并不能为后续数学学习留下什么.而课例二中,学生在操作过程中已经清晰长方形和圆形需满足怎样的条件才能围成圆柱,当学生明白到长方形与圆之间的关系,那求表面积便不是难事了.但相比课例一,这两个问题更具探究性,更能为学生后续学习积累问题解决的经验和策略.
为此,在问题的设置上,应聚焦学生能“获得什么”.避免出现知识点的分解、零碎而缺乏思考深度的问题,思考(1)除知识点外,提出的问题能否帮助学生在数学思维、探究策略方面得到发展.(2)问题的探究能帮助学生积累哪些解决问题的经验方法和策略.只有立足学生数学素养的培养方面去设计紧扣知识核心、可持续发展的问题,才能促使学生在不断探究过程中获取可持续的发展.
数学学习应该是学生主动面对问题,积极进行主体探究、推测、证明的活动.在这一学习过程中,问题是教学的核心.聚焦学生学习需要,以促进学生主动参与、深入探究为前提的问题设置能促进学生深度思考,让课堂教学真正成为学生数学素养的培养地.
