复合材料螺旋桨结构多目标优化设计

张碧辉，李喜乐，周波

(中国航天空气动力技术研究院 彩虹无人机科技有限公司，北京 100074)

0 引 言

在航空航天领域，现已广泛使用复合材料螺旋桨作为推进系统。与传统的金属螺旋桨相比，复合材料螺旋桨结构需要考虑铺层数量与铺层顺序，其设计变量数目巨大、结构复杂程度更高，相应的其可设计性也更强。

在保证结构完整性、确保桨叶强度足够的前提下，螺旋桨的结构设计应致力于减轻结构重量。周盛等[1]指出：“从桨叶上和飞机机体上减轻同等重量是不等价的，因为前者将使动负荷下降，对结构完整性、寿命和适航将有更大的裨益。”金朋等[2]、蒲鸽等[3]分别以螺旋桨重量为单一目标函数，完成了复合材料螺旋桨铺层的减重优化设计。

螺旋桨桨叶受载后的变形会导致其气动效率下降、诱发桨尖颤振、增大气动噪声及能量消耗。O.Soykasap[4]进行了螺旋桨气动剪裁优化设计，可使桨叶在受载时产生有利于提高气动效率的变形。气动剪裁技术较为复杂、实现难度较大，工程实际中多采用提高桨叶结构刚度，尤其是扭转刚度的思路，以期减小结构变形。

本文综合上述两种螺旋桨优化设计思路，以桨叶质量和桨叶扭转刚度作为优化目标函数，采用经典的多目标优化算法，得到关于两个目标函数的帕累托最优解集。

1 桨叶模型

1.1 几何模型

通常，复合材料螺旋桨桨叶多采用“蒙皮+芯材+纵梁”的剖面结构形式，梁的存在能够提高桨叶的弯曲、扭转刚度，例如直升机旋翼桨叶有“C型梁”、“D型梁”、“多腔梁”等典型剖面结构[5]，而推进螺旋桨在剖面中部也有一个或多个连接上下蒙皮的纵梁[2-3]，如图1所示。

图1 复合材料桨叶截面示意图Fig.1 Cross section of composite blade

本文选用的桨叶模型总长度为900 mm，桨叶延展向分为6段，编号1～6，桨叶内部的三根梁又将桨叶沿弦向划分为4段。上下叶面与梁共包含61个区域，桨叶的几何模型如图2所示。

图2 桨叶几何模型Fig.2 Geometry model of the blade

1.2 有限元网格

采用有限元方法对桨叶的结构响应进行计算，载荷包括气动力和惯性离心力。模型忽略了桨叶内部的泡沫芯材，使得桨叶模型的刚度减小，计算得到的位移、扭角、应变也比实际情况偏大。

有限元软件为MSC.Patran/Nastran。采用三角形三节点Paver平面单元对所有平面进行网格划分，模型被划分为2 616个单元和1 206个节点，如图3所示。

1.3 材 料

桨叶蒙皮与梁的材料均为T700碳纤维单向带预浸料(30%树脂含量)，其力学性能为：密度1.6 g/cm3(1.6×10-9t/mm3)、泊松比0.25、0°拉伸模量120 GPa、90°拉伸模量8 GPa、剪切模量4.5 GPa。

图3 桨叶网格划分Fig.3 Meshs of propeller blade

综合考虑材料的开孔、冲击损伤、湿热环境与力学性能衰退等因素，对于T700碳纤维单向带材料，其许用拉伸应变[εt]=0.003 500，许用压缩应变[εc]=0.002 700[6]。本文所用复合材料采用上述设计许用值。

1.4 属性与设计变量

规定桨叶叶面、梁的复合材料铺层沿展向为0°方向；与图1中翼型上翼面相对应的一侧为“上叶面”，另一侧为“下叶面”；靠近翼型前缘的梁为前梁，靠近后缘的梁为后梁，居中者为中梁。

根据复合材料铺层设计经验[7-8]，提高±45°铺层的比例有助于提高结构的抗剪、抗扭能力，提高0°铺层的比例有助于提高结构的抗弯能力，且90°铺层的比例不应少于10%。本文中，6个分段内各梁、各叶面的90°铺层比例为10%，±45°铺层比例和总厚度为设计变量，其中+45°与-45°铺层数相等。设计变量如表1所示，优化变量个数为33。

表1 设计变量Table 1 Design variables

1.5 约束与载荷

螺旋桨桨叶在其根部受桨榖加持，为固支约束。因此，在有限元模型中约束桨叶梁及叶面根部的平动与转动自由度，如图4所示。

图4 约束条件Fig.4 Constraint of the model

计算表明，桨叶的转动惯性力远大于气动力，故在最大转速工况下螺旋桨桨叶受载最为严酷。飞行条件为：高度H=20 km，空气密度ρ=0.088 9 m/s3，速度V=30 m/s，转速1 550 rpm；气动力合力情况为：Fx=73.19 N，Fy=0.140 1 N，Fz=0.003 46 N。

针对上述工况，在有限元模型中分别对桨叶施加：① 气动力，将气动动压数据对有限元节点位置进行插值，以2D Element Pressure的形式加载到相关单元上；② 转动离心力，对模型加载沿y轴的角速度ω=1 550 r/m=25.83 round/s。

模型加载情况如图5所示。

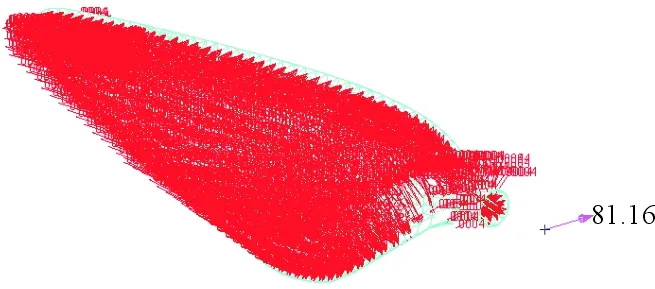
图5 模型载荷Fig.5 Load of the model

2 桨叶结构优化

由于没有可以直接量化表达桨叶刚度的指标，在本文的计算过程中，选择以桨尖挠度来表征桨叶弯曲刚度，以桨叶长度75%处扭角来表征桨叶扭转刚度。

基于第1节中建立的有限元模型，桨叶结构优化拟采取以下方案：3根梁的位置与夹角固定，以桨叶质量最小和扭角最小为优化目标，约束条件包含材料应变和桨叶挠度。优化方法为经典多目标优化算法NSGA-Ⅱ。

2.1 优化模型

(1) 设计变量

设计变量如表1所示。

(2) 目标函数

① 桨叶质量M最小。

统计图1中桨叶各区域曲面的面积，结合设计变量中铺层厚度以及材料密度，可计算得到桨叶的理论质量。本文模型中桨叶质量只包含复合材料蒙皮和梁，实际生产中桨叶质量还包含内部填充泡沫质量，该质量M′=106 g。

② 桨叶75%长度处扭角的绝对值|φ0.75|最小。

模型中75%前缘处的节点为Node580，75%后缘处的节点为Node719。桨叶变形后，两节点在y轴的位移分别为Δy580和Δy719，当地弦长为C0.75，则75%长度处的扭角值近似为

(1)

(3) 约束条件

① 弯曲刚度约束：桨尖在y轴方向的位移Δ≤5 mm；

② 拉伸强度约束：壁板材料的最大拉应变εt_max≤3.5×10-3；

③ 压缩强度约束：壁板材料的最大压应变|εc_max|≤2.7×10-3。

2.2 优化算法——帕累托最优解与NSGA-Ⅱ

在优化问题的设计空间中，满足约束条件的解称为可行解。在可行解中，如果解A的每个目标函数值均优于解B，则称解A支配解B。

某双目标函数最小化优化问题的帕累托最优解如图6所示，可以看出：在可行解中，A、B、C三点不被任何其他解所支配，该三点的解为帕累托最优解，所有的帕累托最优解构成帕累托最优解集；D、E、F三点为可行解，但其被其他解所支配，因此为非帕累托最优解。

图6 两个目标函数的帕累托分布Fig.6 Pareto front a 2-dimension function

在遗传算法中，每一代的样本数量一定，按照每个样本被其他样本所支配的数量，可以把所有可行样本分为不同等级的非支配解集。不被任何样本支配的帕累托最优解组成非支配解集F1，仅被一个其他样本所支配的样本组成非支配解集F2，以此类推。

为了增加样本的多样性，定义拥挤距离，以表征每个样本在其非支配解集中与其他样本的接近程度。

著名的多目标优化算法——快速非支配遗传算法(NSGA-Ⅱ)由K.Deb等[9]提出，其计算流程如下：

(1) 随机产生一个初始父代P0，其规模为N，在此基础上采用二元锦标赛选择、交叉和变异等操作产生子代Q0，Q0的群体规模≤N；

(2) 将Pt和Qt并入Rt中，对Rt进行快速非支配解排序，构造其所有不同等级的非支配解集F1、F2、……；

(3) 按照需要计算Fi中所有个体的拥挤距离；

(4) 构造Pt+1，首先选择支配层级高的样本，当一个层级的样本数量刚好使得Pt+1的规模超过N时，优先选择该层中拥挤距离大的样本，使Pt+1的规模刚好等于N。如图7所示[9]，F1、F2与F3中部分样本共同组成了Pt+1；

(5) 循环执行步骤(1)～步骤(4)，直至到达进化代数。

图7 新一代种群的产生Fig.7 Production of the new generation

采用Matlab编写NSGA-Ⅱ程序，通过调用有限元软件Nastran进行计算，得到桨叶位移、应变等结果，读取计算结果进行选遗传操作，经过若干轮进化迭代后，得到优化结果。参考韩庆等[10]的优化流程设计，本文的优化流程如图8所示。

图8 优化流程Fig.8 Optimization Process

2.3 优化结果

通过数值试验，确定螺旋桨结构优化问题各变量的初始值与取值范围，如表2所示。

表2 优化参数初始值与取值范围Table 2 Initial value and range of the parameters

遗传算法的种群规模M=30，进化代数T=95，优化所得帕累托最优解如图9所示，共包括19个样本点。在帕累托最优解集中选择具有代表性的两个样本点：桨叶质量最小(样本1)和桨叶扭角最小(样本19)，其设计变量优化值、目标函数值、约束条件值如表3所示。

图9 优化得到的质量、扭角双目标帕累托解Fig.9 Pareto front of blade mass and torsion angle

设计变量样本1(质量最小)样本19(扭角最小)B＿450．7500．751B＿t1/mm2．4142．401B＿t2/mm2．0782．089B＿t3/mm1．6171．618B＿t4/mm0．4200．437B＿t5/mm0．1250．125D＿450．2880．278D＿t1/mm1．5161．951D＿t2/mm0．4471．042D＿t3/mm0．4110．529D＿t4/mm0．3710．578D＿t5/mm0．3670．475D＿t6/mm0．2160．378F＿450．3280．318F＿t1/mm2．3702．416F＿t2/mm1．4191．258F＿t3/mm1．0781．213F＿t4/mm0．6751．025F＿t5/mm0．3180．684M＿450．8000．778M＿t1/mm1．8562．225M＿t2/mm1．6371．499M＿t3/mm1．2511．377M＿t4/mm1．1651．170M＿t5/mm1．0261．123M＿t6/mm0．9680．575U＿450．2000．276U＿t1/mm1．6782．029U＿t2/mm1．5101．872U＿t3/mm1．3641．980U＿t4/mm1．2021．321U＿t5/mm1．1821．234U＿t6/mm1．1320．868|ϕ0．75|/(°)0．04140M/g351409Δ/mm4．43．3εt＿max0．0006580．000679|εc＿max|1．3×10-51．1×10-5

样本1相应的桨叶位移云图、应变云图分别如图10～图13所示；上、下叶面及梁的铺层厚度云图如图14所示。

图10 样本1桨叶位移云图Fig.10 Blade displacement of sample 1

图11 样本1上叶面应变云图Fig.11 Upper surface stress of sample 1

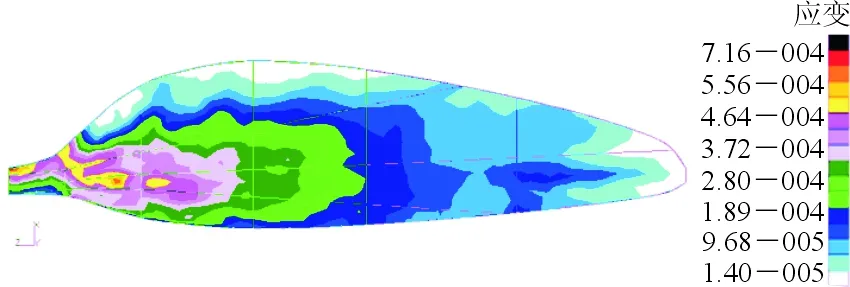
图12 样本1下叶面应变云图Fig.12 Lower surface stress of sample 1

图13 样本1梁应变云图Fig.13 Beam stress of sample 1

(a) 上叶面

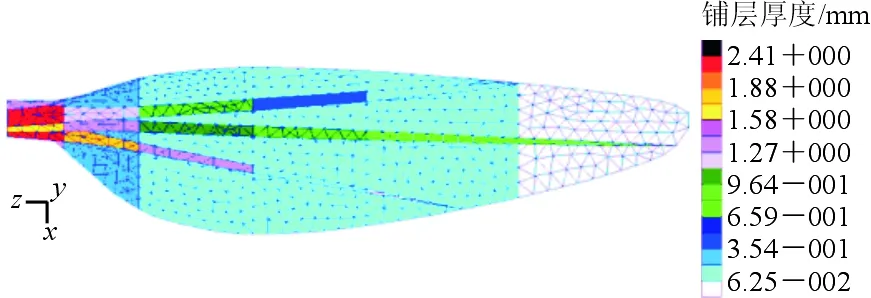
(b) 下叶面和梁图14 样本1铺层厚度云图Fig.14 Composite layup thickness of sample 1

样本19相应的桨叶位移云图、应变云图分别如图15～图18所示；上、下叶面及梁的铺层厚度云图如图19所示。

图15 样本19桨叶位移云图Fig.15 Blade displacement of sample 19

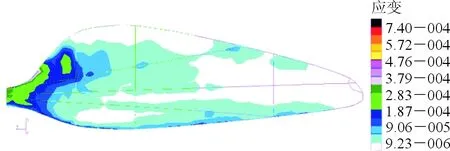
图16 样本19上叶面应变云图Fig.16 Upper surface stress of sample 19

图17 样本19下叶面应变云图Fig.17 Lower surface stress of sample 19

图18 样本19梁应变云图Fig.18 Beam stress of sample 19

(a) 上叶面

对计算结果的说明如下：

(1) 所得结果是一系列“质量”和“扭角”的非劣解，即不存在其他结果能够在质量最小和扭角最小这两个指标上同时更优；螺旋桨铺层的设计可以根据“质量”和“扭角”的重要程度，在非劣解中任选某一个；

(2) 当选择样本1时，理论上相当于忽略“扭角”目标只进行“质量”优化得到的结果，同理当选择样本19时，相当于忽略“质量”目标只进行“扭角”优化得到的结果；

(3) 所得厚度与比例均为理论值，基于优化结果进行桨叶结构设计时，应根据工艺限制对铺层作出调整：在桨叶后缘处铺层厚度不可超过理论外形；桨榖根部铺层适当过渡，不同区域、梁与蒙皮铺层适当过渡；

(4) 受限于计算硬件能力，本文优化算法中样本规模较小，得到的帕累托最优解分布较稀疏，但基于各点拟合生成的曲线应能够代表完全的帕累托最优解集。

3 结 论

本文基于快速非支配遗传算法(NSGA-Ⅱ)，在考虑螺旋桨桨叶强度、弯曲刚度约束条件下，以桨叶质量和扭角扭转刚度作为优化目标函数，得到其帕累托最优解集。最优解集中，质量最小样本的扭角为0.04 rad，质量为351 g；刚度最大样本的扭角近似为0，质量为409 g。

本文所采用的螺旋桨桨叶铺层优化设计方法对于螺旋桨结构设计具有一定的参考价值。文中仅结合最大转速工况进行分析，在桨叶设计过程中，应结合飞行器具体情况，综合考虑多种工况进行优化设计。

[1] 周盛, 顾高墀, 潘杰元, 等. 航空螺旋桨与桨扇[M]. 北京: 国防工业出版社, 1994: 55.

Zhou Sheng, Gu Gaochi, Pan Jieyuan, et al. Aeronautic propeller and prop-fan[M]. Beijing: National Defense Industry Press, 1994: 55.(in Chinese)

[2] 金朋, 钟小平, 宋笔锋, 等. 基于整数编码并行遗传算法的复合材料螺旋桨结构优化设计[J]. 机械强度, 2012, 34(2): 210-213.

Jin Peng, Zhong Xiaoping, Song Bifeng, et al. Structural optimization of composite propeller with integer-coded parallel genetic algorithm[J]. Journal of Mechanical Strength, 2012, 34(2): 210-213.(in Chinese)

[3] 蒲鸽, 宋笔锋, 安伟刚, 等. 复合材料螺旋桨结构高效优化方法研究[J]. 机械科学与技术, 2010, 29(2): 184-187.

Pu Ge, Song Bifeng, An Weigang, et al. A high-efficiency method for structural optimization of a composite propeller[J]. Mechanical Science and Technology for Aerospace Engineering, 2010, 29(2): 184-187.(in Chinese)

[4] Soykasap O. Aeroelastic optimization of a composite tilt rotor[D]. Atlanta, GA: Georgia Institute of Technology, 1999.

[5] 杨乃宾, 倪先平. 直升机复合材料结构设计[M]. 北京: 国防工业出版社, 2008: 46-48.

Yang Naibin, Ni Xianping. Composite structure design for helicopter[M]. Beijing: National Defense Industry Press, 2008: 46-48.(in Chinese)

[6] 沈真, 张晓晶. 复合材料飞机结构强度设计与验证概论[M]. 上海: 上海交通大学出版社, 2011: 25-27.

Shen Zhen, Zhang Xiaojing. An introduction to design and verification for composite aircraft structures[M]. Shanghai: Shanghai Jiaotong University Press, 2011: 25-27.(in Chinese)

[7] 牛春匀. 实用复合材料结构设计与制造[M]. 北京: 航空工业出版社, 2008: 315-368.

Niu Chunyun. Composite airframe structures[M]. Beijing: Aviation Industry Press, 2008: 315-368.(in Chinese)

[8] 中国航空研究院. 复合材料结构设计手册[M]. 北京: 航空工业出版社, 2001: 84-87.

Chinese Aeronautical Establishment. Composite structure

design handbook[M]. Beijing: Aviation Industry Press, 2001: 84-87.(in Chinese)

[9] Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197.

[10] 韩庆, 王广博, 钟小平, 等. 基于遗传算法的复合材料泡沫夹层板铺层优化设计[J]. 航空工程进展, 2013, 4(2): 182-185.

Han Qing, Wang Guangbo, Zhong Xiaoping, et al. Ply optimization design of foam sandwich composite panel based on genetic algorithm[J]. Advances in Aeronautical Science and Engineering, 2013, 4(2): 182-185.(in Chinese)