基于人机闭环稳定性的舵机速率限制边界

刘艳，高正红，张星雨

(西北工业大学 航空学院，西安 710072)

0 引 言

飞机的人机耦合(Aircraft Pilot Coupling，简称APC)现象，是由非正常的飞机与驾驶员动力学特性相互影响，使得人机系统闭环失稳而产生的持续、不可控、严重威胁飞行安全的振荡或发散现象[1]。

现代飞机普遍采用了电传操纵系统，其操纵面由舵机驱动偏转。舵机的偏转速率取决于其功率，当偏转指令超出舵机偏转能力时，就会产生舵机速率限制。对于广泛采用主动控制与放宽静稳定性技术的现代飞机来说，操纵面尺寸更小，舵机偏转压力更大，舵机速率限制问题尤为突出[2]。

舵机速率限制非线性会带来可观的相位滞后与幅值衰减[3]，是现代电传飞机发生APC的主要诱因，几乎所有的电传操纵飞机，包括F-16、F-18、JAS-39、F-22、C-17、B-2、A-320等，都发生过由舵机速率限制造成的严重APC事件[1,4]。

舵机偏转速率取决于其功率，因此避免由此发生APC的最直接方法是提高舵机功率，但这也意味着技术难度、研制成本及重量的增加，为总体设计阶段的舵机选型带来了困难，亟需一种确定人机闭环系统稳定所需最小舵机偏转速率的方法，以最小的代价避免APC的发生、提高研制效率。

国内外针对由舵机速率限制诱发的Ⅱ类PIO已开展了大量研究，包括影响机理[1,5]、评估准则[3,6]、抑制方法[7-8]及人机闭环稳定域[9]等，但尚无公开文献明确给出适合总体设计阶段确定舵机速率边界的方法。开环起始点(Open Loop Onset Point，简称OLOP)准则[3]与Neal-Smith时域(Time Domain Neal-Smith，简称TDNS)准则[6]均可通过评估不同舵机速率下的APC/PIO趋势试凑出人机闭环稳定所需的最小舵机速率；但OLOP方法使用的是纯增益驾驶员模型，不能充分体现驾驶员的操纵特性；TDNS方法使用的虽是最优McRuer驾驶员模型，但存在计算量大、局部最优解与阈值选取问题。

本文基于描述函数分析舵机速率限制非线性对人机闭环系统稳定性的影响规律，建立舵机速率限制边界的确定方法，并通过OLOP准则对所建立的方法进行验证。

1 非线性舵机模型

1.1 舵机模型

典型舵回路如图1所示，由舵机、放大器及反馈元件组成[10]。

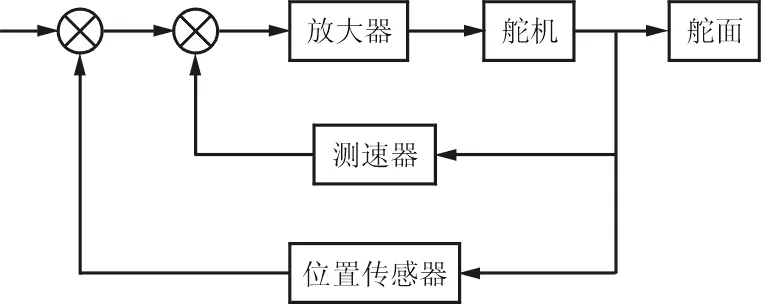
图1 舵回路示意图Fig.1 Schematic of actuator circuit

舵面偏转速率由测速器测量并反馈给放大器以增加舵回路的阻尼；舵机偏转角度则由位置传感器测量并反馈到输入端，以保证精确控制舵机偏角。因此舵回路特性可用典型二阶振荡环节表示，由于其固有频率远高于飞机的带宽，可近似用一阶惯性环节表示：

(1)

简化的舵机模型可用带速率限制的一阶惯性环节描述[3,11]，如图2所示。图中，δc为舵机偏转指令信号；δ为偏转输出信号；e为误差信号；ωa为舵机带宽；VL为速率限制；eL=VL/ωa为饱和点。

图2 简化的舵机模型Fig.2 Simplified actuator model

1.2 非线性描述函数

如果非线性元件的输入是正弦信号，其输出通常未按照正弦变化，但是与输入信号周期相同的周期函数。按照傅里叶级数概念，输出信号可分解为与输入信号相同频率的一次谐波和n次谐波。

在工程实际中，非线性元件输出信号的高次谐波分量幅值通常远小于一次谐波，加之大部分控制元件都是低通滤波器，因此可以用输出信号的一次谐波分量来近似此元件的输出特性，即所谓的描述函数[10]。

假设非线性元件的输入信号按照正弦变化：

x(t)=Xsinωt

(2)

则输出信号可分解为与输入信号相同频率的一次谐波与n倍频率高次谐波之和：

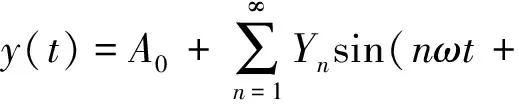
(3)

y1=A1cosωt+B1sinωt

(4)

式中：y1为输出信号的一次谐波分量。

其一次谐波分量即为此元件的描述函数：

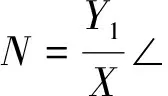
(5)

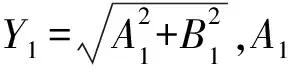
1.3 速率限制非线性的描述函数

速率限制的输入与输出特性如图3所示，如果输入为正弦波，其输出则接近三角波。

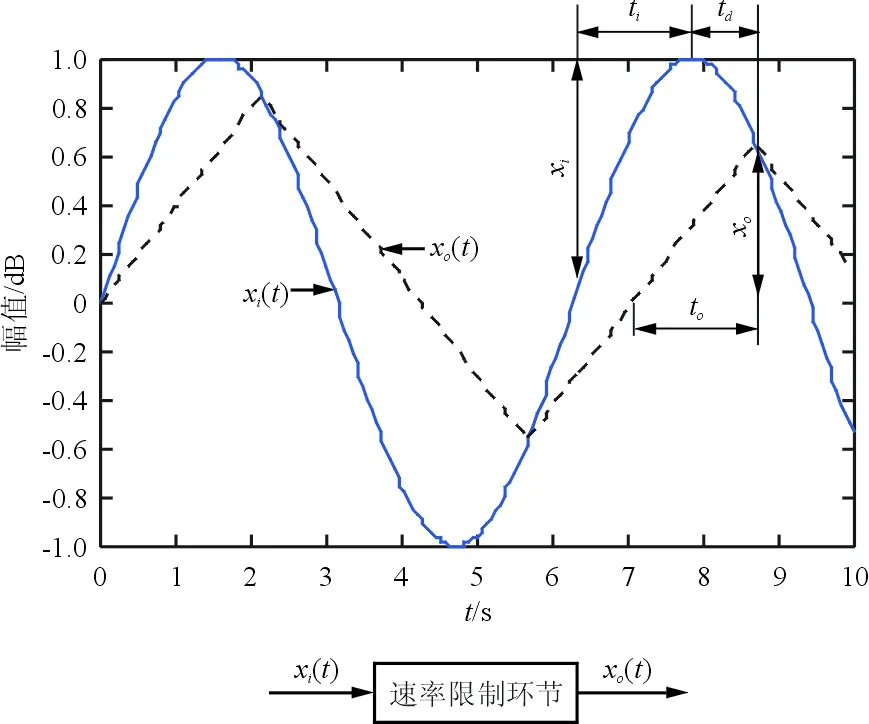
图3 速率限制的输入与输出特性Fig.3 Input and output of rate limiting

假设速率限制非线性的正弦输入为

xi(t)=xisinωt

(6)

根据文献[3,12]中的推导过程可得到速率限制的描述函数：

(7)

式中：VL为舵机速率限制值；A为输入信号幅值；ωonset=VL/A为发生频率。

该描述函数是基于正弦输入/三角输出假设得到，故仅适用于舵机速率完全饱和的情况，即ω>1.862ωonset[12]；ω<ωonset时，舵机速率未发生饱和；ωonset<ω<1.862ωonset时，舵机速率未完全饱和，无法使用式(7)中的描述函数，可采用以下经验公式确定速率限制环节的幅值与相位[12]：

(8)

式中：x=ω/ωonset，x∈[1,1.862]。

ωonset=1时速率限制描述函数的bode图如图4所示。

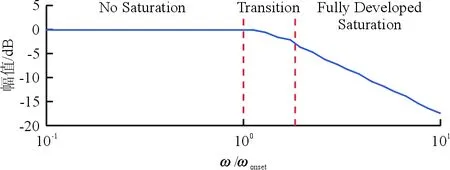
(a) 幅值图

(b) 相位图图4 舵机速率限制的Bode图Fig.4 Bode plot of actuator rate limiting

从图4可以看出：当系统频率ω<ωonset时，未发生速率限制，系统的幅值与相位未发生变化；当ωonset<ω<1.862ωonset时，速率限制开始发生但未完全饱和，幅值相位均有小幅下降；当ω>1.862ωonset时，舵机速率完全饱和，幅值与相位均显著下降。

在飞机正常频率范围(1.5～3.5 rad/s)内，舵机速率限制带来的相位滞后最大可达60°～80°，导致系统的相位裕度减小，甚至不稳定。

2 速率限制边界

2.1 非线性稳定准则

带舵机速率限制非线性的人机闭环系统如图5所示。

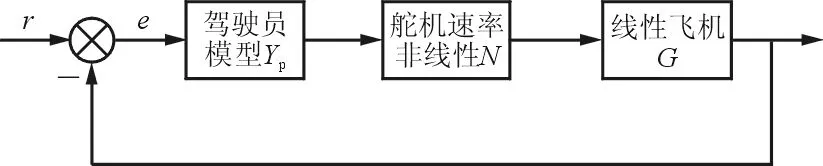
图5 非线性人机闭环系统示意图Fig.5 Closed-loop PVS with nonlinear element

其特征方程为

1+YpNG(s)=0

(9)

假设舵机速率非线性的描述函数为N(A,ω)，飞机线性部分传递函数为G(jω)，驾驶员模型传递函数为Yp(jω)，则闭环系统发生持续振荡的条件为

1+Yp(jω)N(A,ω)G(jω)=0

(10)

或

(11)

将线性Nyquist判据[13]扩展到非线性，可利用G(jω)Yp(jω)与-1/N(A,ω)曲线的相对位置关系判断非线性系统的稳定性，即所谓的负倒描述函数法：

(1) 如果-1/N(A,ω)曲线没有被G(jω)·Yp(jω)曲线包围，如图6所示，则系统稳定。

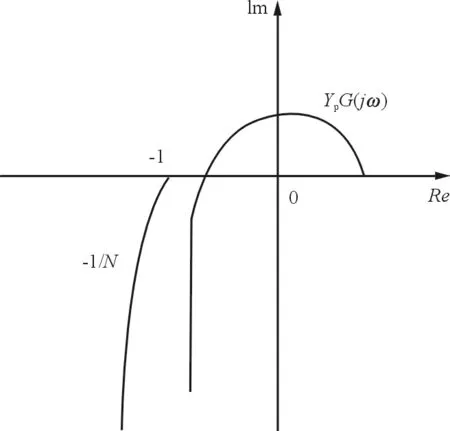
图6 稳定系统的Nyquist图Fig.6 Nyquist chart of a stable system

(2) 如果-1/N(A,ω)曲线被G(jω)Yp(jω)曲线包围，如图7所示，则系统不稳定。

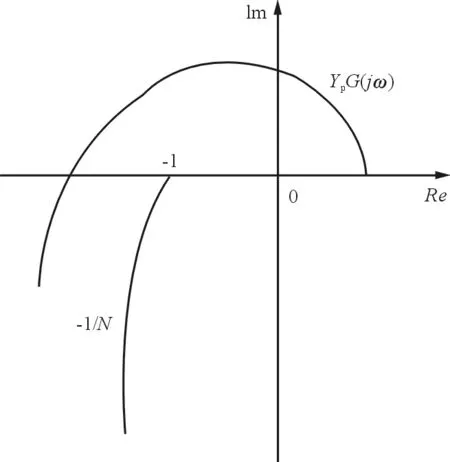
图7 不稳定系统的Nyquist图Fig.7 Nyquist chart of an unstable system

(3) 如果两曲线相交，如图8所示，则系统会出现持续振荡；二者交点即为闭环振荡对应的ω/ωonset。

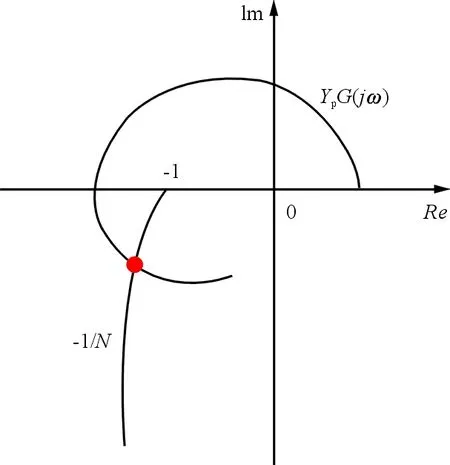
图8 振荡系统的Nyquist图Fig.8 Nyquist chart of an oscillatory system

根据式(7)可以绘制舵机速率限制非线性的负倒描述函数，如图9所示。

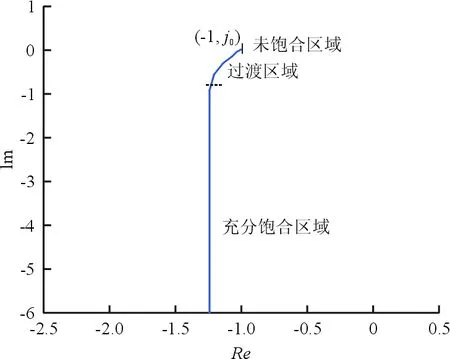
图9 速率限制的负倒描述函数Nyquist图Fig.9 Nyquist Chart of -1/N of rate limiting

从图9可以看出：当ω<ωonset时，舵机未发生速率限制，描述函数幅值为1，相位为0，其负倒描述函数的Nyquist坐标为(-1,j0)；随着ω的增加，尤其是ω>1.862ωonset后，其负倒描述函数的幅值与相位均增加，相应的Nyquist坐标向左下方移动。ωonset越高，发生速率限制及与线性部分相交所对应的ω越高，闭环系统越不容易失稳。

2.2 驾驶员模型

本文使用的驾驶员模型为McRuer模型[5]

(12)

式中：Kp为驾驶员模型的增益；τp为驾驶员时间延迟，通常取为0.15～0.25 s；TL和TI为驾驶员提供的超前与滞后补偿时间。

由于驾驶员的自适应特性，操纵增益与补偿时间均随具体飞行任务与飞行状态变化，因此要确定舵机速率非线性边界，应首先确定该状态下的驾驶员模型参数。

本文将参考TDNS准则[6]，以图10所示闭环姿态操纵任务最小误差均方根(Root Mean Square，简称RMS)对应的Kp与Tc为最优驾驶员参数。其中，θc为俯仰操纵指令；D为目标捕获时间，D越小表明驾驶员达到期望响应的时间越短，任务要求越高，应根据飞机的任务类型及飞行状态选取。

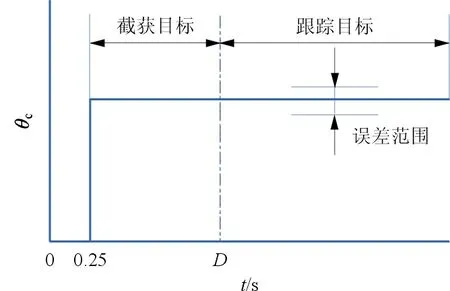
图10 TDNS准则的阶跃目标跟踪任务Fig.10 Step target tracking task of TDNS criterion

Tc为驾驶员提供的补偿时间，当Tc>0时，为超前补偿，如式(13)所示；当Tc<0时，为超前-滞后补偿，如式(14)所示。

(13)

(14)

式中：ωBW为任务带宽。

(15)

响应的RMS反映了闭环系统的振荡特性，RMS越大表明闭环响应振荡越激烈。Kp与Tc可采用序列二次规划(Sequencial Quadratic Programming，简称SQP)方法确定[14]。

2.3 速率限制非线性稳定边界

根据负倒描述函数法，如果-1/N(A,ω)曲线与G(jω)Yp(jω)曲线相交，其交点即为闭环振荡对应的ω/ωonset。若飞机的操纵带宽ωac已知，则可确定人机闭环稳定所对应的最小ωonset：

(16)

由ωonset=VL/A可知，闭环系统稳定所需的最小舵机偏转速率VLmin与最小发生频率ωonset_min相对应。因此，在确定ωonset_min后，可根据操纵面的偏转范围A确定保证闭环稳定的最小舵机速率：

VLmin=ωonset_min·A

(17)

操纵面偏转范围A对应的是极限操纵状况，故由此确定的最小舵机速率可以保证最极限操纵任务下的闭环稳定性。

3 算例与验证分析

3.1 算例飞机简介

以某放宽静稳定飞机的俯仰通道为例，对所提出的速率限制边界确定方法进行验证，算例状态为H=5 km，Ma=0.75。

该状态下飞机本体的短周期状态方程为

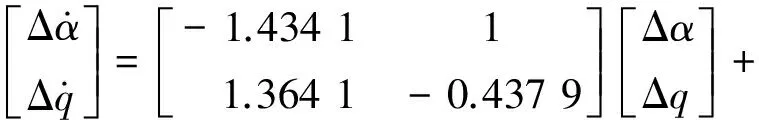
(18)

其短周期特征根为(-2.205 7，0.333 7)，为了获得期望的短周期阻尼比ζsp与频率ωsp，本文为其设计过载指令式积分控制增稳系统，如图11所示。

算例状态下的增益分别为Kq=0.145，Kα=0.41，Kp=0.36，KI=1.2。通过等效系统拟配可以得到增稳后的ζsp为0.697 3，ωsp为2.734 4，满足一级飞行品质要求。根据带宽准则[2]，可以确定“飞机+飞控系统”的纵向带宽ωac=3.058 8。

由于飞机本体纵向不稳定，舵机一旦发生速率限制，由俯仰操纵面提供的增稳效果将减弱甚至消失，导致严重APC的发生。

3.2 俯仰操纵面舵机速率边界

本文用于确定驾驶员模型参数的目标跟踪时间D取为1.4 s，驾驶员模型的时间延迟项τp取为0.2 s，根据文献[14]中的方法可以得到驾驶员模型参数为Kp=2.03，TL=0.15 s，TI=0。由此可以得到俯仰通道的Nyquist图(如图12所示)，-1/N(A,ω)曲线与G(jω)Yp(jω)曲线交点对应的ω/ωonset为2.255 1。

闭环稳定所需要的最小ωonset

由俯仰操纵面的最大偏转角A=20°可以得到

VLmin=1.356×20=27.1°/s

3.3 OLOP准则验证

不同舵机速率下，采用文献[3]中方法确定的该飞机OLOP准则评估结果如图13所示。

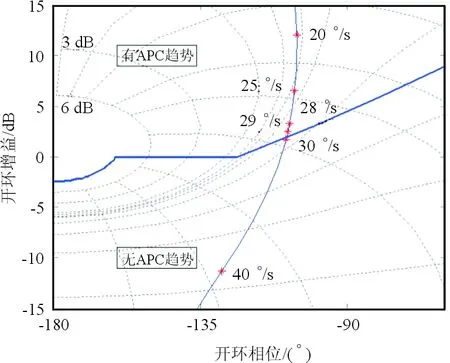
图13 不同舵机速率下的OLOPFig.13 OLOP of different actuator rate limiting

从图13可以看出：当舵机速率较小时，算例飞机的OLOP位于边界之上，速率饱和产生的相位滞后会引起闭环幅值的显著增大，从而激发出更强的速率饱和，导致相位滞后的进一步增加，最终导致闭环失稳；随着舵机速率的增加，算例飞机的OLOP呈向下方移动趋势，此时相位滞后增加所导致的闭环幅值的增幅逐渐减小，系统的闭环稳定性逐渐增加。

系统的Nichols曲线与OLOP准则稳定边界交点所对应的舵机速率，即舵机速率边界为29～30 °/s，与本文所建立方法确定的27.1 °/s极为接近。

造成二者误差的主要原因是：OLOP准则使用的模型为纯增益模型；本文所建立方法使用的是包含最优驾驶员增益、超前补偿和时间延迟的McRuer模型。最优增益与超前补偿均可以提高闭环系统稳定性，时间延迟项则会一定程度降低系统稳定性；在三者共同作用下，使用McRuer模型的人机闭环系统比使用纯增益模型更稳定，因此所确定的最小舵机速率略小于OLOP准则确定的结果。

4 结 论

(1) 本文提出的舵机速率边界的确定方法最小成本的避免了人机耦合。该方法确定的舵机速率与OLOP边界对应的舵机速率极为接近，OLOP准则的结果略高于所确定的限制边界。

(2) 本文所提出的方法可为总体设计阶段的舵机选型提供参考，在实际使用时还应充分考虑不同飞行任务、状态及飞机构型带来的影响。

(3) 不同设计阶段由于可获得的数据详细程度不同，所面临的APC/PIO问题也不尽相同，在后续的详细设计、原型机试制与试飞阶段，可能会不断出现新的APC/PIO问题，还需开展相应的准则与试飞评估、抑制甚至实时探测研究。

[1] Committee on the Effects of Aircraft-pilot Coupling on Flight Safety. Aviation safety and pilot control[M]. Washington: National Academy Press, 1997: 14-15.

[2] David G Mitchell, Roger H Hoh, Bimal L Aponso. Proposed incorporation of mission-oriented flying qualities into MIL-STD-1797A[R]. WL-TR-94-3162, 1994: 67-68.

[3] Holger Duda. Prediction of pilot-in-the-loop oscillations due to rate saturation[J]. Journal of Guidance, Control, and Dynamics, 1997, 20(3): 581-585.

[4] David Mitchell, David Klyde.Testing for pilot induced oscillation[C]. AIAA-2005-5811, 2005.

[5] 高金源, 李陆豫, 冯亚昌. 飞机飞行品质[M]. 北京: 国防工业出版社, 2003: 262-267.

Gao Jinyuan, Li Luyu, Feng Yachang. Airplane flight dynamics[M]. Beijing: National Defense Technology Press, 2003: 262-267.(in Chinese)

[6] Randall E Bailey, Timothy J Bidlack. A quantitative criterion for pilot-induced oscillations-Time domain Neal-Smith criterion[C]. AIAA-96-3434, 1996.

[7] Donald A Johnson. Suppression of pilot-induced oscillation[D]. USA: Air Force Institute of Technology, 2002.

[8] Lars Rundaqwist, Robert Hillgren. Phase compensation of rate limiters in JAS 39 Gripen[C]. AIAA-96-3368, 1996.

[9] 曹启蒙, 李颖晖, 徐浩军. 考虑作动器速率饱和的人机闭环系统稳定域[J]. 北京航空航天大学学报, 2013, 39(2): 215-219.

Cao Qimeng, Li Yinghui, Xu Haojun. Stability region for closed-loop pilot-vehicle system with actuator rate saturation[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(2): 215-219.(in Chinese)

[10] 高浩, 朱培申, 高正红. 高等飞行动力学[M]. 北京: 国防工业出版社, 2004: 182-185.

Gao Hao, Zhu Peishen, Gao Zhenghong: Advanced flight dynamics[M]. Beijing: National Defense Technology Pr-ess, 2004: 182-185.(in Chinese)

[11] 孟捷, 徐浩军, 刘东亮. 基于描述函数法的速率限制环节特性研究[J]. 飞行力学, 2009, 27(3): 20-23.

Meng Jie, Xu Haojun, Liu Dongliang. Research on the characteristic of rate limiting element based on describing function method[J]. Flight Dynamics, 2009, 27(3): 20-23.(in Chinese)

[12] Joel B Witte. An investigation relating longitudinal pilot-induced oscillation tendency rating to describing function predictions for rate-limited actuators[D]. USA: Air Force Institute of Technology, 2004.

[13] Katsuhiko Ogata. Modern control engineering[M]. 5th ed. USA: Prentice Hall, 2010: 440-467.

[14] 赵志忠, 刘艳, 高正红. 基于序列二次规划的PIO易感性时域评估方法[J]. 飞行力学, 2010, 28(4): 1-4.

Zhao Zhizhong, Liu Yan, Gao Zhenghong. PIO susceptibility evaluation approach based on sequential quadratic programming[J]. Flight Dynamics, 2010, 28(4): 1-4.(in Chinese)