基于贝叶斯网络的空战效能评估方法研究
2018-02-03汪泽辉方洋旺
汪泽辉,方洋旺
(空军工程大学 航空航天工程学院,西安 710038)
0 引 言
传统的空战效能评估方法包括:ADC评估方法、决策树模型评估方法、层次分析法、专家方法、作战效能仿真评估方法等[1]。评估工作最重要的作用是能够对结果做出解释,并辅助人员进行决策。
空战过程是一个极为复杂的过程,具有较高的不确定性[2],战场上繁多的不确定因素会给评估结果带来较大误差。贝叶斯网络以图形网络的形式非常直观地给出了事物之间的联系,既综合了专家先验知识,又对仿真数据所蕴含的信息进行了充分发掘;同时,贝叶斯网络本身具有强大的推理能力,可以推理出产生某种问题的原因或者推理出某些原因可能造成的结果,提高了评估的有效性和可靠性。目前,贝叶斯网络已用于数据分析[3-4],评估毁伤[5-7]、可靠性[8]、作战效能[9]等方面。周兴旺等[10]提出了一种BP神经化的贝叶斯网络模型用于评估目标毁伤,王巍[11]提出了一种基于云参数贝叶斯网络的威胁评估方法,David Barber[12]介绍了贝叶斯网络在人工智能领域的最新发展与应用。
本文对整个空战过程进行分析,建立基于贝叶斯网络的空战效能评估模型,确定评估指标,并给出仿真实例以验证模型的有效性与准确性。
1 先验贝叶斯网络效能评估模型的构建
贝叶斯网络是由网络结构G与网络参数θ构成的有向无圈图,即B=
利用贝叶斯网络进行效能评估的工作流程如图1所示,其主要步骤为:①根据专家知识建立先验贝叶斯网络;②建立仿真模型获取仿真实验数据;③通过网络学习确定后验网络;④依据后验网络进行作战效能评估分析。
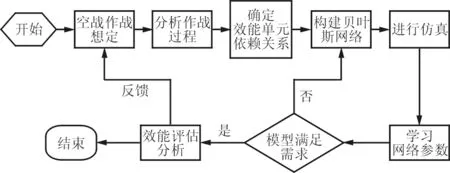
图1 贝叶斯效能评估流程图Fig.1 Flow chart of Bayesian effectiveness evaluation
本文将基于贝叶斯网络的空战效能评估网络进行模块化划分,分为信息优势评估模块、决策指挥能力评估模块、协同能力评估模块和部队效能评估模块四个子模块。该模块划分方法可有效减少网络学习的复杂性,提高学习效率。
1.1 确定贝叶斯网络节点分类
在应用贝叶斯网络对空战效能进行评估的过程中,根据对空战过程的分析,可将影响空战效能的各不确定因素根据不同的物理意义,分为以下节点[14-16]。
(1) 作战想定节点
作战想定节点用于描述作战想定方案,包括导弹数量(MN)和发射平台(LP)。
(2) 扰动因素节点
扰动因素节点是在战场环境中的不确定因素节点,包括态势感知能力(RDC,由发现能力(FC)、识别能力(RC)和跟踪能力(TB)共同决定),抗干扰能力(ATC),数据链性能(DT)。
(3) 中间因素节点
中间因素节点用来描述受到作战想定、目标信息或者扰动因素等影响,从而影响最终仿真评估结果的不确定性事件或者过程,包括协同探测能力(CRS),协同制导能力(CMG),协同目标分配能力(CTA),导弹性能(MP,由导弹的发射能力(LC)、制导能力(MC)和命中概率(HP)决定),毁伤效能(DE),导弹作战能力(MK),红方作战单元的生存能力(SC)。
(4) 目标信息节点
目标信息节点用来描述蓝方的不确定信息,包括目标的易损性(TD)和目标导弹攻击能力(TMK)。
(5) 评估目标节点
评估目标节点是描述最终评估问题及评价结果的因素,包括信息优势(IP),协同能力(CC),决策指挥能力(DCC),部队效能(ME)以及整体的作战效能(CE)。
贝叶斯效能评估网络模块如图2所示。
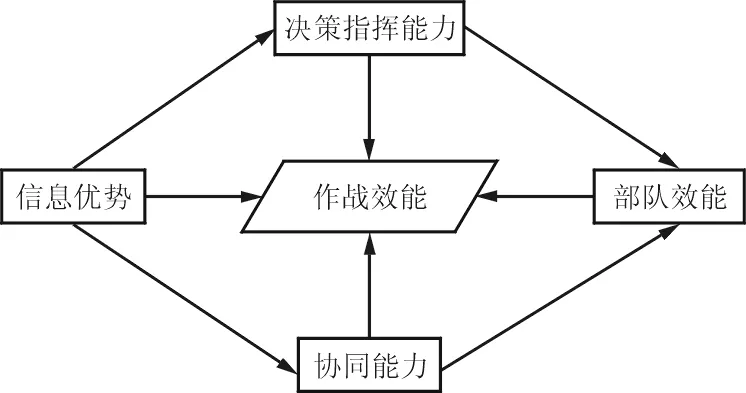
(a) 整体效能评估模块
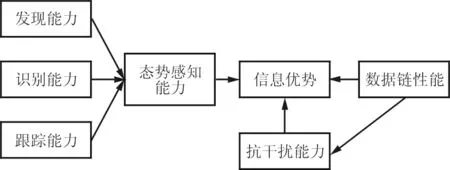
(b) 信息优势模块
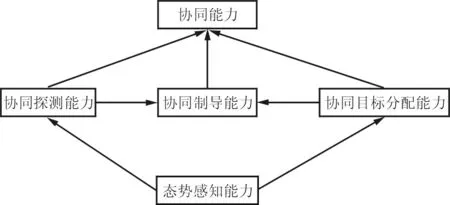
(c) 协同能力模块
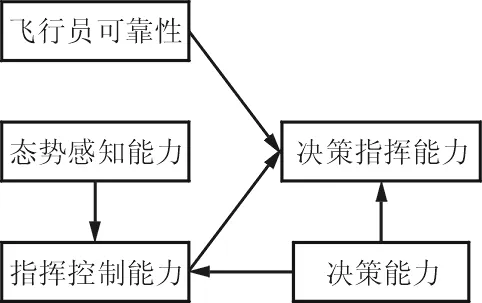
(d) 决策指挥能力模块
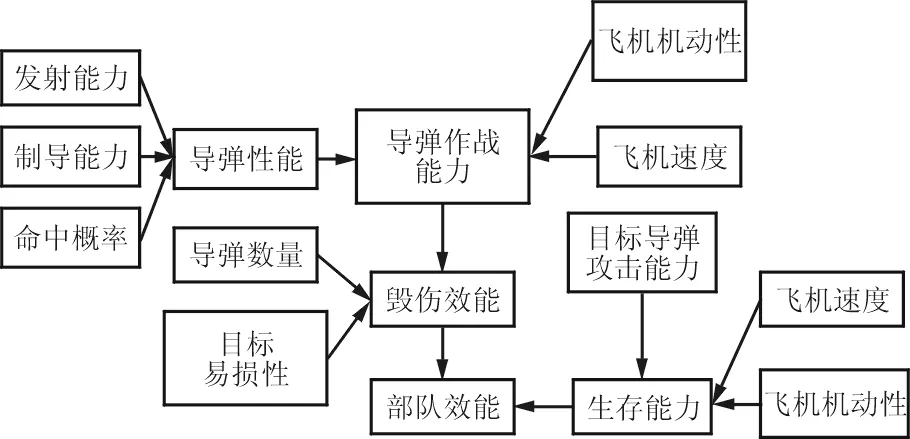
(e) 部队效能模块图2 贝叶斯效能评估网络模块Fig.2 Bayesian effectiveness evaluation network module
1.2 网络节点的模糊评判
上述评估空战效能的贝叶斯网络节点,其中部分节点状态变量离散,例如,导弹数量(MN)节点的分布一般为均匀分布。但大部分节点均为定性表述,例如抗干扰能力的优劣、毁伤能力的高低等。通常采用专家打分法,即专家根据知识对相应取值节点进行对应的划分。例如,毁伤能力值β,当β∈[0,0.3)时,表示毁伤能力差,当β∈[0.3,0.6)时,表示毁伤能力为中等,当β∈[0.6,1.0)时,表示毁伤能力强。但是这种绝对的区间划分无法体现出当定性语言转化为定量表达时的不确定性与模糊性。如何将定性的描述转换为定量的评价,同时又保留定性描述的模糊性与随机性,是必须解决的问题。本文采用云模型表征定性结果的随机性与模糊性,并在评价过程中,通过改进评价范围的划分来避免分界太绝对的问题。
对于人为定义的定性概念,其隶属云的期望曲线近似服从正态分布或半正态分布。因此,可用正态云来表达定性语言值,其数学期望曲线为
MECA(x)=exp[-(x-Ex)2/(2En)2]
(1)
基于云模型的综合评判数学模型,用于对专家给的先验知识进行划分,步骤如下:
(1) 由m种判断构成评价集,记为V={v1,v2,…,vm}。一般为优、中、差等类似的语言集,每个语言集对应相应的评价云模型,云模型的确定是由专家给出相应评语对应的分数区间[Bmin,Bmax],利用式(2)计算得到云模型的参数。
(2)
式中:k为常数,可根据实际情况确定。
(2) 将所给参数(Ex,En,He)生成云模型,μ(x)表示隶属度,记为(x,μ(x))。
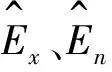
假定专家给出了区间[0.3,0.6),[0.35,0.65),[0.4,0.7),根据上述步骤生成云模型,再由逆向云算法生成模糊评判数学模型,区间评定结果为[0.38,0.62),如图3所示。
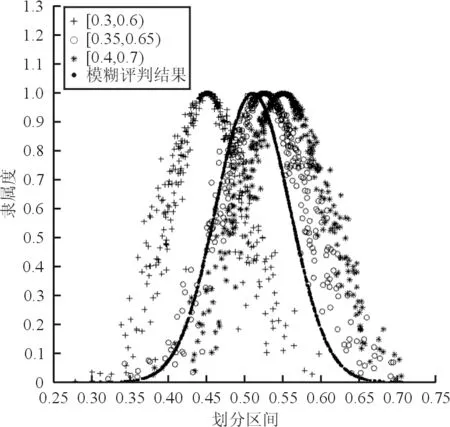
图3 模糊评判云模型Fig.3 Fuzzy judgment cloud model
2 后验贝叶斯网络效能评估模型的构建
传统的评估网络是由相关领域的专家根据事物之间的关系确定结构模型,再用其他方法确定节点参数。但该方法无法保证其客观性、可靠性。为了保证评估网络拓扑结构的客观与可靠,最优方法是将观测数据与专家知识相结合,共同构建评估网络[17-18]。限于篇幅,以部队效能模块为例进行说明。以下学习算法的数据均来自空战模拟仿真系统,经过预处理,得到用于学习算法的数据集。
2.1 结构学习
所采用的结构学习算法为K2搜索算法,该算法基于BDe测度,结合爬山搜索策略,其思想是从一个空网络开始,将专家给出的节点顺序作为先验,逐步为节点添加使其后验概率最高(评分最高)的节点作为该节点的父节点,并依次遍历完所有父节点。与其他结构学习方法相比,来自专家的先验知识可以有效缩小网络学习过程中的搜索空间。本文选择基于计分的方法,确定一个测度函数,根据事先确定的节点顺序,选择使后验结构概率最大的节点作为该节点的父节点,依次遍历所有的节点,逐步为每一个变量添加最佳的父节点。
测度函数定义为
scroe(Xi,Pa)
(3)
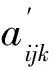
算法的具体流程为
输入:节点顺序ρ,每个节点最大父节点的个数u,数据集D。
输出:最优网络结构G。
G=φ
forj=1 ton
π(Xi)=φ
Vold=score(
While(ture)
i=arg max1≤i≤jscore
Vnew=score
if (Vnew>Voldandπ(Xj))
Vold=Vnewπ(Xi)=φ
π(Xj)=π(Xj)∪Xi
G=G∪{Xi→Xj}
end
else break
end
end
先验网络结构如图4所示。
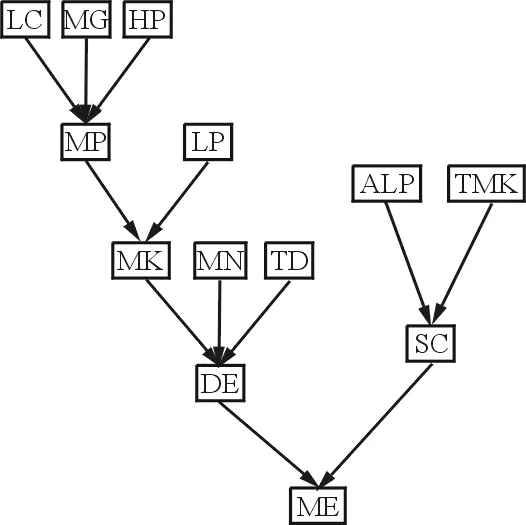
图4 先验贝叶斯网络结构Fig.4 Priori Bayesian networks structure
采用打分方法进行4次网络结构学习,每次学习增加300个样本,得到后验贝叶斯网络结构,如图5所示。
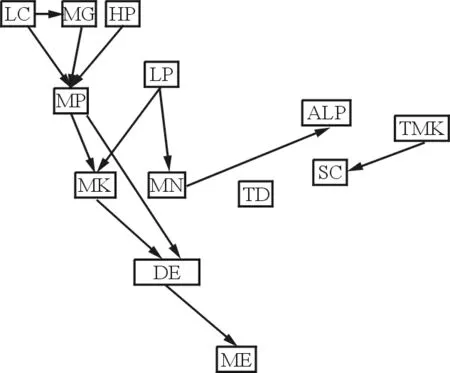
(a) 第一次结构学习结果
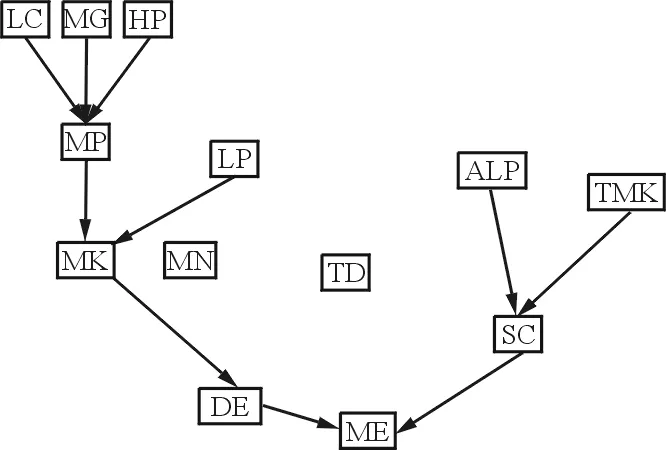
(b) 第二次结构学习结果
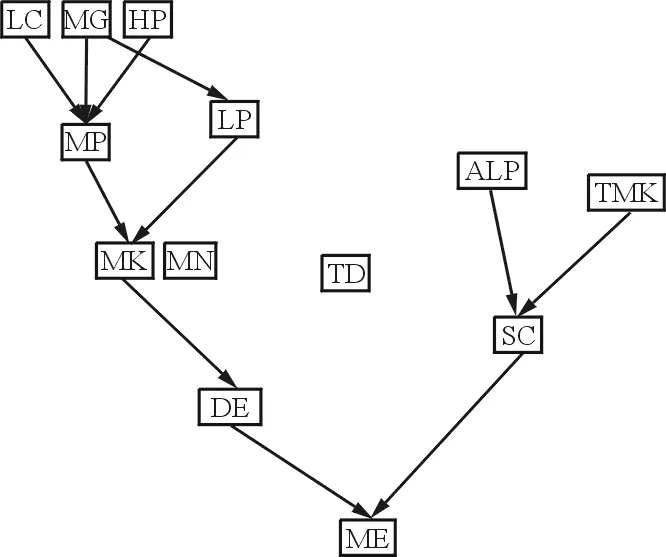
(c) 第三次结构学习结果
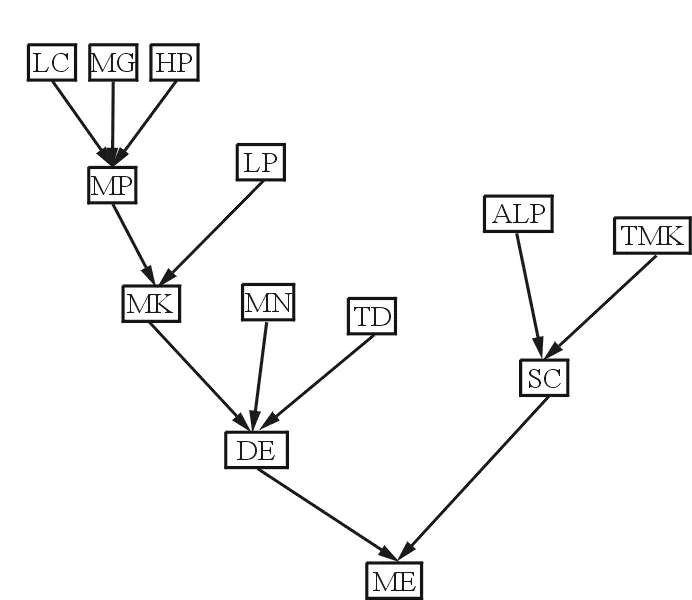
(d) 第四次结构学习结果图5 后验贝叶斯网络结构Fig.5 Posterior Bayesian networks structure
从图5可以看出:经过第一次学习的后验贝叶斯网络并不能明显地观察到节点之间的相互联系;随着学习样本的增加,网络结构出现了明显变化,网络结构逐渐趋于稳定,只是在局部出现了增添边,节点之间相互影响的关系趋于明显;在经过第四次结构学习之后,样本数量达到一定规模,贝叶斯网络结构与先验一致,验证了先验网络的合理性。
2.2 参数学习
参数学习是从仿真数据中获取后验贝叶斯网络模型的CPT的过程,其直接影响着网络推理的速度和精度,更新网络变量原有的先验分布是贝叶斯网络学习的重点和难点。采用MLE估计算法,其主要思想是寻找使得似然函数最大的参数,通过给定父节点集的值,计算节点取不同值的概率,并作为节点的条件概率参数。假设网络中的参数是离散的且服从Dirichlet分布,给定观测数据集D={Y1,Y2,…,YN},则数据集的似然函数模型参数为
(4)
或等价使用对数似然,即
(5)
对数似然函数中的每一项可以进一步分解:
(6)
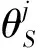
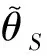
(7)
根据专家知识,确定网络节点的先验分布,即参数学习所需的先验知识,以ME节点为例,其先验分布如表1所示。节点的取值范围为{能力差,能力中等,能力好},用{1, 2, 3}来表示。
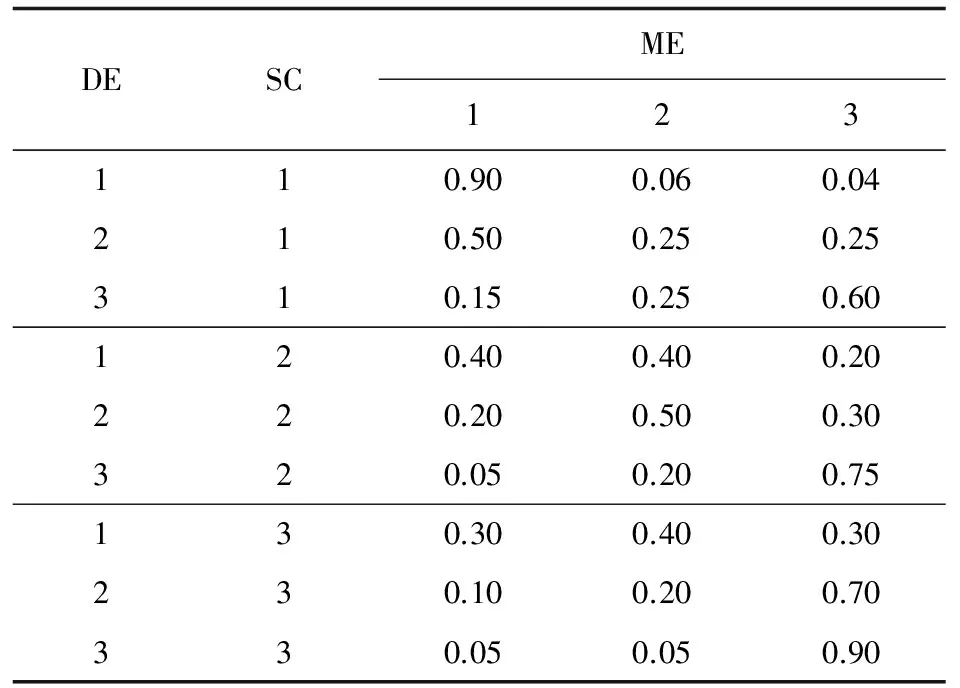
表1 节点ME的先验分布Table 1 Prior distribution of ME
经过学习,可以得到部队效能评估贝叶斯网络模型中ME节点的CPT,如表2所示。
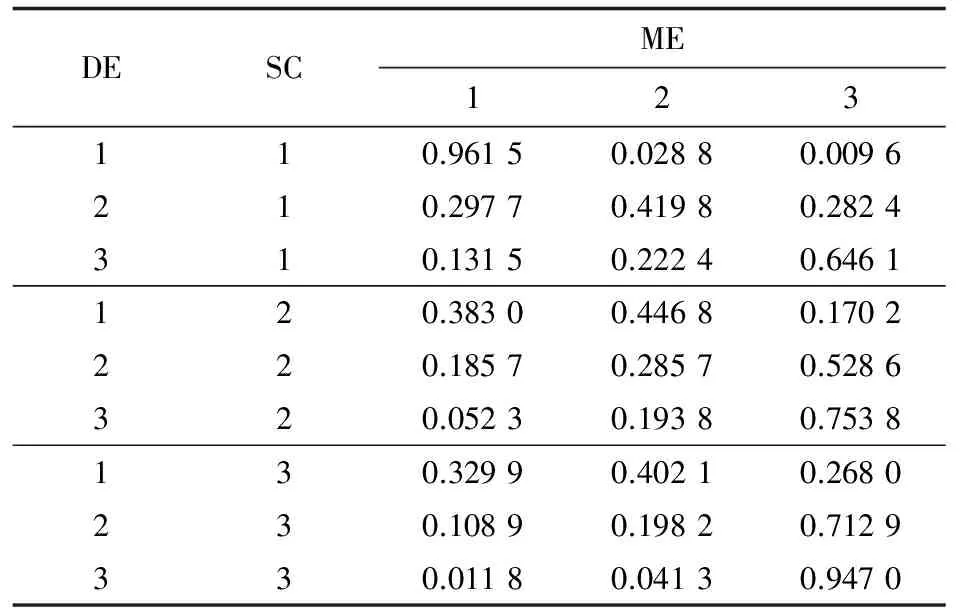
表2 参数学习后节点ME的CPTTable 2 CPT of ME with parameter learning
3 基于Bayesian networks评估模型的空战效能评估分析
在建立了基于贝叶斯网络的空战效能评估模型之后,便可以采用贝叶斯网络推理方法对作战效能以及影响因素进行推理。贝叶斯网络节点间的独立性使得精确推理算法具有可实现性,并且节点间独立性越强的网络,其推理计算效率越高。采用基于联接树(Junction Tree,简称JT)的贝叶斯网络推理算法——Hugin推理,该算法是目前推理速度最快的精确推理算法,不仅适用于单连通的网络,还能完成对多查询节点的多连通网络推理计算。Hugin推理算法的主要思想是先将贝叶斯网络图中的节点转化为节点图,定义信息传递过程,推理在相邻的节点图中进行,进而完成推理计算。
Hugin推理算法的主要步骤如下:
(1) 端正化。将贝叶斯网络中隶属于同一子节点的父节点集连接起来,并将原有网络中的有向边换为无向边,得到Gm。
(2) 三角化。在Gm中添加最少的无向边使其能够充分三角化,任一节点Xi的所有相邻节点构成一个团Gi。
(3) 将Gt转化为联合树JT。构造直接相连的两个团进行交集,生成一个节点团,利用此节点团将这两个团联接起来,得到JT。
(4) 初始化。原网络中的CPT变为JT中的分布函数,利用式(8)对各个团节点进行初始化。
(8)
(5) 消息传递。假设S为团节点A和B的分隔节点,则A向B传递消息的过程如图6所示,可表示为
(9)
(6) 概率计算。当一个JT达到全局一致,即对于任意给定的分割节点Sa、Sb,有φA=φB时,便可找到所求变量V所在的节点团,可用式(10)获得V的概率分布。
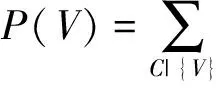
(10)
(7) 加入证据。每当获得新的证据时,使得JT处于非全局一致,计算:
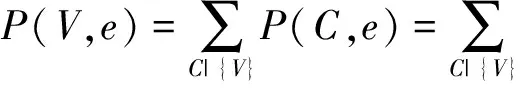
(11)
根据条件概率公式,则有
(12)
综上,即可得到新证据条件下V的概率分布。
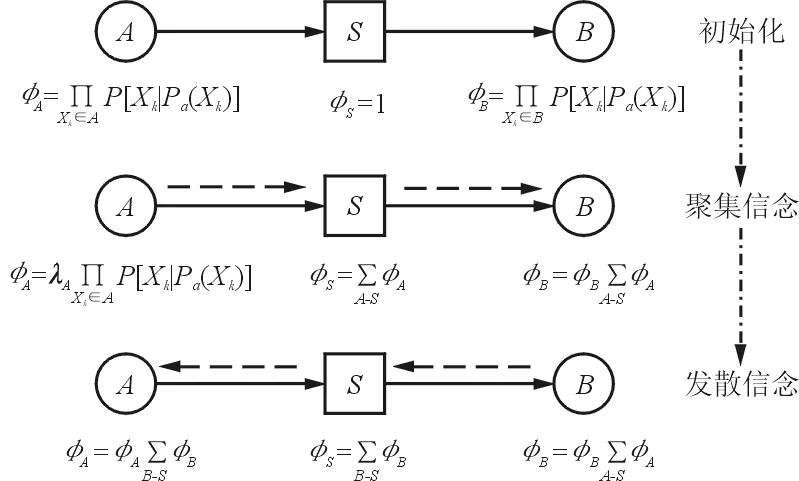
图6 Hugin的推理过程Fig.6 Reasoning process of Hugin
3.1 作战效能推理
作战效能推理是通过确定作战想定节点的取值,来获取最终评估目标节点的取值,并依此计算方案的作战效能,对方案决策等具有一定的指导作用。
由贝叶斯评估模型加入证据进行作战效能推理。假设节点HP取2(表示命中概率高),TD取2,TMK取2,进行推理,推理结果如图7所示,可以看出:在输入节点证据之后,导弹性能、杀伤能力、毁伤能力均有较好优势,但是由于敌方导弹攻击能力较强,致使我方的生存能力不高,导致结果战斗效能不高。
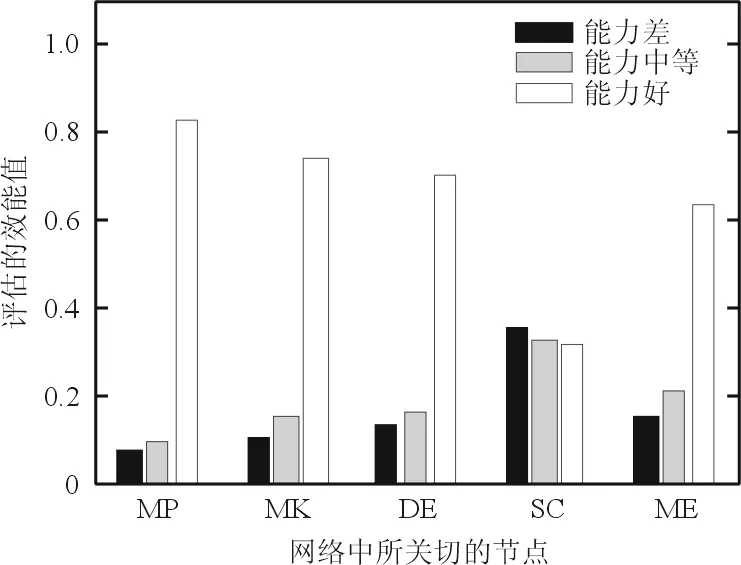
图7 加入证据后的部队效能Fig.7 Combat effectiveness with evidence
3.2 影响因素推理
影响因素推理是在假设各影响因素已知的前提下,通过贝叶斯网络效能评估模型对作战方案进行分析,从而为作战想定的改进和优化提供依据。
加入证据进行影响因素推理。假设导弹性能与敌方导弹攻击能力均一定(MP与TMK均取2),则在不同部队效能结果下,各节点的效能值变化如图8所示。
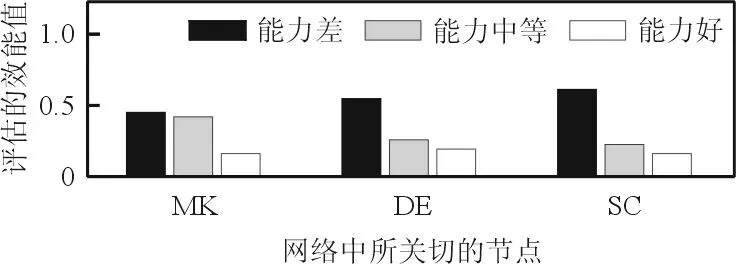
(a) 当ME取1时
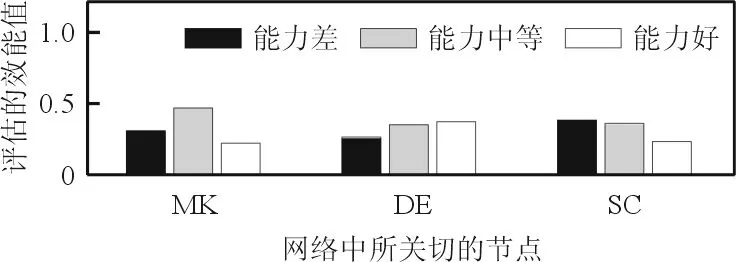
(b) 当ME取2时
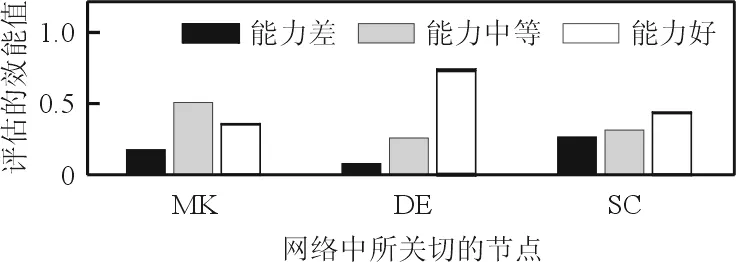
(c) 当ME取3时图8 不同部队效能值时的各节点的变化Fig.8 Nodes value with different combat effectiveness
从图8可以看出:当部队效能发生变化时,毁伤能力的变化最为剧烈,即毁伤能力的提升可极大地提升部队的整体效能。同时,提高生存能力也是提高部队效能的一种途径,但就影响大小来说,毁伤能力对部队效能的改变更大。
为了验证网络的推理能力,改变网络的证据节点,节点HP、TD取值不变2,TMK取3(敌方导弹杀伤能力强),结果如图9所示。
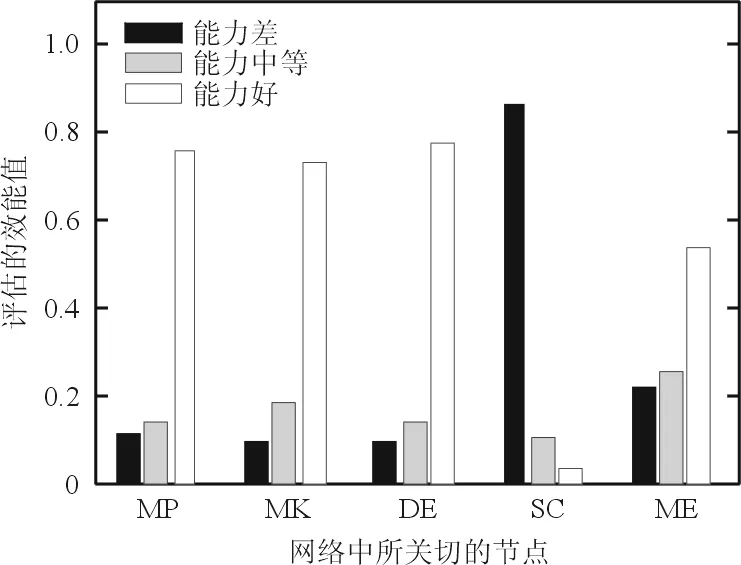
图9 加入新证据后的部队效能Fig.9 Combat effectiveness with new evidence
从图9可以看出:在新的证据条件下,当TMK为“强”时,我方飞机的生存能力明显降低,且部队效能下降,符合实际情况。
为了验证该方法的有效性,采用层次分析法做对比试验。根据专家打分法确立各个节点的权重[εMPεMKεDEεSC]=[0.15 0.22 0.35 0.28]。
对于2.1中第一种情况,得出ME=0.625 7;第二种证据下的结果为0.538 9。在从因到果的推理中,层次分析法同样可以完成评估任务,但却无法做出推理判断,无法反映下层对上层的反馈作用或者层次间各要素的相互影响。
4 结 论
本文针对战场不确定性因素多的问题,建立了协同作战效能评估的模块化贝叶斯网络模型,给出了基于贝叶斯网络的空战效能评估方法。该方法解决了现有评估方法中无法恰当反映评估要素之间复杂关联关系及作战关系中的不确定性问题,且能够向决策者提供清晰的评估过程,具有可追溯性,便于使用者根据评估结果对作战方案和作战样式进行改进和优化,具有一定的理论及实践意义。
[1] 罗继勋. 航空武器系统装备作战效能评估与系统优化[M]. 北京: 兵器工业出版社, 2004.
Luo Jixun. Operation effectiveness evaluation and system optimization of aviation weapon system equipment[M]. Beijing: Weaponry Industry Press, 2004.(in Chinese)
[2] 刘明辉. 贝叶斯网络驱动的效能仿真与评估模型建构方法研究[D]. 长沙: 国防科技大学, 2008.
Liu Minghui. Research on construction method of Bayesian network driver’s performance simulation and evaluation model[D]. Changsha: National University of Defense Technology, 2008.(in Chinese)
[3] Barry P S, Zhang Jianping, McDonald M. Architecting a knowledge discovery engine for military commanders utilizing massive runs of simulations[C]. Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 2003.
[4] Andrew Gelman, John B Carlin. Bayesian data analysis[M]. 3rd ed. CRC Press, 2014.
[5] Poropudas J, Virtanen K. Analyzing air combat simulation results with dynamic bayesian networks[C]. Proceedings of the 2007 Winter Simulation Conference, 2007: 1370-1377.
[6] 陈健, 李忠民, 王永明, 等. 基于贝叶斯网络的装备部件战斗损伤评估模型[J]. 系统工程与电子技术, 2007, 29(2): 330-332.
Chen Jian, Li Zhongmin, Wang Yongming, et al. Component battle damage assessment model based on Bayesian network[J]. Systems Engineering and Electronics, 2007, 29(2): 330-332.(in Chinese)
[7] 史志富, 张安, 刘海燕, 等. 基于贝叶斯网络的编队对地攻击损伤评估研究[J]. 系统工程与电子技术, 2007, 29(7): 1113-1116.
Shi Zhifu, Zhang An, Liu Haiyan, et al. Damage assessment of formation air-to-ground attack based on Bayesian networks[J]. Systems Engineering and Electronics, 2007, 29(7): 1113-1116.(in Chinese)
[8] 苏畅, 张恒喜. 飞机作战效能评估中人的可靠性的引入方法[J]. 航空学报, 2006, 27(2): 262-266.
Su Chang, Zhang Hengxi. Method of considering human reliability in combat effectiveness evaluation of aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2006, 27(2): 262-266.(in Chinese)
[9] 董彦非, 王礼沅, 张恒喜. 战斗机空战效能评估的综合指数模型[J]. 航空学报, 2006, 27(6): 1084-1087.
Dong Yanfei, Wang Liruan, Zhang Hengxi. Synthesized index model for fighter plane air combat effectiveness assessment[J]. Acta Aeronautica et Astronautica Sinica, 2006, 27(6): 1084-1087.(in Chinese)
[10] 周兴旺, 从福仲. 基于BP神经化贝叶斯网络的空袭目标毁伤效果[J]. 火力指挥与控制, 2016, 41(4): 20-24.
Zhou Xingwang, Cong Fuzhong. Battle eamage assessment of air-raid based on BP neuralization Bayesian network[J]. Fire Control & Command Control, 2016, 41(4): 20-24.(in Chinese)
[11] 王巍. 基于云参数贝叶斯网络的威胁评估方法[J]. 计算机技术与发展, 2016, 26(6): 106-110.
Wang Wei. An threat assessment method based on cloud parameters Bayesian network[J]. Computer Technology and Development, 2016, 26(6): 106-110.(in Chinese)
[12] David Barber. Bayesian reasoning and machine learning[M]. England: Cambridge University Press, 2016.
[13] 张连文, 郭海鹏. 贝叶斯网络引论[M]. 北京: 科学出版社, 2006.
Zhang Lianwen, Guo Haipeng. Introduction of Bayesian network[M]. Beijing: Science Press, 2006.(in Chinese)
[14] 焦松. 武器装备效能仿真评估关键问题研究[D]. 哈尔滨: 哈尔滨工业大学, 2014.
Jiao Song. Research on key problems of simulation evaluation of weapon system effectiveness[D]. Harbin: Harbin Institute of Technology, 2014.(in Chinese)
[15] 金镭, 张曙光, 孙金标. 基于仿真的空战效能评估分析研究[J]. 飞行力学, 2012, 30(1): 87-91.
Jin lei, Zhang Shuguang, Sun Jinbiao. Analysis and evaluation of air-combat effectiveness based on simulation[J]. Flight Dynamics, 2012, 30(1): 87-91.(in Chinese)
[16] 徐荣红, 孙金标, 刘峰, 等. 信息化条件下空战综合能力指标[J]. 火力与指挥控制, 2008, 33(1): 141-144.
Xu Ronghong, Sun Jinbiao, Liu Feng, et al. Research on the synthetic combat capability index of the air combat in information condition[J]. Fire Control & Command Control, 2008, 33(1): 141-144.(in Chinese)
[17] 黄解军, 万幼川, 潘和平, 等. 贝叶斯网络结构学习及其应用研究[J]. 武汉大学学报, 2004, 29(4): 315-318.
Huang Xiejun, Wan Youchuan, Pan Heping, et al. Bayesian network structure learning and its applications[J]. Geomatics and Information Science of Wuhan University.(in Chinese)
[18] 吴红, 王维平, 杨峰. 融合先验信息的贝叶斯网络结构学习方法[J]. 系统工程与电子技术, 2012, 34(12): 2585-2591.
Wu Hong, Wang Weiping, Yang Feng. Structure learning method of Bayesian network with prior information[J]. Systems Engineering and Electronics, 2012, 34(12): 2585-2591.(in Chinese)