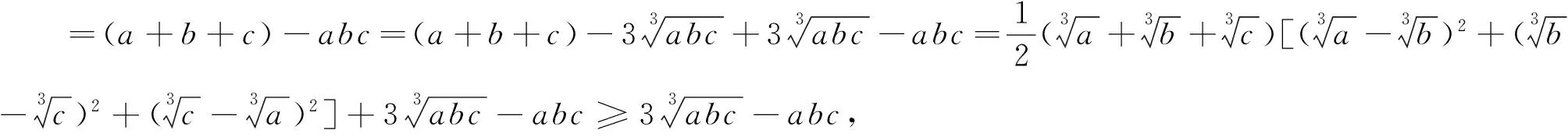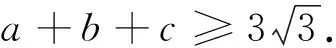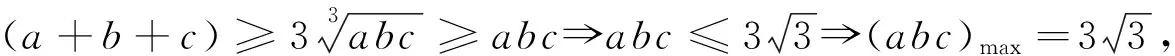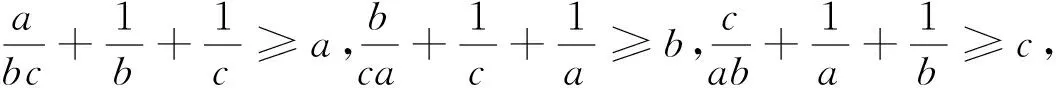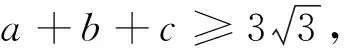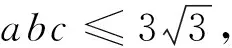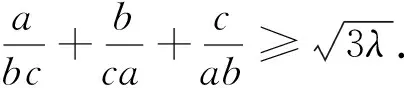一道2017年塞浦路斯数学奥林匹克试题别证

江苏省泰州市姜堰区实验初中 (225500) 沈 兵江苏省姜堰中等专业学校 (225500) 陈 宇

2017年塞浦路斯数学奥林匹克试题[1]

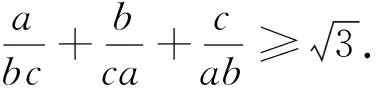
在与函数有关的问题中，我们经常会用到这样的结论[2]：若存在x1∈(a,b),x2∈(c,d)，使得f(x1)>g(x2)或f(x1)g(x2)max或f(x1)max

若x∈(a,b)，不等式k≤f(x)或k≥f(x)恒成立，求实数k的范围⟹k≤f(x)min或k≥f(x)max.

笔者在此主要依据上述结论，给出这道试题的几个别证.

证明：由题设正数a+b+c≥abc,得(a+b+c)-abc≥0.

也可由题设a+b+c≥abc得

评注:法一较之法二，法三的思路及过程明显较烦.但作为一种方法，不无可取之处.它的每一步过程几乎都是以上述所引函数结论为依据.这对培养严密的数理逻辑，灵活运用方法和知识，拓宽解题思路不无益处.

[1]吴倩倩.用基本不等式巧证2017数学奥林匹克试题[J].中学数学研究(江西师大),2017,6：47.

[2]洪建松,虞关寿.“似是而非”的几个不等式模型[J].中学数学研究(江西师大),2016,12：38.

中学数学研究ZZHHOONNGGXXUUEE SSHHUUXXUUEE YYAANNJJIIUU2018年第1期 (月刊)总第380期 2018年1月15日出版