向量数量积范围问题的解法举要

江苏省海门中学 (226100) 樊陈卫

向量数量积是向量的一种重要运算，包括高考在内的各类考试中求向量数量积的值或范围问题屡见不鲜.学生面对此类问题，如果思维单一，往往陷入束手无策的境地.本文通过不同的例子，试图揭示求向量数量积范围问题的解题策略.

一、用定义

求向量的数量积，那么什么是向量的数量积，回到向量数量积的定义中去，往往是学生首先想到思路.

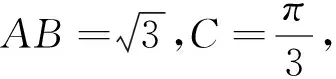
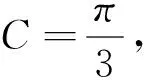
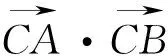
点评:向量数量积的定义，换一个视角，可理解为其中一个向量的模与另一向量在该向量上的投影之积，用投影的思路在解决已知其中一个向量模的数量积问题中可以优先考虑.

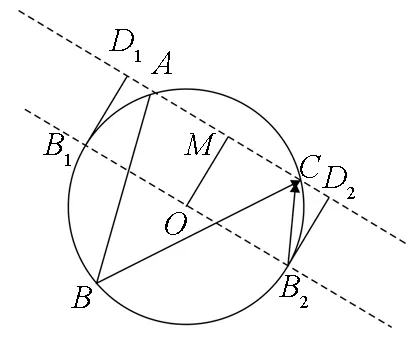
图1

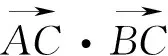
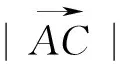
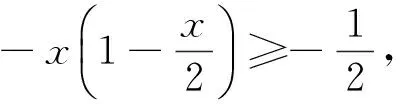
点评:从以上例题可以看出，当问题涉及向量较少，两个所乘向量的夹角，或者向量模等相关数据已知，直接用定义可以达到立竿见影之效，当然也可以引进向量模或夹角等相关变量，再应用向量数量积的定义来解决问题.

二、转基底

若问题涉及较多的向量，且所求向量的夹角或向量模不易求出，直接用向量的定义可能会碰壁，这时应及时调整思路，选择合适的两个向量作为基底，其余向量用基底向量表示，往往也是解决向量数量积问题的突破口.

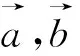
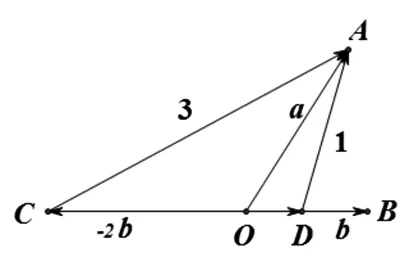
图2

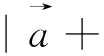
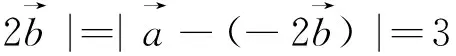
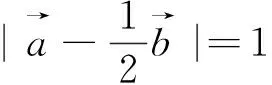
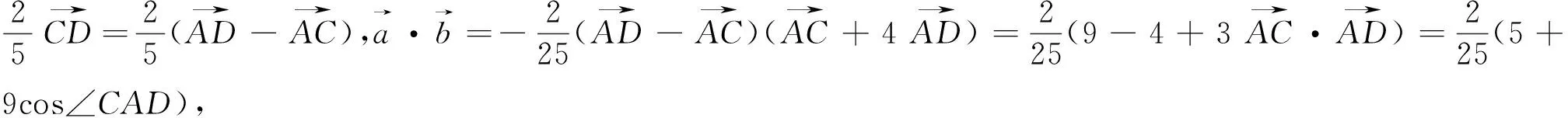
点评:从例3可以看出，用基底法的关键是基底向量怎么定.一般而言，已知向量模、夹角等相关信息较多，和其余向量联系也比较紧密的向量往往是基底向量的首选.

三、建坐标

如果不能确定哪一对向量作为基底，不妨建立平面直角坐标系，将相关向量坐标表示出来，将问题转化为数的运算解决问题.

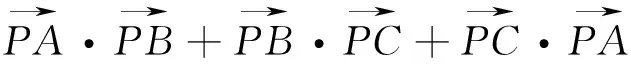
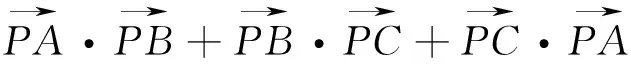
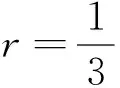
点评:本题条件中关键两个动点确定了目标式的取值，两个动点，一点在圆上，一点在圆内，如何引进变量来表示这两个活动范围不同的点，是本题能顺利解决的关键.

四、用结论

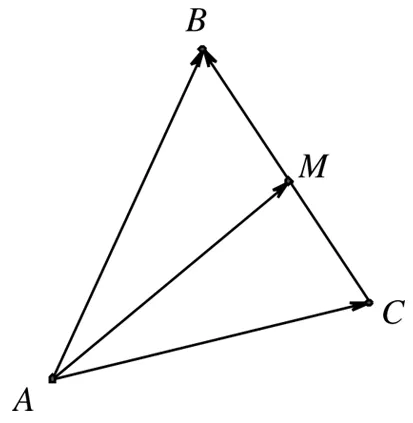
图3

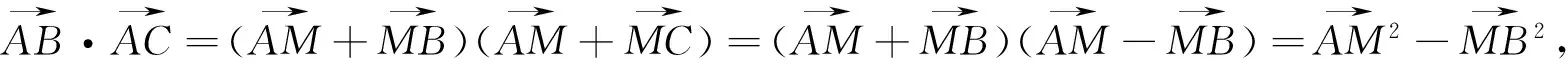
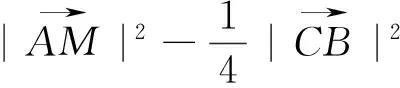
例5 如图4，在正方形ABCD中，AB=2，M,N

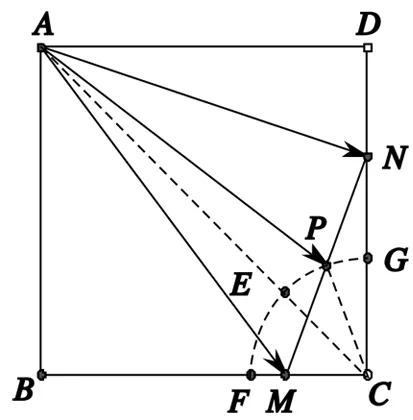
图4

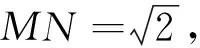
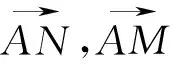
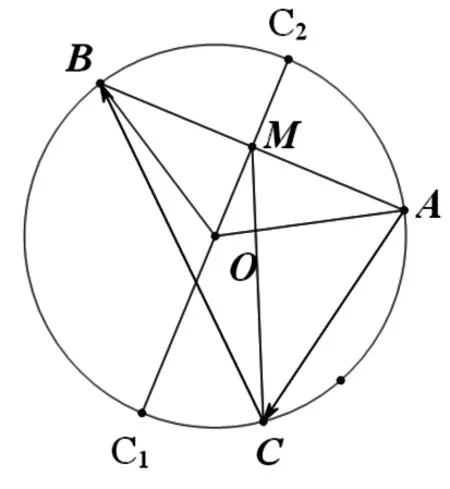
图5

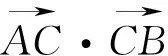
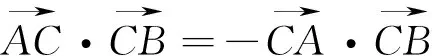
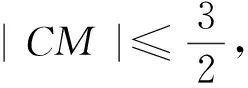
向量数量积的范围问题归根结底还是变量的范围问题，数量积的值一般由一个或多个动点的位置确定.针对题目所给的条件，引入恰当的变量，可能是点的坐标、某条线段的长度、某个角度，针对题目所给条件的特征，选择恰当的方法，往往能顺利解决问题.