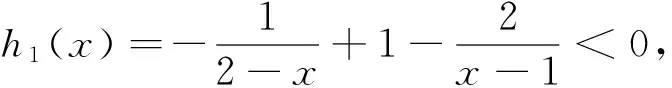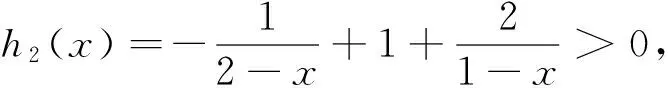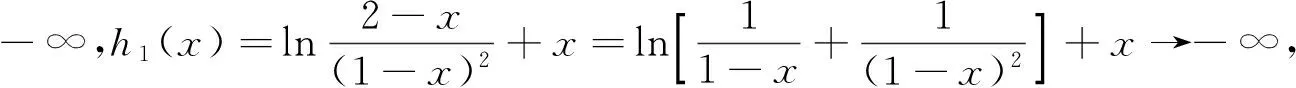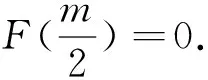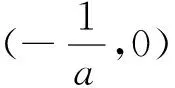规范灵活的思维是解决压轴题的关键——以展示两道函数与导数压轴题解题历程为例

山东省宁阳第一中学 (271400) 陈博文

函数与导数作为高中数学的核心内容之一，在高考命题中一直作为压轴题出现.它能充分体现考生的思维品质和精神品质，是同学们在考试中都想摘得的一颗明珠.但同学们普遍反映,在此类题型的解题过程中经常步履艰难，不知从何下手，以至于最后对其产生了畏惧之心.

其实，函数与导数题型的难度，在于它的逻辑思维战线长，中间一波三折，又可穿插考查分类讨论、数形结合等多种数学思维.在解题过程中，考生冗长的思维易出现混乱，便会出现说理不清甚至不能继续答题的情况.因此，把自己的解题思维变得规范、灵活、有条理、简洁，是十分必要的.

1.注重积累，夯实基础，养成规范的数学思维

规范的思维，首先在于如何去分析问题，解决问题，并快速地从知识储备中提取所用知识.常见题型的各种问题，每一步的操作步骤,甚至具体到在哪一点上自己易出错，都应熟记于心.基础扎实，不仅是指知识上的准确，更在于运用的熟练，即能形成一套规范的解题程序.而这种规范思维的养成，需要平时多整理、多思考、多练习.

在学习的过程中，思考很关键.解题程序牢记于心，依赖于对每一个步骤的理解.比起只刷题不思考，先思考、再利用刷题检验自己的思考成果更为高效，也更易使人养成规范的思维.下面，我用两个题目来阐述规范的数学思维的重要性.

题目1 (2017年山东卷理20)已知函数f(x)=x2+2cosx，g(x)=ex(cosx-sinx+2x-2),其中e=2.71828…是自然对数的底数.

(Ⅰ)求曲线y=f(x)在(π,f(π))处的切线方程;

(Ⅱ)令h(x)=g(x)-af(x)(a∈R)，讨论h(x)的单调性并判断有无极值，有极值时求出极值.

分析：(Ⅰ)明显是切线问题.对于这一类问题，我们的基本思维为抓住切点建方程，列出点斜式便可较快地得出答案.

(Ⅱ)是探究函数的单调性和极值.其基本步骤为：求出h′(x)，并探究它与零的关系.通过对参数讨论的手法来描绘出函数图像的特点.

解题历程：(Ⅰ)由题意可得f(π)=π2-2，故切点坐标为(π,π2-2)；又f′(x)=2x-2sinx，故f′(π)=2π，因此，切线方程l:y-f(π)=f′(π)(x-π)，整理得l:2πx-y-π2-2=0.

(Ⅱ)由题意，h′(x)=ex(cosx-sinx+2x-2)+ex(-sinx-cosx+2)-a(2x-2sinx).

自问1：h′(x)的表达式过于冗长，应该如何处理呢？

自答1：由于h′(x)的表达式过于冗长，(Ⅱ)问大部分同学因此折戟沉沙.做到这里，我们在考场上应想：我们是如何通过导数来研究图像的？我们通过讨论导数与零的关系来画出草图研究极值，但对于现在的h′(x)，我们仿佛很难讨论它与零的关系.此时，规范的程序性思维便派上了用场，对这种和差形式的导数，最通常的办法是通过因式分解求出变号零点，再进行讨论.

于是可得h′(x)=2ex(x-sinx)-2a(x-sinx)=2(ex-a)(x-sinx).

自问2：因式ex-a与零的关系需要进行分类讨论，因式x-sinx不含有任何参数，那么x-sinx与零的关系如何？

自答2：既然因式x-sinx不含有任何参数，那么x-sinx与零的关系只与变量x有关，可以新设函数，进行研究；对于因式ex-a，可令ex-a=0,即ex=a,若使得该方程有解，只需要讨论参数a与0的关系，当a≤0时，显然ex-a>0,当a>0时，方程ex=a的解为x=lna,此时需要综合x-sinx的零点进行分类讨论.

设m(x)=x-sinx,由于m′(x)=1-cosx≥0,则m(x)在R上单调递增，又因为m(0)=0，所以当x<0时，m(x)0时，m(x)>m(0)，即x-sinx>0.

设n(x)=ex-a，h′(x)=m(x)·n(x).

(1)当a≤0时，ex-a>0恒成立;则当x<0时，h′(x)<0,h(x)单调递减；当x>0时，h′(x)>0，h(x)单调递增；当x=0时有最小值h(0)=-2a-1，无极大值.

(2)当a>0时，令ex-a=0得x=lna.

①若lna<0,即00，因此h(x)在(-∞,lna)上单调递增；无极值；

②若lna=0，即a=1，当x<0时，m(x)<0,n(x)<0,故h′(x)>0，因此h(x)在(-∞,lna)上单调递增；无极值；

③若lna>0，即a>1，当x<0时，m(x)<0,n(x)<0,故h′(x)>0；当0lna时，h′(x)>0，h(x)在(lna,+∞)上单调递增；因此x=0时，h(x)取到极大值，h(0)=-2a-1，x=lna时，h(x)取得极小值为h(lna).

综上(1)、(2)分类，便可得最终答案.

评注：细思本题，仍然考查处理函数与导数问题的通性通法，本题能作为压轴题，重点在于考查数学的基本功，如因式分解、分类讨论等，只不过对这些通性通法的考查，换了复杂的函数背景，为了克服这种背景陌生，由于思维过程冗长带来的解题失分，我们在日常的复习过程中，应该注入研究性思维，将理论知识转化为我们切实可行的解题程序，寻找万变不离其宗之“宗”，揭示问题的本质.例如本题涉及到的切线问题，核心在于抓住切点建方程，那么由切点引发的结论是什么？切点可得切线斜率、切点在切线上、切点在曲线上，利用关于切点的这三条，关于切线甚至于较难的问题我们也会迎刃而解；对于(Ⅱ)问，我们要始终确信，在我们应该掌握的知识范畴内，只要研究导数，就一定是研究导数与0的关系，知道了导数与0的关系，我们也就清楚了单调性、极值点的问题了，对于分类讨论，是因需要才讨论，不是去欣赏怎样讨论对不对的问题，而是解决为什么要讨论的问题，很明显，弄清楚了两个因式m(x),n(x)与零的关系，我们得到了关于参数a的一级讨论点“0”，但又无法区分两因式与0的关系，需要比较lna与0的大小，从而得到了关于参数a二级讨论点“1”，综合起来，即对a的讨论分为a≤0,01.这就是规范的思维总结.

2.善于观察，寻找联系，注重灵活的解题思维

对于函数与导数部分出现的新情景、新问题，要善于观察问题结构，寻找函数问题的内在联系，可使用分析法、综合法等方式与已知建立联系，从而找到解题的突破口.

题目2 (2016年全国新课标卷Ⅰ理21)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点.

(Ⅰ)求a的取值范围;

(Ⅱ)设x1,x2是f(x)的两个零点，证明x1+x2<2.

分析：(Ⅰ)对于零点的问题，我们常用的方法是含参讨论函数形态，或者采用分离参数的方法化为常数函数与其它函数交点个数来解.

(Ⅱ)观察求证x1+x2<2，问法新颖，如何将此问转化为函数破解是解决本题的关键，不妨结合第一问采用分析法解之.

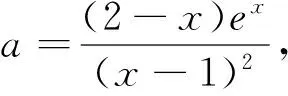
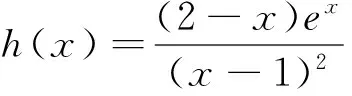
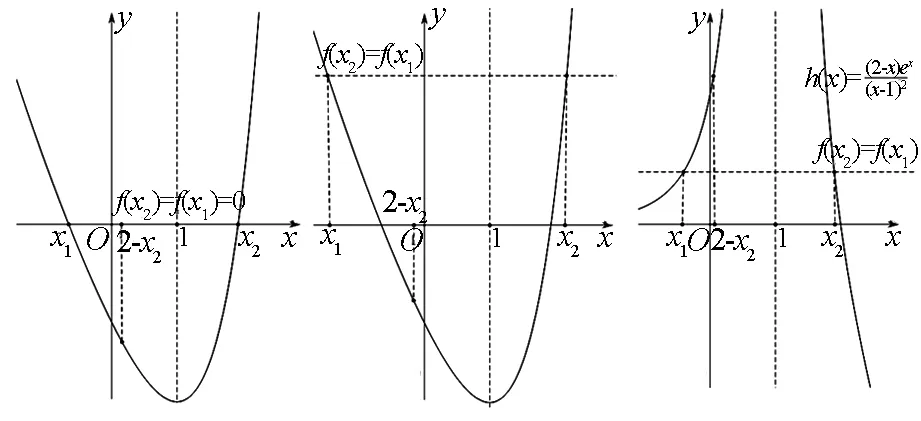
令f(x)=0,即得(x-2)ex=-a(x-1)2，显然a=0不满足两个零点的条件，从而x=2,x=1也不是函数f(x)的零点.

(1)若a<0，则x>2,从而(x-2)ex>0,

-a(x-1)2>0，两边取以“e”为底的对数，可得ln(x-2)+x=ln(-a)+2ln(x-1),即ln(x-2)+x-2ln(x-1)=ln(-a).

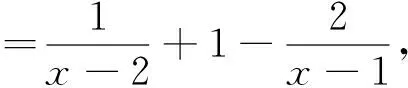
(2)若a>0，则x<2，(x-2)ex=-a(x-1)2可化为(2-x)ex=a(x-1)2，当1

(1,2)上单调递减，又x→1,h1(x)→+∞,x→2,h1(x)→-∞，函数y=lna与函数h1(x)在(1,2)上仅有一个交点；当x<1,则函数(x-2)ex=-a(x-1)2可化为ln(2-x)+x=lna+2ln(1-x),即

ln(2-x)+x-2ln(1-x)=lna.

(-∞,1)上单调递增，又x→1,h2(x)→+∞,x→

(Ⅱ)自问2：由(Ⅰ)可知，若x1,x2是f(x)的两个零点，则a>0，若设x1

自答2：若证x1+x2<2成立，只需证明x1<2-x2，而2-x2<1，那么x1,2-x2均在“1”的左侧.那么如果知道函数f(x)在(-∞,1)上的单调递减，则只需证明f(x2)=f(x1)>f(2-x2).

解题历程：易得f′(x)=(x-1)ex+2a(x-1)=(x-1)(ex+2a).

在(Ⅰ)已得到a∈(0,+∞)，明显 因式ex+2a>0在R上恒成立.所以，x∈(-∞,1)，f′(x)<0,x∈(1,+∞)，f′(x)>0.f(x)在(-∞,1)上单调递减，在(1,+∞)单调递増.要证x1+x2<2，只要证x1<2-x2.不妨设x1f(2-x2),即f(x2)-f(2-x2)>0.

设F(x)=f(x)-f(2-x)=(x-2)ex+xe2-x(x>1)，则F′(x)=(x-1)(ex-e2-x),因为x>1，F′(x)>0在x∈(1,+∞)上恒成立，即F(x)在(1,+∞)上单调递增，故F(x)>F(1)=0.

因x2>1,则F(x2)=f(x2)-f(2-x2)=f(x1)-f(2-x2)>0,即f(x1)>f(2-x2)，命题得证.

评注：解完后回思，本题总体的难度就体现在解题方法的选择和对问题的处理技巧上.而找出一个即快又准的办法，是解决这类创新型题目的关键.对于(Ⅰ)问，虽然考察的是常见的零点个数问题，但就其运用先讨论等式两侧正负，再等式两边同取对数的手法，还是对逻辑思维能力的一个较大考验.这就要求我们在平常的学习中多探究，多总结.如：在什么时候我们采取“取对数”的手法能大大降低试题难度呢？通过对本题的剖析，我们可发现：取对数的作用就是将因式拆分.对于等号两边同为乘积式的等式，我们取对数便可将乘积拆分.但我们应注意，只有在参数单独自为因式(不与自变量同因式)时，我们的分离才是有效的.如将题(Ⅰ)中的等式改为(x-2)ex=-(a-x)(x-1)2，再通过取对数的手法进行处理，得到的仍是含参问题，这样的套用无异于南辕北辙.因此要明确，我们取对数的目的是将参数分离出来，以免去之后的含参讨论函数形态.而对于(Ⅱ)问，考察的本质仍是函数问题，但具体考察意向并不像上问一样直白.这要求我们突破常规问题的思维禁锢，抽丝剥茧，抓住问题的本质.该问实际上是在让我们描述函数图像的细节：函数f(x)在x=1左侧的图像的斜率绝对值始终小于右侧图像的绝对值.题目正是通过一个关于零点的不等式刻画了函数图像“偏对称”这一特点，而我们要做的只是将函数图像的这一特点用代数表达、证明.如果我们认识到了这一点，想到运用对称设法，构建新的函数也就变得自然而然了.因此，想要解决这类新颖的题目，真正理解手法的原理，剖析问题的本质才是治本之策，这也是训练灵活的解题思维所必须的.

图1 图2 图3

题目2变式已知函数f(x)=ln(ax+1)-ax-lna.

(Ⅰ)讨论f(x)的单调性;

因此，对于我们已经解过的题型，要具体问题具体分析，找到问题异同点，灵活运用，趋利避害，才能在考场上精准解答.

规范、灵活的数学思维的养成，对导数与函数大题的解决起到了至关重要的作用，是解题思路条理清晰的前提.为提高我们的逻辑思维能力，在考试中突破分数瓶颈，我认为在平常学习中应做到以下二点：一是数学思维的养成，需要做到“整理、思考、练习”，步步为营.平时多问自己几个为什么，加强对解题步骤中细节的揣摩，将其思想融到心中，才能在旧题型上做到既快又准，在新题型上有所突破.二是数学学习是一个循序渐进的过程.对函数与导数的理解也是如此，问题的深入也是思维的升华，不断地自问自答同样也是循序渐进学习的过程，我们平时多独立思考，总结并积累自己的解题模式并加以必要的练习，才能在考场上游刃有余.

如果说数学考试是一场思维的博弈，那函数与导数便是其最精彩的部分.希望同学们能静下心来，去感悟数学思维的魅力，在对数学的探究中找到自己的乐趣！