图解法在解决平面向量一类问题中的应用

安徽省阜阳市第三中学 (236000) 凡胜富安徽省阜阳市颍泉小学 (236000) 蒋 娟

向量是几何与代数交汇的数学知识，融“数”“形”于一体.为此，在解决平面向量的某些问题时，如果能抓住向量既具有数又具有形的特征，运用数形结合的思想，根据题目中的已知条件，恰当地构造出符合题意的图形，利用图解法去分析或发现其中隐藏的几何性质，往往能达到事半功倍的效果.下面举例说明之，供读者参考.

1.利用几何意义构造图形来处理

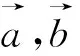
A.30°B.60°C.120°D.150°

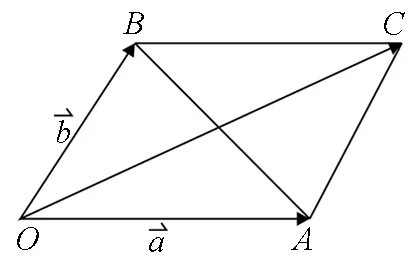
图1

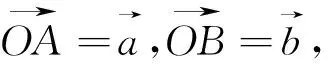
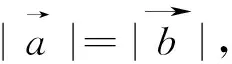
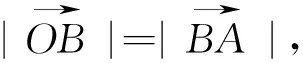
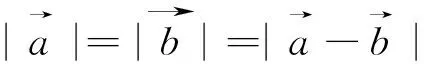
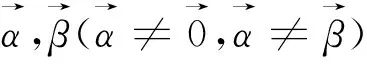
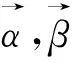
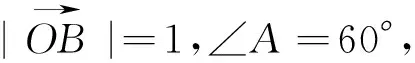
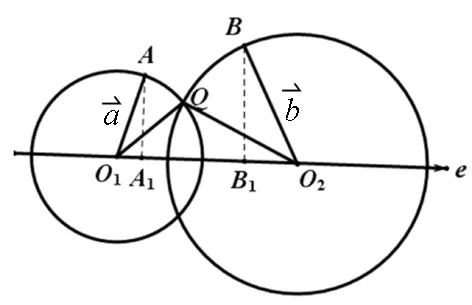
图3

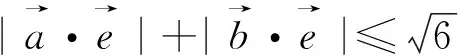
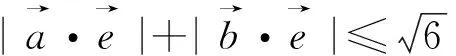
2.定向量与动向量考虑用投影处理

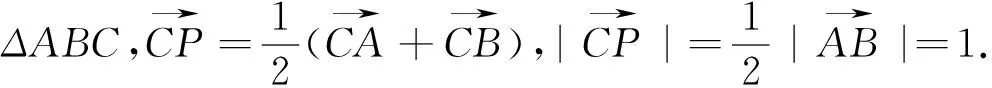
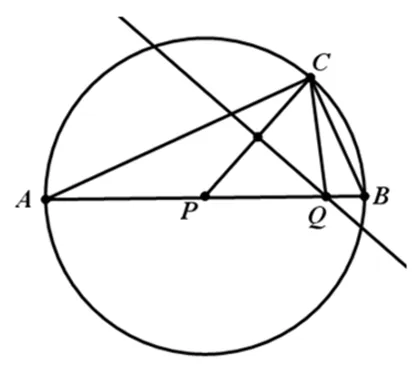
图4

解：根据已知条件，CP为ΔABC的边AB上的中线，且其长度为AB的一半，因此ΔABC为直角三角形，且C为直角.如图4.

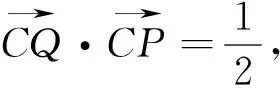
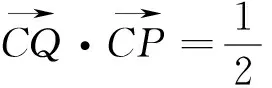
3.两动向量考虑用极化恒等式处理

图5

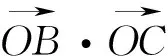
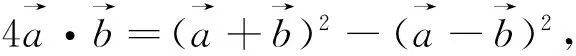
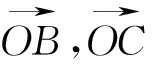
链接高考

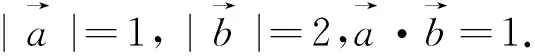
3、(2016江苏卷﹒理13)如图6，在ΔABC中，D

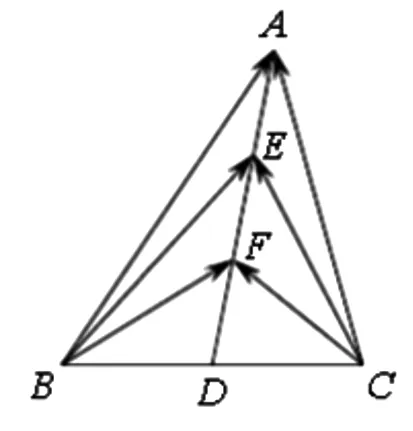
图6

高中阶段的平面向量运算都具有明显的几何意义，充分抓住平面向量的几何特征，从“形”这一角度打开思维入口，继而将向量问题转化为平面几何问题借助数形结合处理，该做法是向量试题中较为常见且隐蔽性又较强的一种处理策略，它对学生综合分析、运用知识的能力提出了一定的要求，要求学生具有较好的数学素养，同时也更好地提高了学生分析问题、解决问题的能力．

[1]刘胜林.向量试题中的几种求解视角[J].数学通讯，2015(3)：3-4.