胶层对加速度计零位偏值误差的影响研究*

郭 彩，孙屹博，罗 怡，王晓东

(1.大连理工大学 辽宁省微纳米技术及系统工程重点实验室，辽宁 大连 116024；2.大连交通大学 机械工程学院，辽宁 大连 116028)

0 引 言

加速度计是一种典型的惯性器件，其性能直接决定了惯性导航系统的精度[1,2]。赵桂玲等人提出了一种基于空间笛卡尔坐标系转换的石英挠性加速度计线性标定误差建模方法[3]。聂鲁燕等人根据温度对加速度计输出特性的影响机理，给出了加速度计输出模型温度系数[4]。严斌等人设计了一种用于温漂补偿的高精度测温电路，以提高加速度计的零偏稳定性[5]。刘艳霞等人提出了一种椭球拟合法确定误差模型，实现对加速度计误差补偿[6]。张习文研究了由摆片变形引起的零偏的温度稳定性，针对摆组件的胶黏接工艺提出了改进方法[7]。Levy R等人在振动梁中间设计了扭转模式谐振器，通过实验证实了改进后的加速度计性能更好[8]。Myers D R等人利用热膨胀系数不匹配引起的热应力补偿了弹性模量的温漂系数引起的频率温漂[9]。Alaluev R V等人提出了一种加速度计比例因子的高精度补偿电路，并通过理论和实验验证了该电路的适用性[10]。

当前尚无针对胶层几何误差对加速度计零位偏值误差的影响开展研究。而在实际装配中，由于零件小，胶的黏度较大，且人工涂胶存在随机性，因此,必然产生装配误差。加之胶黏剂弹性模量小、热膨胀系数大，由胶层几何误差对加速度计零位偏值误差产生的影响不容忽视。本文针对某型号光电加速度计的胶黏剂的几何误差对加速度计的零位偏值误差的影响展开分析。

1 胶层几何误差影响理论分析

该型号加速度计中各零件之间的连接方式为胶黏接，胶黏剂采用温度为120 ℃的高温固化的方式进行固化。当加速度计从固化温度冷却至室温时，胶层几何误差必然使得加速度计内部的热应力与弹性变形存在差异，从而产生零位偏值误差。在装配过程中，人工涂胶产生的误差主要包括胶层厚度误差与接触面积误差，本文针对这两种误差对加速度计零位偏值误差的影响展开研究，分析由此产生的热应力和弹性变形，并基于图1的连接结构进行了理论推导。

图1 两零件连接简图

由于两零件相互制约，降温后，零件1受拉力，其实际变形量大于自由膨胀量，零件2受压，其实际变形量小于自由膨胀量，则零件1，2总的收缩量分别为

(1)

(2)

两零件固定在一起，其长度始终相等

(3)

两零件处于平衡状态，根据牛顿第三定律知

σ1A1=-σ2A2

(4)

由式(3)、式(4)联立解得

σ1=-kα1E1(T1-T0)

(5)

(6)

ε1l=-kα1(T1-T0)l

(7)

(8)

式中α1,α2为热膨胀系数，假设α1>α2；T1，T0分别为当前温度和初始温度；E1，E2为弹性模量；σ1,σ2为热应力；ε1，ε2为弹性应变；A1，A2为横截面积；l为两零件的有效连接长度。

可知，当零件的材料属性一定时，零件的热变形量与二者的有效连接长度l和两零件的横截面积A有关。

2 加速度计热力学模型建立

采用SolidWorks三维软件对加速度计进行建模，将已固化的胶层作为零件添加到加速度计的整体模型中，且忽略线圈等零部件，模型如图2所示。将创建的装配体导入到ABAQUS软件中，赋予相应的材料参数如表1所示。本文研究的是稳态时的零位偏值，属于稳态热力学问题，忽略了热传导过程。此外在初始时刻，将加速度计在固化温度时的状态设定为无应力状态，仿真仅考虑了加速度计由胶层固化温度降到室温时产生的零位偏值。

表1 零件材料参数

图2 加速度计挠性模块结构简图

3 胶层几何误差的有限元仿真结果与讨论

3.1 胶层厚度因素分析

加速度计中的胶层主要有4部分，从底座到三角架依次标记为胶层1,2,3,4，其分布如图3所示。

图3 胶层分布示意

本文针对4个胶层的厚度对加速度计零位偏值误差的影响展开分析。首先，将初始环境温度设为120 ℃，随后降至室温25 ℃，提取挡光板的位移，与理想涂覆状态下产生的位移作差值计算，并折算为加速度计零位偏值误差。基于以上论述，根据胶层厚度的设计尺寸为10 μm，则以理想状态胶层厚度10 μm为参照，所得零位偏值为720 μgn，加速度计的位移云图如图4所示。

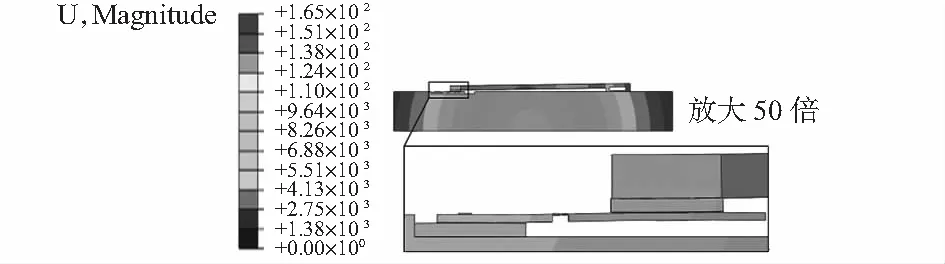
图4 加速度计位移云图

分别将各部分胶层厚度设置为6,8,10,12,14 μm，各胶层不同厚度引起的零位偏值误差如图5(a)所示。结果表明胶层厚度越大，加速度计的零位偏值误差越大，其中，由胶层1与胶层3引起的零位偏值误差的变化趋势一致，由胶层2与胶层4引起的零位偏值误差的变化趋势一致。这是因为胶层1与胶层3、胶层2与胶层4在加速度计中所处的位置相似，降温后，胶层向热膨胀系数大的一侧弯曲。由于零件的热膨胀系数不一致，降温后，零件之间相互制约产生剪切应力，使得零件发生翘曲变形。以胶层1为例，当零件间的有效连接长度不变时，胶层厚度越大，剪切应力越小，剪切应力分布如图5(b)所示，胶层1所在区域的翘曲变形越小，挠性梁向上翘曲越大，由此产生的零位偏值误差也越大，胶层3与胶层1类似；同理,可得胶层2,4对加速度计零位偏值误差的影响规律。根据上述结果知由胶层厚度的变化引起的加速度计零位偏值误差从大到小依次为胶层4、胶层2、胶层3与胶层1。

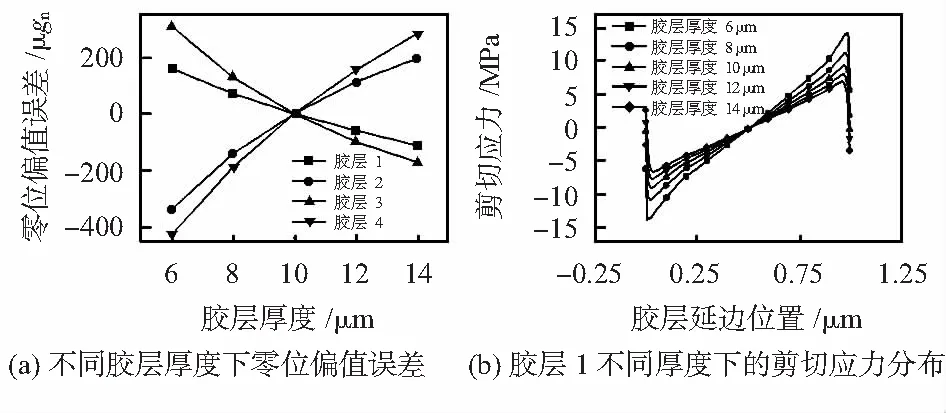
图5 不同胶层厚度产生的零位偏值误差与剪切应力分布

为了更好描述胶层厚度对加速度计零位偏值误差的影响程度，对各胶层下的零位偏值误差进行单位化处理，结果如表2所示，其中ΔL为胶层厚度变化量，|K0|为零位偏值误差的绝对值，|K0|/ΔL为单位胶层厚度引起的零位偏值误差，根据表中数据知胶层1～4引起的零位偏值误差分别为33.88,66.5,59.85,88.53 μgn/μm，胶层4对加速度计零位偏值误差的影响最大、胶层1最小。因此,在装配过程中，要想将胶层厚度误差引起的加速度计的零位偏值误差控制在50 μgn内，需将胶层厚度控制在0.5 μm内。

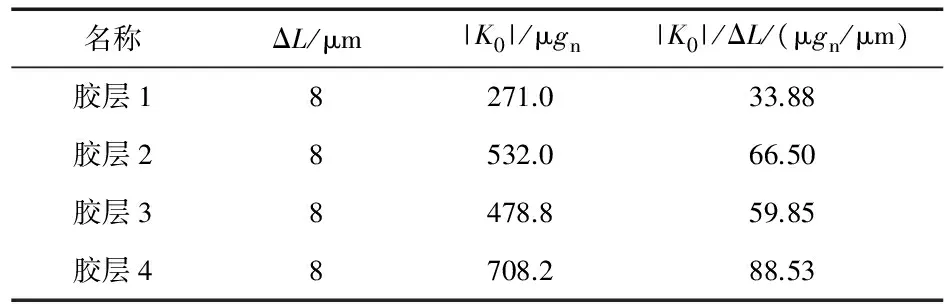
表2 胶层厚度与零位偏值误差的对应关系

3.2 胶层整体涂覆面积因素分析

在涂胶工艺中，理想状态是胶黏剂完全涂覆于零件表面，且零件边缘无溢出，但在实际装配中，由于人工涂胶存在随机性，必然产生胶黏剂不能完全覆盖零件表面的现象，本文针对该误差对加速度计零位偏值的影响展开了研究。为了便于量化分析，将胶层面积误差简化为胶层面积整体缩减，以胶层面积作为变量，研究其变化对零位偏值误差的影响。

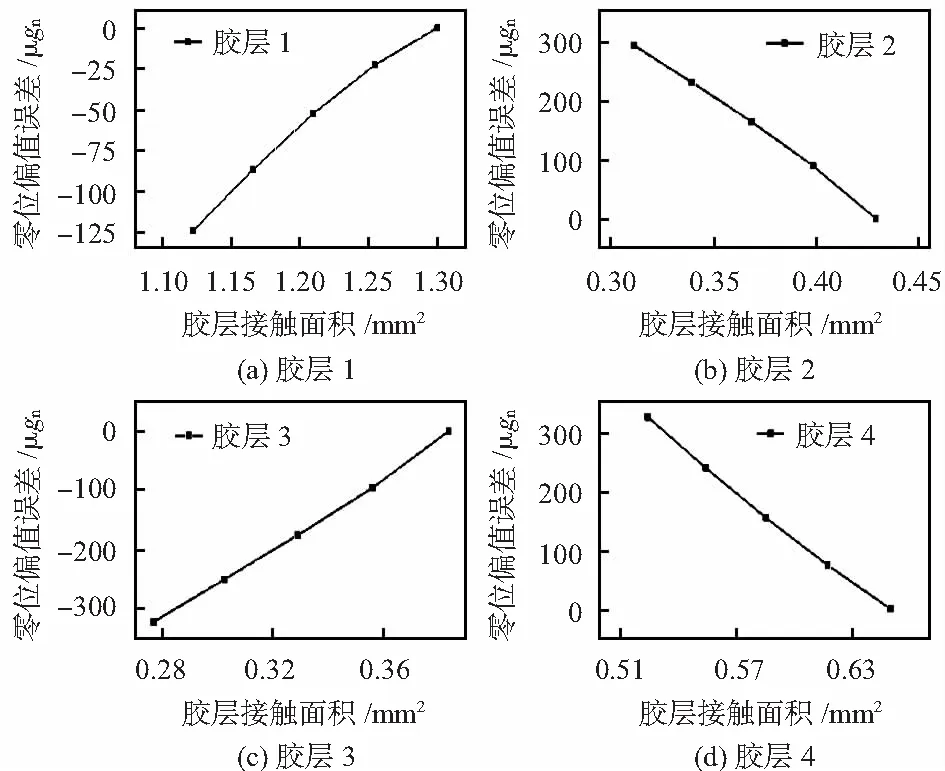
图6 胶层面积与零位偏值误差的对应关系

本文分别针对4个胶层分析了胶层面积减小对应零位偏值的变化，胶层边缘距离完整涂覆的理想位置缩进量分别设定为10,20,30 μm和40 μm，4个胶层分别缩减后胶层面积与零位偏值误差的对应关系如图6所示。根据仿真结果知由胶层1～胶层4接触面积变化引起的加速度计的零位偏值误差依次为-124.2，294.2，-322.8，326 μgn。结果表明:随着胶层1、胶层3的接触面积的减小，加速度计的零位偏值误差增大，而胶层2、胶层4与之相反。以理想状态为参考，当温度从120 ℃降到室温时，位于陶瓷两侧的胶层发生收缩变形，由于陶瓷的热膨胀系数较小，因此,收缩量也相对较小，从而产生阻碍两侧胶层变形的热应力较小，根据牛顿第三定律知，位于陶瓷两侧的胶层对其产生的作用力相互平衡。随着胶层1与陶瓷接触面积的减小，这种平衡被打破，此时胶层2对陶瓷的作用力大于胶层1的，陶瓷向上翘曲，使得两胶层对陶瓷的作用力达到新的平衡。由于加剧了陶瓷的弯曲程度，从而产生更大的零位偏值误差。

表3 胶层接触面积与零位偏值误差的对应关系

为对比分析各胶层面积减小所引起的加速度计零位偏值的变化，对各胶层下的零位偏值进行单位化处理，结果如表3所示，其中,S为理想状态时的胶层接触面积，ΔS为胶层缩减面积，|K0|为零位偏值误差的绝对值，ΔS/S为接触面积的相对变化量，|K0|/ΔS为单位面积变化量产生的零位偏值误差。根据表中数据知胶层1～胶层4引起的零位偏值误差分别为698.75，2 493.22，2 988.89 μgn/mm2与2 587.3 μgn/mm2，因此,胶层3对加速度计零位偏值误差的影响最大、胶层1的影响最小。这是因为相较于其他胶层的接触面积的相对变化量，胶层1的接触面积的相对变化量比较小，因此,由其引起的合力的变化量也较小，导致挠性梁的翘曲程度变化不大，产生的加速度计的零位偏值误差的变化也较小。因此,在装配过程中，将胶层面积误差控制在0.02 mm2内时，可将胶层面积误差引起的加速度计的零位偏值误差控制在50 μgn内。

4 结 论

本文从胶层厚度误差与涂覆面积误差2个方面展开分析,通过仿真实验得到与挠性梁和三角架接触的胶层厚度误差和接触面积误差对其零位偏值误差有较大影响，具体结论如下：

1)胶层厚度因素方面，胶层4的厚度误差对加速度计零位偏值误差影响显著，约为88.53 μgn/μm，而胶层1的厚度误差对加速度计零位偏值影响较小，约33.88 μgn/μm。因此,在装配过程中，要想将胶层厚度误差引起的加速度计的零位偏值误差控制在50 μgn内，需将胶层厚度控制在0.5 μm内。

2)胶层涂覆不足因素方面，胶层3的接触面积误差对加速度计零位偏值误差的影响最大，约2 988.89 μgn/mm2，胶层1的接触面积误差对其影响较小，约为698.75 μgn/mm2。因此,在装配过程中，将胶层面积误差控制在0.02 mm2内时，可将胶层面积误差引起的加速度计的零位偏值误差控制在50 μgn内。

[1] 于湘涛,张菁华,杜祖良.石英挠性加速度计参数长期重复性技术研究[J].导航定位与授时,2014(1):58-62.

[2] 李永光.高精度加速度计标定与补偿技术研究[D].哈尔滨：哈尔滨工业大学,2011:1-1.

[3] 赵桂玲,郭文婧,李 松.三轴一体石英挠性加速度计标定数学建模与误差分析[J].传感器与微系统,2016,35(8):15-19.

[4] 聂鲁燕,刘晓东,吴 畏,等.高精度加速度计温度特性及补偿方法[J].物探与化探,2015(S1):33-36.

[5] 严 斌,尹永刚,董景新.常温下硅微谐振加速度计零偏稳定性的提高[J].光学精密工程,2016(5):1050-1056.

[6] 刘艳霞,方建军,杨清梅.基于椭球假设的三轴加速度计误差标定与补偿[J].传感器与微系统,2014,33(6):52-54，64.

[7] 张习文.微小型加速度计的精密装配及影响性能的因素研究[D].大连：大连理工大学,2013：38-41.

[8] Levy R,Traon O L,Masson S,et al.An integrated resonator-based thermal compensation for vibrating beam accelerometers[C]∥2012 IEEE Sensors Proceedings,Taipei,Taiwan,IEEE,2012:1-5.

[9] Myers D R,Azevedo R G,Chen L,et al.Passive substrate temperature compensation of doubly anchored double-ended tuning forks[J].Journal of Micro-electro-mechanical Systems,2012,21(6):1321-1328.

[10] Alaluev R V ,Ivanov Yu V,Malyutin D M.High-precision algorithmic compensation of temperature instability of accelerometer’s scaling factor[J].Automation and Remote Control,2011,72:853-860.