敏感SVD和EEMD的故障诊断方法研究*

齐 鹏，范玉刚，冯 早

(1．昆明理工大学 信息工程与自动化学院，云南 昆明 650500；2．云南省矿物管道输送工程技术研究中心，云南 昆明 650500)

0 引 言

轴承振动信号的早期微弱故障特征易被背景噪声所掩盖，若要提取表征轴承运行状态的有效信息，需对轴承振动信号进行预处理。奇异值分解(singular value decomposition，SVD)可有效降低背景噪声对特征提取的影响[1]，但如何选择有效奇异值重构信号进而提取纯净的特征信息仍是目前的主要研究问题，赵学智教授等人提出根据奇异值曲率谱/差分谱选择有效奇异值进行信号重构[2,3]，耿宇斌等人提出对时频系数矩阵进行SVD分析时，其表征故障信息的奇异值随信噪比的减小而逐渐向后偏移[4]，此时若使用奇异值曲率谱/差分谱选择前几个奇异值重构信号，难免会导致部分噪声信息的混入，影响故障特征的有效提取。鉴于此，本文提出敏感SVD(SSVD)方法用于解决复杂工况下奇异值选择难的问题，采用敏感因子筛选反映故障特征的分量信号，并通过定位因子确定分量信号所对应的奇异值，据此重构信号，以降低噪声干扰，从而凸显反映故障信息的周期冲击成分。由于轴承振动信号具有非平稳、突变性等特点，经单一时域分析法处理，所得振动信号仍为高低频混合的多分量调幅—调频信号，因而难以准确描述轴承当前工作状态，需进行下一步处理[5]。

总体平均经验模态分解(ensemble empirical mode decomposition，EEMD)是在总结现有时频分析方法优缺点的基础上提出的一种自适应时频分析方法，该方法在抑制端点效应、模态混叠等方面都明显优于经验模态分解(empirical mode decomposition，EMD)等方法，可有效将复杂工况信号分解为由高频到低频有序分布的单分量调制信号，以凸显振动信号的局部特征[6]。

本文在研究敏感SVD降噪方法基础上，将其与EEMD时频分析方法相结合，提出了一种基于敏感SVD和EEMD的故障诊断方法,可准确定位故障特征频率，判别轴承故障类型。

1 敏感SVD降噪

1.1 基于Hankel矩阵的奇异值分解[7]

假定某机械系统的故障测试信号为X=[x1,x2,…,xn]，使用此信号构造Hankel矩阵如下

(1)

式中 1

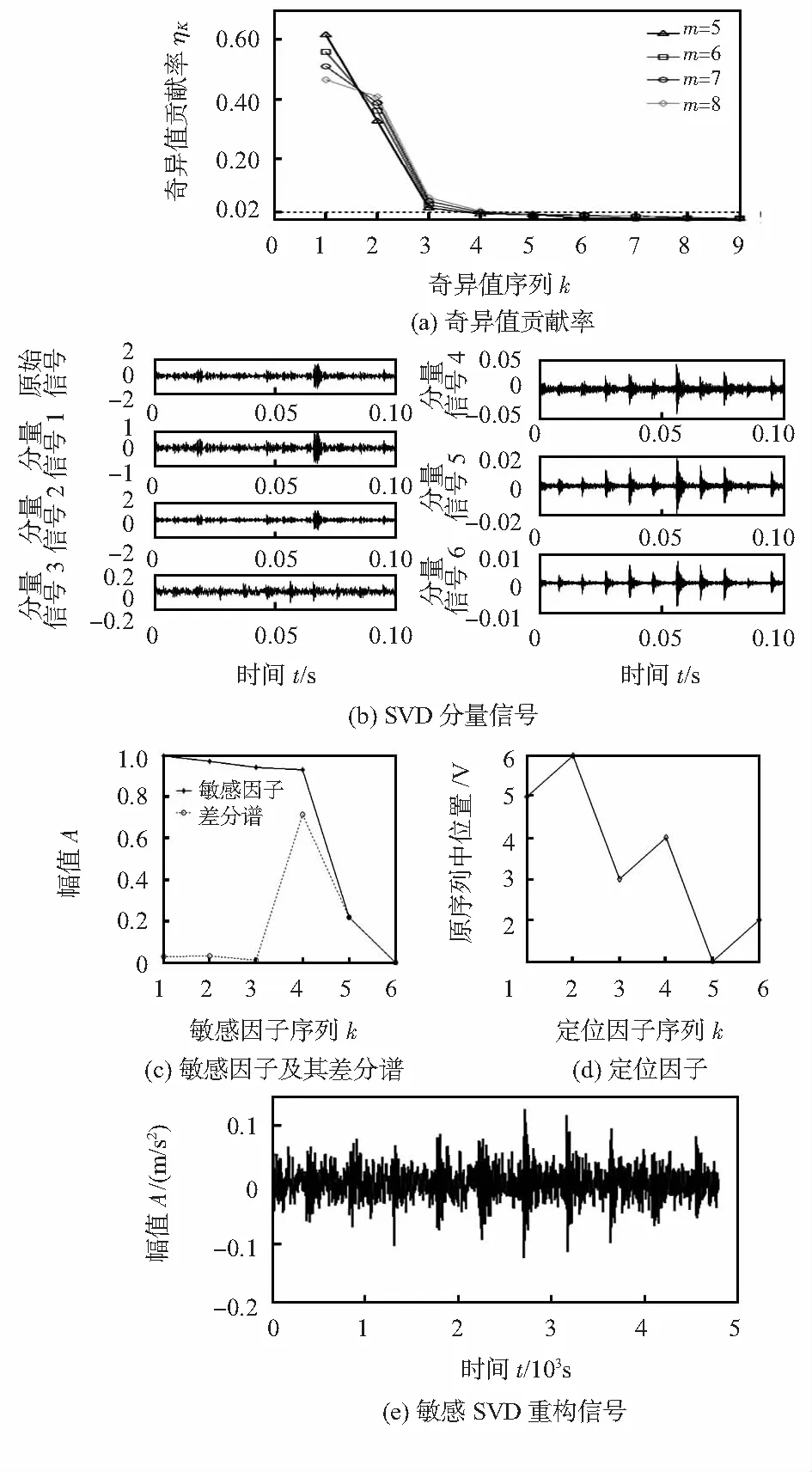
1.2 振动信号的敏感度评估与重构

本文将敏感度评估算法[9]引入SVD算法中，主要通过计算SVD分量信号与正常信号之间的相关系数及原始振动信号与其SVD分量信号的相关系数来确定敏感SVD分量，具体实现步骤如下：

1)计算待分析振动信号其SVD分量信号与正常振动信号之间的相关系数Xn，n=1,2,…,M，其中，M为分量信号的个数，下同。

2)计算待分析振动信号与其SVD分量信号之间的相关系数Yn，n=1,2,…,M。

3)根据以上两步所得相关系数Xn，Yn，求解故障相关系数Zn，公式如下

Zn=Xn-Yn,n=1,2,…,M

(2)

4)综合故障相关系数Zn，从而求得SVD分量信号的故障敏感因子Pn如下

Z={Zn} ,n=1,2,…,M

(3)

5)将所得敏感因子Pn从大到小进行有序排列，得到新的序列如下

(4)

6)根据敏感因子新序列计算相邻敏感因子之间差值，并构建敏感因子差分谱，自适应找出最大差值所对应的序列号k，则前k个SVD分量信号即为故障敏感信号。

7)由于敏感因子由大到小排列打乱了原始奇异值顺序，本文通过定位因子Qn找出前k个敏感SVD分量信号所对应的奇异值，将其进行有序排列，据此完成信号重构，以削弱噪声影响，从而凸显微弱冲击信息。

2 基于EEMD的微弱故障特征提取

由于滚动轴承故障多具有随机性、非线性等特点，其振动信号通常表现为多分量的调幅—调频信号。为了有效提取表征轴承故障的局部突变信息，需有效将多分量振动信号分解为单分量的局部特征信号。Wu Z H等人提出的EEMD信号处理方法是对EMD方法所存在缺陷的有效改进，其分解所得IMF分量信号具有一定的物理意义，可有效反映原始信号局部特征，适用于分析调幅—调频信号[10]。

2.1 振动信号的EEMD

为了有效改善EMD存在模态混叠的现象，通过在原始振动信号中多次添加频率均匀的高斯白噪声，之后对多次EMD所得IMF分量求平均以消除加入噪声影响，可有效减少模态混叠问题，其具体分解步骤参见文献[10]。

2.2 振动信号的EEMD重构

本文引入峭度准则[11]作为敏感IMF分量选取的基准。选取若干峭度值较大的IMF分量进行重构

(6)

式中Xrms为离散化均方根值;N为采样点数;x(i)为离散化的时频分量信号。

2.3 TKEO瞬时能量提取

对于连续信号x(t)，TKEO表达式为

(7)

而对于离散信号x(n)，可用离散差分方程代替连续时间量的导数，得离散信号x(n)的TKEO表达式如下

ψd[x(n)]=x2(n)-x(n-1)x(n+1)

(8)

本文将其用于计算轴承故障信息的瞬时能量，此方法可突显故障冲击特征，

3 基于敏感SVD和EEMD的故障诊断方法

1)以固定的采样频率fs分别对滚动轴承正常状态、外圈故障及内圈故障状态下的振动信号进行采样；

2)基于采样信号X构建m=2的Hankel矩阵A，对其进行SVD分析，得奇异值矩阵S1=[diag(σ1, …,σm-1)O]，并求解奇异值贡献率N1=[η1,…,ηm-1]；

3)令m=m+1，重复执行步骤(2)，得奇异值贡献率Nm-1，若Nk至Nm-1中总有ηk小于某一特定值η(本文取η=2 %)，则循环结束，并由此确定m=k；否则,重复执行本步骤，直至满足循环结束条件；

4)对已确定维数的分析矩阵进行SVD与重构，得到若干SVD分量信号，通过敏感因子判别其所包含故障成分的多少，并构建敏感因子差分谱，据此自适应选择敏感SVD分量；

5)利用定位因子定位所选敏感SVD分量对应的奇异值，并对其进行有序排列，据此奇异值序列重构信号，以降低背景噪声影响；

6)对降噪信号进行EEMD，得到若干IMF分量和一个趋势分量；

7)计算每个IMF分量的峭度值，根据其大小选择若干(本文取前4个)峭度值较大的分量信号进行重构，以提取局部冲击信息；

8)采用TKEO计算冲击信息的瞬时能量，并对其进行频谱分析。

通过以上步骤，即可有效获取故障特征频率识别轴承早期微弱故障类型。

4 应用与分析

4.1 实验应用

实验采用美国凯斯西储大学电气工程实验室数据[12]对本文所提方法的实用性及有效性进行验证，轴承参数详见表1，其中轴承负载2.237 kW，转频1730 r/min，采样频率为48 kHz。在轴承内圈、外圈上各加工直径为0.177 8 mm，深0.279 4 mm的小槽模拟轴承内圈、外圈局部裂纹故障。

表1 6205—2RS JEM SKF型轴承参数

根据轴承振动理论，计算得轴承内圈故障基频fi=156.14 Hz；外圈故障基频fo=103.36 Hz。

4.2 实验分析

实验分别对轴承内圈故障、外圈故障状态下的振动信号进行了分析，验证本文算法的实用性与有效性。

首先将本文方法应用于轴承内圈故障信号的检测，采用敏感SVD方法对时域振动信号进行分析，根据奇异值贡献率自适应确定Hankel矩阵维数，其曲线如图1(a)所示，当m≥6时，高于m阶的奇异值均趋近于零，其贡献率小于本文所设阈值(2 %)，由此确定m=6作为构建SVD分析矩阵的行数；敏感SVD分析所得分量信号如图1(b)所示，由图可以看出：分量信号3～6的冲击特征更为明显；对所得分量信号进行敏感度评估，敏感因子及其差分谱如图1(c)所示，根据敏感因子差分谱准则，自适应选择前4个SVD分量作为敏感分量；由于敏感因子从大到小排列打乱了奇异值顺序，故本文通过定位因子来确定这4个分量信号所对应的奇异值，定位因子图谱如图1(d)所示，可见敏感分量所对应奇异值在原序列中的位置为3，4，5，6，因此，选择后4个奇异值进行信号重构，以滤除噪声干扰，重构信号如图1(e)所示；对降噪信号进行EEMD，得到9阶IMF分量及一个残余分量，受篇幅限制，本文仅给出前4阶IMF分量如图2(a)所示；计算每个IMF分量的峭度指标，其值大小如表2所示；基于峭度准则选取前4个峭度值较大的IMF分量进行重构，将低频光滑信息从降噪信号中剥离，实现局部微弱故障信息的有效提取，并通过TKEO计算其瞬时能量，进而对其进行频谱分析，频谱图如图2(b)所示，图中清晰定位到了内圈故障的基频(与理论值156.14 Hz较为接近)及倍频(有效定位至4倍频)，因此，可准确判别轴承处于内圈故障状态。

表2 内圈故障IMF分量的峭度指标

图1 内圈故障信号的敏感SVD分析结果

图2 内圈故障信号的特征提取结果

采用敏感SVD方法对轴承外圈振动信号进行分析，根据奇异值贡献率自适应确定Hankel矩阵维数，当m≥6时，随着m值的增大，奇异值均趋近于零，奇异值贡献率小于本文所设阈值(2 %)，其曲线如图3(a)所示，因此，可取m=6作为构建SVD分析矩阵的维数；敏感SVD分析所得分量信号如图3(b)所示，由图可以看出分量信号4～6的冲击特征更加明显；对所得分量信号进行敏感度评估，敏感因子及其差分谱如图3(c)所示，根据敏感因子差分谱准则，自适应选取前4个分量作为敏感分量；由于敏感因子从大到小排列打乱了奇异值顺序，本文通过定位因子定位所选四个分量信号所对应的奇异值，定位因子图谱如图3(d)所示，由图可知，敏感SVD分量信号所对应奇异值在原序列中的位置为3，4，5，6，因此,选择后4个奇异值进行信号重构，以滤除噪声干扰，重构信号如图3(e)所示；对降噪信号进行EEMD，得到8阶IMF分量及一个残余分量，篇幅限制，本文仅给出前4阶IMF分量如图4(a)所示；计算每个IMF分量的峭度指标，其值大小如表3；基于峭度准则选取前4个峭度值较大的IMF分量进行重构，将低频光滑信息从降噪信号中剥离，实现局部微弱故障信息的有效提取，并通过TKEO计算其瞬时能量，进而对其进行频谱分析，频谱图如图4(b)所示，图中清晰定位到了外圈故障的基频(与理论值103.36 Hz较为接近)及倍频(图中仅列至8倍频)，可准确判别轴承处于外圈故障状态。

表3 外圈故障IMF分量的峭度指标

图3 外圈故障信号的敏感SVD分析结果

图4 外圈故障信号的特征提取结果

5 结束语

1)提出敏感SVD方法，通过敏感因子选取故障敏感SVD分量，并基于定位因子定位相应奇异值用于信号重构，从而有效滤除背景噪声干扰，凸显原始振动信号特征。

2)采用EEMD方法对降噪信号进行处理，将其分解为若干从高频到低频有序排列的IMF分量，以有效反映振动信号局部特征；在此基础上，引入峭度准则用于选取敏感IMF分量进行重构，可有效将光滑信息从降噪信号中剥离。

3)将敏感SVD方法与EEMD方法结合起来用于轴承故障诊断，实验证明本文方法可有效提取故障冲击特征频率，从而识别轴承早期微弱故障类型。

[1] Ye Tian,Jian Ma,Chen Lu,et al.Rolling bearing fault diagnosis under variable conditions using LMD—SVD and extreme learning machine[J].Mechanism and Machine Theory,2015,50(90):175-186.

[2] 赵学智，叶邦彦，陈统坚．奇异值差分谱理论及其在车床主轴箱故障诊断中的应用[J]．机械工程学报，2010，46(1)：100-108．

[3] 赵学智，叶邦彦，陈统坚．基于奇异值曲率谱的有效奇异值选择[J]．华南理工大学学报：自然科学版，2010，38(6)：11-18, 23．

[4] 耿宇斌，赵学智．基于Molet小波变换与SVD的故障特征提取[J]．华南理工大学学报：自然科学版，2014，42(7)：55-61．

[5] 王建国，李 健，万旭东．基于奇异值分解和局域均值分解的滚动轴承故障特征提取方法[J]．机械工程学报，2015，51(3)：104-110．

[6] 丁国军，王立德，申 萍，等．基于EEMD能量熵和LSSVM的传感器故障诊断[J]．传感器与微系统，2013，32(7)：22-25．

[7] Jiang Huiming，Chen Jin,Dong Guangming,et al.Study on Hankel matrix-based SVD and its application in rolling element bea-ring fault diagnosis[J].Mechanical Systems and Signal Proces-sing,2015,53:338-359.

[8] 赵学智，叶邦彦，陈统坚．矩阵构造对奇异值分解信号处理效果的影响[J]．华南理工大学学报：自然科学版，2008，36(9)：86-93．

[9] 雷亚国．基于改进Hilbert-Huang变换的机械故障诊断[J]．机械工程学报，2011，47(5)：71-77．

[10] Wu Z H,Huang N E.Ensemble empirical mode decomposition:A noise-assisted data analysis method[J].Advances in Adaptive Data Analysis,2009,1(1):l-41.

[11] 吴小涛，杨 锰，袁晓辉，等．基于峭度准则EEMD及改进形态滤波方法的轴承故障诊断[J]．振动与冲击，2015，34(2)：38-44．

[12] Case Western Reserve University Bearing Data Center.Bearing data center fault test data[EB/OL].[2009—10—01].http:∥www.eecs.case.edu/laboratory/bearing.