基于Laguerre基函数的液位传感器温度补偿方法*

陈韦名，曾喆昭，廖震中，毛亚珍

(长沙理工大学 电气与信息工程学院，湖南 长沙 410076)

0 引 言

为了解决温度对磁致伸缩液位传感器的非线性影响，国内外已从硬件和软件补尝两方面做了大量研究工作[1～5]。由于电子元器件受温度漂移等因素影响，使得测量系统可靠性差、精度低，难以实现全程补偿，因而硬件补偿方法在实际应用过程受到限制。现有软件补偿方法主要包括：多维回归分析法[6]、基于反向传播(back propagation,BP)神经网络的湿度传感器温度补偿方法[7]、基于径向基函数(radial basis function,RBF)神经网络与最小二乘(least square,LS)相结合的融合算法实现湿度传感器的温度补偿方法[8]、基于三次样条插值的温度补偿方法[9]、最小二乘支持向量机(LS-SVM)的温度补偿方法[10]以及基于自适应神经模糊推理系统(adaptive neural-fuzzy inference system,ANFIS)的温度补偿方法等[11]。上述方法尽管均具有一定的温度补偿效果，然而温度补偿精度欠佳、计算量较大。为此，本文提出了一种基于Laguerre基函数曲线拟合的液位非线性校正与温度补偿的新方法，构建基于Laguerre基函数的复合曲线模型拟合液位传感器在各种环境温度时所有标定点下的液位值，并使用递推最小二乘法优化计算复合拟合曲线模型的待定参数，从而实现了在各种环境温度时将液位测量值与环境温度值作为自变量，通过已拟合的Laguerre基函数曲线模型实现液位非线性校正和温度补偿功能，获得了相应环境温度时的液位补偿值。

1 Laguerre基函数曲线拟合模型

1.1 Laguerre基函数定义

当x∈[0,∞)时，Laguerre多项式定义为

Ln+1(x)=(2n-1-x)Ln(x)-(n-1)2Ln-1(x),

n=2,3,…

(1)

式中L1(x)=1;L2(x)=1-x。

1.2 液位传感器的液位温度复合补偿模型

为了便于比较分析，取文献[11]中表1所示的6组对样本数据进行液位温度复合补偿模型建模，如表1所示。令xk为液位测量值(mm)，ydk为液位真值(mm)，tk为环境温度值(℃)。

以表1中tk和xk作为非线性复合校正模型的输入，以y(xk,tk)作为非线性复合校正模型的输出，以液位真值ydk作为拟合样本数据，则基于Laguerre基函数曲线拟合的非线性复合校正模型可表示为

(2)

式中aj与bj为复合拟合曲线的模型参数。为了便于分析，设W=[a0,a1,…,an,b0,b1,…,bm]T，L(k:)=[1,L2(xk),…,Ln(xk),1,L2(tk),…,Lm(tk)]，式(2)可改写为

y(xk,tk)=L(k,:)W

(3)

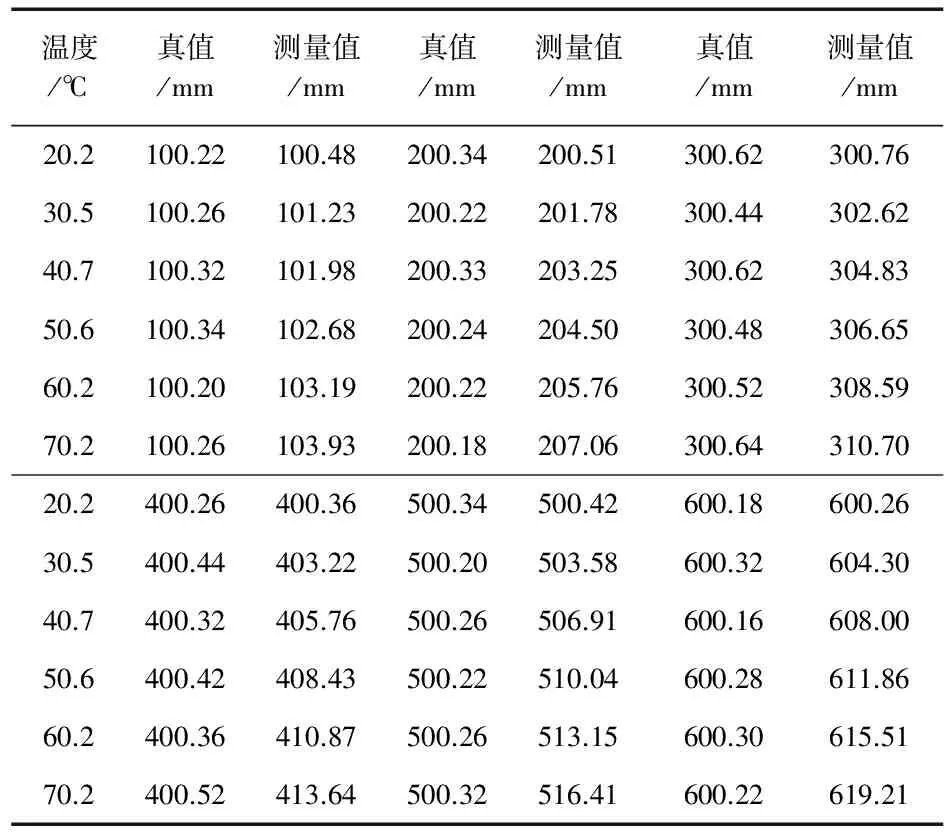
表1 温度补偿前的实验数据

1.3 模型参数更新算法

利用式(3)对表1所示的液位真值数据进行拟合，以获得最优拟合模型参数。设液位与温度非线性补偿误差为

e(k)=ydk-y(xk,tk)

(4)

式中ydk为表1所示的某组对样本数据的第k个液位真值。定义性能指标为

(5)

为了使性能指标J最小，采用基本递推最小二乘法确定模型参数向量W，具体算法描述如下[12]

(6)

Wk+1=Wk+Qke(k)

(7)

Pk+1=[I-QkL(k,:)]Pk

(8)

式中 初始协方差阵P0=αI∈R(n+m)×(n+m);α=103～108。

根据式(4)～式(8)对表1所示的某组对所有样本数据进行迭代训练后，可以获得一组最优的多项式模型参数，使式(2)所示的基于Laguerre基函数拟合曲线模型逼近表1所示的某组对在所有标定点的真值，从而根据获得的最优拟合模型在相应组对范围内的任意温度和液位测量值进行非线性补偿，以实现温度和液位的复合补偿要求。

2 仿真实验

为了验证本文方法的有效性，以文献[19]中表1所示的6组测量数据作为实验对象，下列仿真实验中，取α=106，n=m=7。

1)以表1中的第1组对数据作为仿真对象，仿真结果如表2所示, 最大相对误差小于(3.494 2×10-8)%。

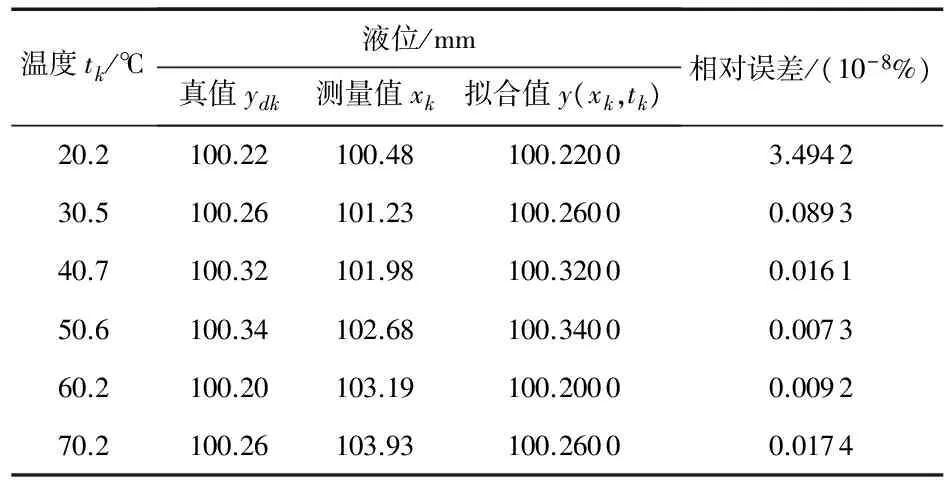
表2 第1组对样本数据及其补偿结果

2)以表1中的第2组对数据作为仿真对象，仿真结果如表3所示,最大相对误差小于(1.237 3×10-7)%。

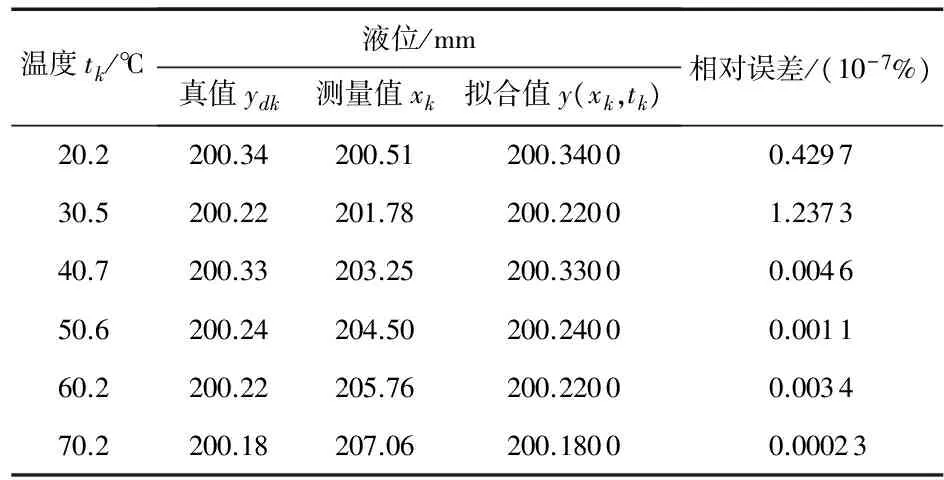
表3 第2组样本数据及其补偿结果

3)以表1中的第3组对数据作为仿真对象，仿真结果分别如表4所示，最大相对误差小于(3.335 1×10-7)%。

4) 以表1中的第4组对数据作为仿真对象，仿真结果如表5所示。最大相对误差小于(3.414 5×10-7)%。

5)以表1中的第5组对数据作为仿真对象，仿真结果如表6所示，最大相对误差小于(1.842 5×10-8)%。

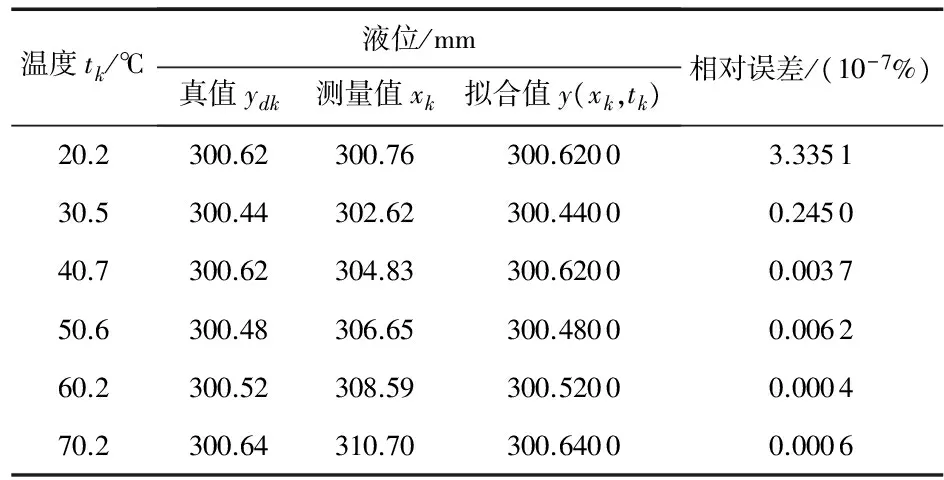
表4 第3组样本数据及其补偿结果

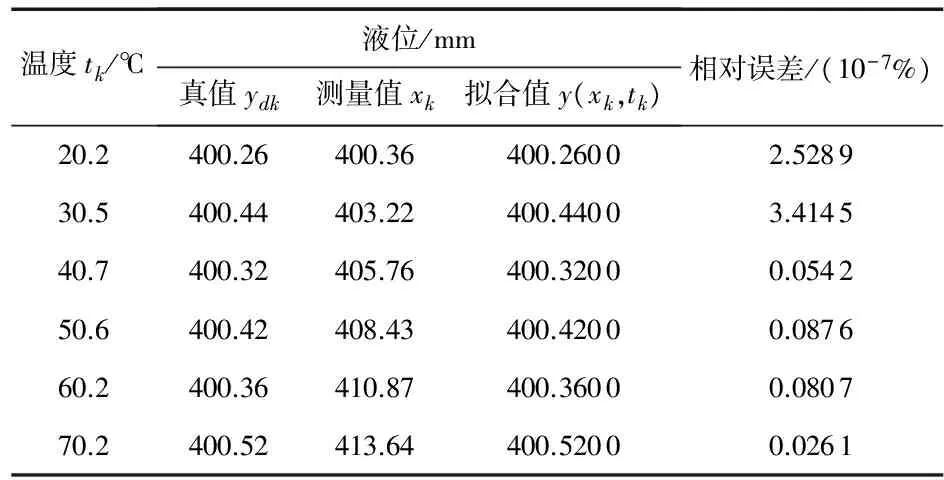
表5 第4组样本数据及其补偿结果

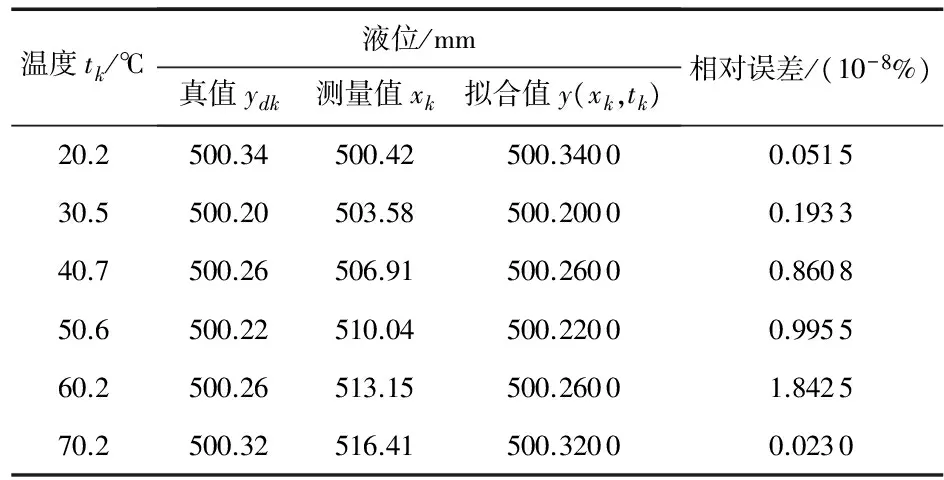
表6 第5组样本数据及其补偿结果

6)以表1中的第6组对数据作为仿真对象，仿真结果如表7所示，最大相对误差小于(1.479 0×10-7)%。

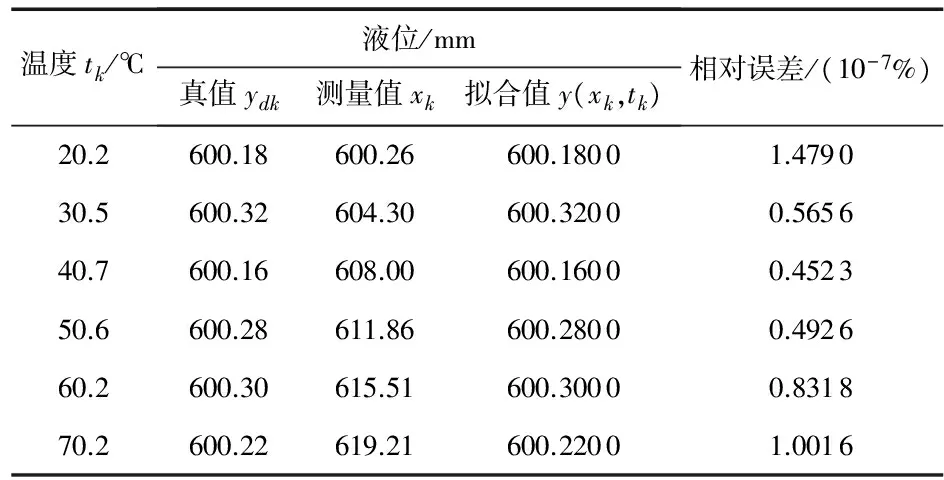
表7 第6组样本数据及其补偿结果

3 结 论

提出了基于Laguerre基函数的液位传感器温度与液位复合补偿模型，使用递推最小二乘法对Laguerre基函数复合曲线模型参数进行了优化计算。6个仿真实验的结果表明：温度与液位的优化曲线模型完整刻画了液位传感器的温度—液位特性的函数关系，根据被测的液位和环境温度即可高精度计算出液位传感器的实际液位值，最大相对误差小于(3.414 5×10-7)%，而文献[11]的最大相对误差为0.88 %。与文献[11]相比，本文方法的温度补偿精度提高了近千万倍，为液位测量领域的温度和液位非线性校正提供了良好的理论方法。

[1] 周庆飞，徐明龙.具有温度自补偿功能的高分辨力倾角传感器的设计[J].传感器与微系统，2012，31(1)：107-110.

[2] 于 娜，刘志远，赵佳龙.倾角传感器的温度补偿研究[J].传感器与微系统，2014，33(10):14-16.

[3] 何 刚，高国伟，潘宏生，等.反正弦法倾角传感器温度补偿研究[J].传感器与微系统，2016，35(5):13-15.

[4] 王增跃,李孟委,刘国文.硅微加速度计温度特性分析与误差补偿[J].传感器与微系统，2016，35(1):25-28.

[5] 赵 斌，王建华.基于PSO-BP的红外温度传感器环境温度补偿[J].传感器与微系统，2015，34(2):47-49.

[6] 孙德敏,张 利,王 永,等.基于乘积型最小二乘法的传感器特性拟合[J].传感技术学报,2002(4):293-297.

[7] 卢智远,周永军,李卫军.传感器非线性误差校正的BP神经网络方法研究[J].传感器技术,2005,24(2):11-12.

[8] 行鸿彦,彭基伟,吕文华,等.一种湿度传感器温度补偿的融合算法[J].传感技术学报，2012,25(12):1711-1716.

[9] 江 东,单 薏,刘绪坤,等.函数拟合法力数字传感器的非线性和温度补偿[J].传感器与微系统,2016,35(2):16-19.

[10] 辛守乔,肖立业,马玉鹏.巨磁阻传感器输出非线性与温漂的补偿[J].高电压技术,2013,39(5):1178-1183.

[11] 谢 苗,刘治翔,毛 君.基于改进型ANFIS的磁致伸缩液位传感器温度补偿[J].传感技术学报,2015,28(1):49-56.

[12] 曾喆昭，黄创霞，周富照.数值计算方法与应用[M].北京：科学出版社，2013.