PMMA在类固态微热压印过程中冷却速率与松弛速率的规律分析

李 瑞，吴大鸣,*，王 琦，刘 颖，孙靖尧，曹亚楠

(1.北京化工大学机电工程学院，北京 100029；2.有机无机复合材料国家重点实验室，北京 100029)

0 前言

在传统热压工艺中，无定形聚合物的理想加工T是黏流温度(Tf)以上，此时聚合物处于熔融状态，极易充模成型，但因其压印周期长[1-3]，迄今为止并没有得到广泛的商业应用。玻璃化转变温度(Tg)附近的聚合物也具备足够的加工性能，北京化工大学吴大鸣教授团队提出了“类固态”的概念以及“预热式”与“非预热式”2种新的工艺[4-7]，大大提高了成型效率。类固态是指被压印聚合物处于Tg(无定形聚合物)或热变形T(结晶型聚合物)附近的非流动状态。这种状态下聚合物处于玻璃态向橡胶态转化的过程中，会“软化”，也具备弹塑性，聚合物快速、小形变的应力应变关系非常复杂，同时，加工T远低于Tf，内应力在保压和脱模过程中如果没有得到充分松弛，则直接影响微纳结构的几何稳定性，所以研究聚合物应力松弛特性与制件降温冷却过程中v(t)的关系，可以合理地确定保压时间和脱模v(t)，将压印制件的内应力降到较低水平，从而保证制件微纳结构的几何稳定性。

许多研究学者也对微热压印工艺中的应力松弛及降温冷却过程对微结构制件品质的影响开展过研究。Kakumani[8]针对于PMMA的应力松弛过程，特别是大应变条件下的应力松弛现象进行了大量的实验研究。Mathiesen 和Vogtmann 等[9]则依据PMMA应变行为特征，建立了适用于PMMA材料的跨Tg的由弹簧、黏壶以及交互网络构成的新型黏弹性模型。Hardt 和Ganesan 等[10]设计了一套用于微热压印实验的装置，分析了微热压印过程中包括v(t)在内的各个实验条件对聚合物材料变形过程的影响及产生原因。Liu和Li等[11]通过光学体视显微镜(SLM)系统记录的方式对微热压印过程中聚合物的变形行为进行了对比和分析。但是在类固态微热压印过程中，v(t)的高低对微纳制件松弛过程的快慢造成影响的相关研究较少。本文在不同T下进行了应力松弛实验，建立了p-T指数模型和σΔ(t)-v(t)模型，并用自行研制的热压印机进行了不同v(t)下prism微结构的类固态微热压印实验来验证模型的实用性。

1 PMMA的p-T指数模型的建立

1.1 p的表征

随着T的变化，聚合物的应力松弛过程也会发生变化。对不同T下的聚合物而言，其应力松弛过程的快慢可用p来表征，p的宏观意义为在T不变的条件下，单位时间内聚合物平均内应力松弛量的变化率。聚合物在不同T下具有不同的τ值，τ的宏观意义为聚合物的内应力降低到其初始应力σ0的e-1倍(即为0.368倍)时所需要的时间[12]。如式(1)所示，利用τ对p进行求取。

(1)

式中p——松弛速率，s-1

τ——松弛时间常数，s

1.2 不同T下聚合物的p的求取

1.2.1 实验条件

当外界T变化时，对聚合物的应力松弛过程也会产生不同程度的影响。本实验的目的在于探究不同T对聚合物应力松弛过程的具体影响，并通过对实验数据的处理和分析，选取合适的数学模型对该影响进行定量描述。

实验材料选用德国盖尔公司生产的透明PMMA片材，试样尺寸为10.0 mm×10.0 mm×3.0 mm。实验设备选用添加了加热模块以及数据提取模块的东莞智取精密仪器有限公司生产的PT-880小型拉压力机。为保证PMMA试样的T能够满足实验要求，实验前均使用巩义市予华仪器有限公司生产的DZF-6050型真空干燥箱对试样进行15 min的保温加热。

实验过程中设定的加载压力为3.0 MPa，加载速率为30.0 mm/min[13]。PMMA试样的保温加热作业所选取的T区间为：

(1)处于PMMA的Tg以下，在30～105 ℃内，依次选取T为30、40、50、60、65、70、75、80、85、90、95、98、101、104 ℃进行实验；

(2)处于PMMA的Tg以上，在105～130 ℃内，依次选取T为107、110、112、114、116、118、120、122、124、126、128、130 ℃进行实验。

由于聚合物的应力松弛现象符合时温等效原理，并且相对于时间因素而言，聚合物的应力松弛过程受T的影响更加明显，因此，相比于Tg以下的T区间，在Tg以上的范围所选取的实验T间隔较小。

1.2.2 实验过程

在PMMA试样应力松弛的实验过程中，由于加载压力的影响，试样会发生一定程度的变形。但是加载压力的数值以及试样的尺寸均较小，所以试样自身所产生的变形量也较小，因此可以假设试样的截面面积(S)在实验过程中保持不变，即PMMA试样在不同时刻的松弛模量E(t)可以用式(2)表示：

(2)

式中t——时间，s

E(t)——t时刻PMMA试样的松弛模量，N/m

F(t)——PMMA试样在t时刻加载压力的大小，N

S——试样在加载方向上的截面面积，m2

ε——试样在加载压力为3.0 MPa时所产生的应变量大小

根据实验所测得的处于不同T下PMMA试样的τ值以及式(2)，可以对不同T下PMMA试样的p进行计算，结果如图1所示。

图1 不同T下PMMA试样的τ和pFig.1 Relaxation time constant and relaxation rate of PMMA specimen at different temperature

1.3 p-T指数模型的建立

如式(3)所示，通过对实验结果的计算和整理，得到不同T下PMMA试样的p之后，建立起聚合物的p-T指数模型，便于对不同T下聚合物的τ和p进行计算和分析。

(3)

式中p——不同T下PMMA的松弛速率，s-1

T——温度，K

C——常数

αi——自然对数e所对应的系数

βi——外界T所对应的系数

N——拟合级数

图2 PMMA的p-T变化拟合曲线Fig.2 p-T fitting curve of PMMA

通常情况下N越大，所建立的指数模型同实验曲线的重合度也就越高，选取N=3，利用式(3)中的p-T指数模型进行非线性拟合，如图2所示。最终得到PMMA的p-T指数模型同实验曲线之间的拟合度达到了0.98，满足使用要求，其指数模型中各个参数的数值如表1所示。

表1 PMMA的p-T指数模型参数表Tab.1 p-T index model of PMMA parameter table

将PMMA的p-T指数模型参数表中的各个参数带入到式(3)中，可以得到式(4)。

p= -0.00699+(1.45263×10-9e0.04293T+

7.33807×10-5e0.01792T-

8.21193×10-6e0.02378T)

(4)

由此，完成了对PMMA的p-T指数模型的构建，利用此模型可以对处于不同T下PMMA的p和τ进行计算。

2 PMMA的σΔ(t)-v(t)模型的建立

在实际的类固态微热压印脱模过程中，微结构制件具有一定的v(t)，因此p-T指数模型并不能够实现真正意义上的连续求解。所以还要将聚合物的应力松弛过程同其冷却过程相结合，找到它们之间的关系，再以积分的形式建立起可以连续求解的聚合物σΔ(t)-v(t)模型。

如图3所示，在聚合物类固态微热压印的工艺中，聚合物制品降温冷却的过程就是由T1降低至T2的过程。设定聚合物制件由T1冷却到T2的过程中所消耗的时间为Δt，则v(t)可由式(5)表示。

(5)

式中 dT——在图2横坐标T上所选取的微元

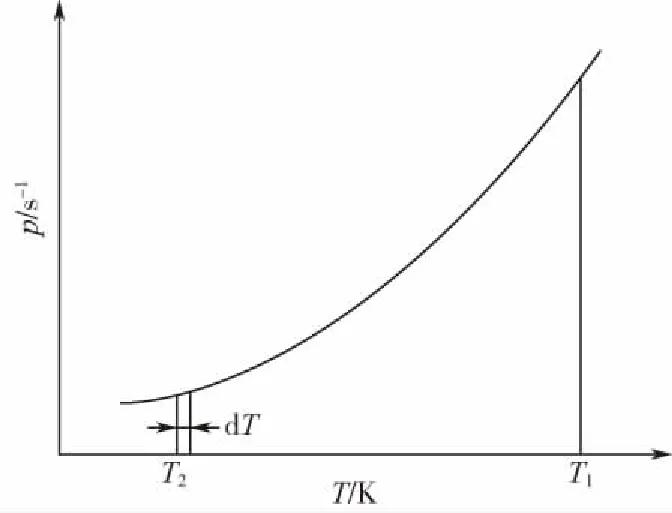
图3 聚合物的p随T变化的情况示意图Fig.3 Variation of polymer relaxation rate with temperature

dt——在图4横坐标t上所选取的微元

假设聚合物制件的冷却过程是匀速的，则v(t)可用式(6)表示。

(6)

定义σΔ(t)为对一定t范围内聚合物材料的实时内应力相对于初始应力的变化率。根据定义，聚合物的σΔ(t)可用式(7)表示。

(7)

式中σ(t)——聚合物在t时刻内应力的大小，N/m

σ0——聚合物初始应力的大小，N/m

如图4所示，在类固态微热压印的工艺中，对于一定t范围内的降温冷却过程，即从t1时刻到t2时刻，如式(8)所示通过对聚合物的p进行积分的方法来对其σΔ(t)进行求取。

(8)

图4 聚合物的p随t变化的情况示意图Fig.4 Variation of polymer relaxation rate with time

将式(5)进行变换可得到式(9)。

(9)

再将式(9)代入到式(8)，其中由于图2所示聚合物制件由T1冷却至T2的过程，正是图4所示的t1时刻到t2时刻的降温过程，因此在整个体系降温冷却的过程中，T和t之间存在着一一对应的映射关系，用T对t进行等效替换后，聚合物的σΔ(T)可用式(10)表示。

(10)

假定聚合物制件的冷却过程是匀速的，则将式(6)代入到式(10)可以得到式(11)。

(11)

式(11)表示的是在已知聚合物不同T、p的条件下，当聚合物从T1以v(t)降低到T2时，聚合物σΔ(T)的计算过程，最后将式(3)代入可以得到式(12)。

(12)

至此完成了PMMA的σΔ(t)-v(t)模型的建立。利用该模型，在类固态微热压印降温冷却的过程中，若是已知初始T、最终T以及冷却t，便可以对聚合物制件的σΔ(t)进行计算求解。

将式(7)进行变换，同时使用T对t进行等效替代，并将式(12)代入，如式(13)所示便可对降温冷却过程中聚合物的残余应力[σ(T)]进行求解。

σ(T)=σΔ(T)×σ0

(13)

同样的，对于除了PMMA以外的其他类型的聚合物，均可以用上述方法构建其相应的p-T指数模型以及σΔ(t)-v(t)模型。对不同聚合物选取相应的计算模型进行相关的实验分析和定量讨论，这对于类固态微热压印工艺的优化和改善具有十分重要的推动作用。

3 prism微结构类固态等温热压印实验

通过实验分析脱模v(t)与σΔ(t)以及微结构复制率之间的关系，材料选用德国盖尔公司生产的透明PMMA片材，试样尺寸为40.0 mm×40.0 mm×5.0 mm。设备采用北京化工大学自制的微纳热压印实验装置[14-15]和特征尺寸为49 μm的prism模具(图5、图6)，对Tg为105 ℃的PMMA基片，模具T为110 ℃，压印压力为5 MPa，保压t为20 s。保证其他工艺条件不变，制件T从110 ℃降到30 ℃，v(t)分别设定为50、60、70、80、90、100 ℃/min，并记作1#～6#样品。

图5 微压印装置Fig.5 Device of micro-hot embossing

图6 Prism模具的截面照片Fig.6 Picture of prism die section

取N=3，将6个v(t)和表2中的数据代入到式(12)，得到如图7所示的σΔ(t)。

可以看出，随着v(t)的提高，σΔ(t)越来越小，说明内应力松弛的更加充分，相应微结构的成型精度越高，将制品在中国东莞万通仪器有限公司生产的JTVMS-1510T 3D图像测量系统下观察结果如图8所示，并计算复制率。

每个样品各选取8个prism微结构，测量其尺寸，其中L为槽间距，H为槽深，A为角度。分别计算其均值后，与模具尺寸作比较，取(结果-100 %)的绝对值较大者作为复制率，结果如表2所示。

图7 不同v(t)条件下的σΔ(t)Fig.7 Stress change rates at different cooling rates

样品：(a)1# (b)2# (c)3# (d)4# (e)5# (f)6#图8 样品的微压印结构图Fig.8 Aremicro-embossed structure photos of the samples

表2 样品的微结构平均尺寸与复制率Tab.2 Microstructure average size and copy rates of the samples

注：L0、H0、A0分别为模具微结构中的槽间距、槽深和角度，其中L0=49 μm、H0=24 μm、A0=90.727 (°)。

图9 110 ℃下，5 h后的prism微结构图Fig.9 Prism microstructure photo after 5 h at 110 ℃

通过prism微结构实验，发现v(t)从50 ℃/min提高至80 ℃/min的过程中，复制率不断提高，与理论模型得到的随着v(t)的提高，内应力松弛更加充分的结论相匹配，从而验证了σΔ(t)-v(t)模型的实用性。而从80 ℃/min提高至100 ℃/min的过程中，复制率变化不大，原因是成型精度已经很高，仅仅改变v(t)很难再提高复制率，要想继续提高复制率，还需综合考虑类固态微热压印工艺。为了考察微压印结构的几何稳定性，将5#样品置于110 ℃烘箱内5 h，如图9所示，没有发现微结构产生视觉可见的几何变化。

4 结论

(1)基于无定形聚合物PMMA不同T下的应力松弛实验，建立了p-T指数模型，可求取不同T下的p以及τ，进而指导类固态微压印过程中保压t的选取；

(2)建立了聚合物σΔ(t)-v(t)模型，计算得到随着v(t)的提高，σΔ(t)越来越小，内应力松弛的更加充分，微结构的成型精度越高；

(3)观察相应的prism微结构实验，在提高v(t)的过程中，制品的复制率也不断提高，验证了模型的实用性；因此可根据此模型合理选取T、保压t、v(t)等参数，这对类固态微热压印工艺的优化和改善具有十分重要的推动作用。

[1] Yao D, Nagarajan P, Li L, et al. A Two-station Embos-sing Process for Rapid Fabrication of Surface Microstructures on Thermoplastic Polymers[J]. Polymer Enginee-ring & Science, 2007, 47(47):530-539.

[2] Worgull M. Hot Embossing: Theory and Technology of Microreplication[M]. Elsevier, 2009:56-79.

[3] Peng L F, Deng Y J, Yi P Y, et al. Micro Hot Embos-sing of Thermoplastic Polymers: a Review[J]. Journal of Micromechanics and Microengineering, 2014, 24(1):13001-13023.

[4] 杨振洲.聚合物微结构平板热压印成型工艺的研究[D].北京:北京化工大学机电工程学院,2015.

[5] 敬鹏生.聚合物表面微结构平板热压印连续成型工艺及设备的研究[D].北京:北京化工大学机电工程学院, 2014.

[6] 江 冲, 吴大鸣, 刘 颖,等. 等温准热压印中聚合物微结构成型的分析[J]. 高分子材料科学与工程, 2016, 32(10):105-111.

Jiang Chong, Wu Daming, Liu Ying, et al. Forming Analysis of Microstructure in Isothermal Quasi-embossing Conditions[J].Polymer Materials Science & Engineering, 2016, 32(10):105-111.

[7] 孙靖尧,吴大鸣,刘 颖,等.聚合物微纳制造技术[J].橡塑技术与装备,2016,42(10):1-9.

Sun Jingyao, Wu Daming, Liu Ying, et al. Polymer Micro-nano Manufacturing Technology[J]. China Rubber/Plastics Technology and Equipment, 2016,42(10):1-9.

[8] Kakumani A. Stress Relaxation in Polymethyl Methacrylate(PMMA) at Large Strains During the Process of Hot Embossing[D].The United States: The Ohio State University College of Engineering, 2013.

[9] Mathiesen D, Vogtmann D, Dupaix R B. Characterization and Constitutive Modelingof Stress-relaxation Behavior of Polymethyl Methacrylate(PMMA) Across the Glass Transition Temperature[J]. Mechanics of Materials, 2014, 71(5):74-84.

[10] Hardt D E, Ganesan B, Dirckx M, et al. Process Variability in Micro-embossing[J/OL]. Innovation in Manufacturing Systems and Technology(IMST), 2004[2017-06-15]. http://www.researchgate.net/publication/37598102.

[11] Liu C, Li J M, Liu J S, et al. Deformation Behavior of Solid Polymer During Hot Embossing Process[J]. Microelectronic Engineering, 2010, 87(2):200-207.

[12] 金日光，华幼卿. 高分子物理[M]. 化学工业出版社, 1991:189-192.

[13] 王 琦,吴大鸣,刘 颖,等.PMMA近玻璃化转变温度下应力松弛特性分析[J].塑料, 2017,46(2):5-8.

Wang Qi, Wu Daming, Liu Ying,et al.The Analysis of Stress-Strain Behavior of PMMA Near Glass Transition Temperature[J].Plastics, 2017,46(2):5-8.

[14] 敬鹏生, 刘 颖, 许 红,等. 一种聚合物表面微结构平板热压印连续成型的方法[J]. 塑料, 2015, 44(1):83-86.

Jing Pengsheng,Liu Ying,Xu Hong,et al. A New Type of Polymer Extrusion Continuous Plate Embossing Microstructure Forming Method[J].Plastics, 2015, 44(1):83-86.

[15] 吴大鸣,刘 颖,郑秀婷,等.一种快速聚合物微结构等温平板热压印工艺：中国，CN105058770A[P].2015-11-18.