基于结构关系识别的中国汽车销量预测

高 俊 杰, 谢 亚 南, 顾 丰, 于 晗

( 1.大连理工大学 汽车工程学院, 辽宁 大连 116024；2.大连海洋大学 经济管理学院， 辽宁 大连 116023 )

0 引 言

汽车销量预测的精度直接影响对市场供求格局的判断及对企业竞争优势和产品开发类型的确定．准确的汽车销量预测有利于企业制订今后的营销战略和生产计划，已经成为汽车市场竞争中至关重要的环节．

传统的汽车销量预测大都是根据历年的汽车销量数据本身展开．其实，影响汽车销量的因变量众多，时间序列模型因能深入识别各变量时间序列的内在关系，常被用于汽车销量预测．例如：用向量移动平均模型(auto-regressive and moving average model，ARMA)来进行预测[1-2]．但该模型是由其自身的过去或滞后值以及随机扰动项来解释，并未考虑经济变量对汽车销量的影响．而向量自回归模型(vector auto-regression，VAR)不仅可以分析变量彼此关系，还能表达滞后期以及任何期干扰对其他变量产生的影响．在VAR基础上发展而来的向量误差修正模型(vector error correction model，VECM)还能反映变量之间由短期波动向长期均衡演变的动态化过程，确定模型所包含的多个变量间的理论关系．与传统的数理统计和经济计量学方法无法分析非平稳过程生成的时间序列数据相比，VECM可以显示出独特优势[3-5]．因此，本文考虑宏观经济变量的影响，在识别变量间关系的基础上，引入VECM对中国汽车销量进行预测研究．

1 向量误差修正模型

作为一种计量经济学模型，VECM是在VAR的基础上建立的多变量时间序列模型，它的核心思想是：变量之间的协整关系代表了彼此之间的长期均衡关系，而不断调整短期波动可实现此长期均衡关系．

如果在VAR中yt的内生变量都含有单位根，且含有相同的单整阶数，此时可以进行差分来建立一个平稳的VAR模型．但这将会丢失重要的非均衡信息，因此建立纯粹的差分VAR模型并非最佳选择．在变量差分形式构建VAR模型的基础上，将变量之间的长期协整向量作为非均衡误差项，即向量误差修正模型．使yt所包含的k个I(1)序列之间存在协整关系，其误差修正模型的表达式可表示为[6]

(1)

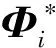
2 数据来源

本文收集了2007年1月至2016年12月的中国汽车总销量的月度数据，数据来源于汽车工业协会．对于宏观经济变量选择，以能更有效率地预测并更好地表达汽车销量与经济变量之间的结构关系为标准．因此，所选择的经济变量应具有以下性质：

(1)能描述汽车消费者支付的价格变化；

(2)能影响汽车工业需求行为；

(3)能代表国民经济和经济周期的变化．

除此以外，还应考虑变量选取中经常出现的过度参数化、多重共线性以及模型设定等问题．基于相关文献和一些初步检测，本文筛选出4种经济变量：95#无铅汽油价格(下文简称汽油价格)、消费者信心指数(CCI)、居民消费指数(CPI)和钢材产量．这些2007年1月至2016年12月间的月度数据来源于东方财富网、国家统计局、中国产业信息网和前瞻网．本文选择2007年1月至2015年12月的数据进行建模，2016年12个月的数据用来检验模型结果．

本文研究中国汽车销量与宏观经济变量之间的动态联系，各个变量的名称、来源和解释等信息如表1所示．

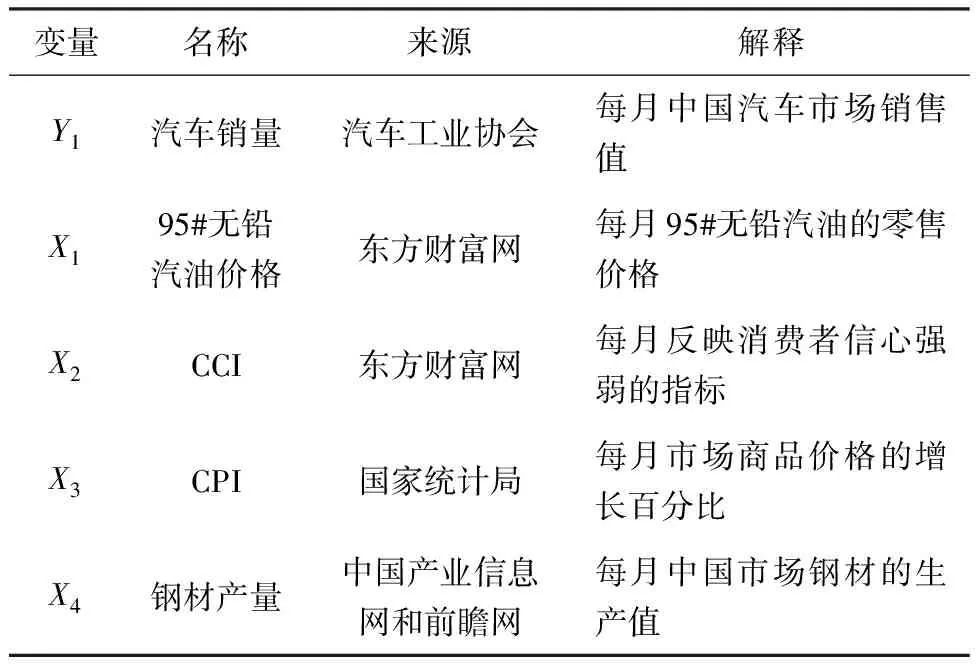
表1 变量概述

3 模型构建

时间序列的统计规律不随时间的推移而变化，只有时间序列是平稳的，才能运用现有的计量经济模型进行分析．因此，在分析时间序列前，须先讨论时间序列的平稳性．结构关系识别过程中，首先，进行单位根检验．若检验结果是平稳的，则导入VAR；否则，进行差分，并以差分形式建立VAR．其次，选取最佳滞后阶数，进而进行弱外生性检验，解决过度参数化问题，确定合理的内生变量之间的结构关系．通过协整检验，分析内生变量之间是否具有长期均衡关系．进一步，通过格兰杰因果检验来判断此关系是否为因果关系．如果内生变量间存在协整关系并具有格兰杰因果关系，则可导入VECM进行预测．

3.1 单位根检验

结构关系识别中的单位根检验用来检查时间序列的平稳性[7]．本文采用常用的时间序列平稳性检验方法，即augmented Dickey-Fuller(ADF)检验[8-9]．ADF的原假设是至少存在一个单位根，备选假设则认为序列不存在单位根．关于最佳的滞后阶数的选择，本文综合赤池信息准则(Akaike information criterion，AIC)以及施瓦茨信息准则(Schwarz criterion，SC)来选取p值[10]．其原则与方法是在选取p值过程中确保AIC与SC尽可能地同时达到最小．用ADF单位根检验对原始数据及其一阶差分分别进行单位根检验．表2检验结果显示每个变量的原始时间序列非平稳且其一阶差分平稳，即各变量的时间序列同为一阶单整，由此说明变量满足VECM构建的要求．

3.2 滞后阶数的选取

由于模型的自由度随着滞后阶数的增大而减少，滞后阶数的选取在确保模型足够自由度的同时又要能全面反映模型动态特征，选取最佳滞后阶数[11]．除了AIC和SC两个检验统计量，关于滞后长度标准，还需要结合连续改进的似然比检验统计量(likelihood ratio，LR)、最终预测误差(final prediction error，FPE)和Hannan-Quinn信息准则(HQ)，如表3所示．

从表3的检验结果得出，根据5个检验统计量选取的所有变量建立的无约束VAR模型的最佳滞后阶数为2，而建立的VECM的最佳滞后阶数等于无约束VAR模型的最佳滞后阶数减1，即为1．

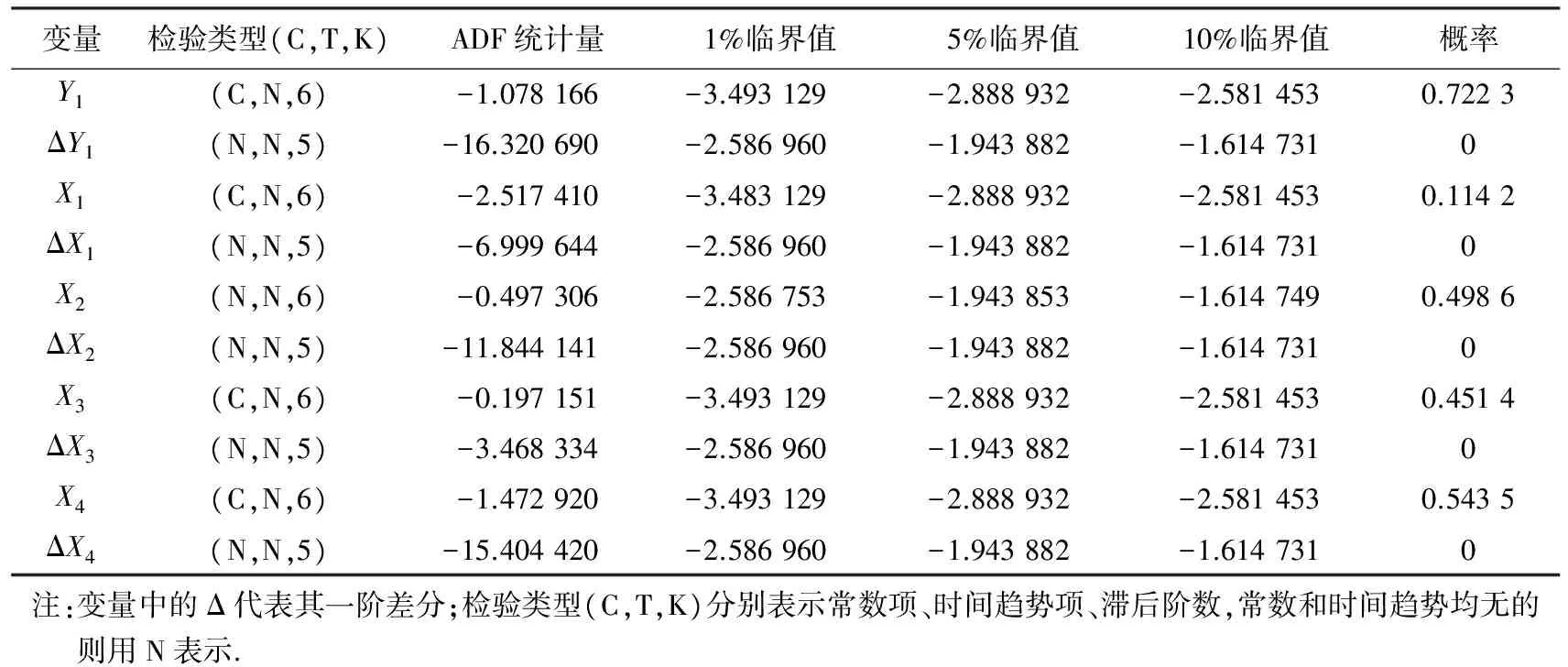
表2 原始变量及其一阶差分的ADF单位根检验

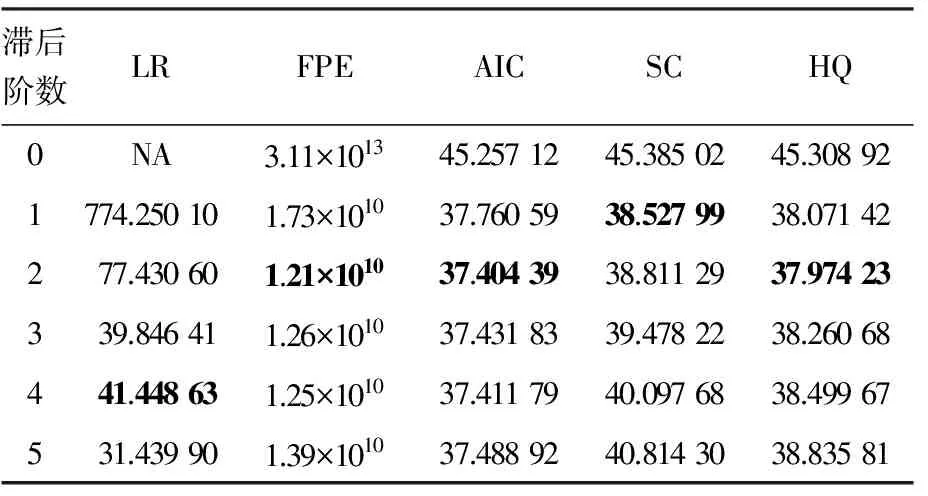
表3 最佳滞后阶数的选取(所有变量)

3.3 格兰杰因果检验

格兰杰因果检验除了可以区别内外生变量外，还能识别变量之间的因果关系．为了检验因果关系，本文采用F统计量和概率来说明．检验结果见表4．当概率小于0.05，则拒绝原假设，也就意味着：存在格兰杰因果关系．

根据检验结果可以构架出关系图(图1)．从图中可以看出，除了CPI和CCI，其余的变量彼此之间均存在格兰杰因果关系．因此初步判断CPI和CCI为外生变量，其余变量为内生变量．

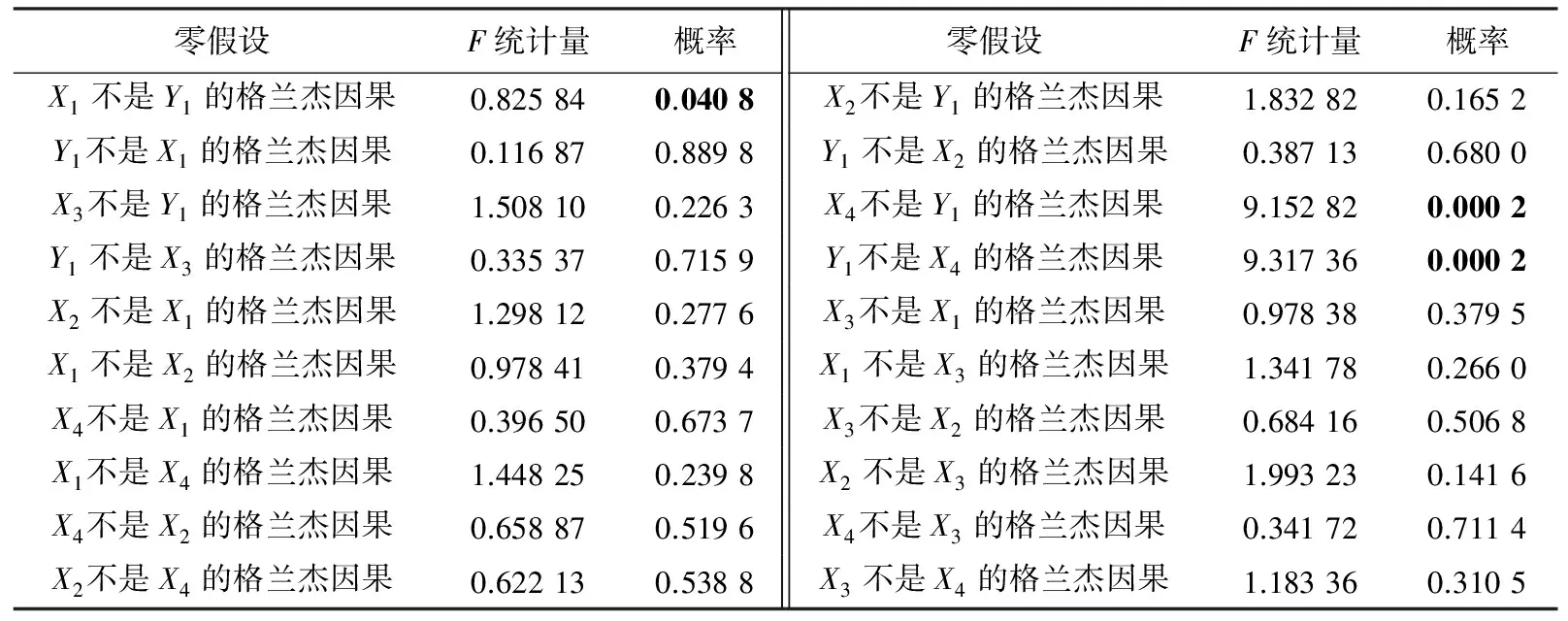
表4 格兰杰因果检验

图1 各变量格兰杰因果检验关系图

3.4 弱外生性检验

弱外生性检验用来区分变量的内外生性，避免外生变量对模型规模的敏感性[12]．弱外生性在建模之后检验，区别于建模之前的格兰杰因果检验．在VAR中进行卡方统计量检测．表5给出具体检验，在5%的显著水平下拒绝虚无假设，即具有因果关系．

表5 弱外生性检验

根据检验的结果可以构架出各变量之间关系图(图2)，可以看出，只有CPI和CCI影响其他变量而不受其余变量的影响．因此，可以确定CPI和CCI是外生变量，这与格兰杰因果检验结果一致．

图2 各变量弱外生性检验关系图

3.5 协整检验

Engle和Granger(1987)表明如果非平稳时间序列之间的线性整合是平稳的，则该时间序列就是协整的[13]．在进行协整检验之前需对所有内生变量确定其最佳滞后阶数，用内生变量建立无约束VAR模型，表6说明其最佳滞后阶数的结果选取为6．因此用内生变量建立的VECM和此次协整检验的最佳滞后阶数同为5．本文的协整检验采用Johansen检验方法[14]．协整检验结果如表7、8所示．从表中可以看出：有协整关系的原假设不能被拒绝，而没有协整关系的原假设被拒绝．因此，变量间存在协整关系．

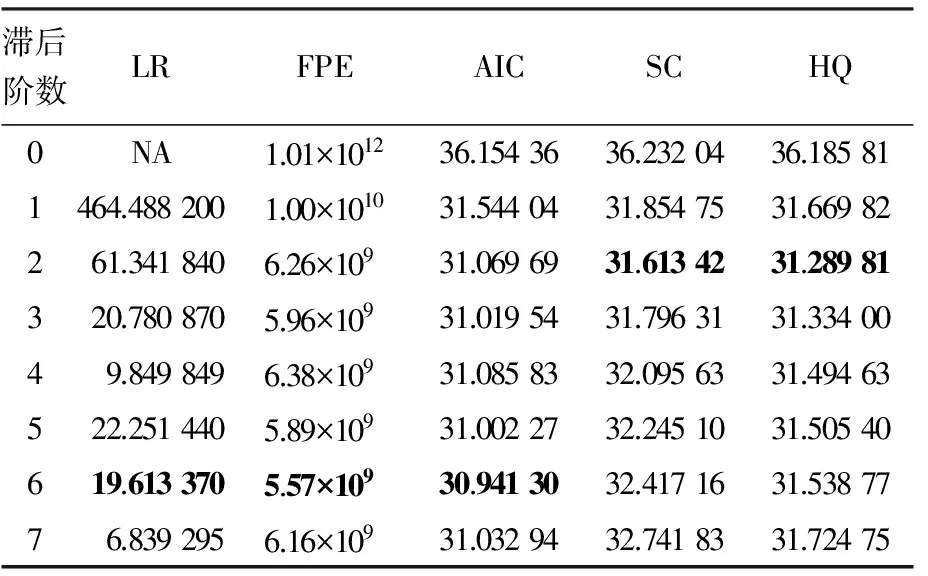
表6 最佳滞后阶数选取(内生变量)

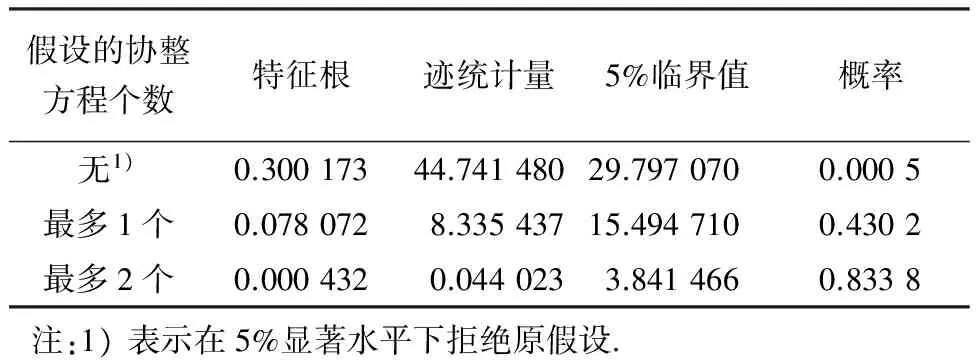
表7 Johansen的协整迹检验

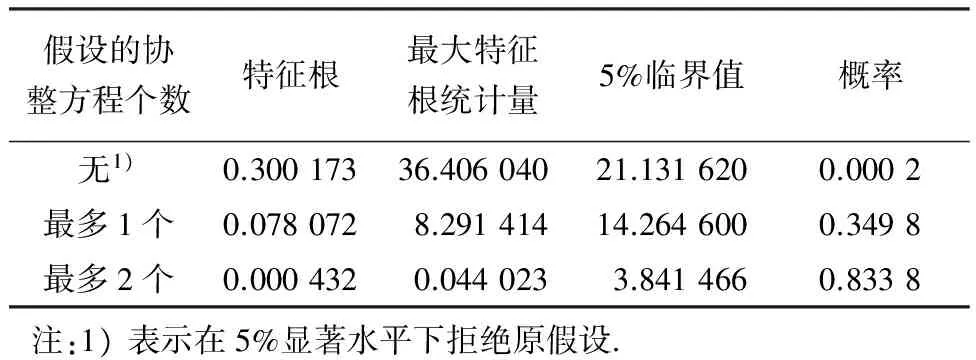
表8 Johansen的协整最大特征根检验

从表中可以看出，内生变量之间存在协整向量关系，说明变量之间存在长期关系，可以构建协整约束的VECM．

表9展示了标准化协整方程系数，将变量之间的协整关系标准化得到协整方程为

Y1=-0.184 733X1+0.026 620X4 (2)

表9 标准化协整方程系数

4 预测性能评估

4.1 预测模型的建立

由共整合检测发现汽车销量与内生经济变量彼此存在共整合关系，因此在应用向量自回归模型分析时应加入误差修正向量，即以向量误差修正模型分析，将各变量的残差值加入估计式[15]．在此基础上，用内生变量分别建立差分形式的VAR和VECM，模型如下：

VAR：

D(Y1)=-0.566 981×D(Y1(-1))-0.111 518×

D(Y1(-2))-0.081 942×D(Y1(-3))-

0.319 023×D(Y1(-4))-0.321 587×

D(Y1(-5))-0.018 142×D(X1(-1))+

0.152 946×D(X1(-2))+0.140 773×

D(X1(-3))-0.411 208×D(X1(-4))+

0.059 164×D(X1(-5))+0.008 835×

D(X4(-1))-0.012 432×D(X4(-2))-

0.012 679×D(X4(-3))-0.012 408×

D(X4(-4))-0.003 031×D(X4(-5))+

5.501 339

(3)

VECM：

D(Y1)=-0.788 328×D(Y1(-1)+0.184 733×

X1(-1)-0.026 620×X4(-1)+

28.065 421)-0.033 573×D(Y1(-1))+

0.340 151×D(Y1(-2))+0.386 321×

D(Y1(-3))+0.152 728×D(Y1(-4))-

0.070 848×D(Y1(-5))+0.267 255×

D(X1(-1))+0.328 637×D(X1(-2))+

0.339 316×D(X1(-3))-0.241 199×

D(X1(-4))+0.189 767×D(X1(-5))-

0.005 401×D(X4(-1))-0.019 899×

D(X4(-2))-0.021 323×D(X4(-3))-

0.022 941×D(X4(-4))-0.012 935×

D(X4(-5))+0.227 362

(4)

4.2 预测模型稳定性检验

在模型进行预测之前有一必备环节，即模型稳定性检验．VAR和VECM的稳定性检验的判定条件为：被估计的VAR和VECM所有根模的倒数均小于1，即都位于单位圆内[14]．VAR和VECM的特征根的个数是p×k，其中内生变量个数相同，即为k，不同的是VAR中的p为一阶差分建立VAR的最佳滞后阶数，而VECM中的p为无约束VAR的最佳滞后阶数．VAR和VECM的平稳性检验结果分别如表10、11所示．

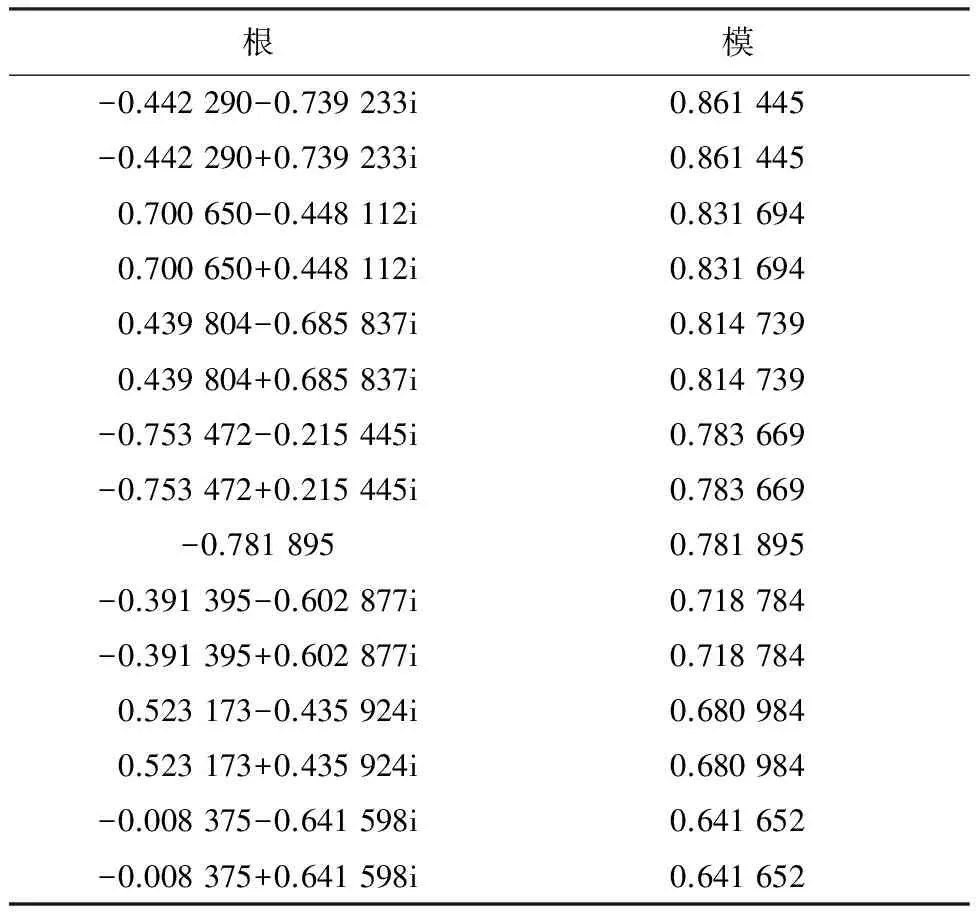
表10 VAR的平稳性检验

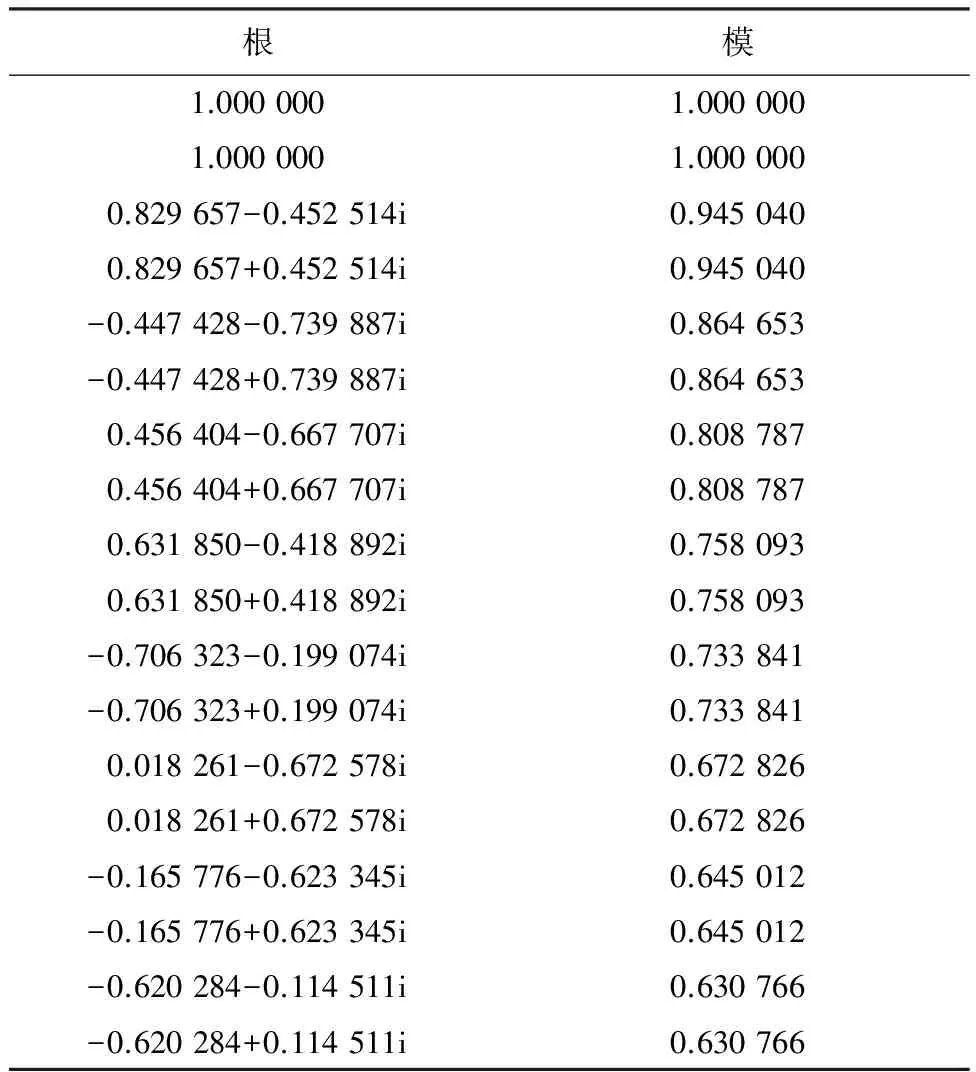
表11 VECM的平稳性检验

由表10、11检验结果可见，所构建的VAR以及VECM的根模的倒数在单位圆内．其中，如果VECM有r个协整关系，则会有k-r个根的模等于1．因此，所构建的VAR以及VECM都是稳定的，基于该模型的汽车销量预测结果是可靠的．

4.3 预测结果对比分析

为了对比分析本方法的性能，本文选取VAR和ARMA模型作为参照，选择平均绝对误差(mean absolute percentage error，MAPE)以及均方根误差(root mean square error，RMSE)来评判预测结果的准确性．对比结果如表12所示，可见采用VECM所得到的预测结果最优．

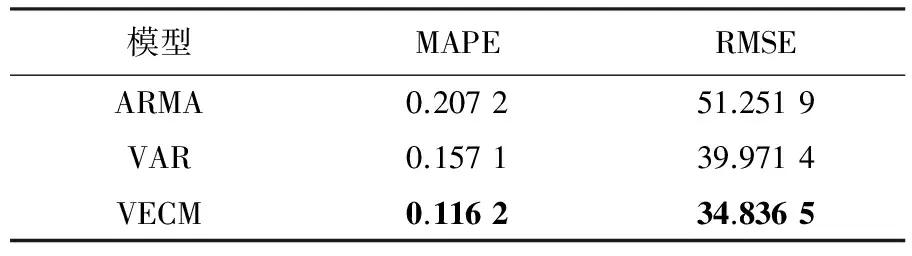
表12 预测结果比较

5 结 论

(1)中国汽车销量与宏观经济变量之间存在因果关系和长期均衡关系．单位根检验结果表明数据集里的原始变量不平稳且其一阶差分平稳．弱外生性检验以及格兰杰因果检验证明CCI和CPI是外生变量．协整检验表明汽车销量与汽油价格、钢材产量之间存在着长期均衡关系，且这种长期关系可以被VECM量化．

(2)与以往的年度汽车销量预测研究相比，本文以月为单位进行销量预测，更便于企业根据预测结果及时调整库存和优化供应链，更好应对汽车市场竞争．并且考虑了宏观经济变量对中国汽车销量的长期影响，通过平均绝对误差和均方根误差分析可发现：与VAR以及ARMA比较，本文提出的方法具有更高的预测精度．

[1] CHEN Yun, ZHAO Heng, YU Li. Demand forecasting in automotive aftermarket based on ARMA model [C] //2010InternationalConferenceonManagementandServiceScience,MASS2010. Piscataway: IEEE Computer Society, 2010:5577867.

[2] DU Hong, BO Cui. Sale forecasting method in dynamic environment based on ARMA(1,1) [C] //2011InternationalConferenceonElectricInformationandControlEngineering,ICEICE2011-Proceedings. Piscataway: IEEE Computer Society, 2011:4445-4448.

[3] 万莉敏. 我国燃料油期货市场有效性研究[D]. 哈尔滨:哈尔滨工程大学, 2010.

WAN Limin. The study on efficiency of Chinese fuel oil futures market [D]. Harbin:Harbin Engineering University, 2010. (in Chinese)

[4] 王云鹏,吴 迪,王占中,等. 基于协整分析的公路货运需求与国民经济的相关关系[J]. 吉林大学学报(工学版), 2011,41(1):56-61.

WANG Yunpeng, WU Di, WANG Zhanzhong,etal. Relationship between road freight transport demand and national economy development based on co-integration analysis [J].JournalofJilinUniversity(EngineeringandTechnologyEdition), 2011,41(1):56-61. (in Chinese)

[5] 李洪雄,汪浩瀚. 向量自回归模型与向量误差修正模型预测功能的比较——基于我国国内生产总值和居民消费支出变量的实证研究[J]. 宁波大学学报(理工版), 2011,24(2):119-123.

LI Hongxiong, WANG Haohan. Forecasting performance comparison between VAR and ECM:an empirical analysis on the variables of GDP and consumption in China [J].JournalofNingboUniversity(NaturalScience&EngineeringEdition), 2011,24(2):119-123. (in Chinese)

[6] SA-NGASOONGSONG A, BUKKAPATNAM S T S, KIM J,etal. Multi-step sales forecasting in automotive industry based on structural relationship identification [J].InternationalJournalofProductionEconomics, 2012,140:875-887.

[7] 黄飞雪,周 筠,李志洁,等. 基于协整和向量误差修正模型的中国主要城市房价的联动效应研究[J]. 中大管理研究, 2009,4(2):122-143.

HUANG Feixue, ZHOU Jun, LI Zhijie,etal. Relationships effect among housing prices of Chinese big cities based on cointegration and vector error correction model [J].ChinaManagementStudies, 2009,4(2):122-143. (in Chinese)

[8] DICKEY D A, FULLER W A. Likelihood ratio statistics for autoregressive time series with a unitroot [J].Econometrica, 1981,49(4):1057-1072.

[9] SAID S E, DICKEY D A. Testing for unit roots in autoregressive-moving average models of unknown order [J].Biometrika, 1984,71(3):599-607.

[10] ZHANG Yong, ZHONG Miner, GENG Nana,etal. Forecasting electric vehicles sales with univariate and multivariate time series models:The case of China [J].PLoSOne, 2017,12(5):e0176729.

[11] 俞立平,潘云涛,武夷山. 工业化与信息化互动关系的实证研究[J]. 中国软科学, 2009,1(1):34-40.

YU Liping, PAN Yuntao, WU Yishan. Study on relationship between industrialization and informatization [J].ChinaSoftScience, 2009,1(1):34-40. (in Chinese)

[12] GREENSLADE J V, HALL S G, HENRY S G B. On the identification of cointegrated systems in small samples:a modelling strategy with an application to UK wages and prices [J].JournalofEconomicDynamicsandControl, 2002,26(9/10):1517-1537.

[13] ENGLE R F, GRANGER C W J. Co-integration and error correction:representation, estimation, and testing [J].Econometrica, 1987,55(2):251-276.

[14] 邴其春,杨兆升,周熙阳,等. 基于向量误差修正模型的短时交通参数预测[J]. 吉林大学学报(工学版), 2015,45(4):1076-1081.

BING Qichun, YANG Zhaosheng, ZHOU Xiyang,etal. Short-term traffic parameters prediction method based on vector error correction model [J].JournalofJilinUniversity(EngineeringandTechnologyEdition), 2015,45(4):1076-1081. (in Chinese)

[15] FANTAZZINI D, TOKTAMYSOVA Z. Forecasting German car sales using Google data and multivariate models [J].InternationalJournalofProductionEconomics, 2015,170:97-135.