散货船配载仪中破舱稳性计算

沈 晔， 孙 霄 峰， 尹 勇， 刘 春 雷

( 大连海事大学 航海动态仿真和控制交通运输行业重点实验室， 辽宁 大连 116026 )

0 引 言

船舶在营运过程中一旦发生海损事故，舱室破损，极有可能造成船毁人亡的后果．为了减少这种风险，船舶在设计阶段就应考虑破舱稳性的问题．船舶破舱稳性是指船舶在舱室破损的情况下维持一定的浮态和稳性，防止或延缓沉没的一种能力，是船舶的重要性能．

传统的散货船破舱稳性计算基于船舶型值表或型线图，主要有郭洛瓦诺夫法、克雷洛夫-达尔尼法等[1]．姜玲[2]采用二次开发技术，在SolidWorks 的基础上，利用VB语言开发出一套破舱稳性计算程序；周瑞平等[3]使用B样条函数对船舶型值表中的数据进行处理，使用VB.NET和Access数据库开发出船舶稳性计算软件；段兴锋[4]利用Access数据库，以C++语言为开发工具，在MFC框架下开发出基于型值表的船舶装载仪；蔡晓梅[5]利用Maxsurf软件建立船体三维曲面模型，以此为数据来源进行破舱稳性计算；林焰等[6]用数据型值表描述船型，在水线面与船体表面求交时将坐标转换，运用格林公式计算水线面下船体和舱室的特征参数；肖维维等[7]对比了表面元法和基于NURBS曲面的最优化方法在破舱稳性计算中的差异，指出了两种方法存在的问题．

综上所述，国内大部分配载仪的数据来源都是型值表以及型线图或者在现有软件的基础上做二次开发．基于型值表或型线图的破舱稳性计算存在很大误差，尤其是运用于大角度倾斜下复杂船型破舱稳性的计算时误差更大，并且在船型数据输入模块，用户需要在型值表中读取或在型线图中量取大量描述船体的点坐标输入到软件中，十分费时费力．所以，将型值表或型线图作为数据来源的破舱稳性计算已经不能满足现代船舶设计的需要；而对现有的软件做二次开发也需要先建立模型，精度往往很差．

为了解决散货船配载仪中破舱稳性计算精度不高、操作复杂的问题，基于三维设计数据的破舱稳性计算法应运而生，国际上大部分知名配载仪软件，例如NAPA[8]、Maxsurf[9]等均基于船舶的三维设计数据进行计算，具有实时、高效、精确等优点，但其高昂的价格却是国内小型船舶公司承受不起的．而且由于商业保密的原因，这些软件的计算方法尚未可知．

本文基于船舶三维设计数据用最小功法和静平衡法进行散货船破舱稳性的计算，比较并分析两种方法的计算结果，并将精度较高的计算方法应用于散货船配载仪中破舱稳性计算模块．

1 船舶三维数据的获取

三维方法计算破舱稳性需要确定船体和破损舱室的型值数据，本文规定沿船艏方向为x轴的正方向，y轴左舷方向为正，z轴垂直于基平面向上为正．沿船长方向，按照装载手册中的肋位以一定的间隔垂直于x轴对船体进行切片，得到每个切片处的船舶横剖面型线数据，如图1所示．为得到船舶外板数据，需要对所得的型线数据进行等距偏移，偏移量为船壳的平均板厚，具体的实现方法见文献[10]．船舱型值数据的获取与此类似，但是不需要对其进行等距偏移．通过以上的方法可以得到船体外表面以及各舱室内表面的三维数据．

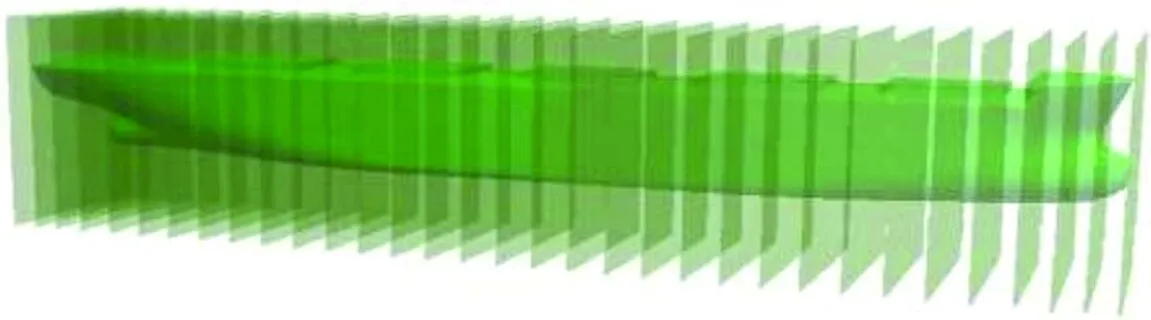
图1 散货船“RUI AN CHENG”型表面切片示意图

2 破舱稳性计算

目前散货船破舱稳性计算的方法主要有两种：一种是基于最小功原理的自由纵倾法，该方法固定船舶的横倾角，通过牛顿迭代法[11]或者优化法[12]求船舶达到特定横倾角时的纵倾和吃水，然后基于最小功原理可以求得船舶破舱后的稳性力臂，从而可以获得船舶的破舱稳性曲线；另一种是静平衡下的自由纵倾法，该方法分析船舶倾斜时的受力平衡状态，保证船舶横倾到指定角度时船舶所受外力和外力矩为零．

2.1 基于最小功原理的自由纵倾法

船舶在自由倾斜时会逐渐到达位能最小的位置．船舶在初始浮态的基础上横倾至指定角度，利用最小功原理建立优化模型，使用解析优化算法算出当前横倾角对应的稳性力臂．在相同载况下连续设定目标横倾角，求得对应的稳性力臂，绘制出破舱稳性曲线．相关的实现方法见文献[12]．

2.2 静平衡下的自由纵倾法

为了方便计算，引入下列符号：

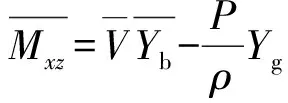
(1)

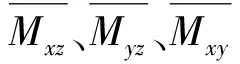
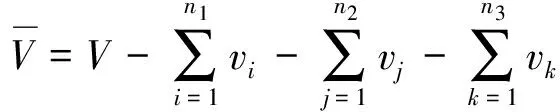
(2)

式中：n1、n2、n3分别为第1类、第2类、第3类破损舱室的总数；i、j、k分别为第1类、第2类、第3类破损舱室的编号，v、x、y、z分别为舱室进水体积和中心坐标；V、Xb、Yb、Zb为舱室破损后船体水下部分的体积和浮心坐标．以上数据可利用船舶吃水和横倾角通过对船舶三维数据进行积分求解．

由文献[13]可得破舱后的浮态平衡方程组：

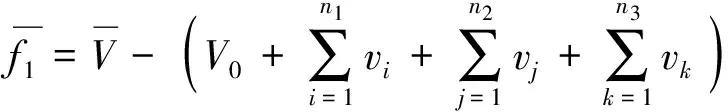
(3)

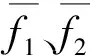
引入向量表示：

(4)

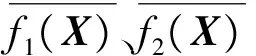
采用逐次线性化的方法得到方程组：

F′(Xk)ΔXk+F(Xk)=0；k=0，1，2，3，…

(5)

式中：Xk为经过k次迭代计算之后的结果；ΔXk为设定的计算精度，是迭代计算的停止条件；F′(Xk) 为F(X)在Xk处的Jacobi矩阵．根据船舶静力学原理，有

(6)

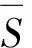
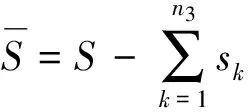
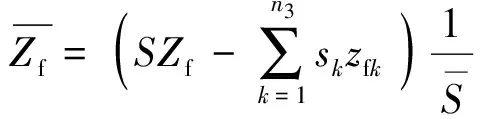
(7)

式中：S为破舱之后的水线面面积；s为进水舱室中的自由液面面积；Iyf为破舱之后的水线面对浮心的纵向惯性矩；iyf为进水舱室中自由液面对y轴的惯性矩．

2.3 程序设计

本文基于VS2013平台，使用C++语言编写破舱稳性的计算程序，具体的流程如图2所示．先将船体的三维设计数据进行等距偏移得到船壳外表面三维设计数据，基于船壳外表面三维设计数据和舱室三维设计数据，确定船舶倾斜后的横倾角，通过自由浮态计算简化方法[14]得到船舶破损后的浮态参数，利用这些浮态数据求得船舶破损稳性复原力臂．

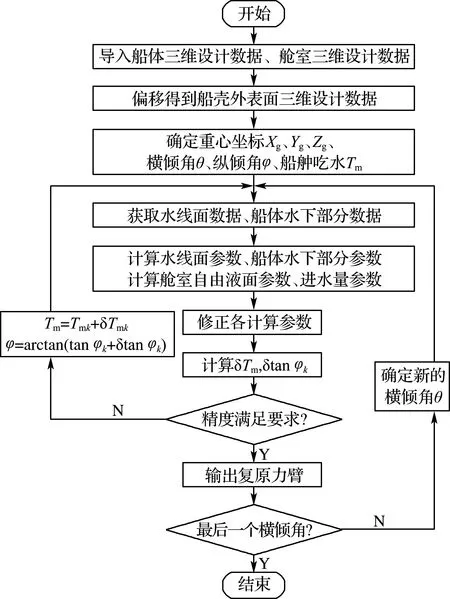
图2 破舱稳性计算流程图

3 算 例

本文基于散货船“RUI AN CHENG”的三维设计数据，分别求取了该船在3种不同载况下1号货舱破损、5号货舱破损以及1号货舱和5号货舱同时破损时船舶的复原力臂曲线，货舱的分布情况如图3所示，从船艏到船艉方向分别为1号货舱到5号货舱．

图3 散货船“RUI AN CHENG”货舱示意图

3种载况分别为轻质货满载出港、重质货均匀装载出港、重质货隔舱装载出港，如图4所示．

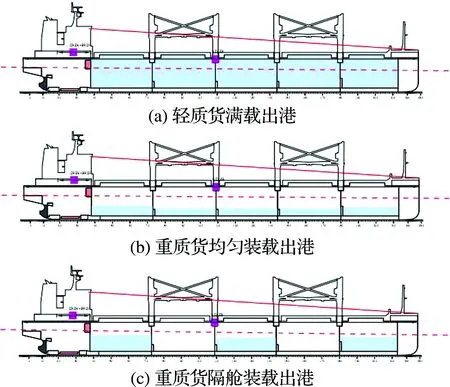
图4 3种典型载况

表1为3种载况对应的浮态参数．

本文以这3种典型载况下的浮态为初始条件进行迭代，计算出横倾角为0°～60°的复原力臂，然后将得到的复原力臂绘制成曲线与NAPA计算值进行比较．NAPA软件是由芬兰NAPA公司开发的国际著名的船舶CAD软件，目前大约有32个国家的320多家单位使用NAPA作为船

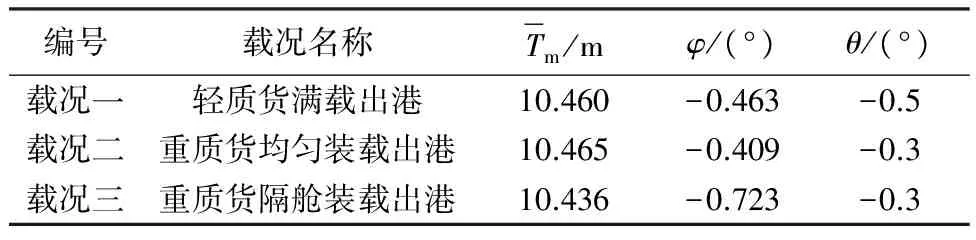
表1 典型载况

舶方案设计和技术设计的主要工具[15]．德国劳氏船级社和英国劳氏船级社等均将NAPA配载仪的计算结果作为标准值，根据与送检配载仪计算结果的比对判断送检配载仪是否达到认可标准．

3.1 载况一

在轻质货满载出港的载况下，利用最小功法和静平衡法分别在1号货舱破损、5号货舱破损以及1号货舱和5号货舱同时破损的情况下，求出横倾角为0°～60°时的复原力臂，并与NAPA计算值进行对比，如图5所示．

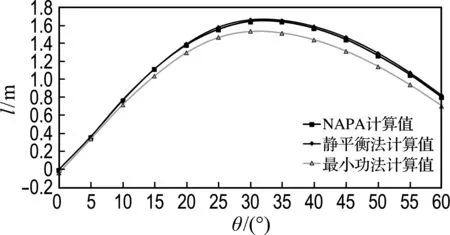
(a) 1号货舱破损

(b) 5号货舱破损

(c) 1号货舱和5号货舱同时破损

图5 载况一的复原力臂对比曲线

Fig.5 GZ curves comparison under the first loading condition

3.2 载况二

在重质货均匀装载出港的载况下，利用最小功法和静平衡法分别在1号货舱破损、5号货舱破损以及1号货舱和5号货舱同时破损的情况下，求出横倾角为0°～60°时的复原力臂，并与NAPA计算值进行对比，如图6所示．

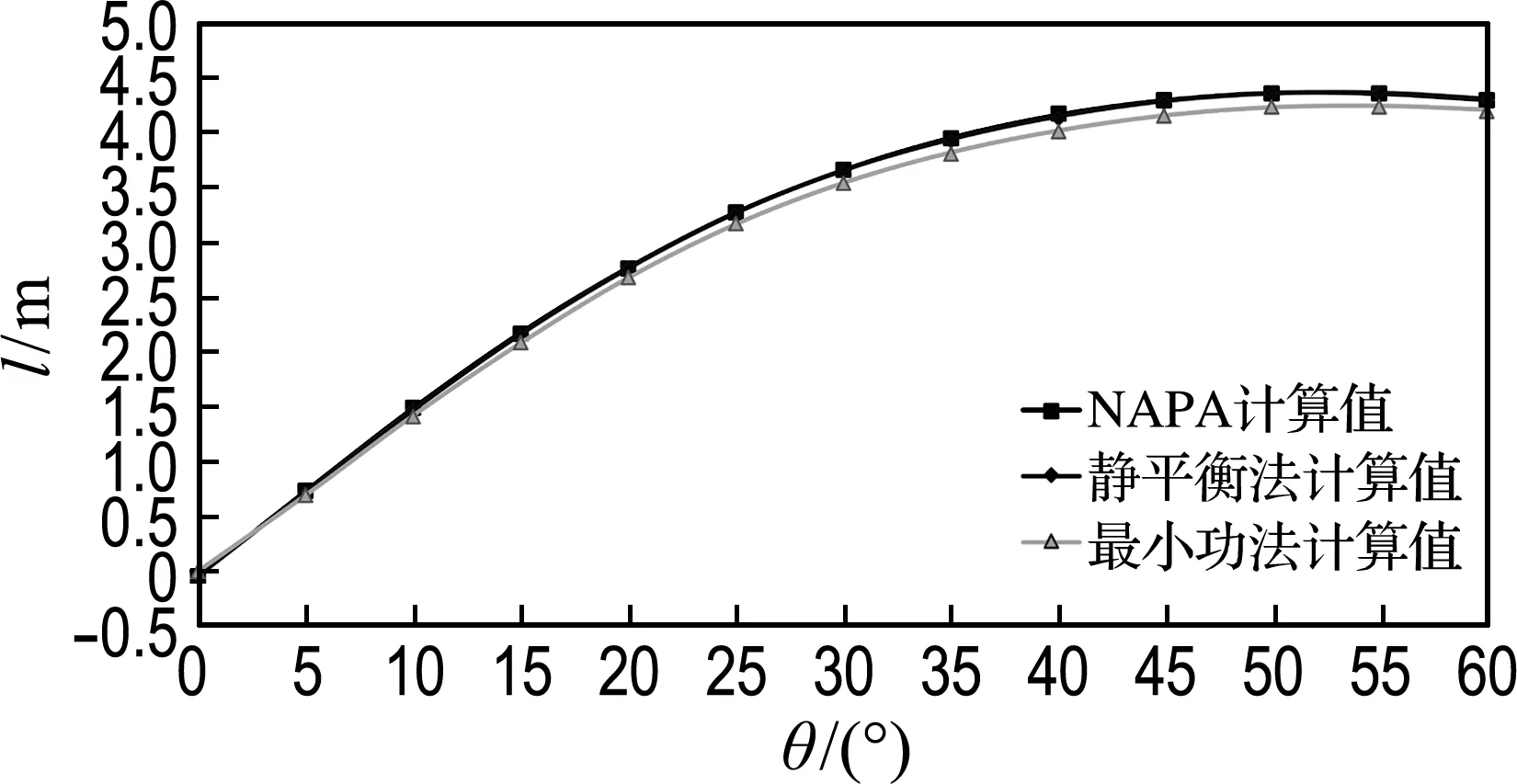
(a) 1号货舱破损

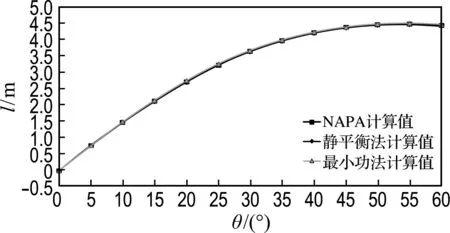
(b) 5号货舱破损

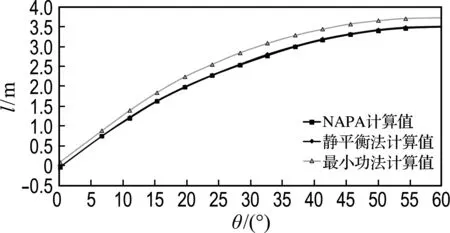
(c) 1号货舱和5号货舱同时破损

图6 载况二的复原力臂对比曲线

Fig.6 GZ curves comparison under the second loading condition

3.3 载况三

在重质货隔舱装载出港的载况下，利用最小功法和静平衡法分别在1号货舱破损、5号货舱破损以及1号货舱和5号货舱同时破损的情况下，求出横倾角为0°～60°时的复原力臂，并与NAPA计算值进行对比，如图7所示．

3.4 误差分析

将NAPA计算结果近似看作准确值，表2、3分别为使用最小功法和静平衡法计算产生的误差．

(a) 1号货舱破损

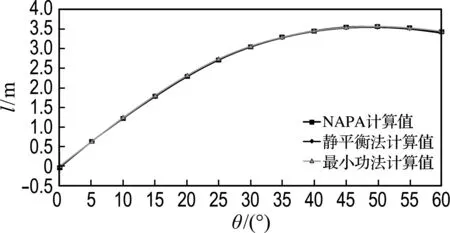
(b) 5号货舱破损

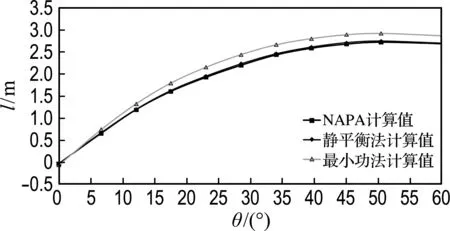
(c) 1号货舱和5号货舱同时破损

图7 载况三的复原力臂对比曲线

Fig.7 GZ curves comparison under the third loading condition

德国劳氏船级社[16]和英国劳氏船级社[17]对基于三维设计数据的散货船配载仪中的稳性计算误差要求最大不超过5 cm或5%．

利用最小功法进行破舱稳性的计算，117次计算中最大绝对误差为0.318 m(相对误差为10.82%)；每次计算的平均绝对误差为0.091 m(相对误差为1.86%)．实验证明本方法不符合船级社的精度要求，不适用于散货船配载仪中破舱稳性计算模块的实现．

利用静平衡法进行破舱稳性的计算，117次计算中最大绝对误差为0.031 m(相对误差为1.06%)；每次计算的平均绝对误差为0.013 m(相对误差为0.42%)，符合船级社的精度要求．而且在不同载况下，设置不同的横倾角，计算中迭代次数为3、4、5的概率为82.91%，迭代次数为6、7、8的情况只出现在横倾角超过50°时，满足计算的实时性要求，如图8所示．

最小功法不保证船舶横倾之后纵向外力和外力矩的平衡，所以计算结果和静平衡法有所差别．由误差分析可知，NAPA的破舱稳性计算模块使用的不是最小功法．

由实验结果可知，静平衡法计算船舶的破舱稳性与NAPA的计算结果较为接近．基于静平衡法，大连海事大学航海研究所成功完成了配载仪中的破舱稳性计算模块，并与上海船舶研究设计院联合开发了smart load型配载仪，该型配载仪的主界面如图9所示．目前，该配载仪已经通过CCS的认证并已顺利装船．

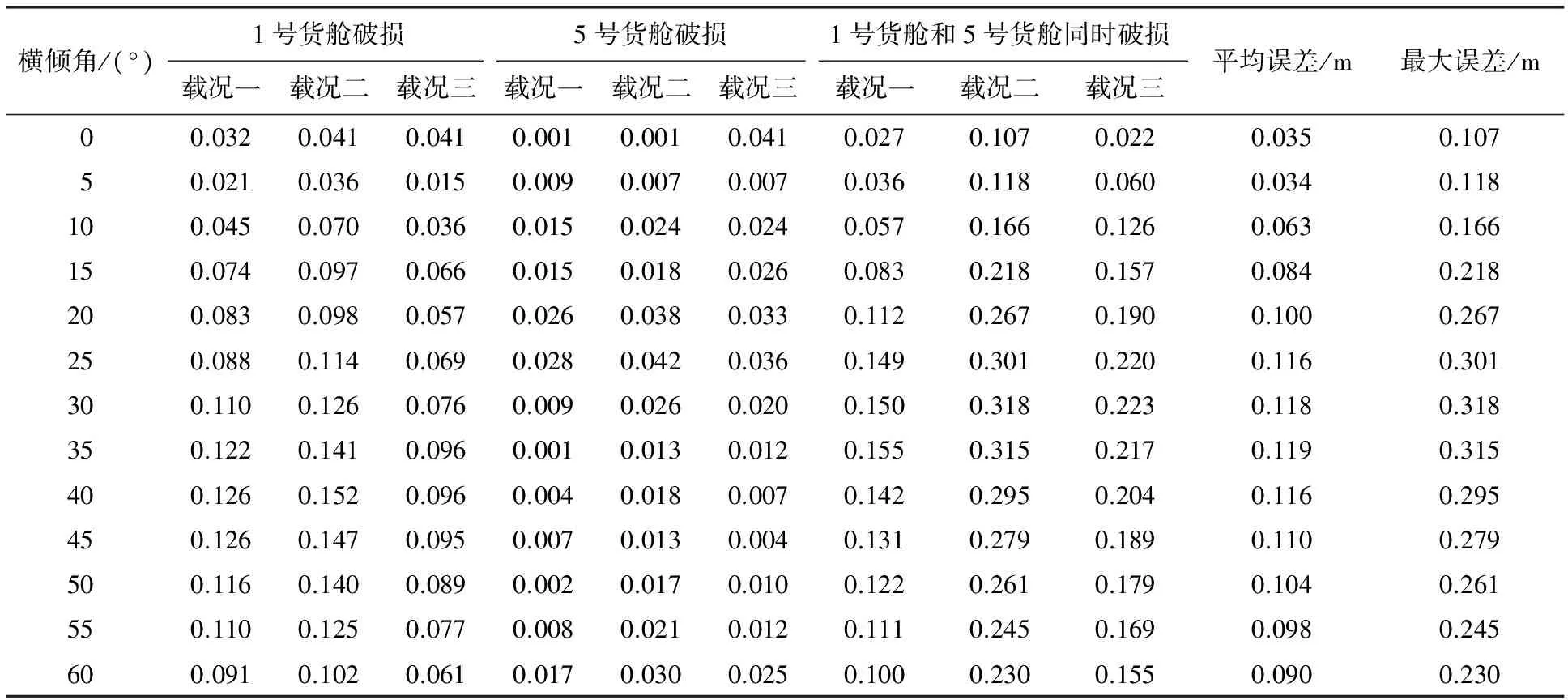
表2 最小功法计算结果绝对误差

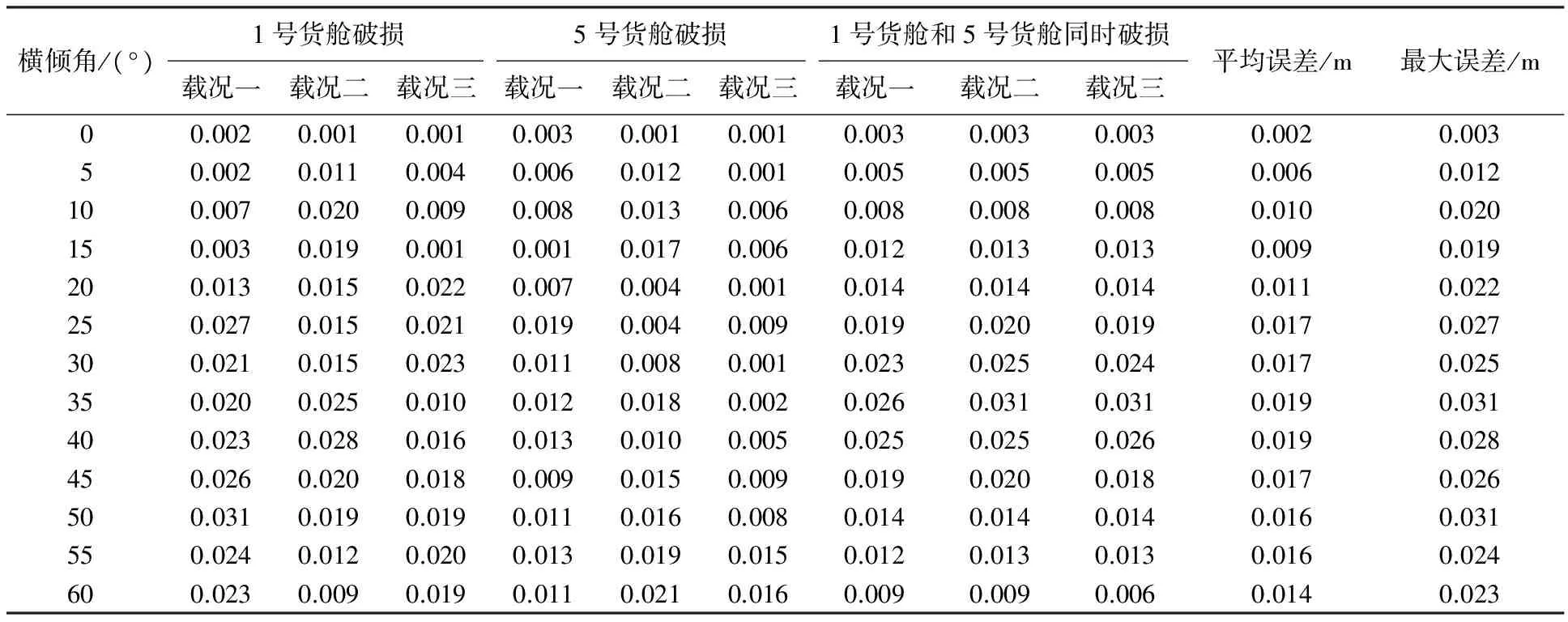
表3 静平衡法计算结果绝对误差

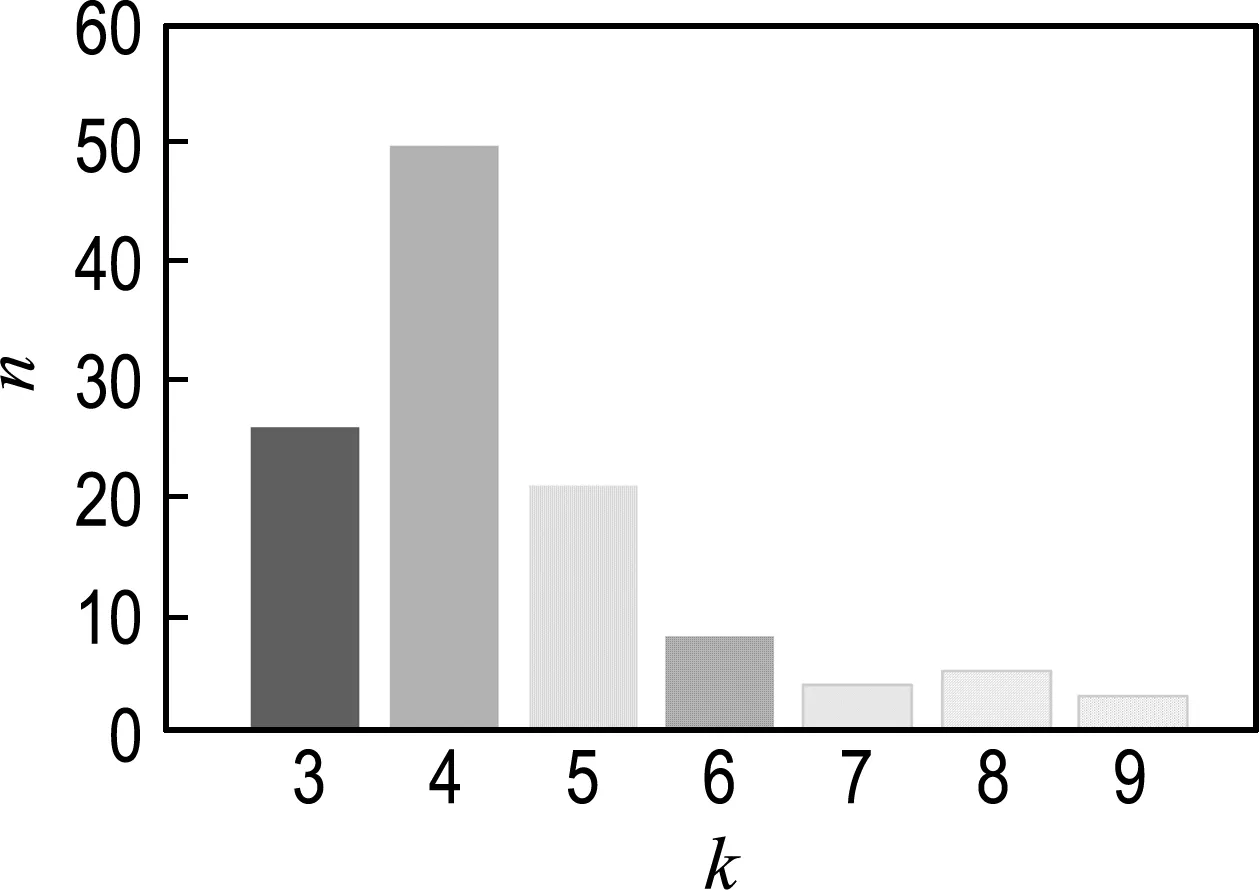
图8 破舱稳性计算迭代次数分布

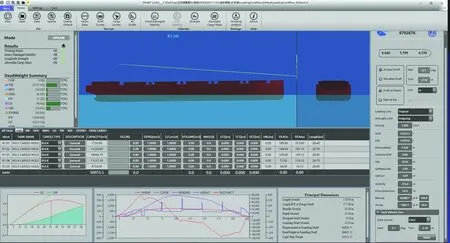
图9 散货船配载仪主界面

4 结 语

本文通过对船壳型表面数据进行船舶外板厚度的等距偏移，得到船体外板的设计数据，然后以适当的间隔沿船长方向进行切片得到船壳外表面的三维设计数据．以船舶外表面三维设计数据和舱室三维设计数据为基础进行破舱稳性的计算，得到破舱稳性曲线．通过对最小功法和静平衡法下的破舱稳性计算进行实现，发现运用不同的计算方法，得到的计算结果差异较大．使用静平衡下的自由纵倾法得到的计算结果与NAPA的计算结果较为接近．利用船舶的三维船壳模型计算破舱稳性具有较高的精度．本文介绍的方法不仅适用于散货船配载仪中破舱稳性计算模块的实现，对液货船、集装箱船等船型配载仪的开发也具有一定的参考价值．

[1] 盛振邦,杨尚荣,陈雪深. 船舶静力学[M]. 上海:上海交通大学出版社, 1984.

SHENG Zhenbang, YANG Shangrong, CHEN Xueshen.ShipStatics[M]. Shanghai:Shanghai Jiao Tong University Press, 1984. (in Chinese)

[2] 姜 玲. 船舶稳性三维计算方法研究及软件开发[D]. 大连:大连海事大学, 2015.

JIANG Ling. Ship stability dimensional calculation method research and software development [D]. Dalian: Dalian Maritime University, 2015. (in Chinese)

[3] 周瑞平,郭汝绯. 基于VB.NET的船舶稳性计算软件的设计和实现[J]. 造船技术, 2008,4(8):41-44.

ZHOU Ruiping, GUO Rufei. The design and realization of ship stability software based on VB.NET [J].MarineTechnology, 2008,4(8):41-44. (in Chinese)

[4] 段兴锋. 基于型值表的船舶装载仪的研究[D]. 大连:大连海事大学, 2008.

DUAN Xingfeng. Research of ship stowage system based on table of offsets [D]. Dalian: Dalian Maritime University, 2008. (in Chinese)

[5] 蔡晓梅. 应用三维船体曲面模型进行破舱稳性计算[J]. 江苏船舶, 2005,22(5):1-3.

CAI Xiaomei. Application of three-dimensional hull surface model in damaged stability calculation [J].JiangsuShip, 2005,22(5):1-3. (in Chinese)

[6] 林 焰,李铁骊,纪卓尚. 破损船舶自由浮态计算[J]. 大连理工大学学报, 2001,41(1):85-89.

LIN Yan, LI Tieli, JI Zhuoshang. Ship damage floating calculation [J].JournalofDalianUniversityofTechnology, 2001,41(1):85-89. (in Chinese)

[7] 肖维维,李俊华,何 刚,等. 船舶破舱稳性计算方法研究[J]. 中国水运, 2006,4(11):12-14.

XIAO Weiwei, LI Junhua, HE Gang,etal. Study of ship damage stability calculation [J].ChinaWaterTransport, 2006,4(11):12-14. (in Chinese)

[8] 王彩莲. 浅谈船舶应用软件NAPA[J]. 船舶, 2004(3):58-60.

WANG Cailian. On the ship design software NAPA [J].Ship&Boat, 2004(3):58-60. (in Chinese)

[9] 蒋毅文. Maxsurf及相关设计程序在船舶设计中的应用[J]. 船海工程, 2005(4):39-41.

JIANG Yiwen. Application of Maxsurf and corresponding software in ship design [J].Ship&OceanEngineering, 2005(4):39-41. (in Chinese)

[10] 刘春雷,尹 勇,孙霄峰,等. 基于STL模型的船舶几何特性计算[J]. 系统仿真学报, 2015,27(10):2264-2271.

LIU Chunlei, YIN Yong, SUN Xiaofeng,etal. Calculation of vessel′s geometric properties based on STL model [J].JournalofSystemSimulation, 2015,27(10):2264-2271. (in Chinese)

[11] 孙承猛,刘寅东. 一种船舶最小稳性和自由浮态计算的改进算法[J]. 中国造船, 2007,48(3):1-4.

SUN Chengmeng, LIU Yindong. An improved algorithm for calculating ship′s minimum stability and free floatation [J].ShipbuildingofChina, 2007,48(3):1-4. (in Chinese)

[12] 赵晓非,蔡伟科. 船舶稳性计算优化方法研究[J]. 中国造船, 1987,40(2):86-92.

ZHAO Xiaofei, CAI Weike. An optimization method for the calculation of ship stability curves [J].ShipbuildingofChina, 1987,40(2):86-92. (in Chinese)

[13] 赵晓非,林 焰. 关于解船舶浮态问题的矩阵方法[J]. 中国造船, 1985(3):55-64.

ZHAO Xiaofei, LIN Yan. Matrix methods for solving ship floating state problem [J].ShipbuildingofChina, 1985(3):55-64. (in Chinese)

[14] 刘春雷,尹 勇,孙霄峰,等. 散货船自由浮态计算简化方法[J]. 大连理工大学学报, 2017,57(1):55-60.

LIU Chunlei, YIN Yong, SUN Xiaofeng,etal. Simplified method of bulk carrier′s free floatation calculation [J].JournalofDalianUniversityofTechnology, 2017,57(1):55-60. (in Chinese)

[15] 刘春雷. 散货船智能化配载仪的研究与实现[D]. 大连:大连海事大学, 2013.

LIU Chunlei. Research and implementation of intelligent bulk carrier stowage system [D]. Dalian:Dalian Maritime University, 2013. (in Chinese)

[16] Germanischer Lloyd SE. Rules for Classification and Construction [Z]. Hamburg:Germanischer Lloyd SE, 2013.

[17] Lloyd′s Register. Approval of Longitudinal Strength and Stability Calculation Programs [Z]. London: Lloyd′s Register, 2011.