脉冲噪声环境下基于最大相关熵准则的仿射投影算法

刘 诚， 邱 天 爽*， 李 景 春， 李 蓉

( 1.大连理工大学 电子信息与电气工程学部, 辽宁 大连 116024；2.国家无线电监测中心， 北京 100037 )

0 引 言

以最小均方(LMS)算法、递归最小二乘(RLS)算法为代表的一类自适应滤波算法在信道均衡、系统辨识、噪声消除等领域有广泛的应用．LMS算法原理简单，计算量小，但是收敛速度较慢；RLS算法在收敛速度上比LMS算法快一个数量级，而它的代价是增加了计算复杂度[1]．

作为LMS算法的扩展又不同于LMS算法，仿射投影算法(APA)利用当前以及过去一段时间的输入值和观测值，即一个N阶的向量作为输入数据，取代LMS算法以单点作为输入数据的方法，可以有效地减少样本的梯度噪声，适用于输入数据频谱不平稳的情况．其算法性能介于LMS算法与RLS算法之间，在收敛速度和计算复杂度之间取得较好的平衡[2]．目前，针对仿射投影算法的研究主要集中在使用变步长的方法改善收敛性能上，文献[3]和文献[4]均利用仿射投影误差的范数修正步长的大小，没有从根本上改进算法的抗噪声能力．文献[5]用阶跃函数改进仿射投影算法的代价函数，由于阶跃函数只能取最大或最小值，在强脉冲噪声环境下算法的收敛速度下降．

传统的自适应滤波算法常以最小均方误差准则(MSE)作为代价函数，这样在假设噪声服从高斯分布或至少具有有限的二阶统计量的情况下，传统的算法会取得较好的收敛性能．而在自然环境或许多工程技术应用中，噪声常表现出一种脉冲状的非高斯性，并且往往具有很大的幅度，在数学上用稳定分布的模型来描述这一类噪声．目前常用的自适应滤波算法大多数的代价函数都是基于最小均方误差准则，包括仿射投影算法在内的这一类算法在稳定分布的噪声下会出现失调或者不收敛等情况[6]，无法满足自适应滤波的要求．针对稳定分布噪声的情况，Liu等在文献[7]中提出了最大相关熵准则(MCC)，基于这种准则开发的算法，可以在脉冲噪声条件下表现出较好的性能．在参数估计方面，文献[8]将MSE与MCC相结合修正仿射投影算法的目标函数，并在混合高斯噪声环境下取得较好收敛效果．文献[9]将最大相关熵准则与韧性子空间跟踪算法结合，证明了该算法在稳定分布噪声以及混合高斯噪声模型下具有更优的子空间跟踪性能．

在实际应用中，特别是在无线电监测环境下，接收信号常常会遇到脉冲性噪声的影响，使得无线定位或参数估计的结果与真实值有较大偏离．此外，若被监测的信号是运动的，则需要采用自适应算法对其进行动态估计．由此可见，无线电监测的实际问题亟须设计实现一种对于脉冲性噪声有较好抑制作用的自适应滤波或参数估计方法．综上，本文以最大相关熵准则为代价函数，改进仿射投影算法，推导出适用于脉冲噪声下的基于最大相关熵准则的仿射投影算法(MCCAPA)．并以SαS稳定分布(对称α稳定分布)为脉冲噪声模型，通过实验证明本文算法在适用于脉冲噪声环境的同时，具有较快的收敛速度和较好的收敛性能．

1 研究背景

1.1 SαS分布噪声模型

SαS分布噪声模型是唯一一类满足广义中心极限定理的分布．与高斯分布相比，SαS分布具有更厚的统计拖尾，因此在时域上具有显著的脉冲特性，可以很好地描述自然环境下或工程技术应用中具有较强脉冲性的噪声类型，其噪声模型的特征函数可以表示为

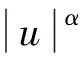
(1)

式中：0<α≤2，为特征指数，用于描述稳定分布过程的脉冲程度，且α取值越小，表现出越强的脉冲性，当α=2时，稳定分布退化为高斯分布；a∈R，为位置参数，表示分布的均值或中值；γ∈(0，∞)，为分散系数，用于描述分布的分散情况[10-11]．通过上述模型可以很好地构造出在实际中普遍存在的具有较强脉冲性的非高斯现象．因此，本文选择SαS分布来构造脉冲噪声环境．

1.2 最大相关熵准则

对于两个随机变量X和Y，其相关熵的定义为

Vσ(X，Y)=E[κσ(X-Y)]

(2)

其中E[·]为期望，κσ(·)为核函数，σ为核长．

核函数可以减少把输入数据从低维空间到高维空间映射后产生的计算量，同时映射到高维空间的维数越大，区分输入数据差异的性能越好．其中，高斯核函数可以将输入数据映射到无限维空间，而其余的方法只能映射到有限维空间，故选择高斯核函数代入相关熵的表达式可得到：

(3)

文献[7]提出了相关熵可以诱导出一个测度距离(correntropy induced metric，CIM)，并给出CIM的表达式为CIM(X，Y)=[κσ(0)-Vσ(X，Y)]1/2．实际上，最大相关熵准则是依据最大化相关熵Vσ(X，Y)等价于最小化CIM(X，Y)这一性质的，即当测度距离越小时，两个变量的相似程度越高，其相关熵的值越大．因此，依据最大相关熵准则，当Vσ(X，Y)取得最大值时，两个随机变量X和Y的误差e(i)=X(i)-Y(i)最小[12]．

2 算法介绍

2.1 仿射投影算法

设u为n×1维的零均值随机变量，d为一个零均值随机标量，w为自适应滤波器的系数向量，给出基于最小均方误差准则的代价函数为

minJ(w)=E[(d-wTu)2]

(4)

由式(4)可知，仿射投影算法滤波器权值的最佳解表达式为

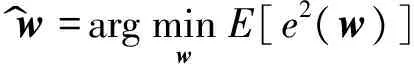
w＾=argminwE[e2(w)]

(5)

w(i)=w(i-1)+η(Ru+εI)-1[rdu-Ruw(i-1)]

(6)

其中ε为平滑因子，是一个小的正数；η为人工设定的步长．在实际的滤波过程中，理论上无法获得完整的协方差矩阵，仿射投影算法采用当前与之前共K个时刻的输入值和观测值来估计Ru和rdu的值，即

R＾u=1KU(i)UT(i)

r＾du=1KU(i)d(i)

(7)

其中U(i)=(u(i-K+1) …u(i))n×K，d(i)=(d(i-K+1) …d(i))T．将估计值代入式(6)，得到仿射投影算法的递推公式为

w(i)=w(i-1)+ηU(i)[UT(i)U(i)+εI]-1·

[d(i)-UT(i)w(i-1)]

(8)

2.2 基于最大相关熵准则的仿射投影算法

仿射投影算法在高斯噪声环境下可以取得较好的收敛性能，但是在脉冲噪声环境下，由于它的代价函数是基于最小均方误差准则的，不存在有限的二阶或高阶统计量，会使算法性能退化，或者出现不收敛的情况．为此，本文提出基于最大相关熵准则的仿射投影算法(MCCAPA)，使得其在脉冲噪声环境下取得较好的效果．

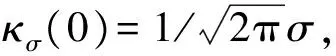
minE[ρ(e(i))]=minE[κσ(0)-κσ(e(i))]=

minE[(1-exp(-e2(i)/

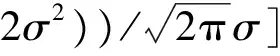
maxE[exp(-e2(i)/2σ2)/

maxE[κσ(e(i))]

(9)

式中“⟺”表示等价转换，根据上式的转换得到基于最大相关熵准则的代价函数为

maxJ(w)=maxE[κσ(e(i))]=

wnTu(i))2/2σ2)]

(10)

由代价函数可以得到基于最大相关熵准则的仿射投影算法滤波器最佳权值表达式为

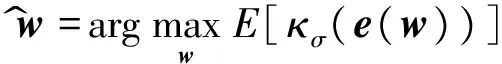
w＾=argmaxwE[κσ(e(w))]

(11)

应用平滑牛顿递归算法推导出递归方程：

w(i)=w(i-1)+η(Ru+εI)-1J(w)=

(12)

其中e(i)为n×K阶矩阵．

根据M估计自适应滤波理论，可以得到最大相关熵准则代价函数的维纳解为

(13)

式中：Rκ，u为输入矩阵U(i)的自协方差矩阵，rκ，du为输入矩阵U(i)与目标矩阵d(i)的互协方差矩阵，应用仿射投影算法原理得到估计式为

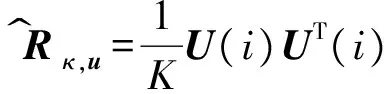
R＾κ，u=1KU(i)UT(i)

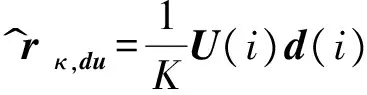
r＾κ，du=1KU(i)d(i)

(14)

将上式代入式(12)，利用矩阵求逆引理，得到MCCAPA的递推公式为

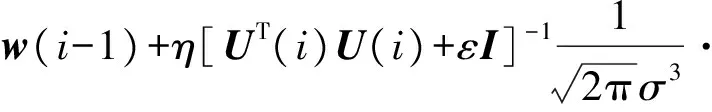
(15)

其中e(i)=d(i)-UT(i)w(i-1)．

给出MCCAPA实现步骤如下：

(1)初始化w(0)=0，选择步长η，核长σ．

(2)计算

y(i)=UT(i)w(i-1)

e(i)=d(i)-y(i)

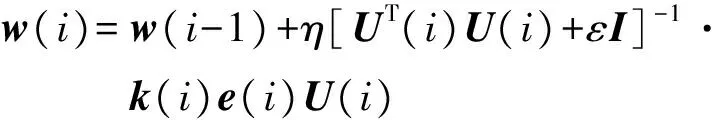
(3)重复(2)至均方误差值收敛于稳态误差．

MCCAPA利用最大相关熵准则作为代价函数，先由迭代误差代入最大相关熵准则的代价函数计算出一个权值k(i)，再代入迭代公式进行迭代．当迭代误差e(i)受到脉冲噪声的影响而增大时，权值k(i)减小，将权值代入迭代公式得到滤波器系数w(i)的变化较小，从而保证了算法不会受到脉冲噪声的影响而出现不收敛或收敛性能下降的情况；反之，当迭代误差e(i)较小时，权值k(i) 较大，保证了算法可以取得较快的收敛速率．

MCCAPA通过误差自适应地控制迭代公式中滤波器系数的大小，既可以在迭代过程中使得滤波器系数免受脉冲噪声的影响，保证算法的收敛性能，也可以在噪声较小时快速调整滤波器的系数，保证算法的收敛速度．

3 仿真实验

本文采用维纳模型构建的非线性信道均衡问题来考查各算法性能，其模型结构如图1所示．

在维纳模型中，输入信号先经过线性变换，再经过非线性变换，施加噪声，得到接收机接收信号r(n)[13]．本文仿真信号采用BPSK信号，线性变换公式为

x′(n)=x(n)+0.5x(n-1)

(16)

图1 维纳非线性信道模型

非线性变换公式为

y(n)=x′(n)-0.5[x′(n)]2-0.2[x′(n)]3

(17)

将BPSK信号通过式(16)、(17)处理后，再施加稳定分布噪声，最终得到接收信号r(n)．

SαS分布在α<2时二阶矩无界，因此引入广义信噪比(generalized SNR，Rgsn)的概念．本文将在不同α取值以及不同广义信噪比的情况下讨论MCCAPA与APA的收敛速度和误差性能的差别，并将讨论在不同核长选择的情况下，MCCAPA的误差性能．

实验1在MCCAPA的核长取值、步进取值均为最佳的条件下，设定广义信噪比为10 dB，在广义信噪比较理想的情况下比较噪声的冲激程度对各算法的影响．α=1.8时，噪声冲激程度较小，接近于高斯噪声，进行100次蒙特卡罗实验，得到两种算法的学习曲线如图2所示．可以观察到，MCCAPA取得较快的收敛速度，APA收敛速度较慢．学习曲线稳定后MCCAPA的误差控制性能要稍好于APA．

图2 α=1.8时学习曲线

逐步减小α的取值，使噪声的冲激程度不断加大．当α=1.1时，如图3所示，在受到严重冲激噪声干扰的情况下，MCCAPA收敛速度较快，且出现波动后可以快速收敛．而APA会出现学习曲线突变后不收敛的情况，不适用于强冲激噪声的恶劣情况．

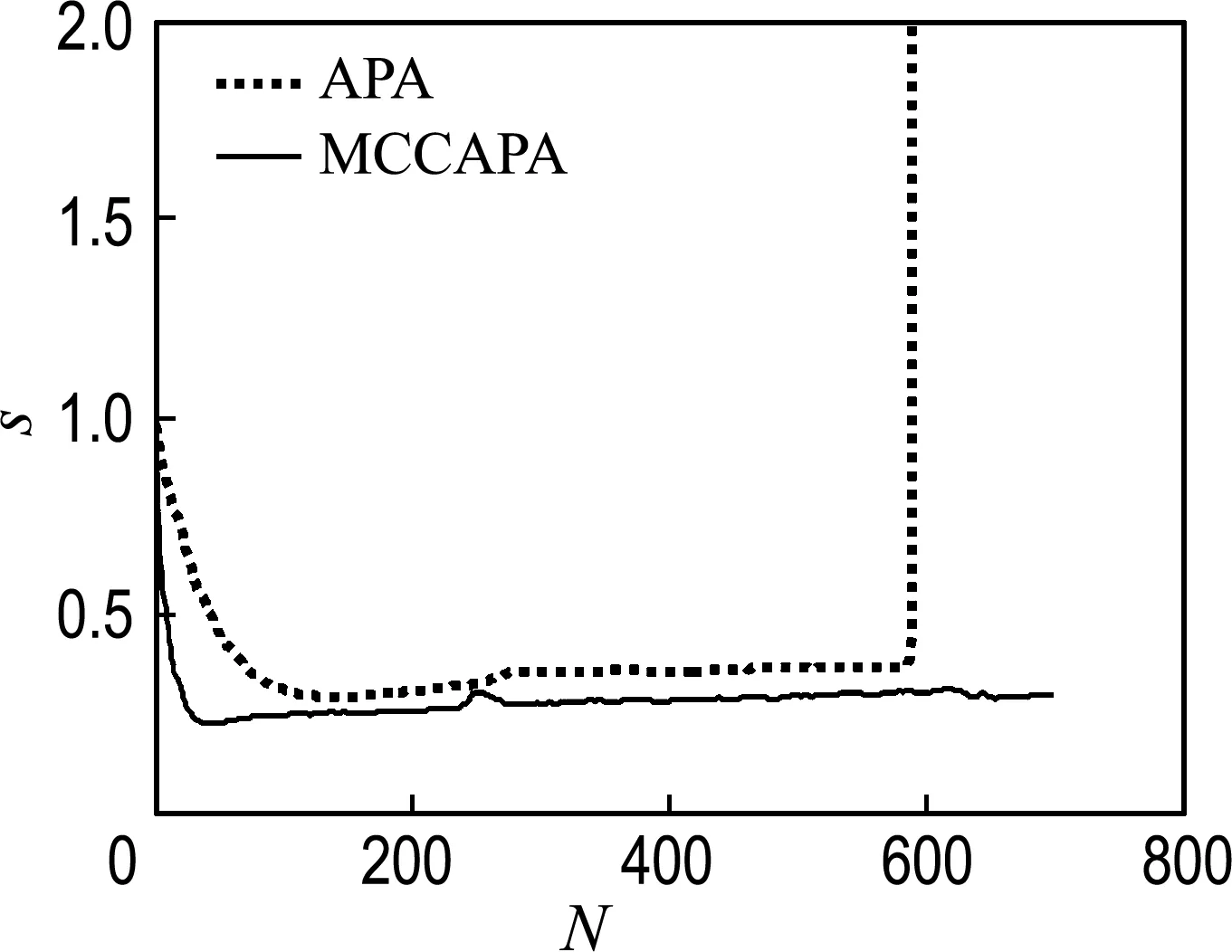
图3 α=1.1时学习曲线

继续减小α的值，MCCAPA受冲激噪声的影响不大，且具有较好的韧性，而APA则出现不收敛的情况，算法不适用．图4给出了在广义信噪比为10 dB时均方误差随α变化的情况，可以观察到，MCCAPA在脉冲噪声环境下的稳态误差要小于APA，且在强脉冲噪声环境下，APA不收敛，无法使用．

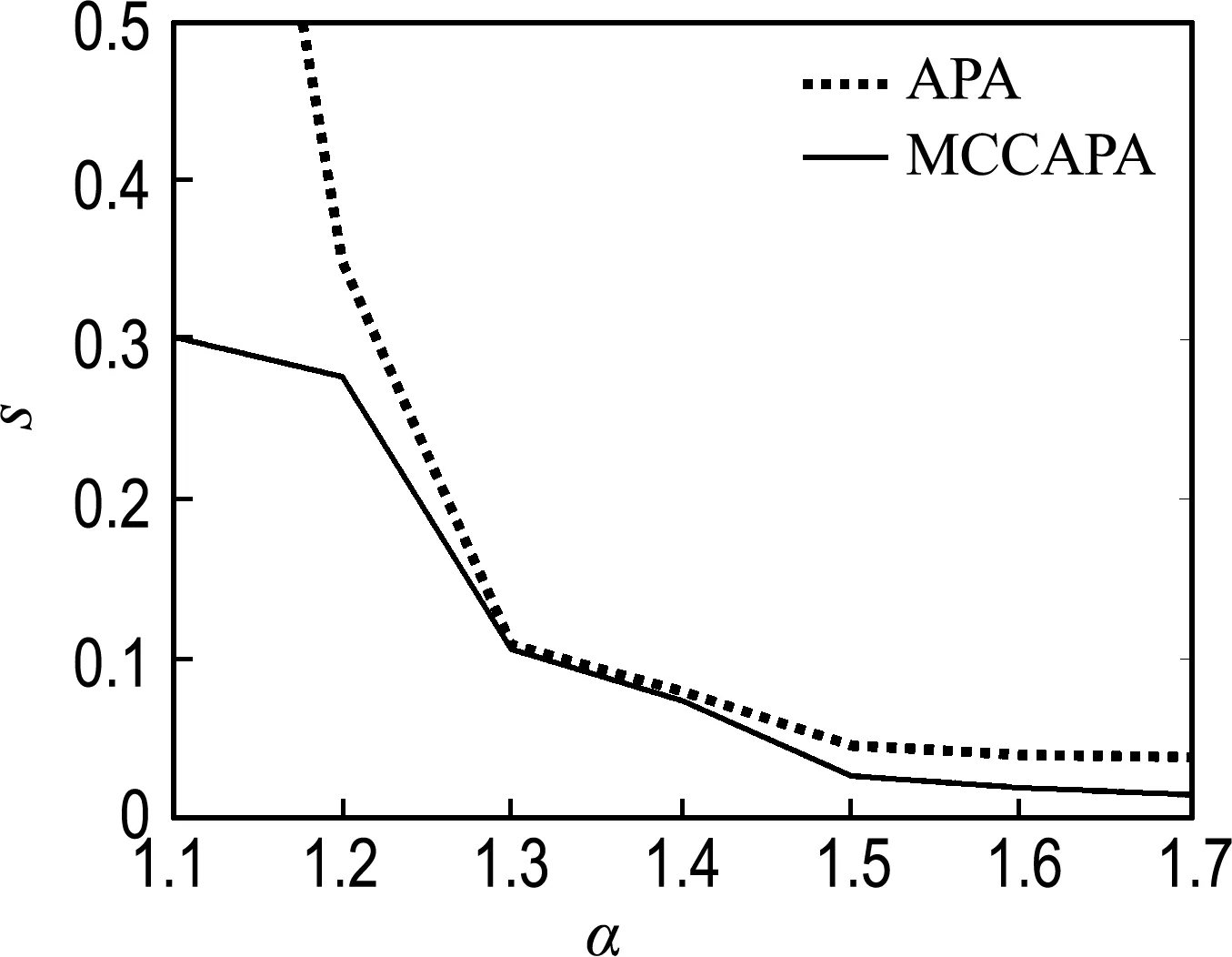
图4 GSNR为10 dB时均方误差随α变化情况

实验2设α=1.6保持不变，改变广义信噪比的值，观察两种算法在不同广义信噪比下的性能．在广义信噪比较高的情况下，两种算法的收敛情况与图2相似．逐步减小广义信噪比的值，当广义信噪比为4 dB时，如图5所示，APA会发生不收敛的情况，MCCAPA收敛性能较好，并且MCCAPA 收敛速度更快，稳态波动较小．

图5 GSNR为4 dB时学习曲线

图6给出在α=1.6保持不变的情况下改变广义信噪比，两种算法在迭代第600次时均方误差随广义信噪比的变化情况．

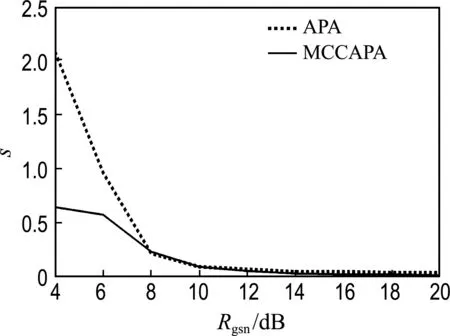
图6 α=1.6时均方误差随广义信噪比变化情况

当广义信噪比的值小于8 dB时，APA会出现稳定误差变大的情况，算法的收敛性能较差．如图6所示，在广义信噪比较大，即实验环境较理想的情况下，两种算法的稳态误差相差不大，MCCAPA 的误差较小，体现了自适应滤波的效果较好．随着广义信噪比的减小，两种算法的稳定误差都会随之增大，然而在较为恶劣的情况下，APA的误差会显著增加，可以看出MCCAPA在收敛性能以及误差控制上优于APA．

实验3在理想条件下，针对MCCAPA，讨论核长σ对收敛性能的影响．核长是高斯核中用来抑制噪声干扰的重要参数，鉴于目标信号和噪声的多样性、复杂性，无法通过理论推导的方式确定核长的最优解，而是通过大量仿真实验来确定最合适的核长．表1给出广义信噪比为20 dB、α=1.8 的情况下，核长在0～2.0变化，MCCAPA在迭代第600次时均方误差．

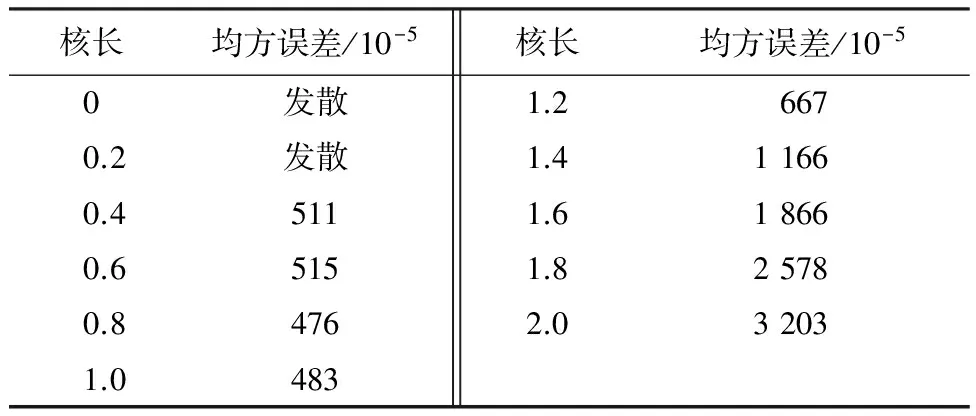
表1 均方误差随核长的变化情况

观察可知，当核长在0～2.0变化时，均方误差总体上呈现出先下降再上升的趋势，在σ=0.8时取得最小值．

4 结 语

针对最小均方误差准则在脉冲噪声情况下性能不好的问题，本文使用最大相关熵准则修正仿射投影算法的代价函数，推导出基于最大相关熵准则的仿射投影算法．并通过实验证明在冲激性较强以及信噪比较低等情况下，新算法MCCAPA 都具有比较好的收敛速度与较小的稳态误差，更加适应于实际应用中的情况．

[1] SAYED A H.AdaptiveFilters[M]. New York: Wiley-IEEE Press, 2008.

[2] GONZALEZ A, FERRER M, ALBU F,etal. Affine projection algorithms:Evolution to smart and fast algorithms and applications [J].EuropeanSignalProcessingConference, 2012:6333930.

[3] SHIN H C, SAYED A H, SONG W J. Variable step-size NLMS and affine projection algorithms [J].IEEESignalProcessingLetters, 2004,11(2):132-135.

[4] XIAO Longshuai, WU Ming, YANG Jun. A new efficient filtered-x affine projection sign algorithm for active control of impulsive noise [J].SignalProcessing, 2016,120:456-461.

[5] ZHENG Zongsheng, ZHAO Haiquan. Memory improved proportionate M-estimate affine projection algorithm [J].ElectronicsLetters, 2015,51(6):525-526.

[6] WANG Bing, CUI Guolong, YI Wei,etal. Approximation to independent lognormal sum withα-μdistribution and the application [J].SignalProcessing, 2015,111:165-169.

[7] LIU Weifeng, POKHAREL P P, PRINCIPE J C. Correntropy: properties and applications in non-Gaussian signal processing [J].IEEETransactionsonSignalProcessing, 2007,55(11):5286-5298.

[8] YANG Xiaohan, QU Hua, ZHAO Jihong,etal. Hybrid affine projection algorithm [C] //201413thInternationalConferenceonControlAutomationRoboticsandVision,ICARCV2014. Piscataway: IEEE, 2015:964-968.

[9] 张金凤,邱天爽,李 森. 冲激噪声环境下基于最大相关熵准则的韧性子空间跟踪新算法[J]. 电子学报, 2015,43(3):483-488.

ZHANG Jinfeng, QIU Tianshuang, LI Sen. A robust PAST algorithm based on maximum correntropy criterion for impulsive noise environments [J].ActaElectronicaSinica, 2015,43(3):483-488. (in Chinese)

[10] 邱天爽,张金凤,宋爱民,等. 脉冲噪声下基于广义类相关熵的DOA估计新方法[J]. 信号处理, 2012,28(4):463-466.

QIU Tianshuang, ZHANG Jinfeng, SONG Aimin,etal. The generalized correntropy-analogous statistics based direction of arrival estimation in impulsive noise environments [J].SignalProcessing, 2012,28(4):463-466. (in Chinese)

[11] TSIHRINTZIS G A, NIKIAS C L. Fast estimation of the parameters of alpha-stable impulsive interference [J].IEEETransactionsonSignalProcessing, 1996,44(6):1492-1503.

[12] SINGH A, PRINCIPE J C. Using correntropy as a cost function in linear adaptive filters [C] //2009InternationalJointConferenceonNeuralNetworks,IJCNN2009. Piscataway: IEEE, 2009:2950-2955.

[13] ABD-ELRADY E. A nonlinear approach to harmonic signal modeling [J].SignalProcessing, 2004,84(1):163-195.