对一道抛物线联赛题的探究与拓展*

北京市第十二中学高中部(100071) 刘刚 赵毅

题目(2017年全国高中数学联赛一试(B卷)11题)在平面直角坐标系xOy中,曲线C1∶y2=4x,曲线C2∶(x−4)2+y2=8.经过C1上一点P作一条倾斜角为45°的直线l,与C2交于两个不同的点Q,R,求|PQ|·|PR|的取值范围.

试题以抛物线、圆为背景,考查了抛物线、圆的标准方程、直线与圆的位置关系、距离乘积的范围以及转化、数形结合等数学思想,检验了运算与求解、分析问题与解决问题的能力.试题平中见奇,解法多样,符合新课标理念,是一道不折不扣的好题.

1.解法探究

解法1 设Q(x1,y1),R(x2,y2),P(m2,2m),由直线l的倾斜角为45°,得直线l的方程为y−2m=x−m2,即y=x+2m−m2.代入曲线C2的方程(x−4)2+y2=8,即(x−4)2+(x+2m−m2)2=8,整理,得2x2−2(m2−2m+4)x+(m2−2m)2+8=0,所以

因为直线l与C2有两个不同的交点,所以

由直线l的倾斜角为45°,得

由②,得0＜m2＜4_或4＜m2＜16,所以(m2−2)2∈[0,4)∪(4,196),故(m2−2)2+4∈[4,8)∪(8,200),即|PQ|·|PR|的取值范围是[4,8)∪(8,200).

解法2 设P(m2,2m),由直线l的倾斜角为45°,得l的方程为y−2m=x−m2,即

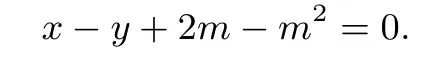
因为曲线C2∶(x−4)2+y2=8,所以C2是以(4,0)为圆心,半径的圆.因为l与C2有两个不同的交点,所以

设C2的圆心为M,由圆幂定理,得|PQ|·|PR|=|PM|2−r2=(m2−4)2+(2m)2−8=(m2−2)2+4.以下同解法1.

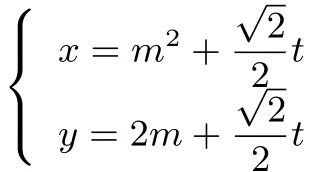
该方程有两个实数根,设为t1,t2,则t1t2=m4−4m2+8.由t的几何意义,得

以上用了3种方法对试题进行求解.解法1先根据直线l与曲线C2有两个不同的交点,借助判别式求出参数m的范围,然后利用弦长公式表示出|PQ|·|PR|再进一步求解;解法2先挖掘图形特征,把直线l与曲线C2有两个不同的交点问题转化为圆心到直线的距离小于半径,从而求出参数m的范围,然后借助圆幂定理及勾股定理表示出|PQ|·|PR|再进一步求解;解法3利用直线的参数方程进行求解.解法1是通解通法,但运算量较大;解法2充分利用圆的几何性质,大大减少运算量,但有一定的局限性;解法3根据所求代数式特点“一条直线上同一点出发的两条线段之积”联想直线的参数方程,使解题更有针对性,并且这种方法具有普适性特点.利用直线的参数方程解决有关线段长度问题时,往往能起到事半功倍的效果,下面举例说明,供大家参考.

2.拓展

例1(2017年内蒙古自治区高中数学联赛预赛)过抛物线y2=2px(p＞0)的焦点F作弦BC,若BC的中垂线交BC于M,交x轴于N,求证:|MN|2=|FC|·|FB|.

例2(2016年浙江高中数学竞赛)已知椭圆C∶,经过点,离心率为.过椭圆C的右焦点作斜率为k的直线l,交椭圆于A,B两点,记PA,PB的斜率为k1,k2.

(1)求椭圆的标准方程;

(2)若k1+k2=0,求实数k的值.

例3(2016年高考四川理科第20题)已知椭圆E∶的两个焦点与短轴的一个端点是直角三角形的3个顶点,直线l∶y=−x+3与椭圆E有且只有一个公共点T.

(1)求椭圆E的方程及点T的坐标;

(2)设O是坐标原点,直线l′平行于OT,与椭圆E交于不同的两点A,B,且与直线l交于点P.证明:存在常数λ,使得,并求λ的值.

解(1)椭圆E的方程为,点T的坐标为(2,1)(过程从略).

(2)因为点P在直线l∶y=−x+3上,所以设P(x0,3−x0).因为T(2,1),所以,所以直线l′的参数方程为

例4(2016年湖南高中数学竞赛)如图1,已知椭圆经过点,离心率为,直线l经过椭圆C的右焦点F交椭圆于A,B两点,点A,F,B在直线x=4的射影依次为D,K,E.

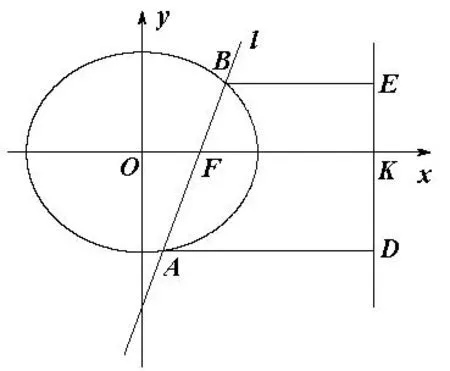
图1

(1)求椭圆C的方程;

(2)连接AE,BD,试探求当直线l的倾斜角变化时,直线AE与BD是否相交于定点?若是,请求出定点的坐标并给予证明;否则,说明理由.

所以|FN|·|AB|=|FA|·|BE|,即点在直线AE上.同理,可得点也在直线BD上.所以,当直线l的倾斜角变化时,直线AE与BD相交于定点.

在解决解析几何问题时,一定要认真分析题目特点,不盲目套用某种方法,要具体问题具体分析,及时调整解题策略,这样才能避免题海战,真正提高复习效率.