矩阵随机赋范空间上函数方程的Ulam稳定性

宋爱民，李跃武

甘肃民族师范学院数学系, 甘肃合作 747000

矩阵赋范空间经常被用来刻画有界的希尔伯特空间算子组成的线性空间的抽象性质，同时，在C*-代数中， 矩阵赋范空间上的一些性质，可以用来进一步研究Haagerup张量积和商空间的相关性质[1]．实际上，在矩阵赋范空间上，商空间与不同算子空间的Haagerup张量积组成了一个新的算子空间，正是基于这一理论，算子空间理论成为算子代数理论研究中的重要分支[2]．

1940年ULAM[3]就提出函数方程的稳定性问题，研究了群同态的稳定性．HYERS[4]针对Banach空间中近似可加映射的稳定性首次给出了肯定的回答．RASSIAS[5]进一步将这种稳定性推广到广义Hyers-Ulam-Rassias稳定性．近年来，人们研究了各种映射的Ulam稳定性[6-8]．RADU[9]利用不动点方法讨论了可加函数方程的稳定性问题，显示出不动点方法在证明函数方程稳定性中的重要作用，不动点方法成为研究函数方程稳定性的重要方法．LEE等[10]研究了矩阵赋范空间中可加函数方程和2次函数方程的Ulam稳定性，之后，数学家研究了各种矩阵赋范空间上函数方程的稳定性问题[11-13]．

GORDJI等[14]给出以下混合3次-4次函数方程：

4[f(3x+y)+f(3x-y)]=12[f(2x+y)+

f(2x-y)]-12[f(x+y)+f(x-y)]+

f(2y)-8f(y)+30f(2y)-192f(x)

(1)

并在Banach空间讨论其Ulam稳定性．

本研究在文献[10-13]基础上，给出矩阵随机赋范空间的定义，并在其上讨论函数方程(1)的Ulam稳定性．

1 预备知识

设Γ+={F:∪{-∞,+∞}→[0,1]，F左连续，在上不减，F(0)=0,F(+∞)=1}， 显然集合D+={F∈Γ+:l-(+∞)=1}. 其中，为Γ+的子集合，Γ+是一个偏序集满足∀F,G∈Γ+,F≤G⟺F(t)≤G(t)， 对所有t∈成立．对任意a≥0,Ha(t)∈D+定义为

显然，H0(t)为Γ+中的最大元．

定义1[15]函数T:[0,1]×[0,1]→[0,1]称为三角范数(简称t范数)，若满足

1)T满足交换律和结合律，即T(a,b)=T(b,a)；T(a,T(b,c))=T(T(a,b),c)；

2)T(a,1)=a， 对任意a∈[0,1]成立；

3) 若∀a,b,c,d∈[0,1]， 满足a≤c,b≤d， 则T(a,b)≤T(c,d)；

显然Tp(a,b)=ab;TL(a,b)=max{a+b-1,0};TM(a,b)=min{a,b}皆为连续的t范数．

定义2[16]设X为向量空间，一个随机赋范空间(简称RN空间)是指一个三元序组(X,μ,T), 其中，T是连续的t范数，映射μ:X→D+满足

1)μx(t)=H0(t) ⟺x=0, 对∀t>0成立；

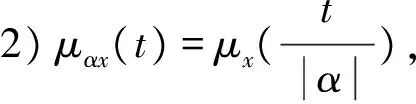
3)μx+y(t+s)≥T(μx(t),μy(t))， 对∀x,y∈X,t,s≥0成立．

定义3[16]设(X,μ,T)是RN空间，

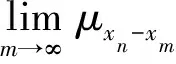
3) 若RN空间(X,μ,T)上的每一个Cauchy列都收敛，则称(X,μ,T)是完备的RN空间．

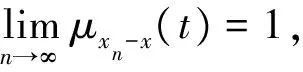
以下为本研究所用到的几种数学符号的表示：Mn(X)为X上所有n×n矩阵的集合；ej∈M1,n()为第j个分量为1，其余分量为0；Eij∈Mn()为第(i,j)个分量为1，其余分量为0；Eij⊗x∈Mn(X)为第(i,j)个分量为x， 其余分量为0．注意，此处Mn,m()上的范数为算子范数，具体定义参考文献[1]．

类似于矩阵赋范空间的定义[1]，给出矩阵随机赋范空间的定义．

定义5设X是向量空间， (Mn(X),μ(n),T)为定义在上的RN空间．

1) 若对∀A∈Mn(表示所有元素为X上零元素的矩阵，有

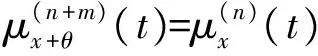
2) (X,{μ(n)},T)称为完备的矩阵RN空间，当且仅当(X,μ,T)为完备的RN空间并且满足(X,{μ(n)},T)为矩阵RN空间．

本研究主要以t范数为TM的情况为例，讨论矩阵随机赋范空间上函数方程的Ulam稳定性．设E和F是向量空间，映射h:E→F， 定义

hn:Mn(E)→Mn(F)

为hn([xij])=[h(xij)]， 其中， [xij]∈Mn(E)．

引理6设(X,{μ(n)},TM)为定义在上的矩阵RN空间，则

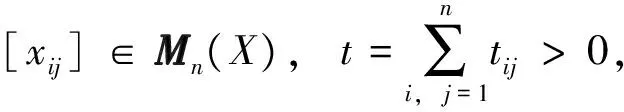
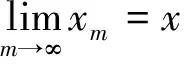
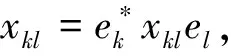
2 函数方程(1)在矩阵随机赋范空间的Ulam稳定性

设X为实的向量空间，Y为完备的矩阵RN空间. 利用RADU[9]给出的不动点方法证明方程(1)在矩阵RN空间上的稳定性. 在这之前,首先给出广义距离空间的定义,它是指一个非空集合S, 并在其上定义的一个二元映射d:S2→[0,∞), 对∀x,y,z∈S， 满足： ①d(x,y)=0 ⟺x=y； ②d(x,y)=d(y,x)； ③d(x,y)≤d(x,z)+d(z,y). 则称d是广义距离，称(S,d)是广义距离空间，在广义距离空间上有下述的不动点定理.

引理7[17]设(S,d)是完备的广义距离空间，J:S→S是严格压缩映射，即存在正数L<1，使对任意的x,y∈S， 都有d(Jx,Jy)≤Ld(x,y)， 则对每个固定的x∈X， 要么对任意负整数n， 有d(Jnx,Jn+1x)=+∞成立；要么存在某个非负整数n0， 使得

1)当n≥n0时，d(Jnx,Jn+1x)<∞；

2)序列{Jnx}收敛于J中不动点y*；

3)y*是集合S′={y∈S|d(Jn0x,y)<∞}中的唯一不动点；

对于映射f:X→Y， 算子Df:X2→Y， 及算子Dfn=Mn(X)2→Mn(Y)， 记

Df(a,b)=4[f(3a+b)+f(3a-b)]-12[f(2a+b)+f(2a-b)]+12[f(a+b)+f(a-b)]-f(2b)+8f(b)-30f(2b)+192f(a)

Dfn([xij],[yij])=4[fn(3[xij]+[yij])+fn(3[xij]-[yij])]-12[fn(2[xij]+[yij])+fn(2[xij]-[yij])]+12[fn([xij]+[yij])+fn([xij]-[yij])]-fn(2[yij])+8fn([yij])-30fn(2[yij])+192fn([xij])

其中，a,b∈X,x=[xij],y=[yij]∈Mn(X)．

定理8设映射φ1:X2→[0,∞)满足存在实数α， 0<α<1， 使得对任意的a,b∈X， 有

(2)

f:X→Y为一个偶映射，使f(0)=0， 满足对所有的x=[xij],y=[yij]∈Mn(X)， 有

(3)

则存在唯一的4次映射Q:X→Y满足对所有的x=[xij]∈Mn(X)， 有

(4)

【证】 在式(3)中，假设当(i,j)≠(s,t)时，有xij=0,yij=0， 则

(5)

令xst=0， 用xst表示yst， 有

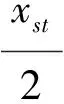
(6)

考虑集合E={g:X→Y,g(0)=0}， 在E上定义广义度量d

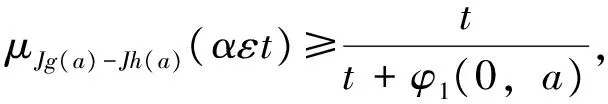
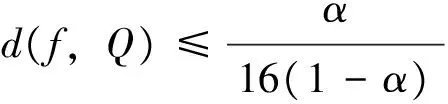
(7)

在式(5)中，用2-lxst代替xst， 2-lyst代替yst， ∀t>0， 有

μ16lDf(2-lxst,2-lyst)(t)=μDf(2-lxst,2-lyst)(16-lt)≥

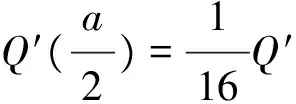
由引理6及不等式(7)得

μfn([xij])-Qn([xij])(t)≥

对∀x=[xij]∈Mn(X)成立，定理得证．

定理9映射φ2:X2→[0,∞)满足存在实数α， 0<α<1， 且使得对任意的a,b∈X， 有

(8)

f:X→Y为个奇映射，使f(0)=0， 满足对所有的x=[xij],y=[yij]∈Mn(X)， 有

(9)

μfn([xij])-Qn([xij])≥

(10)

【证】在式(8)中，当(i,j)≠(s,t)时， 有xij=0,yij=0， 则

(11)

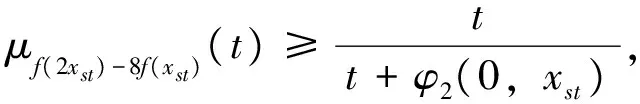
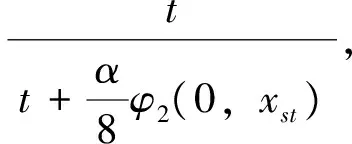
(12)

类似前面讨论,可证明存在唯一的3次映射C:X→Y满足不等式(10).

定理10设映射φ:X2→[0,∞)满足存在实数α, 0<α<1, 且使得对任意的a,b∈X， 有

(13)

f:X→Y满足f(0)=0， 且对所有的x=[xij]，y=[yij]∈Mn(X), 有

(14)

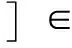
μfn([xij])-Qn([xij])-Cn([xij])≥

(15)

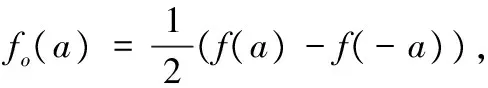
显然定理8和定理9的条件满足，从而由定理8和定理9的证明过程可知，存在唯一的4次映射Q及唯一的3次映射C分别满足

从而

μf(a)-Q(a)-C(a)(t)=μfe(a)-Q(a)+fo(a)-C(a)(t)≥

从而由引理6及上式可知

μfn([xij])-Qn([xij])-Cn([xij])(t)≥

结 语

本研究在随机赋范空间和矩阵赋范空间的基础上，给出了矩阵随机赋范空间的定义，并讨论了其上的一些性质，通过对这些性质的分析，进一步探讨了其上混合型函数方程的稳定性问题，回答了矩阵随机赋范空间上函数方程的稳定性问题，给出了一般的讨论方法．对进一步讨论矩阵随机赋范空间上其他类型函数方程的稳定性问题有借鉴．

引文：宋爱民, 李跃武. 矩阵随机赋范空间上函数方程的Ulam稳定性[J]. 深圳大学学报理工版，2018，35(1)：99-104.

/

[1] RUAN Z J. Subspaces of C*-algebras[J]. Journal of Functional Analysis, 1988, 76(1): 217-230.

[2] EFFROS E G, RUAN Z J. On approximation properties for operator spaces[J]. International Journal of Mathematics, 1990, 1(2): 163-187.

[3] ULAM S M. Problem in modern mathematics[M]. New York (USA): John Wiey & Sons, 1940.

[4] HYERS D H. On the stability of the linear functional equation[J]. Proceedings of the American Mathematical Society, 1941, 72(2): 222-224.

[5] RASSIAS T M. On the stability of the linear mapping in Banach spaces[J]. Proceedings of the American Mathematical Society, 1978, 72(2): 297-300.

[6] SHEN Yonghong, CHEN Wei. Laplace transform method for the Ulam stability of linear fractional differential equations with constant coefficients[J]. Mediterranean Journal of Mathematics, 2017, 14(1): 25.

[7] ZADA A, ALI W, FARINA S. Hyers-Ulam stability of nonlinear differential equations with fractional integrable impulses[J]. Mathematical Methods in the Applied Sciences, 2017, 40(15): 5502-5514.

[8] MOHIUDDINE S A, RASSIAS J M, ALOTAIBI A. Solution of the Ulam stability problem for Euler-Lagrange-Jensen k-quintic mappings[J]. Mathematical Methods in the Applied Sciences, 2016, 30(2): 305-312.

[9] RADU V. The fixed point alternative and the stability of functional equations[J]. Fixed Point Theory, 2003, 4(1): 91-96.

[10] LEE J R, SHIN D Y, PARK C. Hyers-Ulam stability of functional equations in matrix normed spaces[J]. Journal of Inequalities and Applications, 2013, 2013: 22.

[11] PARK C, LEE J R, SHIN D. Functional equations and inequalities in matrix paranormed spaces[J]. Journal of Inequalities and Applications, 2013, 2013: 198.

[12] 宋爱民. 矩阵拟范空间上函数方程的Ulam稳定性[J]. 数学进展, 2016, 45(5): 747-754.

SONG Aimin. The Ulam stability of functional equation on matrix quasi-normed spaces[J]. Advances in Mathematics (China) , 2016, 45(5):747-754.(in Chinese)

[13] SONG Aimin. The Ulam stability of functional equation on matrix intuitionistic fuzzy normed spaces[J]. Journal of Intelligent & Fuzzy Systems, 2017, 32(1): 629-641.

[14] GORDJI M E, EBADIAN A, ZOLFAGHARI S. Stability of a functional equation deriving from cubic and quartic functions[J]. Abstract and Applied Analysis, 2009, 2008(3/4): 491-502.

[15] SCHWEIZER B, SKLAR A. Probabilistic metric spaces[J]. Probability Theory & Related Fields, 1983, 26(3):235-239.

[16] SERSTNEV A N. The notion of random normed space[J]. Doki Acad Nauk Ussr, 1963, 4(2):280-283.

[17] PARK C, KIM J H. The stability of a quadratic functional equation with the fixed point alternative[J]. Abstract and Applied Analysis, 2014, 2009(1): 25-34.