月地双基SAR成像的快速后向投影算法研究
2018-01-15,,,
,,,
1. 中国航天科工二院 北京无线电测量研究所,北京 100854 2. 西安电子科技大学 雷达信号处理国家重点实验室,西安 710071 3. 中国人民解放军63610部队,库尔勒 841001
随着中国月球探测事业的发展,嫦娥工程顺利实施,这标志着中国正在迈入月球探测大国的行列。月球资源具有巨大的战略价值,是人类社会长期可持续发展的重要支撑;月球是深空探测的的前哨站和转运站,是人类探测宇宙、进行深空探测的重要基础[1]。在地球科学应用方面,为满足对全球变化的大尺度观测能力的需求,月基对地观测[2]的概念应运而生。月球作为地球天然的卫星,其独特的性质可为地球的大范围长时间观测提供平台[3-5],这是普通星载合成孔径雷达(Synthetic Aperture Radar,SAR)[6-10]所不具备的优越条件。
由于月基单站SAR的双程作用距离远,回波信噪比低。针对这个问题,本文对月地双基SAR工作模式进行研究。月地双基SAR的工作原理是将发射天线置于月球表面,用人造地球卫星接收地面回波,这种工作模式的优点是可以降低人造卫星的设计和发射成本,提高人造卫星工作能力和使用寿命,相比于月基单站SAR又可以显著提高信噪比。考虑到月、地、星之间复杂的相对运动会为成像带来困难,本文根据月、地、星的几何关系建立平面直角模型,考虑到由轨道弯曲引入的模型误差,分析精确的回波二维频谱。
现有的双基SAR二维频谱分析方法有LBF[11]法、级数反演法(Method of Series Reversion,MSR)[12]及一系列衍生方法[13-14]等,本文基于MSR原理引入模型误差,给出精确回波二维频谱表达式。在此基础上提出了一种基于快速后向投影(Back Projection,BP)[15]的成像算法,该算法借鉴快速分级后向投影(Fast Factorized Back Projection,FFBP)[16]和频谱融合[17]的处理思路,将传统的频域BP[18]算法通过频域分块和频谱融合方式在满足精确成像的前提下实现运算的快速化。本文最后理论分析了月地双基SAR的信噪比表达式,并通过点仿真试验验证了模型误差分析的正确性及所提出算法的有效性。
1 模型描述
月地双基SAR将发射机置于月球表面,利用卫星接收地球表面的反射回波,模型如图1所示。
月球的自转周期和公转周期是一致的,这为月地双基SAR的长时间观测提供了可能性。但月球的运动十分复杂,除绕地球公转运动外还存在太阳及大行星的摄动作用。地月模型主要参数如表1所示,由于地球与月球的自转周期相差较大,该模型忽略月球相对运动对SAR成像的影响,仅考虑地球自转和卫星接收机的运动。双基SAR回波信号表达式沿用传统双基模型[19]:
wr(·)wa(·)
(1)
式中:t和τ分别为距离快时间和方位慢时间;wr(·)和wa(·)分别为距离窗函数和方位窗函数;RT(τ)和RR(τ)分别为发射和接收信号的斜距历史;c为光速;α为发射信号调频率;fc为信号中心频率。在这个模型中,可以假定地球相对静止,月面发射天线和卫星接收天线相对于地面目标的相对运动速度分别为vT和vR,令发射和接收天线的斜视角为θsqT和θsqR,并假设月球轨道和卫星轨道在同一个平面内,则斜距历史RT(τ)和RR(τ)可以表示为:
式中:RsT和RsR分别为发射天线和接收天线在零时刻到目标点的斜距。通过分析式(1)的二维频谱,可以在二维波数域进行距离脉压及距离徙动校正,最后用方位匹配滤波实现方位向聚焦。但卫星和月球的运行轨道是椭圆形轨道,并且存在月球天平动的影响,而式(2)和式(3)建立的基础是平面直角模型,这会为模型引入误差。综合上述因素,会导致斜距历史产生误差ΔR,体现为一个受ΔR扰动的回波信号,如式(4)所示。这里需要说明的是,扰动量ΔR在实际应用中是一个已知量,因为根据已知的月球和卫星轨道参数,可以精确求解以场景任一点为参考点的回波斜距历程,其中包含了月球天平动和章动等复杂运动,与式(2)和式(3)建立的直角模型进行比较即可求得扰动量ΔR,并且扰动量ΔR在成像场景中是一个空变量。本文将在该模型下分析含空变误差ΔR的精确二维频谱表达式,从而指导对回波信号的精确补偿。
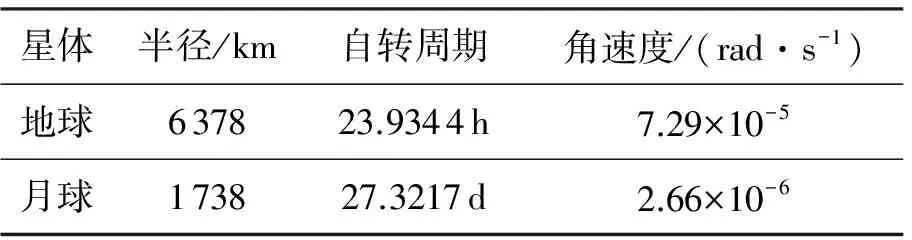
表1 地月模型主要参数Table 1 Main parameters of earth-moon model
2 精确的二维频谱分析
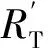
实现精确成像的前提条件是得到回波信号的精确二维频谱,这需要考虑ΔR对回波信号二维频谱的影响,由于ΔR是一个空变量,对于地表P点,可以将ΔR展开为三阶多项式:
式中:p1,p2,p3为展开系数。同时将斜距历史R(τ)=RT(τ)+RR(τ)在τ=0处进行泰勒展开,保留至三阶多项式得到[19]:
其中,
对式(4)进行距离向Fourier变换,得到距离频域-方位时域表达式为:
(12)
式中:fr为距离向波数谱;Wr(·)为信号在频域中的距离向包络。第一个相位项表示斜距历史的包络和相位,第二个相位项是距离脉压因子。将式(5)~(11)带入式(12),并对回波进行距离脉压,通过方位Fourier变换可以得到距离脉压信号的二维频域表达式:
s′(fr,τ*)·exp(-j2πfaτ*)
(13)
由驻定相位原理(Method Of Stationary Phase,POSP)可知,需要求解式(14)方程以得到驻相点τ*:
其中,令l1=k1+p1,l2=k2+p2,l3=k3+p3。令:
则根据文献[12]中的级数反演法(Method of Series Reversion,MSR),驻相点τ*可以表示为关于y的二次多项式:
将式(16)带入式(13),可以得到解析表达的距离脉压信号二维频谱:
s(fr,fa)=Wr(·)Wa(·)·
式中:Wa(·)为信号在频域中的方位向包络;


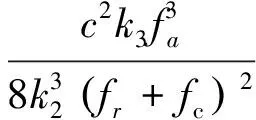

s(τ,fa)=wr(·)Wa(·)exp{-j2π(θ0fc+
式中:(x,y)为成像点的位置坐标,方位匹配滤波2相位因子Φ中包含误差ΔR的影响。由于月地双基SAR的发射、接收天线不同轨,因此回波信号不具备方位平移不变性,因此成像网格内各点对应的λ的方位空变性是需要考虑的因素。频域BP法[18]通过对成像网格内各点计算与其精确匹配的方位滤波器可实现精确成像,但其运算量很大,本文研究通过频域子孔径BP成像及频谱融合的方法实现了算法的快速化。
3 频域子孔径BP算法及频谱融合
传统频域BP算法[18]需要计算成像网格内所有点的方位匹配滤波函数,并依次进行相干积累,这个过程为成像带来巨大的运算量:
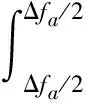
exp[j2πΦ(fa,x,y)]dfa
(19)
通过FFBP的处理思想,利用分解和融合可以实现成像的快速化。算法的初始阶段将方位波数域数据按一定比例划分为若干子块,并划分粗成像网格(xsub,y),在划分的过程中需要对粗成像网格的间隔进行限制,即采样率需要大于方位频域子块的带宽。对于第u个子孔径,方位波数谱中心为fau,则(xp,y)点回波信号通过方位匹配滤波器组后的输出结果:

exp{jΦ[fa,xsub,y]}dfa≈
式中:fa∈[-Δfa/2,Δfa/2]为方位子块波数谱表达式,Δfa为方位波谱宽度;Su(xsub,y)为第u个子孔径在粗成像网格成像结果的时域表达式,下一个步骤中算法将各子孔径的成像结果在方位波数域进行拼接,实现方位波数谱的融合。对式(19)进行方位Fourier变换,得到第u个子块的方位频谱为:
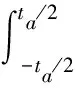
(21)
算法的最后阶段将各子块数据在方位波数域进行融合,这个过程是通过循环移位和拼接实现的。由式(21)可知,第u个子图像的方位波数谱中心在fau处,而波数谱宽度为Δfa,因此谱会存在折叠。需要将该孔径的谱循环移位至fau相对于全部谱宽Δfa中的位置,各子图像依次进行移位和拼接,可以得到完整的波数谱,这个过程如图3所示。最后通过方位逆Fourier变换,可以得到全分辨的成像结果。
4 信噪比分析
根据信噪比[20]:
(22)
式中:Pavg为平均发射功率;G为天线增益;λ为波长;σ为目标截面积;R为雷达到目标的距离;Ls为系统损失;k为玻尔兹曼常数;T0为标准温度;F为噪声系数;ta为合成孔径时间。对于SAR而言,合成孔径时间ta表示为:
式中:ω为平台角速度;δa=Dcosθsq/2为方位向分辨率;D为天线孔径长度;θsq为斜视角。目标截面积σ表示为:
式中:σ0为地面目标的归一化后向散射技术;δr=c/2B为距离分辨率;c为光速;B为信号带宽;θi为波束入射角。则信噪比为:
对于月基单站SAR,信噪比表达式为:
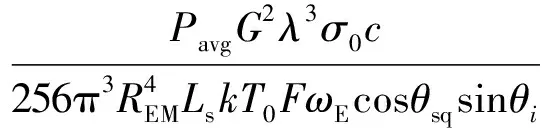
式中:REM为地月距离;ωE为地球自转角速度。
对于月地双基SAR,信噪比表达式为:
式中:RS为卫星与散射点的距离;ωS为卫星相对于目标点的角速度;θsqR为接收天线的斜视角。在式(27)中,地月距离REM为一个较大的量。对于月基单站SAR,信噪比与REM的四次方成反比,而月地双基SAR的信噪比仅与REM的二次方成反比。可见与月基单站模式相比,月地双基模式可以很大程度上改善回波信噪比。
5 合成孔径时间分析
由于月地双基SAR的合成孔径时间主要由卫星决定,因此可以根据卫星参数进行合成孔径时间的计算。令天线尺寸为D,则天线方位向波束宽度为:
接收回波信号的卫星高度为hs,则卫星运动的角速度为:
式中:G0为万有引力常数;M为地球质量;Re为地球半径。则合成孔径时间T的表达式为:
6 仿真试验
本节通过点目标仿真对本文算法进行验证,仿真参数如表2所示,发射信号选用X波段,接收卫星轨道高度设为1 000 km,根据开普勒方程计算得到卫星的运动速度为7 350 m/s。月球到地心的距离约为384 400 km,假设仅考虑地球自转,月球相对于地球的运动速度约为27 634 m/s。

表2 仿真参数Table 2 Simulation parameters
对于场景中心点,补偿轨道弯曲前后的距离徙动校正对比结果如图4所示。图4(a)为平面模型假设下的结果,可以发现距离脉压信号存在残余的弯曲,图4(b)为本文算法校正后的结果,不存在跨距离单元的徙动。图5为点目标成像的对比结果,由于存在残余包络和相位误差,图5(a)的图像无法聚焦,图5(b)中本文算法可以实现点目标的聚焦。图5给出的是场景中心附近点的成像结果,因此模型误差ΔR的方位空变性并不明显。为了说明算法对方位空变误差的补偿效果,图6给出了方位向50 km处点目标的一维方位脉冲响应函数对比,由于补偿了ΔR的方位空变性,本文算法的方位聚焦效果优于仅补偿场景中心点的算法。
7 结束语
针对月地双基SAR的工作模式,本文详细分析回波的精确二维频谱,提出了一种基于快速后向投影的成像算法。通过分析可知月地双基SAR信噪比与地月距离的二次方成反比,相对于月基单站SAR有显著提升。通过X波段点目标仿真验证了该方法可以补偿由轨道弯曲引起的方位空变模型误差,说明了该方法对处理月地双基SAR成像问题的有效性。
References)
[1] 欧阳自远. 我国月球探测的总体科学目标与发展战略[J]. 地球科学进展,2004,19(3): 351-358.
OUYANG Z Y. Scientific objectives of Chinese lunar exploration project and development strategy[J]. Advances in Earth Science,2004,19(3): 351-358(in Chinese).
[2] 郭华东,傅文学,李新武,等. 全球变化科学卫星概念研究[J]. 中国科学: 地球科学,2014,44: 49-60.
GUO H D,FU W X,LI X W,et al. Research on global change scientific satellites[J]. Science China: Earth Sciences,2014,44: 49-60(in Chinese).
[3] 郭华东,丁翼星,刘广,等. 面向全球变化探测的月基成像雷达概念研究[J]. 中国科学: 地球科学,2013,43: 1760-1769.
GUO H D,DING Y X,LIU G,et al. Conceptual study of lunar-based SAR for global change monitoring[J]. Science China: Earth Sciences,2013,43: 1760-1769(in Chinese).
[4] 丁翼星,郭华东,刘广. 面向全球变化探测的月基对地观测覆盖性能分析[J]. 湖南大学学报(自然科学版),2014,41(10): 96-102.
DING Y X,GUO H D,LIU G. Coverage performance analysis of earth observation from lunar base for global change detection[J]. Journal of Hunan University (Natural Sciences),2014,41(10): 96-102(in Chinese).
[5] MOCCIA A,RENGA A. Synthetic aperture radar for earth observation from a lunar base: performance and potential applications[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010,46(3): 1034-1051.
[6] 邓云凯,赵凤军,王宇. 星载 SAR 技术的发展趋势及应用浅析[J]. 雷达学报,2012,1(1): 1-10.
DENG Y K,ZHAO F J,WANG Y. Brief analysis on the development and application of spaceborne SAR[J]. Journal of Radars,2012,48(1): 56-57(in Chinese).
[7] 李财品,何明一,朱雅琳,等. GEO SAR长合成孔径时间弯曲轨迹成像试验[J]. 中国空间科学技术,2015,35(4): 17-22.
LI C P,HE M Y,ZHU Y L,et al. Imaging experiment with long integrated time and curved trajectory for geosynchronous obit SAR[J]. Chinese Space Science and Technology,2015,35(4): 17-22(in Chinese).
[8] BAO M,XING M D,LI Y C. Chirp scaling algorithm for GEO SAR based on four-order range equation[J]. Electronic Letters,2012,48(1): 56-57.
[9] 梁健,张润宁,包敏凤. 天基视频SAR系统设计及成像算法研究[J]. 中国空间科学技术,2016,36(6): 22-28.
LIANG J,ZHANG R N,BAO M F. Research on spaceborne video SAR system design and image formation algorithm[J]. Chinese Space Science and Technology,2016,36(6): 22-28 (in Chinese).
[10] 陶满意,纪鹏,黄源宝,等. 星载SAR辐射定标及其精度分析[J]. 中国空间科学技术,2015,35(5): 64-70.
TAO M Y,JI P,HUANG Y B,et al. Radiometric calibration and accuracy analysis based on spaceborne SAR[J]. Chinese Space Science and Technology,2015,35(5): 64-70 (in Chinese).
[11] LOFFELD O,NIES H,PETERS V,et al. Models and useful relations for bistatic SAR processing[J]. IEEE Transactions on Geoscience and Remote Sensing,2004,42(10): 2031-2038.
[12] NEO Y L,WONG F H, CUMMING I G. A two-dimensional spectrum for bistatic SAR processing using series reversion[J]. IEEE Geoscience and Remote Sensing Letters,2007,4(1): 93-96.
[13] NATROSHVILI K,LOFFELD O,MAYA A,et al. Focusing of general bistatic SAR configuration data with 2-D inverse scaled FFT[J]. IEEE Transactions on Geoscience and Remote Sensing,2006,44(10): 2718-2727.
[14] NEO Y L,WONG F H, CUMMING I G. A comparison of point target spectra derived for bistatic SAR processing[J]. IEEE Transactions on Geoscience and Remote Sensing,2008,46(9): 2481-2492.
[15] MENG D D,HU D H,DING C B. Precise focusing of airborne SAR data with wide aperture large trajectory deviations: a chirp modulation back-projection approach [J]. IEEE Transactions on Geoscience and Remote Sensing,2015,53(5): 2510-2519.
[16] ULANDER L M H,HELLSTEN H,STENSTROM G. Synthetic aperture radar processing using fast factorized back-projection[J]. IEEE Transactions on Aerospace and Electronic Systems,2003,39(3): 760-776.
[17] ZHANG L,LI H L,QIAO Z J,et al. A fast BP algorithm with wavenumber spectrum fusion for high-resolution spotlight SAR imaging[J]. IEEE Geoscience and Remote Sensing Letters,2014,11(9): 1460-1464.
[18] LI Z,WANG J,QING H L. Frequency-domain backprojection algorithm for synthetic aperture radar imaging[J]. IEEE Geoscience and Remote Sensing Letters,2015,12(4): 905-909.
[19] 熊涛. 双基SAR成像算法研究[D]. 西安: 西安电子科技大学,2012.
XIONG T. Study on imaging algorithms for bistatic SAR[D]. Xi′an: Xidian University,2012(in Chinese).
[20] SKOLNIK M I. 雷达手册[M]. 王军,等译.北京: 电子工业出版社,2003.
