Methods of spacecraft impulsive relative hovering and trajectory safety analysis
2018-01-15CHENGBoYUANJianpingQIANYingjingMAWeihua
CHENG Bo, YUAN Jianping, QIAN Yingjing, MA Weihua
1.School of Astronautics, Northwestern Polytechnical University, Xi′an 710072, China 2.Beijing Institute of Astronautical Systems Engineering, Beijing 100076, China 3.National Key Laboratory of Aerospace Flight Dynamics, Xi′an 710072, China
With the continuous improvement of human space activities, the complexity of the space missions ongoing and planed has been increased. The structure of the spacecraft has becoming complicated, and the spacecraft capability has been increased. In such a situation, scholars put their eyes on the stable operation of spacecraft on orbit. Therefore, the need for on-orbit service is extremely urgent, such as refueling, maintenance, replacing, updating and other servicing operations of spacecraft[1-2].
Spacecraft relative hovering is viewed as a significant part of the on-orbit service technology. By using the force and moment, a relative hovering mission can maintain the relative distance of active spacecraft respect to the target spacecraft in a specified reference coordinate frame[3].
There have been some literatures about the relative hovering technique. Scholars studied the hovering problems near asteroids and between two spacecraft[4]. Zeng et al deduced the dynamic equations of hovering flight over elongated asteroids for solar sails with the ability of active sail areas control, and the feasible hovering detection area was analyzed by using the dynamic model[5]. Wang and Xu proposed a feedback control law for the orbit-attitude hovering of a spacecraft in the body-fixed frame of a uniformly rotating asteroid based on the non-canonical Hamiltonian structure. Using this control law, the artificial equilibrium can be created at the desired hovering position-attitude and be successfully stabilized in the Lyapunov sense[6]. An adaptive sliding mode control scheme, which can be used for autonomous body-fixed hovering maneuvers of a rigid spacecraft in the proximity of an asteroid involving uncertainties and time-varying external disturbances, was proposed by Lee and Vukovich to guarantee the asymptotic stability of states for position and attitude stabilization[7]. Dang established a precise analytic model of hovering control with the influence ofJ2perturbation, both in circular and elliptical reference orbit. With the models, the maximum and minimum force positions were determined, and the formula for calculating fuel consumption was derived[8]. Zhang et al analyzed the hovering acceleration inR-bar andV-bar direction and obtained an analytical form of the control force and velocity increment of hovering[9]. The works above solved the problems of modeling and control of spacecraft hovering efficiently. However, most of the dynamic models in previous works were based on the continuous thrust, which brought difficulties to the propulsion system of active spacecraft. Therefore, some scholars based their studies on the impulsive thrust orbit control method.
Based on the Clohessy-Wiltshire equations, Pan studied the impulse control strategy and the entry method of drip-drop hovering orbit[10]. Rao et al presented the absolute orbit relationship between the target and mission spacecraft, and described the configuration of the hovering orbit in and out of the target spacecraft orbital plane based on the relative orbital elements. An interval impulse control strategy for hovering formation was derived in their work, which could make the mission spacecraft remain at a specified position to the target spacecraft for a long time[11]. Using the open-loop, interval impulse control method, the works above reduced the difficulty of implementation of hovering mission, but their control schemes were only fit for the circular and near circular reference orbit hovering.
For the closed, long-term hovering study, the hovering trajectory safety should be pay more attention to avoid the collision between the two spacecraft. Based on the collision probability, some scholars studied the trajectory safety of relative motion between two space objects[12-14].
Based on the analytic solutions of Tschauner-Hempel equations (T-H equations) and its state transition matrix form, a method of spacecraft hovering is proposed in this work. This method can be used for mission design of circular and elliptical reference orbit hovering. The velocity pulse calculated by the method would be easier for the propulsion system to control the relative hovering. The true anomaly intervals for orbit maneuver are optimized by using the nonlinear mathematical programming method, which would reduce the mean position deviation of the hovering. The hovering trajectory safety analysis method presented in this paper establishes an approximate calculation model of collision probability, which quantifies the collision risk of hovering.
The numerical simulations in this paper show that, the method can be used to design the hovering mission on circular and elliptical reference orbit, under certain precision. The local optimal solution of the mean position deviation can be obtained by calculating with the optimized true anomaly intervals. The maximum collision probability and the minimum relative distance of the two spacecraft appear nearly at the same time. Moreover, the smaller the relative distance is, the larger the collision probability.
1 Relative motion modeling
The earth-centered inertial coordinationO-XYZ(ECI) and a rotating orthogonal coordinate systemo-xyz(TCO) with its origin at the centre of the mass of target spacecraft are selected to describe the relative hovering motion.
As illustrated in Fig.1, the origin of ECI is located at the centre of the earth, theXaxis is in the equatorial plane, pointing to the direction of vernal equinox, theYaxis is also in the equatorial plane, perpendicular to theXaxis, and theZaxis completing the right-handed frame of the system. Unit vectors in the direction of each axis of the TCO coordinates are defined as follows:
WhereRtis the position vector of target spacecraft;htis the orbital angular momentum of reference orbit defined by
In the TCO coordinate frame, the relative motion dynamical equations (T-H equations) are established with the true anomalyθas a variable[15-16].

Fig.1 Coordinate frame for hovering spacecraft
Where(·)′means derivation respect to the true anomalyθ;eis the eccentricity of the reference orbit;ξ=1+ecosθ; the control and interference acceleration vectorais defined by
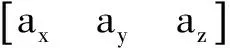
Eq.(1) are non-homogeneous differential equations when the acceleration vectorais an arbitrary time function. It is hard to obtain the analytic solutions of Eq.(1)[17]. Considering that the active spacecraft is free from external force, the variables of Eq.(1) can be changed as follows:
We can obtain the analytic solutions of T-H equations[18]:
The elements ofΦθare as below:
WhereJ=(h/p2)(t-t0);c=ξcosθ;s=ξsinθ;c′=-sinθ-esin(2θ);s′=cosθ+ecos(2θ).
Expressing the analytic solutions of T-H equations in a state transition matrix notation, we obtain:
Furthermore, we obtain:
Inserting Eq.(5) into the notation ofΦθ, the determinant ofΦθ0:



2 Impulsive hovering method
Spacecraft hovering is to apply the corresponding control force, so that the active spacecraft position, respect to the target spacecraft, remains unchanged. The relative velocity and relative acceleration of the active spacecraft are equal to zero in the TCO coordinate frame[3]:
2.1 Velocity increment of impulsive hovering
For the troubles of continuous thrust bring to the control and propulsion system of active spacecraft, the relative acceleration control in Eq.(8) is difficult to achieve. Therefore, we consider using impulsive control method to keep the relative position unchanged within a certain period. If the deviation is small enough, or meets the engineering requirements, it can be considered that the two spacecraft have achieved a continuous relative hovering approximately.

Every block in Eq.(9) is three dimensional matrix.



Recall that the velocity calculated by Eq.(12) should be converted into the true values using Eq.(2).
2.2 Energy consumption analysis
Using the impulsive orbital maneuvering method, the active spacecraft transfers from the hovering point through a cycle back to the previous point. For a short enough control period, the impulsive hovering method can be considered as the discrete form of the continuous thrust method. Furthermore, for a minimal control period, the velocity increment of impulsive hovering method should be approximately similar to that of the continuous thrust hovering. Therefore, with the continuous thrust hovering method, the trends of the velocity of the active spacecraft at different hovering points are the same as those of the impulsive one. The control accelerations of continuous thrust hovering method are expressed as follows:

Eq.(13) shows that, the control accelerations are proportional to the relative position. Moreover, the hovering motion perpendicular to the orbital plane is decoupled from the one in the orbital plane. We can obtain the velocity increment by integrating Eq.(13):

The velocity increment of hovering during one reference orbit period can be calculated by Eq.(14).
2.3 Optimization of impulsive hovering maneuver

Assuming the true anomaly intervals of one reference orbit period are
Δθi,i=1,2,…,N
WhereNis the pulse number.
The mean position deviation of the multi-pulse hovering can be calculated as follows:
Δθican be optimized using the mathematical programming method[21-22].
The optimization can be described as below:

The problem described by Eq.(16) is to find a minimum of constrained nonlinear multivariable function. The sequential quadratic programming method and trust region method can be used to solve this problem.
2.4 Impulsive thrust model
Idealizing the impulsive working mode of orbital maneuvering engine system as a finite thrust model[23], we can calculate the velocity increment using the equation below:
Fig.2 illustrates the impulsive thrust mode of engine.

Fig.2 Impulsive thrust model of engine
In Fig.2,τrepresents the rise time and the drop-out time of the impulsive thrust,Tis the steady-state working time andFmaxis the deputy of ultimate thrust. The equivalent thrust of engine can be calculated:
We can obtaintby donating the velocity increment into Eq.(17). If the equivalent thrust is on the small side, a longer working time is required to allow the active spacecraft to obtain the velocity increment for hovering. However, during establishing the velocity increment, the relative states of the two spacecraft will change greatly, which will affect the accuracy of the orbit maneuver. Therefore, it is necessary to select an appropriate engine for improving the accuracy and stability of the impulsive hovering.
3 Trajectory safety analysis
Based on the analytic solutions of T-H equations and its state transition matrix form, the open-loop control method of spacecraft relative hovering is introduced in the former section. Comparing with the continuous thrust control method, the impulsive one is applicable for the engineering application. It is noteworthy that linearization and approximation are introduced in the derivation of the relative motion dynamic equations. Furthermore, the method takes no consideration of the gravitational perturbation. Therefore, this method induces some targeting error, especially for closed, long-term hovering, which could lead to the active spacecraft colliding with the target one. In this section, we discuss the trajectory safety of hovering based on the collision probability.


WhereEis expectation operator. Using Eq.(19) we can obtain the covariance matrix of relative states for arbitrary time.




Two assumptions are introduced for the hovering motion collision probability calculation:
1) The position state of the target spacecraft is a certain amount, and the uncertainty of the relative position of the two spacecraft is attached to the active spacecraft.
2) The structure of the spacecraft is shaped as an envelope ball, and the envelopes of the two spacecraft are combined into a total envelope ballV, whose centre is the centroidal of target spacecraft and whose radius is the sum of the two radiuses.
According to the assumptions above, the collision probability of relative hovering is equivalent to the integration of probability density of Eq.(20). If the total envelop ball has uniform probability density, the integration can be simplified to be an algebraic operation:

(21)
For the relative hovering trajectory safety analysis, the prediction of the collision probability can be obtained by Eq.(21). If the prediction is greater than the thresholdPalarm, orbital maneuver should be imposed for reducing the collision probability.
4 Numerical verification
The numerical simulations are applied to verify the correctness of the impulsive relative hovering method and the trajectory safety analysis. Simulation conditions are summarized in Table 1.

Table 1 Initial condition of target spacecraft
The relative position and velocity at initial time areρ0(km) andv0(km/s) respectively:
The hovering point and the initial relative position are set to be the same.
4.1 Spacecraft impulsive hovering
The fmincon function of Matlab is used to optimize the true anomaly intervals Δθi. The number of impulse (IN) in one orbital period is 6, 9 and 12 respectively. The initial optimization value of the anomaly intervals are equal.

Table 2 Optimization of the true anomaly intervals
The simulation results in Table 2 show that, as the impulse number increases the mean position deviation reduces. The optimization method applied in this paper is helpful to increasing the accuracy of hovering. It should be noted that the optimal solution of the nonlinear programming method is probably the local optimal solution. Whether it is the global optimal solution depends on the initial value.
With the optimized true anomaly intervals shown in Table 2, Fig.3 compares the hovering trajectory. The dotted line represents the case when IN=9, and the solid line shows the case when IN=12.

Fig.3 Trajectories of the impulsive relative hovering
As it is shown in Fig.3, due to the first order linearization and approximation of relative motion model, there are errors between the relative hovering trajectory and the desired hovering point. Meanwhile, the error accumulation of impulsive hovering method also contributes to the deviation.
4.2 Trajectory safety of hovering
In this simulation case, the radius of the total envelope ball is 100 m, and the standard deviations of relative position and velocity are 250 m and 0.3 m/s respectively.The independent relative states obey normal distribution. The diagonal elements of the covariance matrix of relative states distribution at the initial time are the square of the standard deviation of the relative states, and off-diagonal elements are all zeros.
Fig.4 shows the relative distance of two spacecraft under the situation of 8 equal true anomaly intervals during two reference orbit periods. The collision probability during orbital maneuvers is shown in Fig.5.

Fig.4 Relative distance of impulsive relative hovering

Fig.5 Collision probability of impulsive relative hovering
As it is shown in Fig.4, there is a minimum relative distance during every orbital maneuver. The relative position changes during the hovering. At the end of the orbit period, the relative position regresses basically. The collision probability of relative hovering is related to the relative distance.
Fig.5 shows the collision probability of relative hovering. Comparing with Fig.4, during every impulse the relative distance decreases at first and then increases; the collision probability increases and then decreases. The maximum collision probability changes when the minimum relative distance changes. The maximum collision probability and the minimum relative distance appear almost at the same time.
For the spacecraft hovering task design, if the collision probability is greater than the thresholdPalarm, orbital maneuver should be imposed to reduce it to avoid collision.
5 Conclusions
On the consideration of the analytical solutions of T-H equations with its state transition matrix form, a relative hovering method was developed. Using the method of nonlinear mathematical programming, the true anomaly intervals of the hovering impulse were optimized to reduce the mean position deviation. Based on the calculation of collision probability, the method of safety analysis and risk management was proposed.
The numerical simulations show that the relative hovering method introduced in this paper can be used for circular and elliptical reference orbits hovering, which is promising for practical engineering use. Shortening the period of the orbit maneuver pulse can improve the relative hovering. The maximum collision probability and the minimum relative distance appear almost at the same time. Furthermore, the smaller the relative distance is, the larger the collision probability.
[1] CUI N G, WANG P, GUO J F, et al. A review on-orbit servicing[J]. Journal of Astronautics, 2007,28(4):33-39(in Chinese).
[2] CHEN X Q, YUAN J P, YAO W, et al. On-orbit servicing technology of spacecraft[M]. Beijing:China Astronautic Publishing House, 2009:1-22(in Chinese).
[3] YUAN J P, LI J F, HE X S, et al. Relative motion orbit dynamics of spacecraft[M]. Beijing:China Astronautic Publishing House, 2013:482-561(in Chinese).
[4] ZHU Y W. Study on orbital characteristics and control of hovering spacecraft[D]. Changsha: National University of Defense Technology, 2010(in Chinese).
[5] ZENG X Y, GONG S P, LI J F, et al. Hovering flight over elongated asteroids by using solar sails[J]. Journal of Deep Space Exploration,2015,2(1):48-52(in Chinese).
[6] WANG Y, XU S J. Body-fixed orbit-attitude hovering control over an asteroid using non-canonical Hamiltonian structure[J]. Acta Astronautica, 2015,117:450-468.
[7] LEE D, VUKOVICH G. Adaptive sliding mode control for spacecraft body-fixed hovering in the proximity of an asteroid[J]. Aerpspace Science and Technology, 2015,46:471-483.
[8] DANG Z H, WANG Z K, ZHANG Y L. Modeling and analysis of relative hovering control for spacecraft[J]. Journal of Guidance Control and Dynamics, 2014,37(4):1091-1102.
[9] ZHANG J R, ZHAO S G, YANG Y Z. Characteristic analysis for elliptical orbit hovering based on relative dynamics[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013,49(4):2742-2750.
[10] PAN Y. Study on spacecraft relative drip-drop hovering orbit[J]. Spacecraft Engineering, 2014,23(4):13-18(in Chinese).
[11] RAO Y R, HAN C, YIN J F, et al. Method of spacecraft hovering formation design and control[J]. Acta Aeronautica et Astronautica Sinica, 2015,36(7):2361-2371(in Chinese).
[12] XU X L, XIONG Y Q. Analysis of the applicability of collision probability algorithms for nonlinear relative motion[J]. Science China, Physics, Mechanics & Astronomy, 2013,56(5):1041-1046.
[13] SLATER G L, BYRAM S M, WILLIAMS T W. Collision avoidance for satellites in formation flight[J]. Journal of Guidance Control and Dynamics, 2012, 29(5):1140-1146.
[14] BAI X Z, CHEN L. Research on calculational method of collision probability between space objects[J]. Journal of Astronautics, 2008,29(4):1435-1442(in Chinese).
[15] CAO Y H, FAN P C, BAI X Z, et al. Initial error propagation of elliptical orbit based on T-H equation[J]. Chinese Space Science and Technology, 2014, 34(2):28-35(in Chinese).
[16] BAI X Z. Research on orbital prediction error and collision probability of space objects[D]. Changsha: National University of Defense Technology, 2013(in Chinese).
[17] LIU T, ZHAO J. Dynamics of spacecraft[M]. Harbin:Harbin Institute of Technology Press,2003:83-101(in Chinese).
[18] YAMANAKA K, ANKERSEN F. New state transition matrix for relative motion on an arbitrary elliptical orbit[J]. Journal of Guidance Control and Dynamics, 2002,25(1):60-66.
[19] ZHANG A P. Determination and solution of invertible matrix[J]. Journal of Chifeng University,2011,27(3):12-13(in Chinese).
[20] INALHAN G, TILLERSON M, HOW J P. Relative dynamics and control of spacecraft formation in eccentric orbits[J]. Journal of Guidance Control and Dynamics, 2002,25(1):48-59.
[21] YUAN Y X. Nonlinear optimization calculation method[M]. Beijing:Science Press,2008:136-224(in Chinese).
[22] HUANG H X, HAN J Y. Mathematical programming[M]. Beijing:Tsinghua University Press,2006:220-324(in Chinese).
[23] GU L X, GONG C L, HAO B. Design and simulation of KKV control scheme[J]. Journal of Northwestern Polytechnical University, 2007,25(3):402-405(in Chinese).
[24] YANG B H. Spacecraft guidance, navigation and control[M]. Beijing:China Science and Technology Press,2011:51-95(in Chinese).
[25] LIN L X. Space rendezvous and docking technology[M]. Beijing:National Defense Industry Press,1995:108-211(in Chinese).
[26] GOTTLIEB R G, SPONAUGLE S J, GAYLOR D E. Orbit determination accuracy requirements for collision avoidance[C].AIAA/AAS Space Flight Mechanics Meeting. Santa Barbara:AIAA,2001:1105-1121.
[27] ZHU J P. Applied multivariate statistical analysis[M]. Beijing:Science Press,2012:8-26(in Chinese).
(Editor: GAO Zhen)
