化工原理中伯努利方程的教学探讨
2018-01-12秦正龙
秦正龙
(江苏师范大学化学化工学院,江苏 徐州 221116)
流体流动原理不但是流体输送、搅拌、过滤等动量传递过程的理论基础,也是热量传递、质量传递过程中各种单元操作的理论基础,而伯努利方程又是流体流动中最重要、最核心的内容,是贯穿整个化工原理教学过程的重点和难点[1,2]。因此,准确理解和掌握伯努利方程对于学好化工原理显得尤为重要。然而,在实际教学过程中我们发现,学生上课时似乎听懂了,方程也记住了,但遇到实际问题时却又不知从何着手[3]。为此,我们在教学方法上作了一点探索。
1伯努利方程的表达形式
化工原理是化工类各专业重要的专业基础课程,主要研究流体流动、输送、传热、非均相机械分离、传质等单元操作的过程原理、过程计算、设备选型等[4,5],具有较强的工程特性。尤其是对于少学时化工原理的教学,过分强调理论知识和传递知识基础,未必能收到好的教学效果[6]。因此,我们在教学过程中教材上所有公式的推导一律删除不讲,把重点放在加强学生对方程物理意义的理解上,在应用上多挖掘公式的内涵,为学生熟练掌握公式、应用公式奠定基础。
伯努利方程是理想流体在定常态下流动的动力学方程,即在重力场中,同一流管上的任何一个截面处,流体的位能、动能和压强能之和是一个常数。伯努利方程的表达形式主要有四种。

(1)
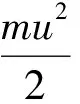
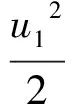
(2)
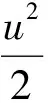

(3)
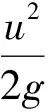

(4)
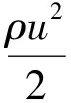
以上四式虽然表达形式不同,表示能量的单位也不同,但其实质是一样的,应用时可灵活选择。
如果令上述四式中的u1=u2=0,则四式均变为:
p2=p1+ρg(z1-z2)
(5)
式(5)即为流体静力学方程。可见,流体静力学方程是伯努利方程的一种特殊形式,同时也说明了“静止是运动的一种特殊形式”这一哲学思想。
2伯努利方程的适用条件
伯努利方程的适用条件在教学过程中是比较容易被忽视的。尽管伯努利方程的推导过程在课堂上没有具体的讲解,但它是在一定条件下得到的,因此,其适用条件必须向学生交待清楚。具体的使用条件[7,8]是:①理想流体作定常流动,在系统中没有其它的吸入和损失。由于流体没有粘性,所以在流动过程中没有摩擦阻力。②流体不可压缩,其密度不随压强变化而变化。液体一般可以认为是不可压缩流体;对于气体,两衡算截面间的压强变化不能超过20%。③流体流动过程中没有热量的加入和引出,流体的温度恒定,内能不变。④作用在流体上的体积力只有重力。
3伯努利方程的解题技巧
3.1 实际流体伯努利方程
由于化工生产中处理的流体都是实际流体,所以在流动过程中使一部分机械能转化为内能,造成机械能的损失。为了保证流体作定常态流动,必须用泵等作功机械给流体补充能量。因此,在截面1流体输入的机械能与输送设备所作的有效功的能量之和一定等于截面2 输出的机械能及两截面之间流体的阻力损失之和,即
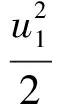
(6)
或

(7)
式(6)、(7)为实际流体伯努利方程,也称机械能守恒方程。其中的hf、Hf分别是单位质量流体、单位重量流体从截面1流到截面2损失的机械能,且满足gHf= hf。We、He依次是单位质量流体、单位重量流体从输送设备获得的机械能,且满足gHe= We。
3.2 伯努利方程的解题要点
在化工原理的“流体流动”和“流体输送设备”两个章节中,有关大型的计算题几乎都要用到伯努利方程,这也是考研的一个重点。如果掌握了伯努利方程的解题技巧,可以大大地简化计算,很快得到结果。其解题要点是:
(1)根据题意,画出过程的示意图,确定衡算范围。
(2)截面的选取。截面的选择一般需要满足以下四点。①截面必须处在流体的均匀流段,在两个截面之间可以是急变流。②截面必须与流体的流动方向垂直,且在两个截面之间流体是连续的。③所求的未知量应在两个截面上或在两个截面之间。④截面上的参数尽可能多是已知的。当然,截面既可选在管道入口、出口的内侧,也可选在管道入口、出口的外侧。如果选择内侧,则计算动能,局部阻力为零;相反,如果选择外侧,则计算局部阻力,动能为零。
(3)基准面的选择。基准面的选取可以是任意的,但必须与地平面平行。一般选择两个截面中低的且通过其中心的面作为基准面。如果截面与基准面不平行,z必须取截面中心与基准面之间的垂直距离。
(4)统一方程中各个物理量的单位。在应用伯努利方程计算前,应把每个物理量的单位都换算成国际单位。特别是压强,除了要用国际单位表示外,其表示方式两边也要统一,要么都用绝对压,要么都用表压,千万不能混合使用。此外,还必须明确,压力表的读数是表压,真空表的读数是真空度;如果截面与大气联通,则该截面上的表压为零;如果截面的面积比管路的横截面积或其他截面的面积大得多,则该截面上流体的流速为零。
4伯努利方程的应用
应用伯努利方程,可以计算流体的流速、流量及流体输送所需要的压头和功率[9,10]。
4.1 确定设备间的相对位置
为了保证管路中一定的液体输送能力,两个设备之间必须要有一定的高度差。高度差小了,液体的流量低;高度差大了,液体的流量高。根据题意,把已知参数代入伯努利方程,即可求出。此类问题通常是求高位槽的高度。
4.2 计算管道中流体的流量
由于流体的流量未知,因此流体流动的摩擦阻力系数也无法获得,只能采用试差法。首先假设一个摩擦阻力系数,然后代入伯努利方程计算流速,再计算雷诺准数,根据雷诺准数和相对粗糙度由莫狄图
查得摩擦阻力系数,如果查得的摩擦阻力系数与假设的摩擦阻力系数相等,则假设成立,流速乘管路的横截面积即为流量。如果查得的摩擦阻力系数与假设的摩擦阻力系数不相等,则重新假设,直到相等为止。
4.3 确定输送设备的有效功率和轴功率
根据伯努利方程,计算出单位质量流体从输送设备处获得的有效机械能,然后乘以流体的质量流量即为输送设备的有效功率,有效功率再除以流体输送设备的效率得到轴功率。据此可以选择适宜的流体输送机械。
4.4 计算管道中流体的压强
通过在已知压强截面与管道中某截面之间列伯努利方程,即可得到某截面上流体的压强,但两个截面之间流体一定要连续。下面通过一个具体的例子来说明。
用一根虹吸管将水从池中吸出,水池液面与虹吸管出口的垂直距离为8 m,管路最高点与水面的垂直距离为2 m,求虹吸管出口处水的流速。已知水温30 ℃,水的密度取1 000 kg/m3,大气压为101.3 kPa,水按理想流体处理。
解:取水池液面为截面1,虹吸管出口为截面2,并以截面2为基准面。则:
p1=p2=0(表压),u1=0,z1=8m,z2=0
将上述参数代入伯努利方程(3),整理得:

绝大部分学生都是这样做的。那么,上述方法对吗?
我们可以作如下分析:首先假设截面1、2之间的流体水是连续的,则应用伯努利方程,可解出虹吸管出口流速为12.52 m/s。
显然,在虹吸管的最高点流体的压强最小。取虹吸管的最高点并与流体流动方向垂直的面为截面3,以截面1为基准面。则:
p1=1.013×105Pa,z1=0m,z3=2m,u1=0,u3= u2=12.52 m/s
将上述参数代入伯努利方程(3),整理得:
p3= p1-(2+8)ρg=101 300-10×1 000×9.8=3 300 Pa
查得30 ℃时水的饱和蒸气压pV为4 242 Pa,显然大于p3,故在最高点3附近流体水发生汽化,此时截面3处的压强不再按伯努利方程的规律变化,而是保持流体的饱和蒸气压pV不变。因此,截面1、2之间的流体水不连续,伯努利方程不适用,虹吸管出口流速为12.52m/s无效。但截面1、3之间的流体是连续的,在截面1、3之间列伯努利方程,得:
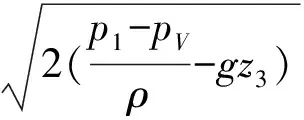

这一习题表面上看是应用伯努利方程求流体的流速,实际上考察的是伯努利方程的使用条件,这一点学生往往容易忽略。
5结 语
有关伯努利方程的教学,绝大部分教师都十分重视方程的理论推导。但我们发现,由于学生的流体力学、高等数学等知识都比较欠缺,因此,往往是教师讲了一节课、写了一黑板,学生还没理出个头绪,反而影响了学生的学习兴趣和对方程的理解。我们直接给出伯努利方程,把重点放在介绍方程中各参数的含义,讲清方程的物理意义,强调方程适当的条件,理清解题的思路,讨论、总结相关计算的方法和技巧。经过多年的实践,收到了良好的效果。
[1] 孙喆,尹晓红,卢世荣,等.理想流体伯努利方程在化工原理教学中的应用[J].化工高等教育,2012,(1):102~104.
[2] 邵友元.机械能守恒方程应用中的几个问题的讨论[J].广州化工,2010,37(1):164~165.
[3] 张丽.浅谈伯努利方程在流体力学中的应用[J].教育教学论坛,2016,(28):207~208.
[4] 王志祥,黄德春.制药化工原理(第三版)[M].北京:化学工业出版社,2014:2.
[5] 冯尚华,何国芳,赵仁高,等.化工原理的案例教学[J].化工高等教育,2010,(6):79~81.
[6] 潘鹤林,齐鸣斋,黄婕,等.少学时化工原理课程教学改革初探[J].化工高等教育,2012,(4):97~100.
[7] 陈敏恒,丛德濨,方图南,等.化工原理(上册,第三版)[M].北京:高等教育出版社,2013:13~14.
[8] 张斌.伯努利方程的扩展讨论[J].塔里木大学学报[J].2008,20(4): 32~33.
[9] 夏清,陈长贵.化工原理(上册,修订版)[M],天津:天津大学出版社,2010:33~35.
[10] 官叶斌.实际流体伯努利方程式教学的几点讨论[J].安庆师范学院学报(自然科学版),2012,18(2):122~123.
