对一道课本习题的深层次探究

江苏省太仓市第一中学 朱雯婷

对一道课本习题的深层次探究

江苏省太仓市第一中学 朱雯婷

数学课本是数学教学的重要依据与材料，我们的日常教学都围绕课本展开，中考试卷中的不少试题也都源于课本中的例题与习题，很多是对课本例题与习题的拓展和延伸。因此，教师不仅要研究教材教法，还要善于挖掘教材中例题与习题的深层价值，对这些重要的资源进行进一步探究。笔者对苏科版八年级上册第67页第10题进行了深入研究，下面做简要说明与整理。

一、从一道课本习题出发

1．习题探究，紧抓关键

原题：如图1，△ABC和△CDE都是等边三角形，且点A、C、E在一条直线上。AD与BE相等吗？证明你的结论。

解析：解题关键在于证明△ADC≌△BEC。由“△ABC和△CDE都是等边三角形”知，AC=BC，DC=EC，∠ACB=∠DCE，易得∠ACD=∠BCE，由此证明△ADC≌△BEC(SAS)。再由“全等三角形对应边相等”得到AD=BE。

点评：这是初中全等证明中的经典类型，常见的，还有将两个等边三角形置换成两个等腰直角三角形等。

2．层层深入，探究整理

图1

上题图中还有很多值得进一步研究的结论：

结论1：如图2，记AD、BE交点为点O，则有∠AOB=∠DOE=60°。

解析：由“对顶角相等”易证∠AOB=∠DOE，故本题的关键在于证明∠AOB =60°。

解法一：由上题知△ADC≌△BEC，则∠DAC=∠EBC，即∠CAO=∠CBO，∴∠AOB=180°-（∠ABO+∠BAO）= 180°-(60°+∠CBO+∠BAO)= 180°-（60°+∠CAO+∠BAO）= 180°-(60°+60°)= 60°。

解法二：由上题知△ADC≌△BEC，则∠ADC=∠BEC。由外角知∠AOB=∠OAE+∠OEA=∠OAE+∠ADC=∠DCE=60°。

解法三：记BC、AD交点为点F，易证△AFC∽△BFO，故∠FOB=∠FCA=60°。

点评：解法一运用“三角形内角和为180°”，解法二运用“三角形的一个外角等于与它不相邻的两个内角的和”。两种解法在本质上是一致的。不论是哪种解法，都用到了△ADC≌△BEC。

结论2：如图3，记BC、AD交点为点F，BE、CD交点为点G，则有AF=BG。

图2

解析：由△ADC≌△BEC知∠DAC=∠EBC；由∠BCA=∠DCE=60°知∠BCA=∠BCG=60°，又∵AC=BC，故△AFC≌△BGC(ASA)，∴AF=BG。

点评：同理，易得：△DCF≌△ECG，DF=EG ，FC=CG。

结论3：如图4，连接FG，则有△CF G是等边三角形。

图3

解析：由上题知△AFC≌△BGC，则CF=CG，故△CFG是等腰三角形。又∵∠BCG=60°，∴△CFG是等边三角形。

点评：由此可以发现，不论两个等边三角形的边长如何变化，都能形成一个新的等边三角形。

结论4： FG∥AE。

解析：由上题知△CFG是等边三角形，则∠FGC=60°，易证∠FGC=∠DCE，故FG∥AE。

点评：有FG∥AE，就能得出图中许多对相等的角与相似三角形，如∠OFG=∠OAE，∠OGF=∠OEA，△OFG∽△OAE等。

结论5：如图5，连接OC，则有OC平分∠AOE。

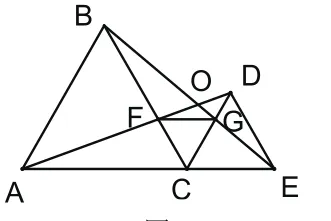
图4

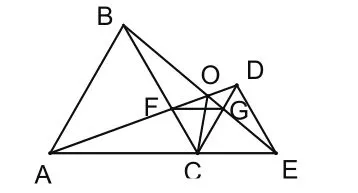
图5

解析：如图6，过点C作CP⊥AD，CQ⊥BE。

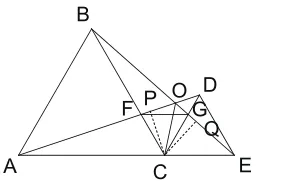
图6

解法一：由CP⊥AD，CQ⊥BE知∠APC=∠BGC=90°；之前已证明AC=BC，∠CAP=∠CBQ，故△CAP≌△CBQ，可得CP=CQ，又∵CP⊥AD，CQ⊥BE，则点C到∠AOE两边的距离相等，故点C在∠AOE的角平分线上，OC平分∠AOE。

解法二：CP是△ADC中AD边上的高，CQ是△BEC中BE边上的高，而△ADC≌△BEC，易证CP=CQ。由此，可证OC平分∠AOE。

点评：对比两种解法，显然解法二更简单。纵观前5个结论，每一个结论都直接或间接地用到了△ADC≌△BEC，这是本系列问题的根本所在。

结论6：图5中度数为60°的角共有13个。

解析：图5中的三个等边三角形中共有9个角的度数为60°。由结论1知∠AOB=∠DOE=60°，则∠AOE=120°，又∵ OC平分∠AOE，∴∠AOC=∠EOC=60°。故共有13个度数为60°的角。

点评：由以上分析可知，不论两个等边三角形的边长如何变化，都有∠AOC=∠EOC=60°。此系列问题含有多个“动中取静”的结论，可在几何画板中动态演示并度量，以增强感性认识。

解析：设 AC=x，FG=y，则 CD=CE=a-x，DG=CD-CG=CDFG= a-x-y。 由FG∥AE知，当时，y有最大值当两等边三角形边长相等时，线段FG有最大值

点评：本题采用方程与函数思想解决，用代数方法巧妙地解决了动点问题。

3．变化引申，拓展升华

拓展1：如图7，已知点C为线段AE上一个点，△ABC与△CDE都是等边三角形。

（1）求证：AD=BE；

（2）若把原题中“△ABC与△CDE

都是等边三角形”换成“四边形AFBC与四边形CDHE都是正方形”（如图8），此时AD与BE的数量关系如何？

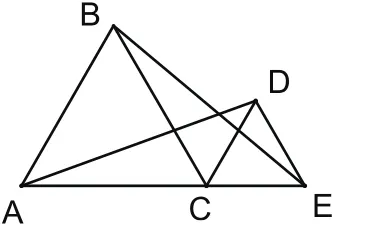
图7

图8

解析：不难证明△ADC≌△BEC，从而得AD=BE。

点评：本题第一问即为课本习题，第二问是从三角形到四边形的拓展与推广，更进一步可得：直线AD⊥直线BE。

拓展2： 如图9，△ABC与△CDE都是等边三角形，BE与AC交于点F，AD与CE交于点G，直线BE与直线AD交于点O，连接OC。

求证：（1）∠AOB=∠DOE=60°；

（2）OC平分∠BOD。

解析： 易证△BCE≌△ACD，模仿结论1的证明，即得∠AOB=∠DOE=60°；模仿结论5的证明，即得OC平分∠BOD。

点评：本题是原题的拓展，将“点A、C、E在一条直线上”这一特殊情况一般化。

拓展3：如图10，点A、C、E在同一直线上，点B、D在直线AE的同侧，BA=BC，EC=ED，∠ABC=∠CED，直线AD、BE相交于点O。

（1）若∠ABC=60°，则 ∠AOB=___________；

（2）若∠ABC=90°，则∠AOB=___________；

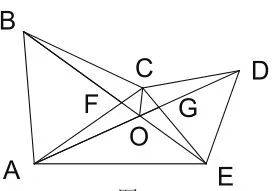
图9

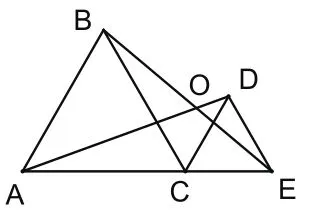
图10

解析：（1）即为结论1，易证△ADC≌△BEC。（2）易证△ADC∽△BEC，故∠AOB=∠OAC+∠OEC=∠OAC+∠ODC=∠DCE=45°。（3）与（2）证法相同，∠AOB=90°

点评：第一问就是结论1，第二问是第一问的变式，第三问是前两问的推广，要求学生“动中取静”展开研究。

二、让例题习题成为数学知识与方法生长的土壤

在升学压力巨大，各地齐抓教学质量的大背景下，我们都在尝试提高本门功课的教学质量。如何真正做到在不加重学生负担的前提下，提高教学质量？ 这应该成为每一位数学教师的追求。

以教材例题习题为依托进行变式教学，组织学生深层研究与拓展发散，是对教材再创造的一种形式，是提高学生数学素养的有效途径，同时也是提高单位时间内教学效率、减轻学生负担的一种行之有效的教学方法。