高速卷绕机传动轴的振动分析及控制研究

2018-01-11张君浩董学武王东强

中原工学院学报 2017年6期

张君浩，董学武，王东强

(中原工学院，郑州 450007)

传动轴是高速卷绕机传动系统的核心，是传递电机动力、保证卷绕机高速运转的关键部件，其性能直接影响卷绕机的工作状态[1-2]。卷绕机以1 500 r/min(25 Hz)旋转时会产生振动和噪声，合理设计其核心部件——传动轴，对减少卷绕机振动十分重要[3]。本文拟对传动轴模态分析研究，得到传动轴的振动特性参数，为进一步研究传动轴动平衡提供参考。

1 模态分析理论

模态分析是在振动力学基础上，通过模态参数研究结构动力特性的。模态分析的经典定义为：将线性定常系统振动微分方程组的物理坐标变换为模态坐标，使方程组解耦，成为一组以模态坐标及模态参数描述的独立方程，以便求出系统的模态参数。坐标变换的变换矩阵为模态矩阵，其每一列均为模态振型[4]。通常将模态分析分为理论模态分析和试验模态分析。理论模态分析通常是通过软件进行的，例如ANSYS有限元仿真分析。理论模态分析需要建模，设置与其运动状态一致的约束，并施加合理的载荷。但是，因实际构件的质量分布不匀，所以软件仿真易出现误差。试验模态分析是通过试验分析来研究构件模态参数的。由于人工操作、环境等因素会对试验造成误差，因此可将理论模态和试验模态相结合来研究构件的真实特性[5]。

传动轴的运动方程可以表示为黏性线性微分方程：

(1)

当P(t)=0时，忽略阻尼，可得到无阻尼自由振动的微分方程：

(2)

设特征解为：x=φejωt

(3)

式中：φ为自由响应的位移幅值矩阵；ω为自由响应的频率矩阵；j为复数的虚部。

将式(3)代入式(2)，可得如下方程:

(K-ω2M)φ=0

(4)

式(4)的特征方程为：|K-ω2M|=0

(5)

解特征方程(5)得：0<ω1<ω2<…，ωn。其中ωi(i=1,2,…,n)为振动系统第i阶的固有频率。

将ωi代入式(4)可得传动轴的固有振型：

φi=[φ1i,φ2i,…,φni]T(i=1,2,…,n)

(6)

2 有限元仿真模态分析

2.1 建立模型

利用Solidworks建立传动轴的三维几何模型，并对其进行简化处理，忽略传动轴的倒角、圆角(见图1)。

图1 传动轴几何模型

将建立的三维模型导入ANSYS Workbench软件中，设定传动轴材料属性。传动轴材料为40Mn，弹性模量为2.09×105MPa，泊松比为0.28，质量密度为7.87×103kg/m3。在ANSYS Workbench系统中使用Engineering Data中的Structural Steel命令，对传动轴模型进行参数设置；利用四面体单元自由划分网格技术对传动轴划分网格，形成的节点数为2 842，单元格为1 443个。有限元划分网格模型如图2所示。试验模态传动轴处于无约束状态，不添加载荷。为与传动轴试验模态对比，有限元仿真中传动轴也设置为自由约束，不添加任何约束。自由约束模态的阶数设置为12阶。

图2 有限元划分网格模型

2.2 自由模态仿真

在设置参数后，利用Mechanical软件求解，并点击Solution菜单命令下的Solve命令，对传动轴模型进行仿真，可得到传动轴自由约束的仿真模态频率(见图3)。

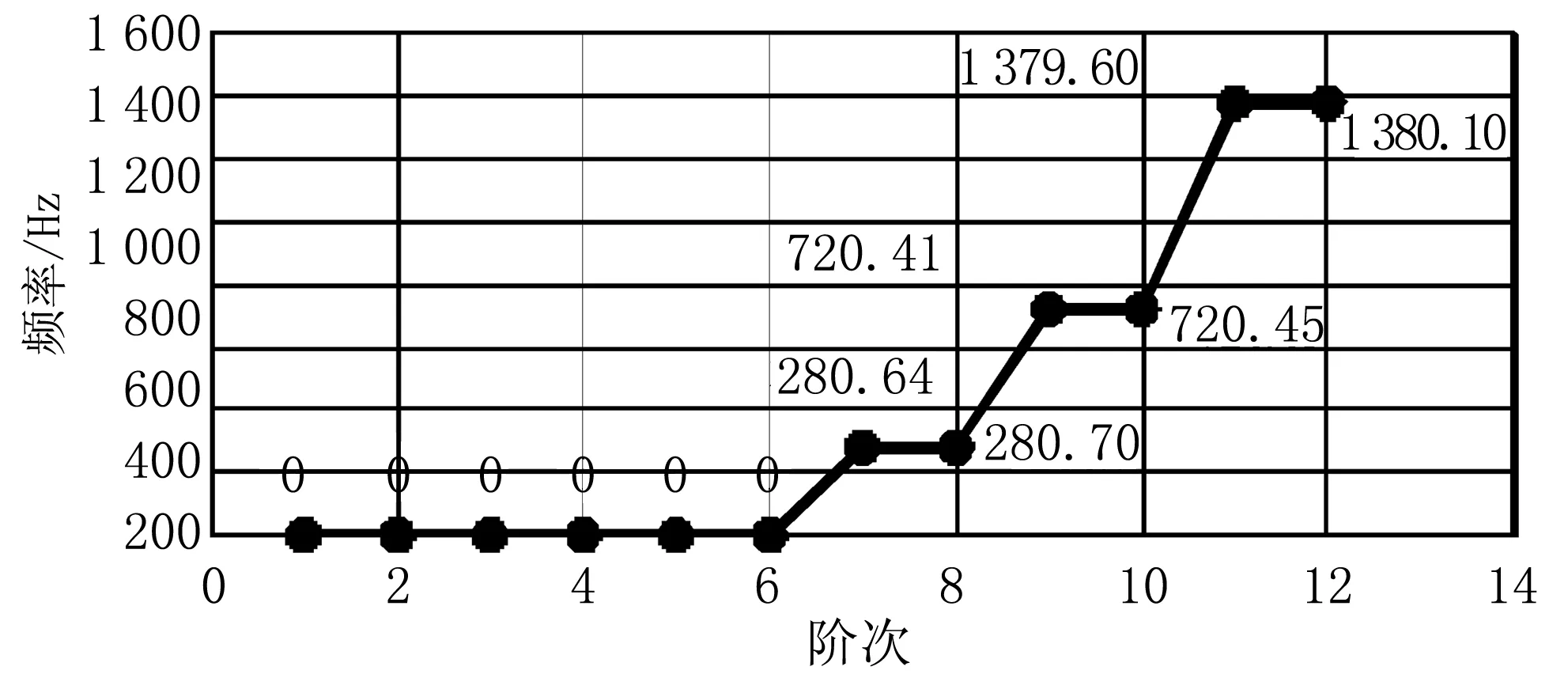
图3 传动轴自由约束的仿真模态结果

对传动轴进行自由模态分析，没有施加任何约束，前6阶模态频率为传动轴刚体模态。从仿真结果可以看出，前6阶模态频率都为0。这是由于这6阶模态分别为传动轴3个方向的转动及平动。其后续的4阶(第七阶、八阶、九阶和十阶)模态振型如图4所示。

图4 4阶(第七——十阶)自由模态振型

2.3 约束模态仿真

利用上述模型可进行约束模态分析。传动轴装配时右端与连体轴承结合件通过联轴器连接。为了与实际工作状态一致，对约束模态在ANSYS Workbench系统中传动轴安装联轴器部位(模型右端)施加圆柱面约束(Cylindrical support)，且约束模态的阶数设置为6阶。传动轴添加约束的仿真模态结果如图5所示。仿真得到的6阶模态振型如图6所示。

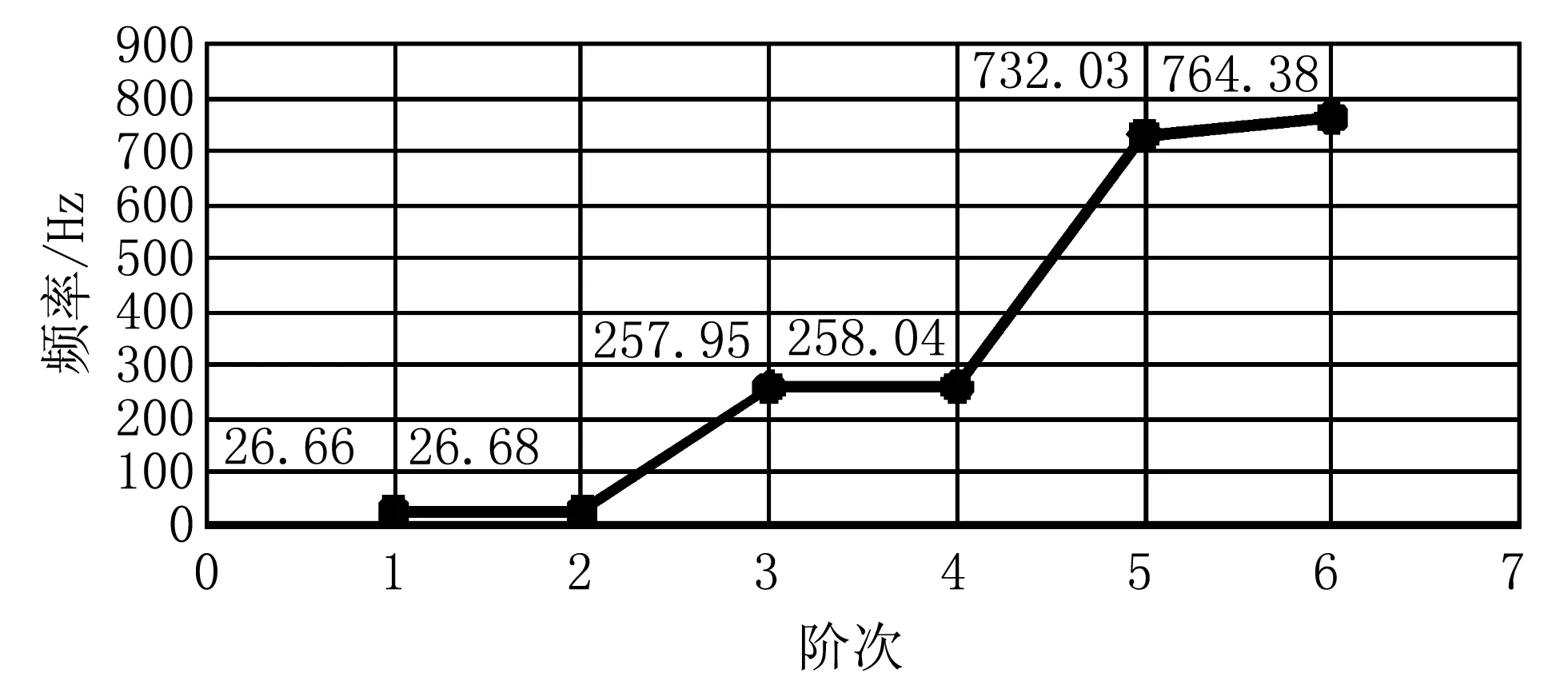
图5 传动轴添加约束的仿真模态结果

图6 6阶(第一——六阶)约束模态振型

3 试验模态分析

传动轴试验模态分析首先是对传动轴结构进行测试，然后分析测试结果，得到传动轴试验模态参数。使用的试验仪器包括：美国Data Physics(DP)公司信号分析系统，法国N-Modal模态分析系统、三项加速度传感器和力锤。

试验准备时使用橡胶垫支撑传动轴。其支撑方式为自由支撑。在进行传动轴测点布置时，因为传动轴的结构特殊，其横截面直径比长度小得多，所以可将传动轴简化为梁结构，通过分析对比，在传动轴上均匀分布11个测点。这样的测点布置使试验结果能够更好地反映传动轴的基本特征。将传动轴、三向加速度传感器、动态信号分析系统连接起来，并进行参数设置。根据传动轴实际情况，设定分析频率(1 600 Hz)、采样时间(4 s)、力信号、响应信号和平均次数(5次)，采用手动控制方式，在动态信号分析系统中激活三向加速度对应的通道。

模态试验采用锤击法。利用合适的力锤敲击传动轴测点，在脉冲力激励下，测量传功轴各测点的响应信号。利用力锤依次敲击传动轴的11个测点，通过三向加速度传感器拾取X、Y、Z3个方向的响应信号，使用美国DP公司的Signal Calc Mobilyzer Ⅱ动态信号分析仪进行信号采集，每个测点重复3次，排除其他噪声可能引起的误差，对3次测量结果取平均值，最后将其导入提前设置的N-Modal模态分析系统进行模态分析，得出传动轴的模态振型(见图7)。

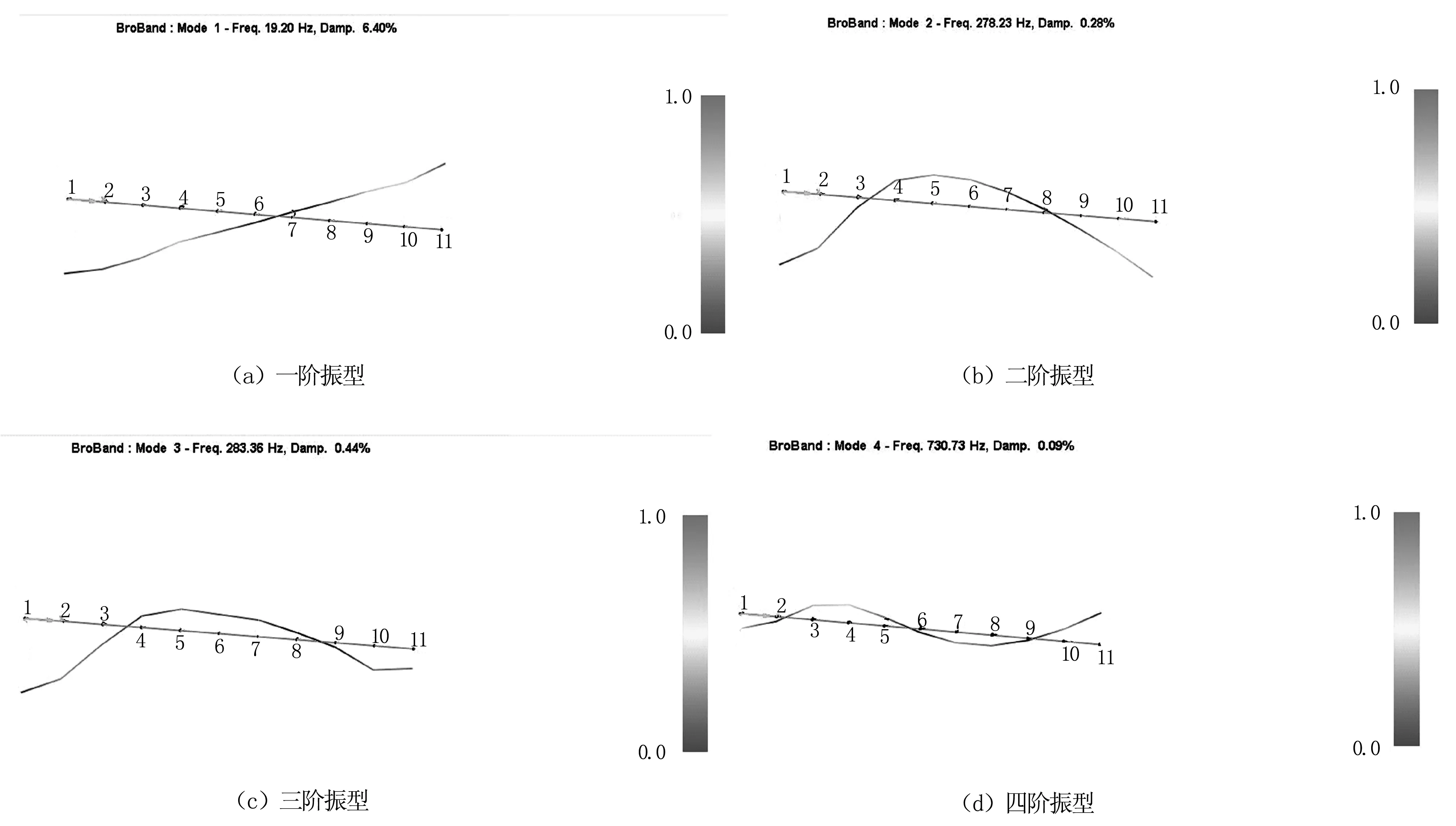
图7 传动轴试验模态振型

4 仿真与试验结果对比

在ANSYS Workbench自由约束仿真中得出固有频率和模态振型，并且，在建立传动轴模型时进行简化处理。一阶自由模态仿真未出现与试验模态相近值，属于合理现象。通过比较前6阶模态，除第一阶外，其他阶次自由模态仿真与试验模态的固有频率误差分别为-0.87%、0.94%、1.41%、2.43%、0.15%，误差在合理范围内，这验证了所建立模型的正确性(见表1)。