基于Hopfield神经网络的路径优化

欧阳玲

(中原工学院， 郑州 450007)

某公司决定派遣调查员调查市场行情，现有N个城市，要求调查员调查每一个城市，并且不能重复，最后返回公司所在城市。如何安排调查顺序，使其路程最短呢? 这正是旅行商问题(Traveling Salesman Problem，TSP)[1]研究的范畴。由于路径数目会随着城市数目的增加呈指数增长，当N很大时，用常规方法在庞大的搜索空间寻找最优解变得非常困难。本文基于Hopfield神经网络对旅行商问题进行研究，建立能量函数，提出设计方法，给出路径优化的解决算法，并对城市数目N分别为8、20、40的旅行路径进行计算机MATLAB模拟仿真。

1 Hopfield神经网络模型能量函数

Hopfield神经网络模型由许多互联的神经元组成，如图1所示。

对于一个神经元i，ui为其状态输入；R与Ci分别为输入电阻和输入电容；Ii为输入电流；wij为j神经元和i神经元之间的连接权值；vi为神经元的输出，是神经元状态变量ui的非线性函数。

对于Hopfield神经网络的第i个神经元，可采用微分方程建立其输入、输出关系[2]，即：

(1)

图1 Hopfield 人工神经网络模型

在状态空间中考虑Hopfield神经网络的动态特性，分别令U=(u1,u2,…,un)T为具有n个神经元的Hopfield神经网络的状态向量，V=(v1,v2,…,vn)T为输出向量，I=(I1,I2,…,In)T为网络的外加输入向量。为了描述Hopfield网络的动态稳定性，可定义标准能量函数为[2]：

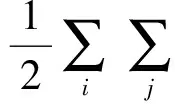
(2)

针对旅行商问题，将式(2)转化，以便与神经网络对应。这里，采用N阶换位矩阵表示调查者访问N个城市[1]。例如，当城市数目N=4时，集合表示为{A，B，C，D}，要求经过的路线是从城市D出发，中间依次经过城市C、B、A，最终返回城市D。若用矩阵来表示输出的有效解，“1”代表到达，“0”代表未到达，则有表1所示4个城市访问路线的二维矩阵。

表1 4个城市的访问路线

如果访问路线是一个有效的路径，矩阵中每一行每一列的元素是有规律的，即每行每列中“1”的个数为1，其余的都为0。如果不是这样的矩阵，则说明这个访问路线是无效的。对于一个神经元(x，i)，用Vxi表示这个神经元的输出，Uxi表示相应的输入。如果在i位置到达城市x，则神经元的输出为1，否则为0。

Hopfield定义了针对TSP问题的能量函数[3]：

(3)

式中：A、B、C和D是权值；dxy是城市x与城市y之间的距离。

在该能量函数中，E的第一项是行能量函数，第二项是列能量函数，第三项是全局约束函数，这3项是约束项，最后一项是优化目标项。

(1)行能量函数：每行只有一个1，其余元素都是 0，假设第x行满足这个条件，那么第x行的所有元素两两相乘再求和，结果应该是0。根据这个约束，可构建出能量函数中的第一项：

(4)

式中：A>0，是常数；当矩阵每一行1的个数不大于1时，E1达到最小，即E1min=0。

(2)列能量函数：每列只有一个1，其余元素都是 0，假设第x列满足这个条件，那么第x列的所有元素两两相乘再求和，结果应该是0。根据这个约束，可构建出能量函数中的第二项：

(5)

式中：B>0，是常数；当矩阵每一列1的个数不大于1时，E2达到最小，即E2min=0。

(3)全局约束函数即能量函数的第三项：

(6)

式中：C>0，为常数。全局约束表示当矩阵中1的个数恰好为N时，E3min=0。

(4)考虑路径最短的优化目标，可以构建出能量函数的第四项：

(7)

式中：D>0，为常数；dxy表示城市x到城市y的距离。从式(7)可以看出：若城市x和城市y在路径中相邻的话，Vy，i+1和Vy，i-1必定有一项为0，一项为1；若城市x和城市y在路径中不相邻的话，Vy，i+1和Vy，i-1全为0。通过式(7)可以计算出路径的长度。

由式(4)-式(7)可以构成用Hopfield网络求解TSP问题的能量函数式(3)。

2 采用Hopfield网络求解TSP问题的算法

表2 城市数与路径数

当N比较大时，很难求取精确解。若直接采用能量函数式(3)进行求解，则可能存在局部极小值的问题。为此，可将式(3)优化为[4]：

(8)

由式(2)和式(8)，分别对时间t微分，可得如下动态方程：

(9)

采用MATLAB进行计算机模拟，具体步骤如下：

(1)令网络的初始值t=0，设置相关参数A、D、μ的值；

(2)计算N个城市之间的距离dxy(x,y=1,2,…,N)；

(3)设置神经网络输入Uxi(t)的初始值；

(5)根据一阶欧拉法，求解

(10)

(6)采用Sigmoid函数计算Vxi(t)，满足上述行、列能量函数及全局约束最小的条件(即矩阵每一行只有一个1，每一列也只有一个1，其余都为0)，即：

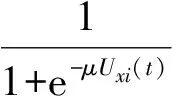
(11)

式中，μ>0，μ的大小决定了Sigmoid函数的形状；

(7)根据式(8)计算能量函数E；

(8)若路径合法或迭代结束，则终止仿真，否则返回步骤(4)；

(9)输出原始路径及最终的优化路径，以及能量函数随迭代次数变化的曲线[5]。

3 仿真实例

首先需要设置实验中用到的网络参数，并令式(8)中A=1.5，B=1.5，D=1.0；取式(10)中ΔT=0.01，Uxi(t)初始值在±0.001之间；在式(11)中，只有取较大的μ值(μ=50)，才能保证稳态时Vxi(t)趋向于1或者0。

路径矩阵中的元素是对应于实验结果的。在程序运行后，如果仿真成功，即寻优路径有效，矩阵中的每一行只有一个1，每一列也只有一个1，即代表每个城市只去一次；若寻优路径无效，则需要重新进行优化实验。

然后，在仿真中对N分别为8、20、40的旅行路径进行优化(见图2-图7，表3-表5)[6]。

注：(X,Y)为坐标。图2 初始路径及优化后的路径(N=8)

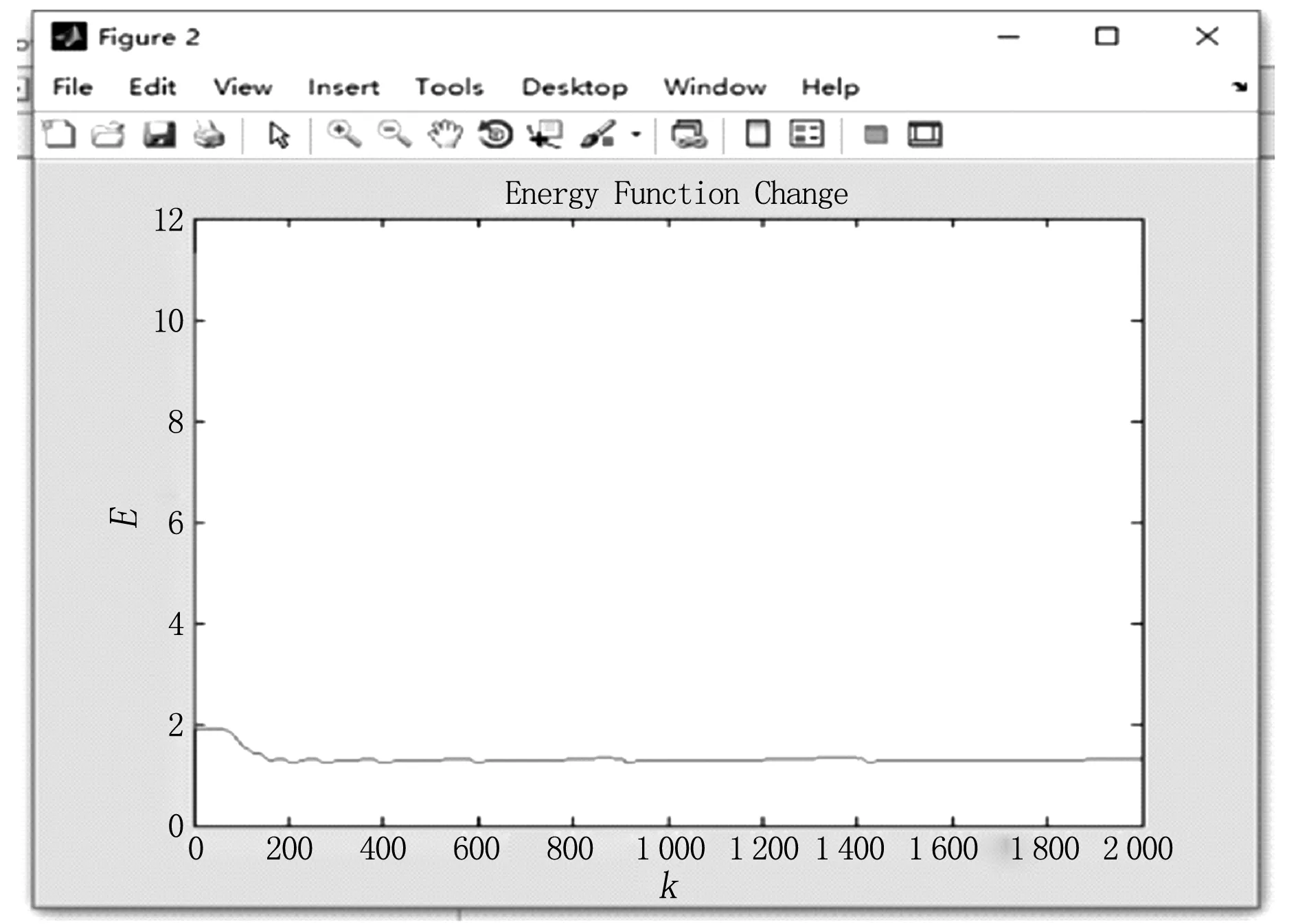
注：E为能量函数；k为迭代次数。图3 能量函数随迭代次数的变化(N=8)

注：(X,Y)为坐标。图4 初始路径及优化后的路径(N=20)

注：E为能量函数；k为迭代次数。图5 能量函数随迭代次数的变化(N=20)

注：(X,Y)为坐标。图6 初始路径及优化后的路径(N=40)

注：E为能量函数；k为迭代次数。图7 能量函数随迭代次数的变化(N=40)

表3 各城市坐标(N=8)

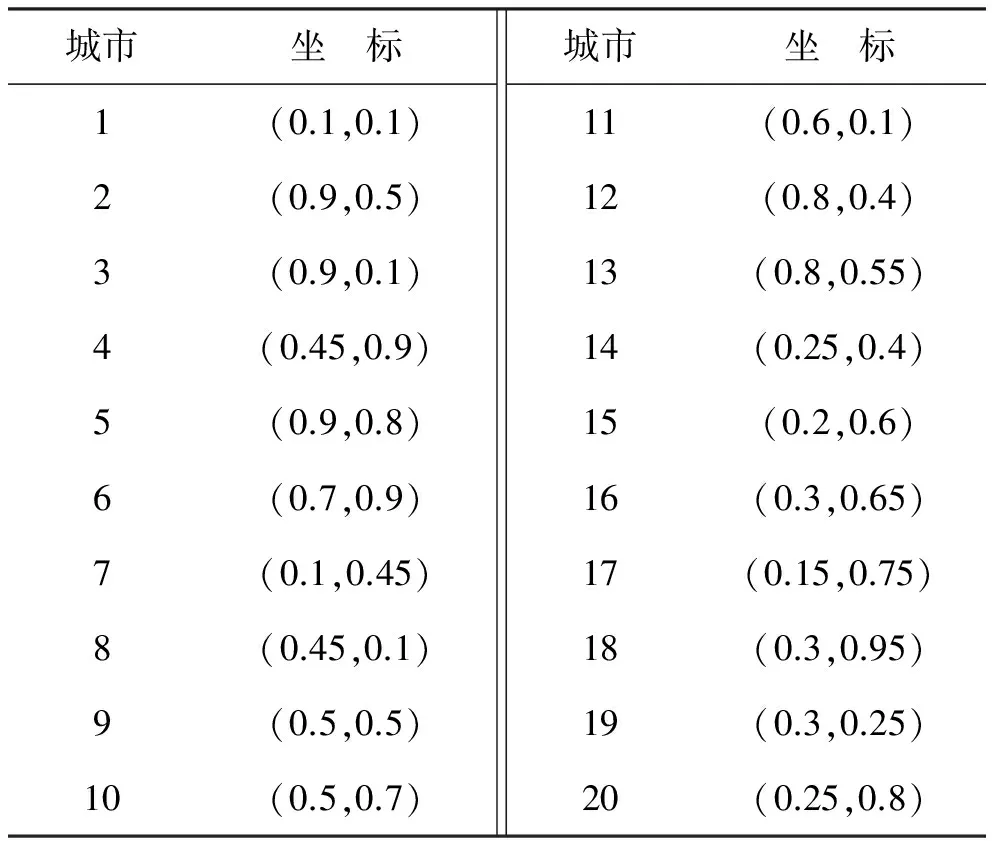
表4 各城市坐标(N=20)

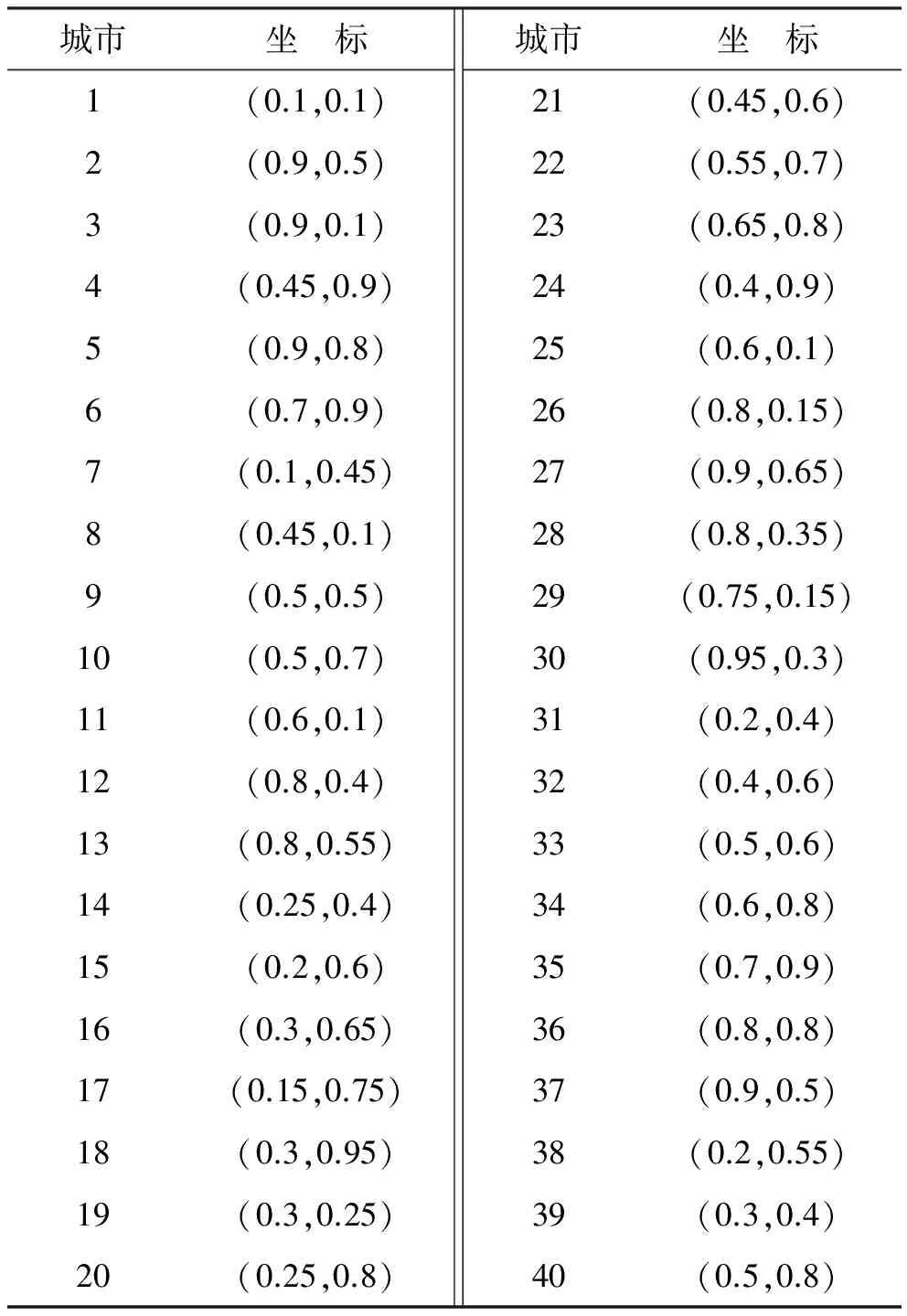
表5 各城市坐标(N=40)

上述仿真实验，在100次中，基本上有90次以上可收敛到最优解，表明算法有稳定性。以N=8为例，最后的仿真结果如图2和图3所示。在图2中，左边为初始路径(Original Route)，右边为优化后路径(New Route)。可明显看出，优化后相互交叉的路径大大减少，路径规划更为合理。图3显示的是能量函数随迭代次数的变化情况。可以看出，E的值随着迭代次数的增大而减小。N=20及N=40时，结论相似。

对N=8、20、40时进行的计算机MATLAB仿真表明，最终能量函数都是最小的，即收敛到了极小点。这与仿真之前的原理分析是一致的，路径优化的原理与研究方法是正确的。实验证明，无论是Hopfield网络的设计还是算法都是有效的，而且实用价值很高。

4 结 语

本文在分析Hopfield神经网络和TSP算法的基础上，进行了求解TSP问题的Hopfield网络设计，并采用MATLAB针对不同城市数N的路径优化问题进行了仿真，获得了经典组合优化问题的最优解，验证了算法的有效性。针对标准TSP能量函数易引入局部极小值的问题，后续将展开深入研究，进一步优化能量函数,以提高在N值更大时TSP最优解收敛的成功率。

[1] 吴高航.Hopfield神经网络解TSP问题及能量函数参数分析[J].现代计算机，2016(9)：90-92.

[2] 刘金琨.智能控制(第三版)[M].北京：电子工业出版社，2014：167-172.

[3] Hopfield J，Tank D W. Neural Computation of Decision in Decision in Optimization Problems[J]. Biological Cybernetics，1985,52：141-152.

[4] 孙守宇，郑君里.Hopfield网络求解TSP的一种改进算法和理论证明[J].电子学报，1995，23(1)：73-78.

[5] 张丽霞，赵又群，潘福全. Hopfield神经网络算法求解路网最优路径[J].哈尔滨工业大学学报，2009,41(9)：222-224.

[6] 闻新，李新，张兴旺,等.应用MATLAB实现神经网络[M].北京：国防工业出版社,2015:202-247.