弦支穹顶结构中预应力设计的方法

(广州大学土木工程学院 广东 广州 510006)

弦支穹顶结构中预应力设计的方法

陈建亮

(广州大学土木工程学院广东广州510006)

弦支穹顶结构最起初是由日本川口卫学者将索穹顶、单层网壳组合，从而提出了一个新型的弦支穹顶结构体系。之后的弦支穹顶为什么可以成为高性能的空间结构体系是由于它的高强度拉索和预应力的引入。所以，预应力如何设计就成了弦支穹顶结构设计的主要问题。预应力的施加主要是在环索中，施加预应力不能过大也不能过小，否则会影响整个结构的强度和用钢量的经济问题。本文作者详细介绍了弦支穹顶中最常用的环索预应力比的确定方法-几何法。

弦支穹顶；环索；预应力

一、引言

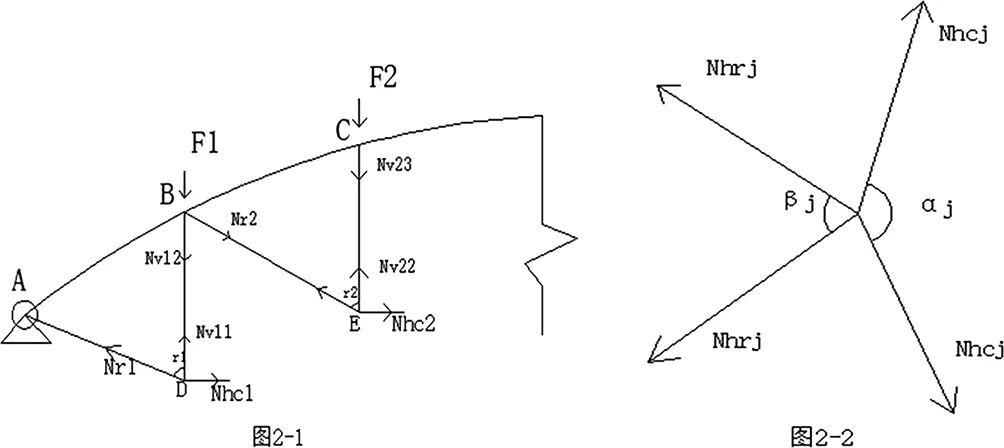
目前，研究环索预应力比的方法有很多种，但最常用的有一种方法我们称其为几何法，这种方法概念清晰简单，便于理解，容易接受，这种方法主要适用于联方型和肋环型等比较小的跨度的圆形弦支穹顶。这里以联方型弦支穹顶为例来设计其预应力。弦支穹顶的平面图如下。这里预应力的引入主要是将屋面荷载转化为节点荷载，然后力从上面一层层往下传，这里要达到的理想状态最优的效果是结构预应力+结构自重+1.0恒载+0.5活载共同作用下支座的径向反力为零。

二、预应力的确定方法

(一)基本原理

这里首先考虑理想状态下结构的预应力设计，即将结构设为对称的，每环预应力大小假设相同，以荷载产生的等效节点力与撑杆竖直向上的力为平衡原则。这里以联方-凯威特型弦支穹顶为例，所以这里环索处的节点是连接两径向撑杆和两个环向拉索和一根竖向撑杆。这里图2-1为弦支穹顶平面图，图2-2为中间某节点在水平面上的投影，其中竖向撑杆即垂直与平面，仅有两个环向拉索跟径向拉索，这里的Nhrj是Nrj在水平面的投影。

(二)内力推导

这里由图2-2可明显的得出

(1)

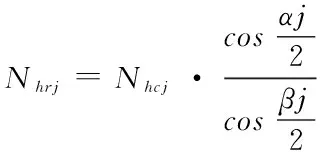
(2)

这里假设BCE为最内环弦支穹顶，则可由C,E节点的力的平衡关系可得出：

在竖直方向投影得Nr2·cosr2=F2

(3)

在水平方向投影得Nr2·sinr2=Nhr2

(4)

由此可得竖杆的轴力如下，其中数字2是因为有两个径向拉索

(5)

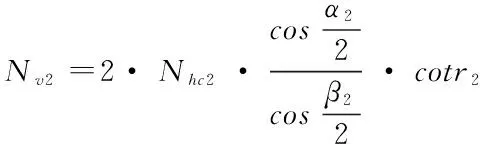
(6)

这里的公式(6)即为竖向撑杆与环向拉索的关系。下面来导出环索预应力与等效节点力的关系。因为之前假设BCE为最内环，所以在C节点处有公式：

(7)

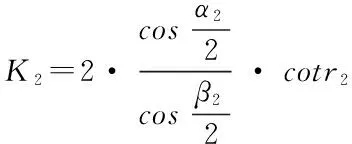
(8)

所以可得出F2=Nhc2·K2

(9)

之后便可得出等效节点了与环索预应力的关系，即

(10)

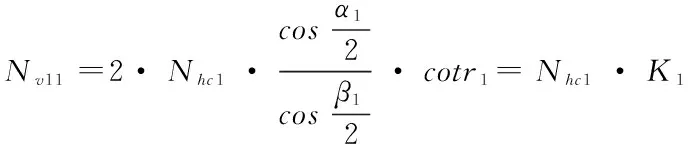
(11)

这里在竖直方向投影便可得到

(12)

所以最终得到Nv12=F1+F2

(13)

再由节点平衡关系可得F1+Nhc2·K2=Nhc1·K1

(14)

这就得到了预应力为Nhc1=(F1+Nhc2·K2)/K1

(15)

所以n环的弦支穹顶就可由上面的公式得到：

Nhcj=(Fj+Kj+1·Nhc(j+1))/Kjj=n-1，n-2，…，1

其中Fi——第i环环索的等效节点力

Nri——第i环径向拉索的合力

Nhci——第i环环向拉索的轴力

Nvij——第j环索力引起的第i环的撑杆轴力

Nhri——Nri在水平面的投影分力

几何法的概念清晰，逻辑性便于理解，在实际应用过程中具有广泛的应用。但是，几何法也有一定的弊端，因为这种方法假设条件太多，计算量又较大，而且，弦支穹顶的各个角度都是按对称的原则推理的，当在实际过程中结构往往不可能是完全对称的会带来一定的误差。

[1]李禄.基于张拉整体理论的弦支守顶结构的理论和试验分析.天津大学硕士研究生毕业论文，2000.4

[2]陈志华，李阳，康文江.联方型弦支穹顶研究[J].土木工程学报，2005，38(5)：34-40.

陈建亮(1991-)，男，汉族，河北沧州市人，学生，工学硕士，广州大学，建筑与土木工程钢结构方向。