认知雷达波形自适应数据关联跟踪算法

王树亮，毕大平,2，阮怀林

(1. 国防科技大学电子对抗学院，合肥 230037；2. 安徽省电子制约技术重点实验室，合肥 230037)

认知雷达波形自适应数据关联跟踪算法

王树亮1，毕大平1,2，阮怀林1

(1. 国防科技大学电子对抗学院，合肥 230037；2. 安徽省电子制约技术重点实验室，合肥 230037)

针对杂波背景下多交叉机动目标跟踪问题，提出一种认知雷达波形自适应数据关联跟踪算法，该算法选取目标距离-速度-方位作为观测量，并通过调整波形参数来动态改变量测误差协方差。首先，基于信息融合思想提出一种优化的概率数据关联(OPDA)算法，算法充分融合目标位置特征和运动特征对多目标交叉区域公共量测进行分类，使多交叉机动目标跟踪问题转化为多个单机动目标跟踪问题。然后，对实时更新的目标航迹，采用修正的Riccati方程估计下一时刻滤波协方差，并根据波形选择准则函数自适应选择下一时刻波形以提高系统跟踪性能。仿真结果表明，该算法增强了概率数据关联(PDA)算法的环境适应性，而且相比未采用波形自适应的数据关联算法有明显的优势。

认知雷达；优化概率数据关联(OPDA)；机动目标跟踪；波形自适应

0 引 言

杂波环境下的数据关联问题一直是多目标跟踪领域的难点问题，目前主要有两种解决途径[1]，一类是基于随机有限集的方法[2-3]，避免了目标与量测之间的数据关联计算，但过程中涉及到复杂的集合积分运算，在实际中难以求解，在降低计算量的同时保证目标跟踪精度还需不断深入研究完善。另一类方法是先关联后跟踪[4]，最常见的是最近邻数据关联算法和全邻数据关联算法，最近邻算法结构简单，但仅能跟踪稀疏杂波背景中的单个目标；概率数据关联(PDA)和联合概率数据关联(JPDA)算法是典型的全邻数据关联算法，PDA算法容易实现，但局限于目标的关联门不相交或没有回波处于相交区域的环境；JPDA算法是目前公认的在密集杂波多目标环境下，跟踪效果最理想的数据关联算法之一，但当目标数目和有效量测数增大时，可行性联合事件数目呈指数增长，导致算法的计算量也呈指数增长甚至出现组合爆炸现象，工程上不易实现。

认知雷达[5]由于具有良好的环境认知属性，被认为是下一代雷达的发展方向。认知跟踪雷达相比于传统跟踪雷达有下面三个鲜明的特点[6]：1)接收端，在与环境交互中，通过反复学习获得经验；2)发射端，以一种最优化的方式来自适应地发射与接收端相匹配的信号；3)反馈，协调接收和发射两端，使其保持同步调整。自适应波形选择技术就是通过智能地选择合适的发射波形使得接收端获得良好的数据以提高系统跟踪性能。Kershaw和 Evans[7-8]利用在原点处雷达波形模糊函数的 Fisher信息矩阵，得到了量测误差和波形参数的关系，并结合PDA算法研究了杂波背景下波形脉宽参数选择问题，使雷达目标跟踪发射端信号和接收端数据处理联系在了一起。文献[9,10]研究了杂波背景下多个目标跟踪问题，通过动态选择4种调制波形来减小量测误差协方差，并采用粒子滤波算法来处理非线性量测问题。文献[11]基于修正的PDA算法研究了杂波背景下单个目标波形自适应跟踪问题。以上研究虽然取得一定效果，然而都是基于距离-速度作为量测信息，文献[12]认为目标跟踪的精度与方位的量测精度有着密切的联系，尤其当目标相对雷达较远时，角度误差对跟踪精度影响较大，并针对二维空间的距离、速度和方位量测，建立了3个变量的误差克拉美罗下限方程，然而文献并没有对杂波背景下目标跟踪问题进行深入探讨。

在以上文献研究的基础上，本文重点就杂波背景下交叉机动目标跟踪问题进行研究，主要创新点有两个方面：1)数据关联算法方面，如果被跟踪的多个目标的相关波门不相交，或者没有回波落入波门的相交区域，此时多目标数据关联问题可简化为多个单目标数据关联问题，可以利用传统的PDA算法求解[4]，此外可以利用目标更多的属性特征对数据关联算法进行改进[13]，基于以上思想，提出一种融合位置特征和目标运动特征的OPDA算法，算法对关联门交叉区域公共量测进行分类，使其归属于某个特定的关联门内，从而将多交叉机动目标跟踪问题转化为多个单机动目标跟踪问题；2)基于认知的思想，将自适应波形选择与数据关联算法相结合，构建目标距离、速度和方位3个变量的误差克拉美罗下限方程，并根据波形选择准则函数动态调整波形参数，使系统总体跟踪性能得到较大幅度的提高。

1 跟踪模型

1.1 发射信号模型

假设一个窄带发射脉冲信号[7]

(1)

单个目标的接收信号可表示为

(2)

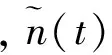
1.2 数据处理模型

1.2.1线性状态模型

目标运动的离散状态方程表示为

X(k)=Φ(k|k-1)X(k-1)+

(3)

对于非合作目标，其运动状态往往是未知的，利用“当前”统计模型自适应滤波算法[14]，它的基本思想是，若目标正以某一加速度机动时，它在下一瞬时的加速度取值范围是有限的，而且只能在“当前”加速度邻域内。算法通过对动态噪声方差自适应调整实现对机动目标的跟踪，相应的参数设置参见文献[14]。

1.2.2非线性量测模型

目标的量测方程为

Y(k)=h(X(k))+Vφ(k)

(4)

(5)

量测噪声Vφ(k)是零均值高斯白噪声，其协方差阵为Rθ(k)，波形φ有关[7]，{θ1,…,θk,…}∈φ为波形参数的可选集合，θk为k时刻选择发射的波形参数(如信号持续时间，调频率等)。接收机对目标的时延、多普勒和方位进行估计，估计值通过转换方程转化为目标的距离、速度和方位信息，相关参数见2.2节。

图1给出了基于认知雷达的波形自适应目标跟踪框图，接收机通过k-1时刻波形所产生的量测误差协方差Rθ(k-1)进行滤波，按照一定的准则，在波形库中选择合适的波形φ，用于下一时刻目标跟踪。

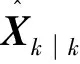
(6)

2 基于OPDA的波形自适应跟踪算法

2.1 OPDA算法

传统的PDA算法，主要利用了目标的位置信息，在处理杂波背景下单个目标跟踪问题时取得了较好的效果，然而算法不适于对多个目标特别是如图2所示在两个目标关联门交叉区域有公共量测的目标跟踪问题。

本文提出的OPDA算法的基本思路是基于信息融合的思想综合考虑目标位置特征和运动特征，计算交叉区域公共量测隶属于不同目标的程度，从而判断其目标归属。

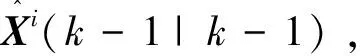
(7)

若目标在第k时刻的距离、方位新息方差为S(k)，

此时第g个有效回波量测隶属于目标i的隶属度为

(8)

b.运动特征基本思想是目标运动方向在短时

(9)

回波量测属于目标i的隶属度为

(10)

2.2 波形自适应概率数据关联算法

2.2.1滤波协方差

滤波协方差的一般表达式为[4]

Pkk(θk)=Pkk-1-(1-εk,0)Kk(θk)×

(11)

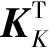
(12)

(13)

推导出滤波协方差的简化形式

Pkk(θk)≅Pkk-1-q2(ρVk(θk),PD)×

(14)

式(12)至(14)中，Yk-1为k-1时刻以前的量测集，q1,q2为尺度因子，ρ为杂波密度(每单位体积内的虚假量测数，本文中单位取每平方千米)，Vk(θk)为跟踪关联门体积，PD为检测概率，PG为门概率，当量测维数为3，关联门限取4个sigma点时，q2(ρVk(θk),PD)的实验近似表示式为[15-16]

q2(ρVk(θk),Pd)≈

(15)

2.2.2波形结构与量测误差协方差

Rθ(k)与发射波形参数有关，可以采用量测噪声协方差参数估计的克拉罗界表示，取发射信号为高斯包络线性调频信号形式即[7]

(16)

式中，λ为信号的有效持续时间；b为频率调制率；文献[3]指出信号模糊函数AF(τ,v)是信号时延多普勒频移(τ,v)的似然估计，其信息矩阵的逆J-1是参数估计精度的克拉美罗下界，其中

(17)

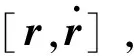
(18)

(19)

进一步考虑角度β测量误差协方差，其表达式为[17]

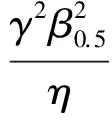
(20)

其中，β0.5为半功率波束宽度，γ与有效孔径宽度有关，是由孔径照射决定的，不同的照射方式其测量误差不同。综合式(19)、(20)，距离-速度-方位的测量误差协方差为

(21)

从(19)式中容易看出，当信号有效持续时间λ减小时，测距精度较高，而测速精度可能会随之降低；信号脉宽Ts=7.4338λ，若雷达带宽限定为B，则信号调频率b=B/Ts=B/(7.4338λ)，随着信号有效持续时间λ反比变化。波形自适应选择就是根据环境和目标机动情况动态调整脉冲有效持续时间从而使测距、测速精度达到某种平衡，提高系统总体性能。

基于OPDA的波形自适应机动目标跟踪算法流程框图如图5所示，该方法不仅能够解决机动交叉目标的跟踪问题，而且能够实时调整发射波形，从而提高系统总体跟踪性能。

3 仿真校验

假定使用的雷达能够测量目标的距离-速度-方位信息。进行M次Monte Carlo仿真实验，算法性能评价指标选取：a.距离、速度跟踪均方根误差；b.目标跟踪失败率，若第L(L≤M)次跟踪时某采样时刻距离估计偏离真实位置大于或等于3σr(其中σr是雷达传感器的距离测量误差标准差),就认为第L次跟踪失败。

目标运动轨迹

目标1初始位置位于(1.25×104,1.5×104) m，初始速度(-100,-50) m/s，目标在前17 s做匀速直线运动，从第18～43 s做角速度ω=4.77°/s的匀角速度左转弯运动，第44～53 s继续做匀速直线运动，第54～80 s做角速度ω=4.77°/s的匀角速度右转弯运动，从第81～100 s再做匀速直线运动。目标2初始位置位于(1.0×104,1.5×104) m，初始速度(100,-50) m/s，目标在前17 s做匀速直线运动，从第18～43 s做角速度ω=4.77°/s的匀角速度右转弯运动，第44～53 s继续做匀速直线运动，第54～80 s做角速度ω=4.77°/s的匀角速度左转弯运动，从第81～100 s再做匀速直线运动。图6为目标的运动轨迹，图7描述了当杂波密度为ρ=0.1时的目标观测及杂波分布情况。

假设雷达发射波形为X波段，载频为10.4 GHz，发射信号采用式(16)所描述的波形。雷达位于直角坐标原点，采用自适应跟踪方式，波形库内脉冲有效持续时间λ选择范围为[2×10-6,20×10-6]s，间隔为2×10-6s；调频斜率b设为0；天线为矩形孔径均匀照射，半功率波束宽度设为β0.5=3°。共有10种可选波形，各波形具有相同的能量，但由于脉宽不同其测速和测距精度不同。在距离r处雷达信噪比设为η=(r0/r)4,r0假设为50 km。

3.1 PDA算法、OPDA算法和JPDA算法比较

假定脉冲持续时间为λ2=4×10-6s，检测概率为1，表1给出了三种算法在不同杂波密度背景下，500次跟踪中的失败跟踪次数，表2给出了三种算法跟踪耗时。

表1 三种算法的目标跟踪失败次数Table 1 Number of losing tracking with three algorithms

表2 三种算法的目标跟踪耗时Table 2 Time consuming of tracking with three algorithms

3.2 WSOPDA和OPDA算法比较

对比本文基于波形选择的OPDA(WSOPDA)算法和未进行波形自适应的OPDA算法。对比算法中OPDA算法的波形持续时间分别选取为λ1=2×10-6s、λ2=4×10-6s、λ3=10×10-6s、λ4=16×10-6s和λ5=20×10-6s。

a) 表3给出了在杂波密度为ρ=0.1时，不同持续时间OPDA算法在500次跟踪中的跟踪失败数，其中WSOPDA算法的跟踪失败次数为7。

表3 不同波形OPDA算法对目标的跟踪失败次数Table 3 Number of losing tracking with different waveform OPDA algorithms

b) 图8、9给出了WSOPDA算法与λ2=4×10-6s的OPDA算法在跟踪不丢失情况下的距离、速度跟踪误差。图10给出了两个目标的实时动态波形选择情况。

仿真分析

①传统的PDA算法将跟踪关联门内的所有量测都认为是可能来自目标，根据全概率公式，通过计算各个点迹权值来估计目标的状态，对杂波密度下单个目标跟踪性能较好，但在多目标交叉跟踪中，全概率公式应用的前提难以保证，所以会出现跟踪偏离实际轨迹的现象。表1可知，当杂波密度增大为ρ=1时，其跟踪失败率高达20%以上。JPDA算法引入确认矩阵来表示有效回波和各目标关联门间的关系，是一种较优的算法，但其计算量较大，如表2所示，当杂波密度增大为ρ=1时，其计算耗时分别是PDA算法和OPDA算法的5倍和4倍。本文提出的OPDA算法由于对交叉门内公共量测进行了分类处理，从而将多交叉目标跟踪问题转化为多个单目标跟踪问题，其对杂波环境的适应能力相比PDA算法较为突出，时间性能上也明显优于JPDA算法，可以认为是PDA算法和JPDA算法的折衷选择。

②认知雷达应用于跟踪的特点就是能够自适应地根据环境和目标运动状态的改变调整波形参数，从表3可以看出，在杂波密度为ρ=1时，WSOPDA算法的跟踪失败率为1.4%，远低于采取固定波形的OPDA算法，反映出算法具有较强的环境适应能力和鲁棒性。

③由图8、9可以看出WSOPDA算法的目标跟踪精度要明显优于固定波形OPDA算法，仿真计算若采取固定波形λ1=4×10-6的OPDA算法，其对目标的距离和速度估计误差平均为73.37 m和29.45 m/s；而采用WSOPDA算法其对目标距离和速度的估计误差平均为55.49 m和24.11 m/s，估计精度分别提高24.4%和17.1%。这可以从图10波形适时选择中得到合理的解释，当目标处于转弯机动(第18～43 s和54～80 s)时，其距离变化较为明显，此时波形选择较小脉冲持续时间，保持较高的距离跟踪精度；当目标处于匀速运动(第1～17s、44～53 s和81～100 s)时，脉冲持续时间在最小值和最大值之间交替选择，动态平衡距离和速度误差，使系统总体跟踪性能得到持续稳定地改善。

4 结 论

本文提出一种基于认知雷达波形自适应的数据关联跟踪算法，主要的创新点有两个方面，一是对传统PDA算法进行了改进，得到一种优化的概率数据关联算法，将多目标交叉跟踪问题转化为多个单目标跟踪问题，增强了传统PDA算法的环境适应性，算法本质上是传统PDA算法和JPDA算法的折衷选择；二是基于认知的思想，把距离-速度-方位三个量测综合考虑，构建了信号端与数据处理端的联系，通过在每个时刻动态调整波形参数提高跟踪性能。限于篇幅，本文主要研究了单脉冲波形参数对跟踪的影响，接下来将对多组合脉冲参数对多目标跟踪影响及自适应选择问题进行深入探讨。

[1] 刘俊, 刘瑜, 何友, 等. 杂波环境下基于全邻模糊聚类的联合概率数据互联算法[J].电子与信息学报, 2016, 38(6): 1438-1445. [Liu Jun, Liu Yu, He You, et al. Joint probability data association algorithm based on all-neighbor fuzzy clustering in clutter [J]. Journal of Electronic & Information Technology, 2016, 38(6): 1438-1445.]

[2] Mahler R. Multi-target Bayes filtering via first order multi-target moments[J]. IEEE Transactions on Aerospace and Electronic System, 2003,39(4):1152-1178.

[3] 何友, 田淑荣, 孙校书. 一种基于随机集的模糊观测的多目标跟踪算法[J]. 宇航学报, 2008, 29(6):2007-2011. [He You, Tian Shu-rong, Sun Xiao-shu. Random sets-based multi-target tracking with ambiguous measurements [J]. Journal of Astronautics, 2008, 29(6):2007-2011.]

[4] 何友, 修建娟, 张晶炜. 雷达数据处理及应用(第二版)[M]. 北京：电子工业出版社, 2009:120-147.

[5] Haykin S. Cognitive radar: a way of the future[J], IEEE Signal Processing Magazine, 2006, 23(1):30-40.

[6] Haykin S, Zia A, Arasaratnam I, et al. Cognitive tracking radar[C]. IEEE Radar Conference, Washington DC, USA, May 10-14, 2010.

[7] Kershaw D J, Evans R J．Optimal waveform selection for tracking systems [J]. IEEE Transactions on Information Theory, 1994, 40(5): 1536-1550.

[8] Kershaw D J, Evans R J．Waveform selective probabilistic data association [J]. IEEE Transactions on Aerospace and Electronic Systems, 1997, 33(4): 1180-1188.

[9] Sira S P, Papandreou S A, Morrell D, et al.Waveform-agile sensing for tracking multiple targets in clutter [C].IEEE Information Sciences and Systems Conference, Princeton, USA, March 22-24, 2006.

[10] Sira S P, Papandreou S A, Morrell D．Dynamic configuration of time-varying waveforms for agile sensing and tracking in clutter [J]. IEEE Transactions on Signal Processing, 2007, 55(7): 3207-3217.

[11] 王宏强, 夏洪恩, 程永强, 等.基于MPDA的波形自适应目标跟踪[J].系统工程与电子技术, 2011, 33(11): 2389-2392. [Wang Hong-qiang, Xia Hong-en, Cheng Yong-qiang, et al. Adaptive waveform selection for target tracking based on MPDA[J]. Systems Engineering and Electronics, 2011, 33(11): 2389-2392.]

[12] 盛丹, 王国宏, 张翔宇. 基于波形捷变的多传感器机动目标跟踪[J].系统工程与电子技术, 2015, 37(3): 485-491. [Sheng Dan, Wang Guo-hong, Zhang Xiang-yu. Maneuvering target tracking based on waveform agility with multi-sensor [J]. Systems Engineering and Electronics, 2015, 37(3): 485-491.]

[13] 王树亮, 阮怀林. 基于模糊信息融合的快速数据关联算法[J]. 弹箭与制导学报, 2011, 31(1):201-203. [Wang Shu-liang, Ruan Huai-lin. Fast algorithm for data association based on fuzzy information fusion [J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2011, 31(1):201-203.]

[14] 周宏仁, 敬忠良, 王培德. 机动目标跟踪[M]. 北京：国防工业出版社，1991:134-142.

[15] Kershaw D J.A contribution to performance prediction for probabilistic data association tracking filters [J]. IEEE Transactions on Aerospace and Electronic Systems, 1996, 32(3): 1143-1148.

[16] Wang J T, Qin Y L, Wang H Q. Dynamic waveform selection for maneuvering target tracking in clutter[J]. IET Radar, Sonar & Navigation, 2013, 7(7): 815-825.

[17] 陈伯孝,等. 现代雷达系统分析与设计[M]. 西安：西安电子科技大学出版社，2012:382-389.

WaveformSelf-AdaptionDataAssociationAlgorithmforCognitiveRadarTracking

WANG Shu-liang1, BI Da-ping1,2, RUAN Huai-lin1

(1. Institute of Electronic Contermeasure, National University of Defence Technology, Hefei 230037, China; 2. Key Laboratory of Electronic Restriction, Hefei 230037, China)

For the multiple cross-maneuvering targets tracking in the background of clutter, a waveform self-Adaption data association algorithm for cognitive radar tracking is proposed. This algorithm chooses the range-velocity-bearing as the measurement, and adjusts the waveform parameters to vary the error covariance of the measurement dynamically. Firstly, an optimization probability data association algorithm (OPDA) is given based on the information fusion theory. This algorithm fuses the target position characteristics and motion characteristics to classify the public measurement in the cross area, and makes the multiple cross-maneuvering targets tracking problem into the multiple single-maneuvering target tracking problem. Secondly, the Riccati equation is used to estimate the filtering covariance for the updated target track, and the next waveform is chosen adaptively to improve the tracking performance according to the criterion function of the waveform selection. Simulation results show that this algorithm enhances the environment adaptability of the PDA algorithm, and has superiority than the algorithm without waveform self-adaption.

Cognitive radar; Optimization probability data association (OPDA); Maneuvering target tracking; Waveform self-adaption

2017- 07- 07;

2017- 10- 09

国家自然科学基金(61671453)；安徽省自然科学基金(1608085MF123)

TN953

A

1000-1328(2017)12- 1331- 08

10.3873/j.issn.1000- 1328.2017.12.010

王树亮(1984-)，男，博士研究生，主要研究方向为认知雷达，目标跟踪理论，信号与信息处理技术等。

通信地址：安徽省合肥市黄山路460号博士生队

电话：15156061990

E-mail：wangshuliang211@sina.com